蒸汽发生器传热管一、二次侧耦合换热及管外过冷沸腾数值研究

王成龙，丛腾龙，王泽勇，田文喜，秋穗正，苏光辉，安洪振

(1.西安交通大学 能源与动力工程学院，陕西 西安 710049；2.环境保护部 核与辐射安全中心，北京 100082)

在蒸汽发生器运行过程中，二次侧常伴有复杂的两相流动，会明显改变工质流动和传热特性，对蒸汽发生器的安全性与可靠性造成很大影响。近年来，蒸汽发生器二次侧两相流动沸腾现象研究备受关注。

目前，对蒸汽发生器二次侧流动沸腾的研究大多基于实验，所得实验关联式的局限性较大。也有研究者采用数值模拟方法对蒸汽发生器二次侧流动沸腾进行了研究，大多采用RETRAN、RELAP5和THERMIT等系统程序，但这些程序基本采用一维或简化多维模型，并不能提供蒸汽发生器二次侧的局部流场信息。鉴于此，本工作应用大型商用CFD软件ANSYS CFX 12.0，采用两流体欧拉数学模型并结合Kurual等[1]提出的RPI壁面沸腾模型，对蒸汽发生器二次侧带梅花孔板的两相流动进行模拟，并与一次侧、管壁进行耦合传热计算。

1 数学物理模型

过冷沸腾的多维数值分析计算常采用两流体欧拉数学模型进行，其对气相和液相分别求解一套质量、动量、能量守恒方程，同时考虑气液两相间的传热、传质和动量交换过程。

1.1 两流体欧拉数学模型

质量守恒方程：

ρα·(rαραUα

(1)

动量守恒方程：

ραUα·(rα(ραUα⊗Uα))=

(2)

能量守恒方程：

ραhα·(rα(ραUαhα-λα

(3)

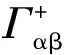
1.2 相间动量交换模型

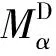
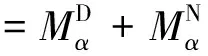
(4)

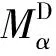
(5)

式中：db为气泡平均直径，m；拽力系数CD取决于气泡雷诺数Reb，本文采用Ishii-Zuber关系式[2]计算。

(6)

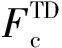
1.3 相间热量传输模型

相间传热采用双热阻模型，用界面传热系数来描述，习惯上采用无量纲努赛尔数Nu表示传热系数。在液相侧，采用Ranz-Marshall经验关系式[4]计算努赛尔数：

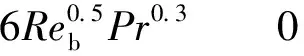
(7)

在气相侧，采用零热阻模型，其换热系数hα为无穷大，等效于交界面温度，等于气相饱和温度。

1.4 相间质量传输模型和RPI壁面沸腾模型

相间质量传输采用热相变模型，而在壁面上的沸腾现象采用RPI壁面沸腾模型进行模拟计算。RPI壁面沸腾模型主要包括两部分：壁面热流密度分配模型和辅助模型。

1) 壁面热流密度分配模型

Judd等[5]的研究结果表明：过冷沸腾时，壁面上的热流密度qw分为3部分：液体单相对流换热带走的热流密度qc，液相蒸发产生气泡时带走的潜热热流密度qe以及淬灭热流密度qq。

qw=qc+qe+qq

(8)

qc的计算公式为：

qc=hcA1(Tw-Tf)

(9)

式中：hc为单相对流换热系数；A1为壁面上液相所占面积；Tw为壁面温度；Tf为液相温度。

qe表示为：

πdbwρgnfhfg/6

(10)

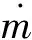
qq采用Mikic等[6]提出的关系式进行计算：

(11)

式中：A2为壁面上气相所占面积份额，A2=1-A1；τw为气泡等待时间；cpf为液相比定压热容。

2) 辅助模型

气泡成核密度n采用Lemmert-Chawla经验关系式[7]进行计算：

n=[210(Tw-Tsat)]1.805

(12)

式中，Tsat为相应压力下的饱和温度

气泡脱离直径dbw采用Tolubinski关系式[8]进行求解：

(13)

式中：dref为参考气泡直径，dref=0.6 mm；dmax为最大气泡直径，dmax=1.4 mm；ΔTref为参考温差，ΔTref=45 K；ΔTsub为近壁面过冷度。

气泡脱离频率f采用Cole关系式[9]计算：

(14)

式中：g为重力加速度；系数CD近似等于1。

气泡等待时间τw采用Tolubinski关系式[8]进行求解：

τw=0.8/f

(15)

气泡平均直径db采用Anglart线性关系式[10]进行计算：

(16)

式中，d0和d1分别为参考过冷度θ0和θ1下的参考气泡直径。

1.5 湍流模型

由于梅花孔板附近有一部分流动为层流，在这部分区域采用k-ε模型将会导致计算发散，因此对于液相采用适应性良好的SST模型，而气相采用弥散相零方程模型。

2 网格划分及边界条件

本文所选取的计算区域为带有支撑板的蒸汽发生器传热管束，包括一次侧、管壁及二次侧。支撑板为三叶梅花孔结构，管束排列为三角形。计算区域示意图如图1所示。高温的一次侧流体从底端流入，将热量传递给管壁，二次侧流体从底端向上流经梅花孔板，最终在一未知高度处发生过冷沸腾。网格划分如图2所示，网格质量大于0.5。

网格进口边界条件为速度进口边界条件，出口边界条件为压力出口。一次侧壁面边界条件设置为无滑移壁面。二次侧壁面边界条件(包括加热壁面和梅花孔板)，对液相设置为无滑移壁面边界条件，对气相设置为滑移壁面边界条件。对于管壁，为便于收敛，底面设置为二次侧进口温度，顶面设置为绝热壁面。其他边界设置为对称边界条件。一次侧与壁面的网格连接方式为GGI模式，二次侧与壁面的网格连接方式为1∶1模式。

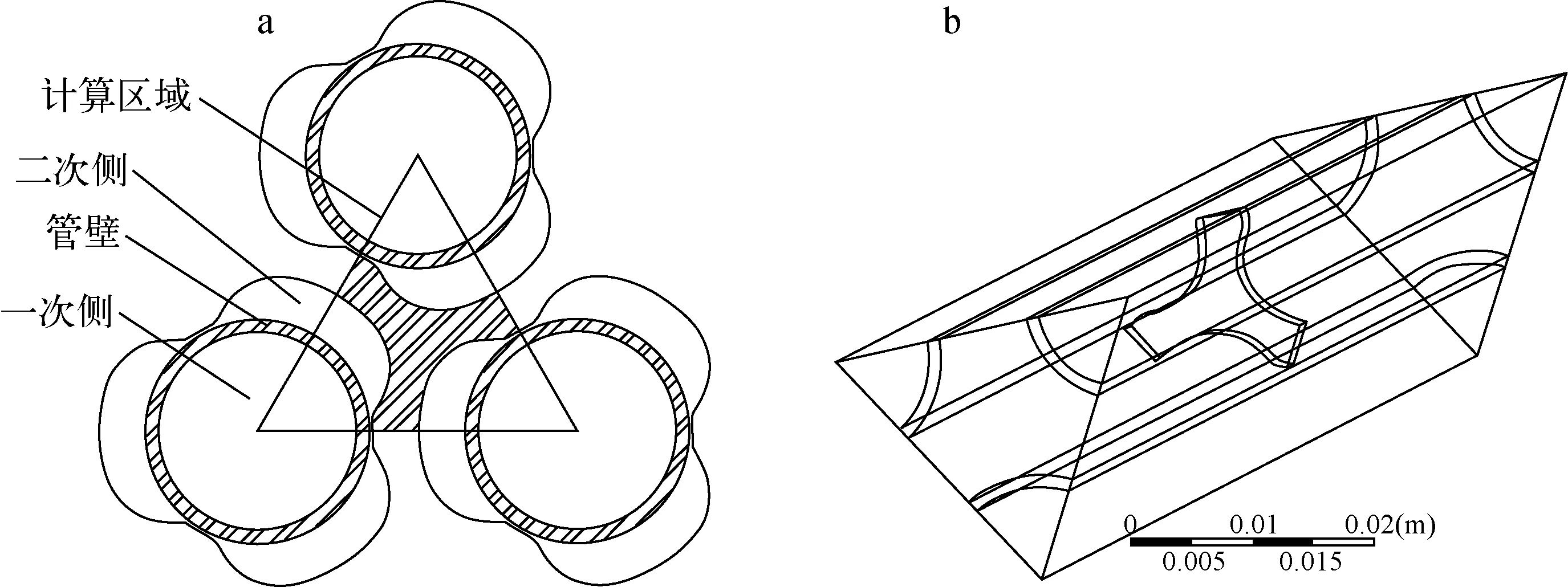
a——支撑板梅花孔结构示意图；b——传热管束三维结构示意图

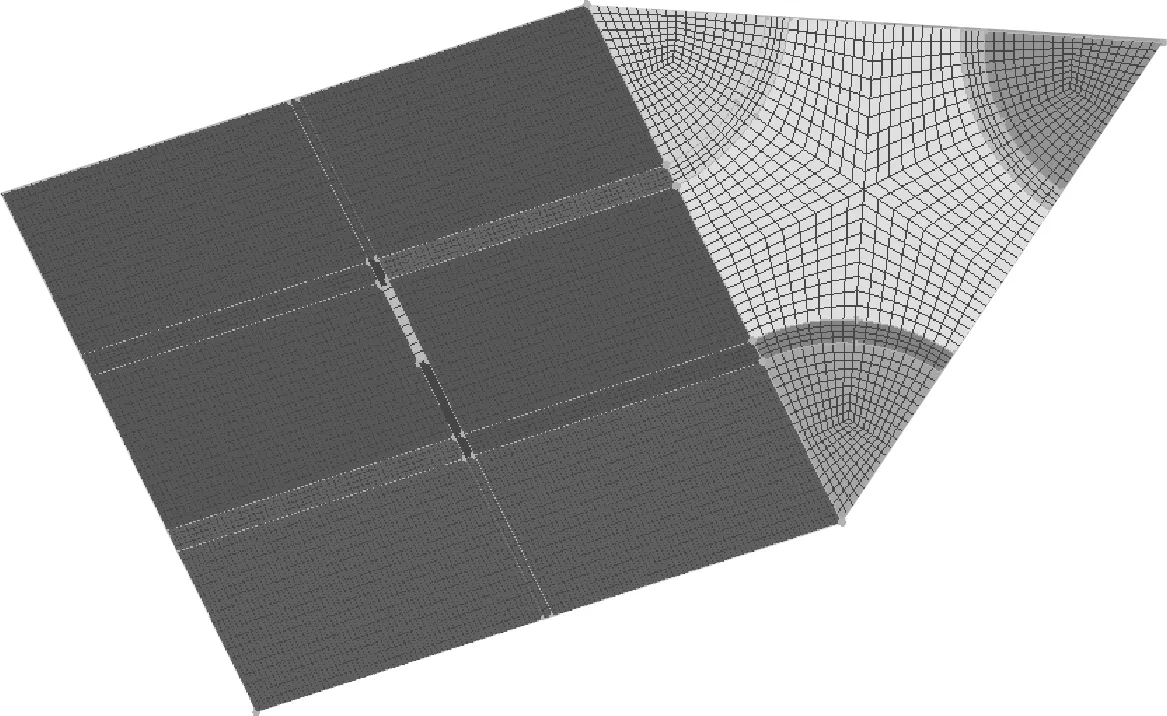
图2 蒸汽发生器传热管束网格划分示意图

3 结果分析及模型验证

3.1 模型验证及网格敏感性分析

本文采用Bartolomej等[11]做的圆管内过冷沸腾实验来验证模型的适用性和准确性。实验圆管长2 m，内径15.4 mm，壁面热流密度5.7×105W/m2，进口质量流量900.0 kg/(s·m2)，压力4.5 MPa，进口过冷度58.2 K，具体几何结构如图3所示。计算结果与实验值的比较如图4所示。图4结果表明，本模型对过冷沸腾的模拟与实验符合较好，其最大相对误差为3.2%，可认为RPI壁面沸腾模型能较好地模拟过冷沸腾现象。

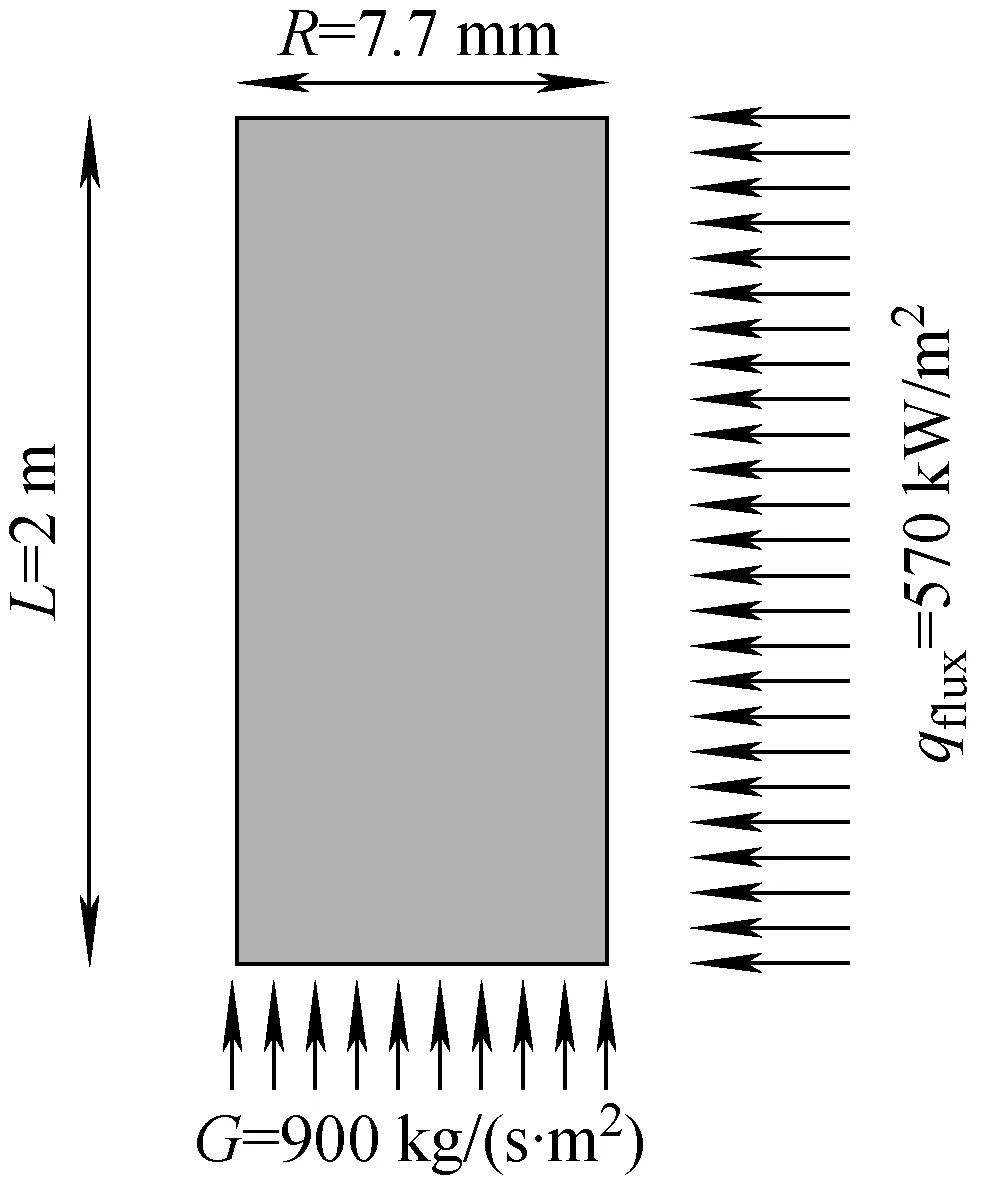
图3 标准题几何模型

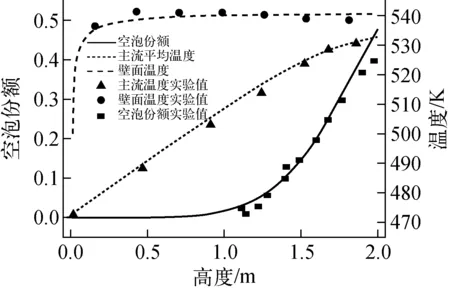
图4 计算结果与实验值比较

为验证网格的独立解，分别对3套网格进行了计算，计算结果列于表1。可看出，随着网格数量的增加，二次侧出口空泡份额和出口温度趋于定值，从而验证了网格的独立解。本次计算中采用第2套网格(1 118 040)进行计算。

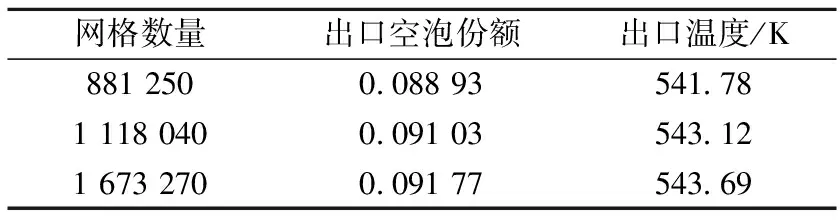
表1 网格敏感性分析

3.2 结果分析

计算工况列于表2。管壁及一、二次侧工质的物性由查表所得。

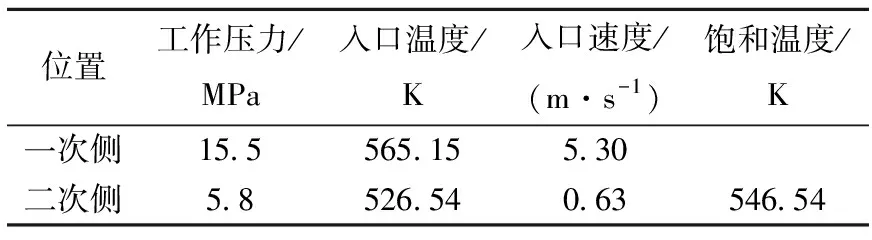
表2 计算工况

图5为二次侧流体流线分布。由于二次侧流体通过梅花孔板时，流通截面突缩，导致流体在此突然加速，最大流速为1.57 m/s。梅花孔处由于流通面积逐渐缩小及其独特的结构，导致流体在流经梅花孔前后产生逆时针旋转流动，如图5b所示。同时还可看出，在梅花孔板窄缝区，由于流体受到两侧壁面(管壁和孔板壁面)摩擦力的作用，其流动速度非常低，为0.004 m/s。

传热管束对称面处一、二次侧流体温度及其梅花孔板局部温度分布如图6所示。由图6a可见，一次侧高温流体由进口流入，不断将热量传入管壁，管壁将热量传递给二次侧流体，最终导致一次侧流体温度降低，其出口平均温度为563.47 K。二次侧流体随热量的不断导入，其温度逐渐上升，出口平均温度为543.11 K。由图6b可见，由于二次侧流体流过梅花孔板处产生逆时针涡旋，其出口处的温度分布不再对称，区域A处的温度略高，而区域B处的略低。由于一、二次侧的耦合效应，一次侧温度也呈现不均匀分布，A侧的换热系数高导致一次侧温度下降较大，而B处的换热系数低导致一次侧温度下降较少。由图6c、d可见，梅花孔板窄缝区的流速很低，导致流体与壁面的换热由原来的对流换热方式转变为以导热方式为主的换热，此处热量聚集导致温度出现局部最大，为552.37 K，超过二次侧流体饱和温度546.54 K，因此，此处很容易发生液相干涸，导致临界热流密度的发生。其他区域的换热以对流换热方式为主，靠近壁面的温度较高，而中心区域的温度较低，如图6d所示。

a——二次侧整体流速分布；b——二次侧流速俯视图

a——一、二次侧温度分布；b——一、二次侧出口温度分布；c——梅花孔板侧面温度分布；d——梅花孔板y=0截面处温度分布

蒸汽发生器二次侧对称面及梅花孔板局部空泡份额分布示于图7。由图7a可见，二次侧流体在离进口约0.23 m处发生过冷沸腾，随着热量的不断导入，截面平均空泡份额逐渐增大，而壁面温度却增加缓慢，约为552.12 K。由于流体逆时针旋转，导致壁面热流密度分布不均，从而造成截面空泡份额分布不均(图7b)。由图7b可见，A区域的平均空泡份额明显大于B区域的，出口平均空泡份额为0.091。由图7c可见，流体流经梅花孔板前时近壁面处空泡份额明显大于流经梅花孔板之后，这是由于梅花孔的结构使液相和气相发生强烈搅混，使得气泡在过冷液相中冷凝的概率变大，最终导致近壁面空泡份额下降。而在孔板窄缝区，由于此处液体的流速极慢，导致此处液相干涸，空泡份额存在一局部峰值，约为0.19。图7d～f示出流体流过梅花孔板不同位置截面处的空泡份额分布，可看出，流体从流进梅花孔板到流出梅花孔板，其截面平均空泡份额依次增大。在截面y=7 mm处存在梅花孔板窄缝区域，存在空泡份额峰值。

a——二次侧空泡份额分布；b——二次侧出口处空泡份额分布；c——梅花孔板处空泡份额分布；d——梅花孔板y=-7 mm处空泡份额分布；e——梅花孔板y=0 mm处空泡份额分布；f——梅花孔板y=7 mm处空泡份额分布

图8 不同高度处截面平均空泡份额分布

图8示出不同高度处截面平均空泡份额分布。由图8可看出，流体流经梅花孔板之前，截面平均空泡份额很低。这时主要为单相液体流动，其壁面上的换热以对流换热为主，而淬灭换热和沸腾换热所占份额很小。流体刚流入梅花孔板，空泡份额降低，这是因为此处液相和气相发生了强烈搅混。随后，空泡份额迅速上升达到0.023，而在孔板出口处空泡份额再次突降，这由流通面积突扩及出口处气液两相的强力搅混两方面因素造成。之后，由于热量不断导入，截面平均空泡份额迅速增加，达到0.091。

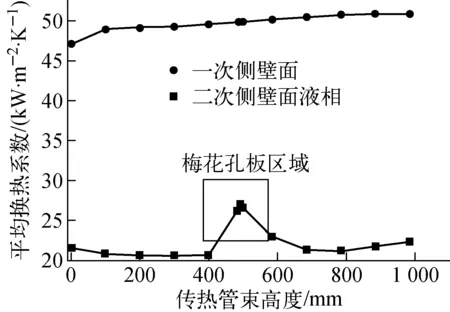
图9 流体壁面平均换热系数随高度的变化

图9示出一、二次侧流体壁面平均换热系数随高度的变化。由图9可看出，一次侧的换热系数随着高度的增加而增大，在出口处达到最大(50 843.90 W/(m2·K))，梅花孔板的存在并未对一次侧换热系数造成影响。二次侧换热系数的变化较为复杂，流体换热系数刚开始随着高度的增加而减小，这主要是由于此时流体流动主要为单相液体流动，进口处温差(主流与壁面)较大，从而导致较高的壁面热流密度，造成较大的换热系数。流体流过梅花孔板处，传热系数突然上升，达到最大值(27 057.70 W/(m2·K))。这主要是由两方面因素造成的：一是截面积的突缩导致流速突然增加，使得对流换热效应大幅增强；二是由于此处的过冷沸腾相对剧烈，增强了换热。此后，壁面换热系数随着高度的增加先有所减小，后逐渐增大。

表3列出蒸汽发生器一、二次侧耦合传热过冷沸腾关键参数的分析结果。

表3 过冷沸腾的分析结果

4 结论

1) 采用RPI壁面沸腾模型对蒸汽发生器二次侧进行过冷沸腾模拟，准确预测了沸腾起始点的位置，在离进口约0.23 m处。利用该模型计算的结果与Bartolomej等[11]的实验结果进行对比，符合良好。

2) 梅花孔板的存在使二次侧流体发生了逆时针涡旋，最终导致一次侧、二次侧的流场、温度场和空泡份额分布不均匀。

3) 梅花孔板窄缝区使得该处的流速极小，导致液相干涸，空泡份额在此处有一局部峰值，易导致传热恶化，管束损毁。因此，利用CFD对梅花孔板区域进行数值模拟对梅花孔板结构设计具有重要意义。

参考文献：

[1] KURUAL N, PODOWSKI M Z. On the modeling of multidimensional effects in boiling channels[C]∥ANS Proceedings of 27th National Heat Transfer Conference. Minneapolis: [s. n.], 1991.

[2] ISHII M, ZUBER N. Drag coefficient and relative velocity in bubbly, droplet or particulate flows[J]. AIChE J, 1979, 25(5), 843-855.

[3] BURNS A D, FRANK T, HAMILL I, et al. The Favre averaged drag model for turbulent dispersion in Eulerian multi-phase flows[C]∥5th International Conference on Multiphase Flow, ICMF-2004. Yokohama, Japan: [s. n.], 2004.

[4] RANZ W E, MARSHALL W R. Evaporation form drops[J]. Chem Eng Prog, 1952, 48(3): 141-146.

[5] JUDD R L, HWANG K S. A comprehensive model for nucleate pool boiling heat transfer including microlayer evaporation[J]. ASME J Heat Transfer, 1976, 94(4): 623-629.

[6] MIKIC B, ROHSENOW W M. A new correlation of pool-boiling data including the fact of heating surface characteristics[J]. ASME J Heat Transfer, 1969, 91(2): 245-250.

[7] LEMMERT M, CHAWLA J M. Influence of flow velocity on surface boiling heat transfer coefficient[M]∥Heat Transfer and Boiling. American: Academic Press, 1977.

[8] TOLUBINSKI V I, KOSTANCHUK D M. Vapor bubbles growth rate and heat transfer intensity at subcooled water boiling[C]∥4th International Heat Transfer Conference. Paris, France: [s. n.], 1970.

[9] COLE R. A photographic study of pool boiling in the region of CHF[J]. AIChE J, 1960, 6(4): 533-542.

[10] ANGLART H, NYLUND O. CFD application to prediction of void distribution in two-phase bubbly flows in rod boundles[J]. Nucl Eng Des, 1996, 163(1-2): 81-98.

[11] BARTOLOMEJ G, BRANTOV V, MOLOCHNIKOV Y S, et al. An experimental investigation of true volumetric vapour content with subcooled boiling in tubes[J]. Thermal Engineering, 1982, 29(3): 132-135.