结合有向场景运动模式的粒子滤波行人跟踪方法

屈鉴铭,刘志镜,贺文骅

(西安电子科技大学计算机学院, 710071, 西安)

结合有向场景运动模式的粒子滤波行人跟踪方法

屈鉴铭,刘志镜,贺文骅

(西安电子科技大学计算机学院, 710071, 西安)

针对现有行人跟踪算法较少考虑场景运动模式信息的问题,建立一种面向有向场景运动模式的在线学习模型以描述区域行人的共有运动特性,并以此提出了一种新型的粒子滤波行人跟踪算法。通过对行人运动特性的选择性在线统计,探索在非高密度行人跟踪问题中场景模式信息和运动历史信息的运用方式。模型由一个表征行人运动状态相空间局域运动特性的二阶直方图矩阵来描述,并根据每个跟踪单元的加权投票实施更新。通过修正粒子转移后似然概率分布,该算法能够加速粒子向真实的后验分布收敛。通过对两个不同特点的公共数据集视频中的行人进行跟踪实验并与标准的粒子滤波算法结果比较,该算法的平均跟踪误差均低于标准粒子滤波平均跟踪误差的40%,且其运算速度可达6～15帧/s,满足近实时应用帧率。

有向场景运动模式;粒子滤波;行人跟踪

行人跟踪是计算机视觉的核心热点课题之一,广泛地应用于智能交通、人机交互、公共安全及国防建设等诸多领域。行人跟踪的关键技术之一是如何选取最有效的迭代滤波算法解决状态的估计问题。早期广为采用的卡尔曼滤波以及其后提出的扩展卡尔曼滤波和无味卡尔曼滤波等算法均是线性动态系统的最优极小方差估计。这些算法虽然能够较好地应用于具有高斯噪声信号系统,但却无法适用于非线性、非高斯动态系统。另一种称作粒子滤波(particle filter, PF)的贯序估计算法能够通过对从当前系统状态分布采样的一群粒子实施加权获取系统后验概率密度分布的近似。因其采用的蒙特卡罗统计方法能够避免递推贝叶斯估计中的高阶积分运算,故更宜解决非线性、非高斯动态系统状态的估计问题。然而,标准粒子滤波采用先验概率分布作为重要性密度函数(importance density function, IDF),当IDF与后验概率分布函数偏差过大时,会导致粒子退化现象的发生。正则化粒子滤波(regularized particle filter, RPF)[1]和马尔可夫链蒙特卡罗(Markov chain Monte Carlo, MCMC)粒子滤波[2]等改进算法采用粒子重采样策略来缓解和克服粒子退化问题。RPF选择从连续概率分布而不是离散分布中采样以减少粒子的多样性衰退,但其具有在高维状态空间中难以实现粒子正则化这一局限性,而MCMC技术基于一个非周期性、不可约马尔可夫链完成粒子重采样,不仅有效地克服了粒子多样性衰退问题,更因为采用了Metropolis-Hastings算法构建转移概率,与其他重采样算法相比也颇具效率优势。因此,本文所述行人跟踪算法在重采样环节采用MCMC技术以达到增强粒子多样性的目的。

反映在行人跟踪领域的另一热点问题,源于对场景空间形态信息的利用程度。众所周知,处于视频监视环境中的行人状态,往往受到场景空间形态的持续影响。因行人运动的意识性兼目的性,通常由场景布局和其他因素引发的诸如运动抑制或运动吸引等影响非常明显,例如一些栏杆、路肩和墙壁等场景元素通常会限制行人的运动,而另一些例如长椅、商场和出入口等场景元素则会给行人带来刺激并产生目的性的运动期望。这种区域内行人运动因场景形态及内部元素作用所表现的规律性称作场景运动模式(scene motion pattern, SMP)。近年来,该领域吸引了计算机视觉领域的广泛关注,为描述群体场景的运动模式,文献[3]提出一种基于结构化场景力学模型,称作地板场理论;文献[4]通过在场景网格空间所建立的一组隐式马尔可夫模型,估计区域运动时空的概率分布,并结合粒子滤波算法对行人实施跟踪;文献[5]针对群体场景的密集光流,使用一种基于无向图的聚类方法;文献[6]则针对群体场景中部分行人的显著性,建立了一种邻近运动一致性的分组模型,再通过混合高斯模型对其聚类以获取相似的运动模式;文献[7]结合马尔可夫随机场的LDA主题模型,对所获取的跟踪单元进行时空关联;文献[8]提出一种基于张量投票的RNMG在线学习算法,通过聚类相似的前景运动,利用贝叶斯估计对目标进行跟踪,因其所提取的运动模式以前景分割为手段,更适用目标较为明显的场景行人跟踪。

综合这一领域的诸多研究,视频行人跟踪亟待解决的问题集中在两方面:一是在非高密度行人监控场景中如何建立有效的场景运动模式模型问题;二是如何利用场景运动模式以改进行人跟踪算法的精度问题。针对以上问题,本文提出一种有向场景运动模式的在线学习模型,并结合MCMC粒子滤波技术,建立一种新型的行人跟踪算法以增强场景模式中局部运动取向信息,通过对行人运动特性的选择性在线统计,探索在非高密度行人跟踪问题中场景模式信息和运动历史信息的运用方式。整个算法的流程如图1所示。

图1 DSMP模型粒子滤波跟踪流程图

1 MCMC粒子滤波

粒子滤波算法的主要思想是通过不断调整从系统状态经验性条件概率分布中采样获取的一群加权随机粒子,实现对系统分布本身的估计。由于行人跟踪问题可视为一个非线性、非高斯随机过程,其动力学空间模型定义为

xk=Φ(xk-1,vk-1),xk∈RNx,vk∈RNv

(1)

zk=Ψ(xk,nk),zk∈RNz,nk∈RNn

(2)

式中:xk和zk分别是系统在k时刻的动力学状态向量和观测向量。本文算法中,xk定义为由二维坐标、速度的方向与大小外加跟踪窗口的宽度和长度所构成的六维状态空间向量,即

xk=[xk,yk,θk,ρk,wk,hk]T

(3)

出现在式(1)的系统噪声向量vk和观测噪声向量nk相互独立,其有界非线性映射Φ和Ψ分别为系统的状态转移函数和观测函数。令p(x0)为系统状态的先验概率,则描述k时刻系统状态的后验概率分布p(x0:k|z1:k)可近似表示为离散形式

(4)

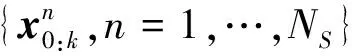
(5)

由此,系统后验概率密度分布进一步表示为

p(x0:k|z1:k)=

(6)

通常使用重要性密度函数作为系统的状态转移概率p(xk|xk-1)。由于每次观测的相互独立性和任一时刻p(zk|z1:k-1)对所有粒子描述的同一性,将式(6)代入式(5),即得到粒子权值的更新公式

(7)

(8)

进行估计。为缓解粒子衰退问题,算法采用前述MCMC重采样技术,通过构造一个极限分布与系统转移概率分布相同的非周期性、不可约马尔可夫链实施粒子采样,并根据Metropolis-Hastings算法计算转换概率。之所以采用MCMC重采样方法,主要鉴于它具有较好的收敛性,且能够快速获取多样化粒子分布并缓解粒子衰退问题等诸多优点。MCMC重采样方法的应用步骤由下述算法给出。

算法1MCMC重采样方法

对于每个粒子n,

产生均匀分布[0,1]随机数,即u～U[0,1]

2 基于有向场景运动模式的行人跟踪

直接通过场景理解获取场景布局信息的方法极为不易,因为正确识别各种场景元素是运用这一方法的前提,但若将场景中每个行人看作独立样本,采用统计方法学习历史跟踪过程中共有的运动规律性,即可在有效避免增加算法复杂性的条件下获取场景运动模式信息。因此,本文提出一种称作有向场景运动模式(directed scene motion pattern, DSMP)的在线学习统计模型以描述区域的共有运动特征。该模型能够有效利用独立行人跟踪的历史信息,并通过对同一区域大量样本在个体上所表现的多态性运动随机状态的学习,统计得出其整体上所表现的稳定的规律性行为,从而决定区域运动的主流模式。

2.1 有向场景运动模式模型

(a)CAVIAR场景图像 (b)CAVIAR 12像素DSMP

(c)PETS09场景图像 (d)PETS09 20像素DSMP

由于给定场景中行人运动的历史信息集中反映于其速度的大小和方向双重因素,DSMP模型选用场景位形空间的二阶方向速率直方图矩阵描述场景空间各个位置不同运动特性发生的概率分布。为使矩阵元素和空间位置一一对应,将整个场景空间分割成边长为SC的均匀正方形网格(i,j),其中i、j分别为网格在x和y方向的离散坐标,每个网格使用一个包含方向和速度大小信息的归一化二维直方图矩阵H描述其所在区域的运动特性。图2直观描述了跟踪场景与该直方图矩阵的关系,其中图2a和图2c分别显示来自CAVIAR和PETS09数据库场景跟踪图像,矩形框表示系统局域状态分布的期望估计,圆点代表粒子当前的局域状态,其半径反映粒子权值;而图2b和图2d分别表示两个数据库场景的DSMP直方图矩阵模型数据,网格线段的亮度表示局域速度大小。每个矩阵元素H(i,j)(d,m)表征在网格点(i,j)处的邻域上发生具有角度范围d和速度范围m内的运动状态的概率。定义k时刻位于(i,j)处,具有系统动力学状态xk的质点的运动特征向量分量yk=[xk,yk,θk,ρk]T,则任一矩阵元素对应表示k时刻位于(i,j)处质点的运动状态特征向量分量的概率密度积分为

H(i,j)(d,m)≅

(9)

考虑到行人运动路径的双向性,DSMP模型的方向维度定义域设置为[0,π)。为保证模型的有向性,定义方向维度的簇宽Ld≤π/2,即模型至少应具备两个角度分量(水平和垂直分量)。同时,速率维度的定义域设置为[Mmin,Mmax],其中Mmin和Mmax是用于过滤噪声和错误跟踪投票的上下阈值。相应的,速率维度的簇宽LM≤(Mmax-Mmin)/2,即模型也应同时具备至少两个速度大小分量(低速和高速分量)。另外,由于行人运动具有主观性和不确定性(即使具有相同的目的,行人的区域运动特性也不尽相同),过多设置分量会导致DSMP模型出现过拟合问题。

注意到尽管对具体跟踪的某一行人来说,其不同空间位置的运动状态具有时间相关性,但对大量描述的行人整体而言,由其统计得到的空间任一位置的区域运动模式一般不具备时间特性。换句话说,尽管DSMP模型的更新需要依赖当前时刻的跟踪结果,模型本身的状态描述却是时间无关的。

2.2 模型更新

为更清晰地理解DSMP的更新机制,需要确切给出有效连续跟踪单元(valid continuous tracklet, VCT)的定义,即在时间间隔δ内目标持续存在条件下,每帧跟踪获取的目标所在空间位置相对于上一帧空间位置在规定阈值范围内的跟踪位移

(10)

阈值设定用于过滤由于位移过大而引发的错误跟踪,而时间间隔δ用于防止因跟踪位移过小而产生的噪声。有效连续跟踪单元是DSMP模型更新的基础和数据来源。跟踪前,描述整个场景区域运动特性的每个二阶网格直方图矩阵均被初始化为二维全零数组。在跟踪过程中,每帧获取的有效连续跟踪片段都会触发对跟踪窗口覆盖区域的直方图的投票。投票使用非加权双线性插值算法,根据有效连续跟踪单元的角度和位移大小选择,针对毗邻的4个直方图矩阵元素实施加权归一化投票。为了过滤跟踪噪声,还需要舍去具有极小位移的跟踪单元。DSMP模型投票更新由下式描述。

(11)

式中:集合Ω包括时刻k场景中所有行人的有效连续跟踪单元;Id,m是跟踪单元vk,δ对模型的相应角度分量d和速度大小分量m的双线性插值系数。整个投票算法如图3所示:图中左侧示意存在有效连续跟踪单元的图像局部,标注纹理的网格均获得该跟踪单元投票;右侧示意某网格直方图方向维和速度维的双线性插值投票。

图3 DSMP模型更新过程示意图

2.3 似然计算

似然概率分布表征时刻k粒子系统状态描述与观测描述的相似程度。为包含行人区域的边缘和颜色分布特征,本文采用颜色直方图和梯度方向直方图的加权组合特征参与似然概率分布计算。记行人初始的归一化特征向量为f0,单个粒子描述的网格区域的归一化组合特征向量为fn,并定义任一向量相对初始向量的特征距离

(12)

式中:b(·)为两特征向量间的巴氏系数。同时引用区域相似性函数

(13)

量度粒子运动状态与其所描述区域运动模式的相似性,则似然概率分布为

(14)

式中:C(·)为归一化系数。利用区域运动模式相似性函数s(·)矫正粒子的似然概率分布,可加速DSMP模型的有效粒子状态向量向真实运动模式收敛,并在目标发生遮挡时促使粒子向区域运动模式接近,从而在目标结束遮挡后使所描述的粒子分布更接近目标运动的真实分布。

3 实验验证与结果分析

实验视频选用CAVIAR行人数据集[9]中的26个视频、共计24 566帧图像序列和PETS09数据集[10]中的14个行人视频、共计6 240帧图像序列进行测试。两个数据集相应的帧率和分辨率分别为25帧/s、384×288像素和7帧/s、768×576像素。所收集的视频序列均由公共场合监视系统录制,其中包含多种行人运动形式,例如正常行走、站立、转身及相互穿插;同时还包含一些群体行为,例如并肩同步、握手、面对面交谈以及撕扯打斗等,因此能够全面地验证跟踪算法的适应性和鲁棒性。

为验证新建算法的有效性,实验在相同视频条件下,将其与标准的粒子滤波算法在同一计算平台的跟踪结果进行对比。针对两种不同分辨率的数据集,DSMP模型分别设置了12和20像素的网格尺度,且有效连续跟踪单元的位移投票阈值均设置为[1,10]。为保证可比性,其余所有参数例如粒子数、系统噪声方差、观测噪声方差、似然分布方差、状态向量阈值等尽可能选取一致。由于测试视频均已标注Ground Truth,跟踪误差可由其标注中心与估计位置中心的欧氏距离计算得出。两种算法对部分行人跟踪测试中跟踪误差ε和平均跟踪误差εavg随帧数f变化的统计结果由图4给出。

实验对比发现,两种算法在程序运行初期ε相当,然而经过一段时间的模型学习后,DSMP粒子滤波算法与传统算法相比逐渐显示出明显的跟踪精度优势,即其平均跟踪误差εavg逐渐减小到更低的水平。统计显示,标准粒子滤波算法经CAVIAR与PETS09视频分别测试的εavg为69.45和275.02像素。相比之下,本文所述算法对于两个数据库视频的测试εavg分别为26.65和83.31像素。由此看出,与标准PF算法相比,基于DSMP的PF行人跟踪算法能够维持更低的平均误差水平,从而具有更为精确的跟踪精度。

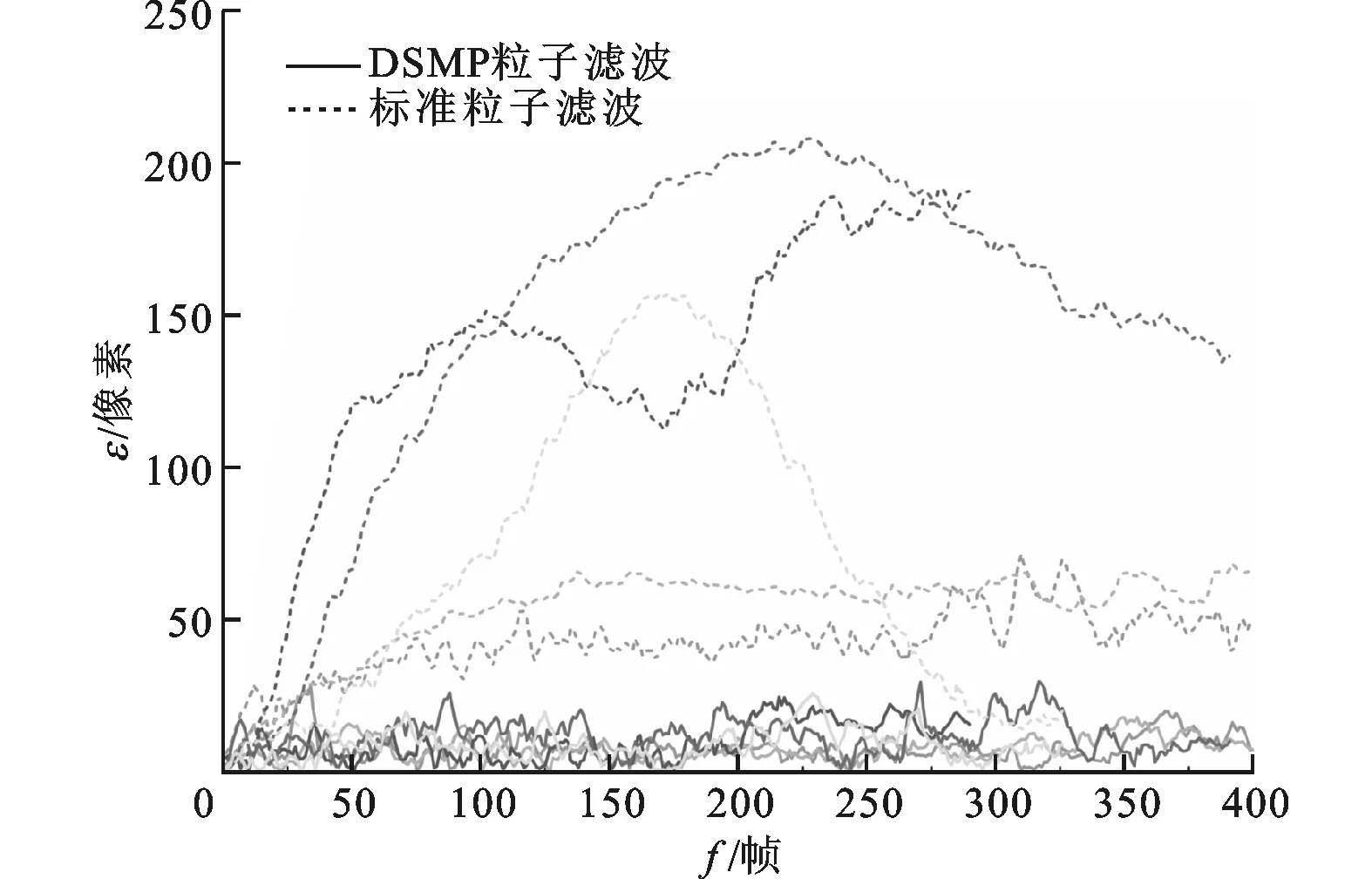
(a)跟踪误差ε比较

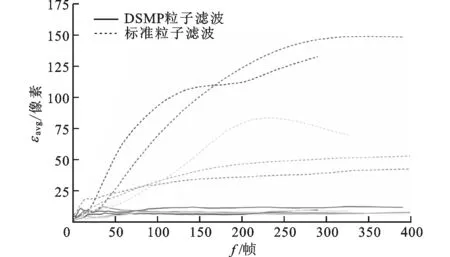
(b)平均跟踪误差εavg比较

实验结果还显示,本文算法对一些行人的跟踪误差明显高于其他行人。经分析,个别行人ε增大的可能原因是跟踪过程行人受到长时间的遮挡、与其他行人过多的拥挤或轨迹交叉等因素影响所导致。由于包含更多群体行为,这种现象在PETS09测试视频运行中尤其突出,甚至包含少量的跟踪失败算例。此外,两种数据库视频的不同分辨率也是可能造成这种现象的原因。

此外,实验还对本文算法在不同DSMP模型分量划分条件下的结果进行测试对比。为增强实验结果的稳定性和可信度,选取测试视频所包含的行人运动相对稳定平缓,发生遮挡、轨迹交错以及拥挤的现象也较少。实验在选取DSMP直方图方向变量簇宽分别为π/2、π/4和π/8以及速度簇宽分别为4、8和10像素/s条件下,将部分视频序列的平均跟踪误差结果记录见表1。比较发现,平均跟踪误差随方向簇宽的增大反映出明显减小趋势,而速度簇宽的改变对评价跟踪误差影响不甚明显。测试还显示,当方向簇宽较大时,误差稳定性略显不佳。因此,本文建议使用π/8的方向簇宽并同时设置4像素/s或8像素/s的速度簇宽以适当降低算法的计算量及所需存储空间。

表1 不同DSMP模型分量划分下的平均跟踪误差比较

算法效率方面,尽管整个测试都在普通双核CPU的个人计算机平台运行且未作特殊的代码优化,DSMP模型的更新帧率仍然达到约80～140帧/s,而总体跟踪算法的帧率也能够基本保持6～15帧/s。若提升硬件性能,采用并行或GPU计算,DSMP粒子滤波跟踪算法的执行效率还会得到进一步提升。

4 结 论

在公共场合监视视频中,传统的行人跟踪算法均未有效地利用场景运动模式中所包含的先验信息。针对这一问题,本文提出一种结合有向场景运动模式和MCMC粒子滤波的在线学习跟踪算法,用于提高行人跟踪的适应性和鲁棒性。实验结果表明,在近实时的运算速度下,该算法能够加快粒子向真实概率分布收敛,且能够保持更低的跟踪误差,从而获得更高的跟踪精度。下一步工作的重点是使用并行计算进一步提高算法的跟踪精度和效率。

[1] MUSSO C, OUDJANE N, GLAND F L. Improving regularised particle filters [M]∥ Sequential Monte Carlo Methods in Practice. New York, USA: Springer, 2001: 247-271.

[2] GILKS W R, BERZUINI C. Following a moving target: Monte Carlo inference for dynamic Bayesian models [J]. Journal of the Royal Statistical Society: Series B Statistical Methodology, 2001, 63(1): 127-146.

[3] ALI S, SHAH M. Floor fields for tracking in high density crowd scenes [M]∥ Computer Vision-ECCV. Berlin, Germany: Springer-Verlag, 2008: 1-14.

[4] KRATZ L, NISHINO K. Tracking with local spatio-temporal motion patterns in extremely crowded scenes [C]∥Proceedings of the 2010IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ, USA: IEEE, 2010: 693-700.

[5] XU Feiming, LU Tong, WU Yirui. Robust object tracking using motion context in crowded scenes [M]∥ Advances in Multimedia Information Processing. Cham, Switzerland: Springer International Publishing, 2013: 550-560.

[6] IDREES H, WARNER N, SHAH M. Tracking in dense crowds using prominence and neighborhood motion concurrence [J]. Image and Vision Computing, 2014, 32(1): 14-26.

[7] ZHOU Bolei, WANG Xiaogang, TANG Xiaoou. Random field topic model for semantic region analysis in crowded scenes from tracklets [C]∥Proceedings of the 2011IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ, USA: IEEE, 2011: 3441-3448.

[8] ZHAO X, MEDIONI G. Robust unsupervised motion pattern inference from video and applications [C]∥Proceedings of the 2011IEEE International Conference on Computer Vision. Piscataway, NJ, USA: IEEE, 2011: 715-722.

[9] CAVIAR Project. CAVIAR database [DB/OL]. (2005-09-30)[2014-06-01]. http:∥homepages.inf.ed.ac.uk/rbf/CAVIAR/.

[10]UK EPSRC REASON Project. PETS2009 DataSet[DB/OL]. (2009-10-07)[2014-06-01]. http:∥pets2009.net/.

(编辑 武红江)

PedestrianTrackingUsingDirectedSceneMotionPatternandParticleFilter

QU Jianming,LIU Zhijing,HE Wenhua

(School of Computer Science and Technology, Xidian University, Xi’an 710071, China)

An online learning model oriented to directed scene motion patterns and based on particle filter is proposed to get over the problem that existing pedestrian tracking algorisms have little consideration on the scene motion patterns, to process the priori scene information and to improve the precision of pedestrian tracking. The model describes the local motion characteristic in phase space of the system state vector using a direction-speed motion histogram matrix, and is updated according to weighted voting of each track unit. The particle filter can accelerate the particles evolution to the true posterior distribution through modifying likelihood probability distribution of particle transfer. Experimental results on two pedestrian data sets with different characteristic forms and comparisons with the standard particle filter algorithm show that the average tracking error of the proposed approach is 40% lower than that of the standard particle filter algorithm, while its computation speed approaches the range of 6 to 15 frames a second, and that the proposed approach completely meets the conditions of real-time application.

directed scene motion pattern; particle filter; pedestrian tracking

2014-06-16。

屈鉴铭(1985—),男,博士生;刘志镜(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(61173091)。

时间:2014-11-27

10.7652/xjtuxb201412012

TN911.73

:A

:0253-987X(2014)12-0074-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20141127.1818.001.html