心肌细胞钾通道调控早期后除极的动力学机制

张虹,赵丹,李蕊娟

(西安交通大学电气工程学院, 710049, 西安)

心肌细胞钾通道调控早期后除极的动力学机制

张虹,赵丹,李蕊娟

(西安交通大学电气工程学院, 710049, 西安)

针对心肌细胞动作电位复极期振荡的早期后除极(EAD)现象,研究了细胞模型Hopf分岔和EADs的关系以及钾离子通道的作用。在LR91模型中剔除快钠离子电流并引入控制钙和钾离子通道时常数的控制因子形成子系统模型,分离出模型中不同时间尺度的变量,将跨膜电势、钙离子通道激活及失活门控变量视为快变量构成三变量快子系统,慢变量钾离子通道门控参数视为其分岔参数分析膜电位与快子系统稳定性的关系。计算机仿真结果表明,随着钾离子通道门控变量时常数的增大,膜电位越来越接近快子系统的吸引域和Hopf分岔点。当时常数增大到6倍时动作电位时程延长至1 060 ms并开始出现膜电位的振荡,时常数增大到15倍时电位振荡个数增加至15,说明快子系统的Hopf分岔导致了钾通道门控作用下EAD的诱发。

钾离子通道;早期后除极;Hopf分岔;动作电位;计算机仿真

室颤是心源性猝死的主要原因之一。心室肌电折返以及早期后除极(EAD)引起的触发激动是诱发室颤的两种主要因素,其中EAD是指在心肌细胞复极化阶段,由于病理或药物毒副作用,膜电位停滞于平台期并发生多次振荡的现象。若EAD引起的振荡幅度达到邻近细胞的阈电位,可引起细胞产生动作电位并通过触发激动导致室性心律失常。临床研究发现,高危性的尖端扭转性室性心动过速很可能由EAD诱发[1]。因此,研究EAD的产生机制和条件一直是人们关注的一个重要问题。

长期的研究发现,细胞膜内向型电流的增加或外向型电流的减小往往伴随着EAD的产生[2-3]。但是,电流的这种改变并不一定都能够成功地诱导出EAD[4],尽管动作电位时程(APD)的延长易于诱发EAD现象[5],但其内在机制目前尚不完全明确。钾离子通道作为动作电位复极化阶段的主要参与者,其行为会影响APD,进而影响细胞模型稳定性和EAD的产生,因此钾离子通道调控行为与EAD之间的关系值得深入探讨。近年的研究提出EAD的产生并非随机,而是存在动力学混沌现象[6],该发现改变了人们长期以来认为的EAD是由细胞离子通道的随机波动引起的无规律性膜振荡的观点。

基于细胞离子通道的数学模型一直是心脏电生理定量研究的基础。然而,该类模型往往采用高维微分方程组的数学表述形式,具有多变量强耦合非线性特点,这给动力学分析带来了一定困难[7]。由于不同细胞膜电流的激活和失活往往具有不同的时间尺度,因此本文通过在原有模型上构建快子系统,使用局部线性化的动力学方法分析了单细胞模型的稳定性,研究了系统Hopf分岔和EADs的关系,以及钾离子通道在其中的作用。

1 方 法

1.1 子系统模型的构建

本文在Luo和Rudy(LR91)心室肌模型[8]的基础上构建了子系统模型。由于钠离子通道的激活主要发生在动作电位除极时相,失活速率非常快,因此钠离子电流在复极阶段几乎为零,对复极平台期的影响微乎其微,而EADs主要发生在平台期,所以本文在原有模型中移出钠离子电流,剔除无关量,构成的离子通道模型[9]如下

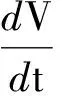
(1)

式中:V为跨膜电势;Cm为跨膜电容;Isti为刺激电流;Isi为L型钙离子电流;IK为时间依赖型钾离子电流;Io为时间无关型钾离子电流。

离子电流受到各自通道门控变量的调节,其中Isi的门控变量为钙离子激活门控变量d和失活门控变量f;IK的门控变量为激活门控变量x。d、f及x的行为可用以下微分形式的通式来描述[10]

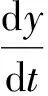
(2)

(3)

(4)

式中:y代表d、f及x中的任意一个门控变量;τy代表d、f及x对应的时常数τd、τf和τx;y∞代表每种时常数的稳态值;αy和βy代表由跨膜电压决定的速率常数。

为了实现对门控变量时常数的调控,分别给τd、τf和τx引入控制因子Cd、Cf和Cx,因此式(2)～(4)中τy所代表的时常数τd在解算时取为Cdτd、τf取为Cfτf、τx取为Cxτx。

文中把去除了钠电流以及引入控制因子后的模型称为子系统模型,该模型剔除了原有模型的钠通道电流,在便于后续分析的同时,又保持了原系统在动作电位平台期的特征。因此,子系统模型可反映原系统在平台期的行为。

上述模型的解算采用欧拉法,其中Cm=104μF/m2,Gsi=0.15,Esi=80 mV,EK=-77 mV。外部刺激电流脉宽取为2 ms,幅值为3×105μA/m2。

1.2 快子系统模型及其分叉分析

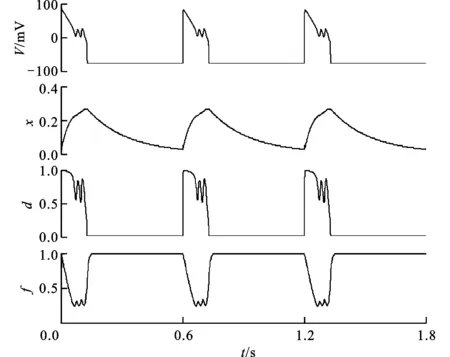
图1 膜电位及门控变量随时间的变化

由于子系统模型中各门控因子的时间尺度不一致,于是形成了快慢效应。文中首先求解式(1)～(4)以确定V、d、f和x的快慢特性。图1给出了Cd=0.2、Cf=1.1、Cx=10时,膜电位以及各门控变量之间的相互关系。由图可知,4个变量中x的振动频率是单一的,而V、d、f振动频率一致且包含有多个频率分量,其基频与x的频率相同。可见,子系统模型参量具有显著的快慢效应,即系统中存在着与变量V、d、f相关的快时间尺度和与变量x相关的慢时间尺度。

根据上述分析,利用快慢动力学方法[11],建立以膜电位V、门控变量d和f为基础的三变量快子系统模型

(5)

并将慢变量的钾离子门控变量x视为快子系统的分岔参数。采用局部线性化方法,得到快子系统的Jacobian矩阵

(6)

式中

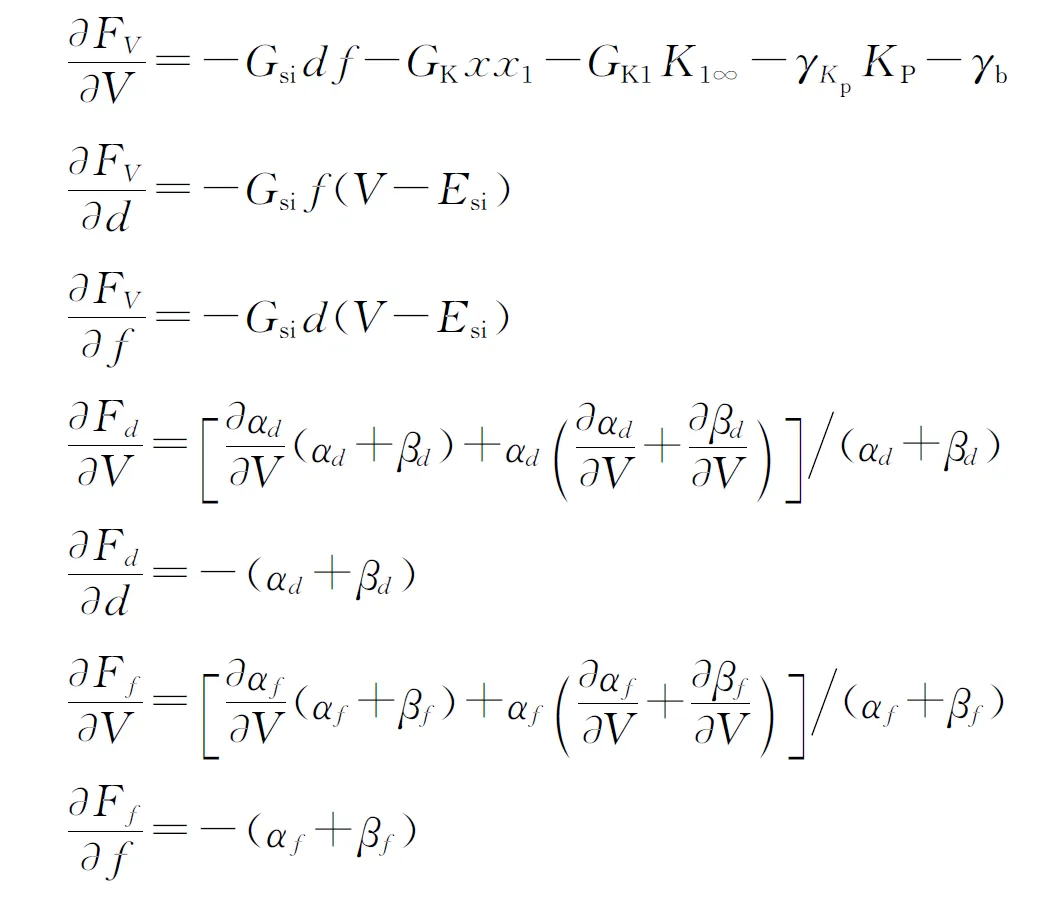
其中

文中利用动力系统数值模拟和分岔分析软件XPPAUT对快子系统进行分析,首先得到快子系统的数值解,获得稳定的平衡点,然后分析分岔参数x变化时系统的稳定性。

2 结果与讨论

2.1 快子系统模型的稳定性

图2给出了以x为分岔参数的三变量快子系统的稳定性情况。点1为端点,其对应的x和V分别为0和-12.54 mV;点3为转折点,x和V分别对应0.709 1和-28.85mV;点2为Hopf分岔点(HB点),其x和V分别对应0.231 7和-16.41 mV。图中实线对应稳定的平衡点,虚线对应不稳定状态,在交界处出现了Hopf分岔点。

图2 快子系统相对于x的稳定性

2.2 钾离子通道门控变量诱发EAD与Hopf分岔的关系

图3为子系统在不同的钾通道门控变量时常数时的膜电位及其与系统稳定性的关系。图3a中,Cx=1时,APD为482 ms,动作电位可正常除极和复极,无平台期电位振荡;Cx=4时,APD延长至683 ms,但仍未出现电位的波动;Cx=10时,APD延长至2 377 ms,并在复极平台期出现了连续7个电位波动,产生EAD现象。可见,随着门控变量时常数的增大,APD显著延长并出现EAD,这与众多实验中观察到的现象一致[12-13]。

为了对比膜电位变化与快子系统稳定性的关系,图3b将上述3种情况下膜电位相对于x的变化图与快子系统以x为分岔参数的稳定性关系图叠加。观察发现:对于出现EAD的情况(Cx=10),当x从0开始略有增加时,膜电位V即迅速地从-80 mV上升到40 mV;达到峰值后,随着x的增加,膜电位趋向快子系统的吸引域,并在Hopf分岔点前与之相交于点A;之后,膜电位围绕着稳定平衡点以欠阻尼方式振荡,振幅逐渐减小,但在经过Hopf分岔点2后出现转折,开始以振幅增大的方式振荡并伴有周期的增加。对于没有出现EADs的情况(Cx=1,4),由于此时钾离子通道门控变量x对应的时常数较小,导致了x的迅速增大,促使子系统远离了快子系统的吸引域,因而没有出现膜电位的波动。以上分析说明,钾通道门控变量对膜电位具有调控作用,但是膜电位是否发生振荡并出现EAD根本上则是由快子系统的Hopf分岔决定的。

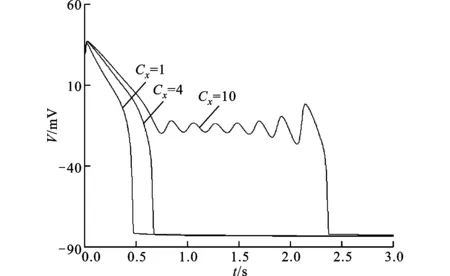
(a)膜电位相对于时间的变化

(b)膜电位相对于x的变化及与快子系统稳定性的对照

为进一步验证上述结果,实验中观察了Cx分别取1到15时膜电位与快子系统分岔间的关系,图4给出了具有代表性的6种情况,其他情况所反映的特征与之完全一致,故未一一给出。由图可见:当Cx从1增至5时未发生EAD,但随着Cx的增大,由于x变化率的减小,使子系统越来越接近快子系统的吸引域和Hopf分岔点;当Cx为6时,在接近Hopf分岔点处开始出现膜振荡;之后随着Cx的继续增加,x快速趋向快子系统的吸引域,并在Hopf分岔点前以欠阻尼方式振荡,过了Hopf分岔点后振幅加强。Cx越大,振荡开始时对应的x值越小,从而使膜电位波动次数增多。图4c和4d的波动个数分别为5和11。

图5给出了APD及膜电位波动个数与Cx的关系。由图可见:当Cx小于5时,APD以较小的斜率从483 ms增加到725ms,此变化范围内无EAD;Cx大于5后,APD增长加快,从Cx等于6时的1 060 ms增大到Cx等于13时的3 627 ms;当Cx大于13.5后,APD大于4 000 ms。在此范围内,伴随着APD的延长,同时产生EAD,膜电位的振荡个数也从1增大到15。

(a)Cx=1,3,5(b)Cx=6

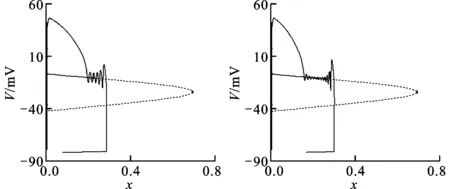
(c)Cx=9 (d)Cx=12

P代表APD;N代表膜电位波动个数

上述实验进一步表明,钾通道门控变量的时常数可影响APD。当时常数大于原有值的6倍以上时,由于子系统的状态趋近于快子系统的吸引域和Hopf分岔点开始出现膜振荡。子系统的状态越趋近吸引域,振荡越明显,振荡波的个数也越多。由此可见,膜电位处于Hopf分岔点附近应是EAD发生的基础。

本文重点研究了钾离子通道对EAD调控的动力学机制。实验中钙离子通道门控时常数的调控因子Cd为0.2,Cf为1.1。当Cd和Cf取其他值时,Hopf分岔点的具体位置和膜电位会有所改变,但两者的相对关系和变化规律仍符合目前的研究结果。

3 结 论

本文利用快慢动力学分析方法从非线性动力学的角度探讨了钾离子通道门控作用下EAD产生的原因,结果表明,钾通道门控变量对膜电位具有调控作用。伴随着时常数的增加,APD延长并开始出现膜电位的振荡,但EAD发生的内在机制却在于快子系统的Hopf分岔行为,膜电位处于分岔点附近是导致EAD发生的基础。钾离子通道通过调节门控变量影响膜电位,当这种影响促使膜电位趋向于分岔点时,为膜电位的振荡创造了条件而导致EAD的发生,因此快子系统的Hopf分岔是钾离子通道门控作用下诱发EAD的主要原因。

[1] 王军奎, 于忠祥,崔长琮.药物致尖端扭转型室性心动过速的发生机制 [J].南方医科大学学报, 2013, 33(7): 1093-1096.

WANG Junkui, YU Zhongxiang, CUI Changcong.Mechanism of drug-induced torsade de pointes: an experimental study in dogs [J].Journal of Southern Medical University, 2013, 33(7): 1093-1096.

[2] ZHAO Zhenghang, WEN Hairuo, FEFELOVA N, et al.Revisiting the ionic mechanisms of early afterdepolarizations in cardiomyocytes: predominant by Ca waves or Ca currents [J].American Journal of Physiology-Heart and Circulatory Physiology, 2012, 302(8): H1636-H1644.

[3] VOLDERS P G, VOS M A, SZABO B, et al.Progress in the understanding of cardiac early afterdepolarizations and torsades de pointes: time to revise current concepts [J].Cardiovascular Research, 2000, 46(3): 376-392.

[4] LI Guirong, LAU C P, DUCHARME A, et al.Transmural action potential and ionic current remodeling in ventricles of failing canine hearts [J].American Journal of Physiology-Heart and Circulatory Physiology, 2002, 283(3): H1031-H1041.

[5] WEISS J N, GARFINKEL A, KARAGUEUZIAN H S, et al.Early afterdepolarizations and cardiac arrhythmias [J].Heart Rhythm, 2010, 7(12): 1891-1899.

[6] QU Zhilin, XIE Laihua, OLCESE R, et al.Early afterdepolarizations in cardiac myocytes: beyond reduced repolarization reserve [J].Cardiovascular Research, 2013, 99(1): 6-15.

[7] 王江, 张骅, 曾启明.肌肉中的HH模型钠离子通道反电势的Hopf分岔分析 [J].系统仿真学报, 2004, 16(10): 2276-2284.

WANG Jiang, ZHANG Hua, ZENG Qiming.Analysis of Hopf bifurcation caused by sodium ions anti-electro-motive in the Hodgkin-Huxley model in muscles [J].Journal of System Simulation, 2004, 16(10): 2276-2284.

[8] LUO C H, RUDY Y.A model of the ventricular cardiac action potential depolarization, repolarization and their interaction [J].Circulation Research, 1991, 68(6): 1501-1526.

[9] TRAN D X, SATO D, YOCHELIS A, et al.Bifurcation and chaos in a model of cardiac early afterdepolarizations [J].Physical Review Letters, 2009, 102(25): 2581031-2581034.

[10]金印彬, 杨琳, 张虹, 等.二维心室肌中动作电位传导的数值算法研究 [J].西安交通大学学报, 2004, 38(8): 851-854.

JIN Yinbin, YANG Lin, ZHANG Hong, et al.Numerical algorithm for conduction of action potential in two dimensional cardiac ventricle tissue [J].Journal of Xi’an Jiaotong University, 2004, 38(8): 851-854.

[11]IZHIKEVICH E M.Neural excitability, spiking and bursting [J].International Journal of Bifurcation and Chaos, 2000, 10(6): 1171-1266.

[12]LI Guoliang, CHENG Gong, WU Jing, et al.Drug-induced long QT syndrome in women [J].Advances Therapy, 2013, 30(9): 793-802.

[13]MARUYAMA M, XIAO Jianmin, ZHOU Qiang, et al.Carvedilol analogue inhibits triggered activities evoked by both early and delayed afterdepolarizations [J].Heart Rhythm, 2013, 10(1): 101-107.

(编辑 赵炜)

DynamicMechanismsofAfterdepolarizationintheEarlyRegulationofCardiacPotassiumChannel

ZHANG Hong,ZHAO Dan,LI Ruijuan

(School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

The relationships between the Hopf bifurcation in the cellular model and the Early Afterdepolarization (EAD) and the function of potassium channel are investigated for the EAD phenomenon of the voltage oscillation during the repolarizing phase of the cardiac action potential.A subsystem model is developed by removing the fast activated sodium current in the LR91 model and introducing control factors for time constants of calcium and potassium channels.Variables with different time scales are separated.A fast subsystem with 3 variables is formed and the variables are voltage, activation and inactivation gating variables of calcium channel.The relationship between the voltage and the steady state of the fast subsystem is analyzed by regarding the gating variable of the potassium channel as a bifurcation parameter.Simulation results show that the voltage approaches the attraction and Hopf bifurcation point more and more as the time constant of potassium channel gating variable increases.The action potential duration (APD) is prolonged to 1 060 ms and the voltage oscillation appears when the time constant is 6 times of its control value.The number of the oscillation waves increases to 15, when the time constant approaches 15times.The results show that the Hopf bifurcation of the fast subsystem results in induction of EAD under the control of the potassium channel.

potassium ionic channel; early afterdepolarization; Hopf bifurcation; action potential; computer simulations

2014-06-03。

张虹(1969—),女,博士,副教授。

国家自然科学基金资助项目(81271661);教育部回国留学基金资助项目(第40批);中央高校基本科研业务费专项资金资助项目(xjj2011087)。

时间:2014-08-13

10.7652/xjtuxb201411016

TP391.9

:A

:0253-987X(2014)11-0092-05

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140813.1008.004.html