认知无线电系统的顽健资源分配算法

徐勇军，赵晓晖

(吉林大学 通信工程学院，吉林 长春 130012)

1 引言

近年来，随着人们生活水平的提高和无线通信业务的迅速发展，频谱资源作为一种珍贵的有限资源变得越来越紧张。由于现有的频谱授权机制采用固定的频谱分配方式，使得频谱利用率低，造成大量的频谱资源浪费，因此，如何提高频谱资源的重复利用率，缓解频谱资源紧张的问题，成为目前无线通信领域亟待解决的问题。认知无线电（cognitive radio）技术[1]正是在这样的情况下应运而生。

传输功率控制是认知无线电资源分配的关键技术。近年来，针对不同的优化指标和约束条件，选择合理的功率分配方式受到学者们的关注[2,3]。虽然这些方法在实现频谱资源分配方面取得了一些研究成果，但没有考虑参数不确定性对系统性能的影响，都假设系统参数能够精确得到。然而，由于信道估计误差、量化误差和时延等影响，很难获得精确的系统参数。因此，在实际通信环境中，基于名义模型的算法可能由于这些不确定性会出现用户的通信中断问题。从而，有必要考虑和研究算法的顽健性。

目前，国内外对认知无线电顽健性方面的研究较少，已存在的工作集中在认知系统顽健波束成形器设计上[4,5]，很少有关于认知无线电顽健控制方面的研究。文献[6]考虑噪声和QoS的时变性，利用顽健帕累托（Pareto）优化方法实现无线蜂窝系统中顽健传输功率最小问题。文献[7]基于有界信道不确定性模型，提出一种顽健功率控制博弈算法实现网络速率最大。虽然上述2种方法是对顽健资源分配问题的初步尝试，但是没有考虑认知场景。近年来，认知无线电系统中参数不确定问题逐渐引起人们的关注[8～10]。文献[8]基于二阶锥规划（SOCP）提出了一种分布式顽健功率控制算法，但只考虑了单用户情景。在多用户环境下，基于正交频分复用（OFDM）技术，文献[9] 提出了顽健迭代注水算法实现用户数据速率最大化。考虑用户信干噪比（SINR）和干扰温度中断概率约束，基于连续几何规划方法，文献[10]研究了网络效用最大化问题。然而，由于不确定性概率分布和统计信息很难得到，因此上述基于概率约束优化模型的算法不易实现。进一步，针对一个认知空间/时分多址（STDMA）网络，考虑最坏SINR和干扰温度约束，文献[11]基于分布式列生成方法实现最小认知链路传输长度。考虑下垫式认知通信环境，信道不确定性定义为估计值和精确值的有界距离，文献[12]提出了一种顽健干扰控制方法实现认知用户吞吐量最大。然而，忽略了每个次用户的QoS需求。文献[13]在文献[12]的基础上，考虑SINR约束，提出了一种分布式顽健功率控制方法。通过辅助变量将原优化问题转换为一个几何规划问题求解，由于没有考虑认知用户直接信道增益和噪声干扰摄动影响，且将效用函数近似处理，并不适用于低SINR情景。

可以发现，目前已有的顽健资源分配算法主要是以多天线系统和最大化吞吐量为优化目标，在单用户场景考虑干扰温度中信道增益的不确定性影响。虽然该类算法能够实现在参数摄动下保证主用户通信质量，由于缺少对SINR的考虑，次用户的通信质量得不到保障。

针对认知无线电系统参数不确定性问题，本文提出了一种顽健资源分配算法。该算法以最小化次用户总的发射功率为目标，考虑次用户发射功率和最小期望SINR约束及主用户干扰温度约束，采用欧几里得球形不确定性描述信道增益不确定性，基于worst-case约束，将顽健功率控制问题转换为一个确定性的资源分配问题，并利用拉格朗日对偶原理及次梯度更新方法求解。该算法可同时保证主用户和次用户的QoS，减小用户之间的信息交换。仿真结果表明所提出的顽健算法以达到次优性能为代价来提高系统的顽健性。

2 系统模型

考虑多用户分布式认知无线电网络，假设系统中有M对认知用户，N对主用户。认知用户和主用户链路集合分别定义为A={1,…,M}和B={1,…,N}，且∀i,j∈A,∀k∈B。其中，i,j表示网络中任意2个不同的认知用户通信链路，k表示网络中任意一个主用户通信链路。假设每条链路有一对收发机，且都为单天线通信。为了在下垫式（underlay）频谱共享方式下保证主用户的QoS，次用户发射功率需要满足如下干扰温度约束：

其中，hki表示链路i上次用户发射机到链路k上主用户接收机间的链路增益；pi为链路i上次用户发射机的发射功率；表示链路k上主用户接收机能忍受的最大干扰功率（干扰温度线）。

链路i上认知用户接收机的信干噪比SINR为

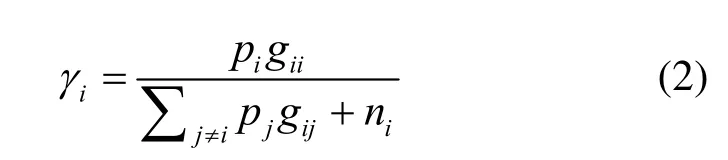
其中，iig为链路i上的直接信道增益；ijg表示链路j上认知用户发射机到链路i上次用户接收机的干扰信道增益；jp为对应链路j上认知用户发射机功率；in表示非认知用户带来的干扰与噪声功率之和，包括背景噪声和网络中所有主用户对链路i上认知用户接收机的干扰。

为了防止网络中其他用户的干扰和环境噪声影响每个认知用户的基本通信要求，每个认知用户接收机端应该满足如下SINR约束

本文优化目标为：最小化总的功率消耗同时满足次用户发射功率不超过最大电池容量（用户最大发射功率），并同时满足约束条件式(1)和式(3)。上述功率优化问题从数学上可以描述为

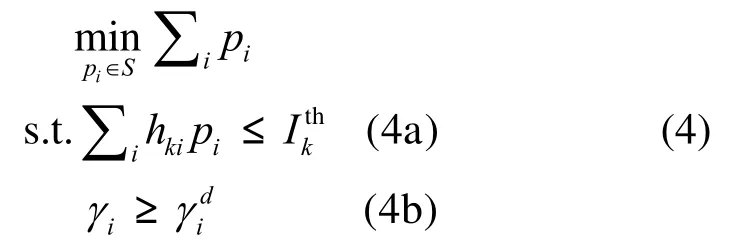
由于实际通信系统中存在量化误差、信道估计误差和延时等因素影响，导致认知用户不可能完全准确知道系统的状态信息。由于无线通信的随机特性，基于名义优化模型的算法[2,3]往往不能满足实际需求，所以需要讨论顽健资源分配问题。

3 顽健功率控制算法

考虑到式(4)中信道增益的不确定性，结合欧几里得球形不确定性描述，讨论了一种分布顽健功率控制算法，解决系统参数摄动的资源分配问题。

将信道增益kih的不确定描述为如下形式的欧几里得球不确定形式。

其中，hℜ代表信道不确定性集合；代表信道实际值；[·]T表示向量或矩阵的转置；表示欧几里得范数；为相应的估计信道增益向量，为球的中心；球的半径大小由δk决定(δk≥0)，描述估计值和实际值之间的偏差程度；半径δk越大代表估计值越不准确，估计误差较大。同时，信道不确定性可表示为其中，为范数有界误差向量，且满足

由不确定信道描述和优化问题式(4)，可得顽健资源分配问题为

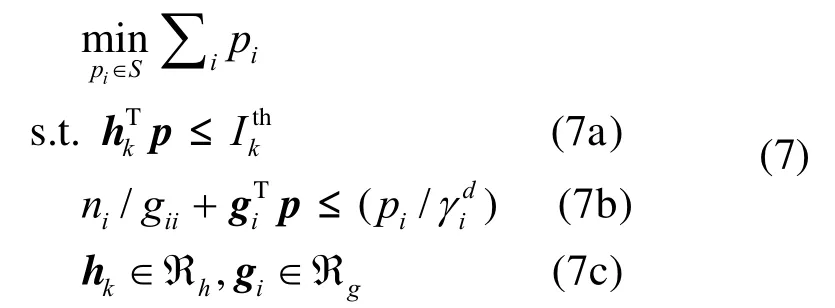
为了获得顽健问题的解析解，需要将问题(7)转换为一个确定性优化问题。考虑最坏约束情况下，干扰信道不确定性可以表示为

同理，不确定性SINR满足

结合式(8)和式(9)，得到如下资源分配问题

问题(10)的拉格朗日函数为

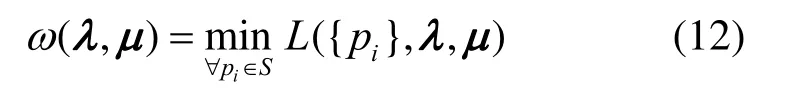
式(12)可以分解为M个独立的问题，每个子问题为每条认知链路i上次用户的资源分配问题

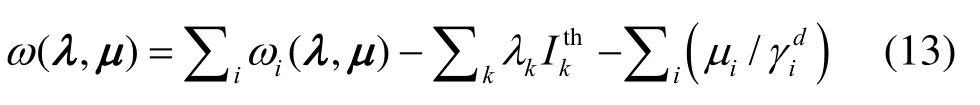
其中，ωi( λ, μ)满足

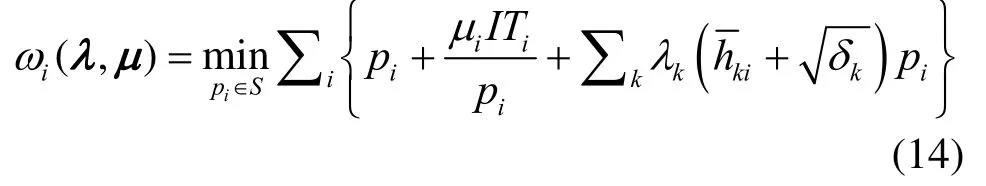
对于任意确定的对偶变量(,)λ μ，式(14)是关于变量ip的一个凸函数。基于KKT条件[14]，最优功率解可表示为

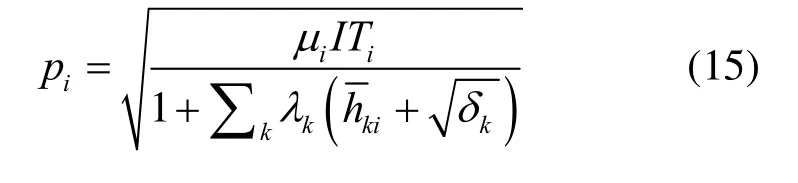
根据次梯度更新算法，得到对偶变量的更新

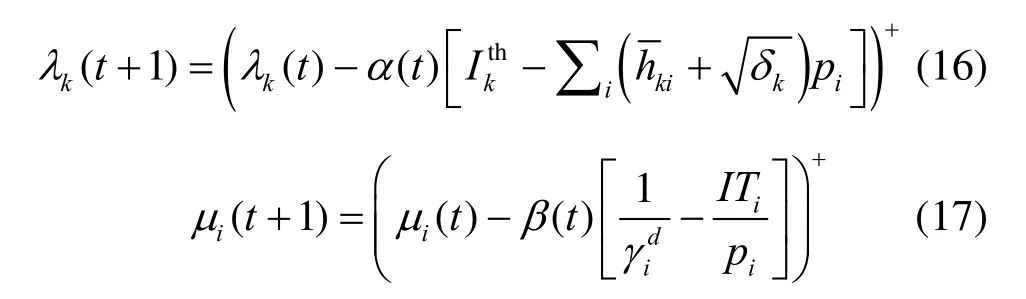
其中，（·）+=max（ 0,·），t为迭代次数，α(t)和β(t)为步长。只要步长选择足够小的正常数，便可保证次梯度更新算法收敛[14]。

顽健分布式功率控制算法流程如下所示。

1) 在t=0时，设置主变量和次变量的初始值以及系统环境参数，满足实际物理意义和解的存在性。即

2) 在次用户接收机端，通过最小二乘法或者参数估计理论获得信道，测量接收机处的干扰和噪声，并计算干扰与噪声和，考虑估计误差iε，计算ITi值；通过式(17)更新对偶变量通过反馈信道返回ITi和μi(t +1)的值。

3) 在同一信道上的发射机端，接收ITi和μi(t +1)的值；估计信道增益hki，接收来自其他用户的干扰功率和信道链路信息；考虑信道估计误差δk，计算总的干扰功率。通过式(16)更新对偶变量λk(t +1)，更新功率变量其中，popt(t+1)通过式(15)更新。

4) 如果功率和对偶变量都收敛则算法停止，否则返回2)。

由对偶变量更新式(16)可以发现，每个次用户之间需要进行干扰信道信息交换，这种方式仅适用于网络中用户数量少的情况。然而，当用户数量多时，次用户间大量的信息交换会影响算法的实时性和复杂度。为此，下面考虑另一种保守的功率分配算法。将约束式(1)可以考虑为对每个用户的干扰温度线，从而有如下形式

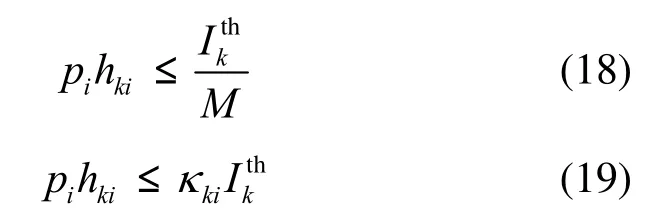
其中，式(18)为平均干扰约束，没有考虑次用户的远近效应，M为接入网络中的次用户个数，该约束可等价为式(19)表示考虑次用户公平性的干扰约束，kiκ为加权因子，且满足当次用户离主用户近时，次用户应该减小发射功率以免对主用户产生大的干扰，该次用户功率范围应该紧缩；如果次用户离主用户远，需要提高用户的发射功率以满足用户的QoS需求。假设信道衰减模型为代表路径衰减指数。因此，对于相同通信环境下（即路径衰减指数相同），可以简单设计；对于不同环境下，；如果某个信道条件很差的次用户发射最大功率仍然无法满足自身的QoS需求，将该信道上的用户发射功率分配为0，防止对其他次用户和网络中的主用户造成不必要的干扰，该问题需要通过接纳控制算法(admission control algorithm)来改变当前活动次用户的数量。

根据以上约束条件可得到如下改进顽健功率控制算法为

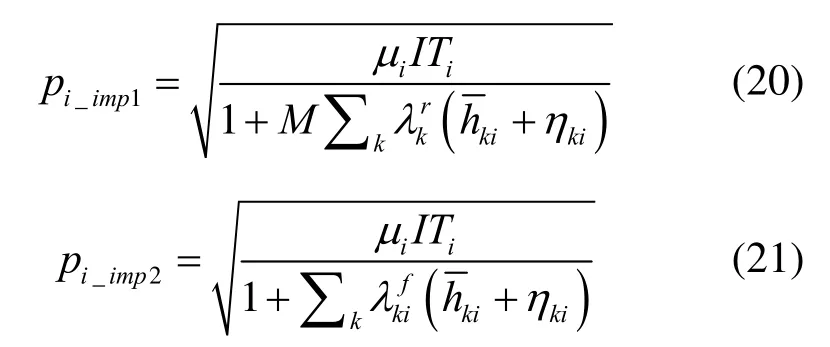
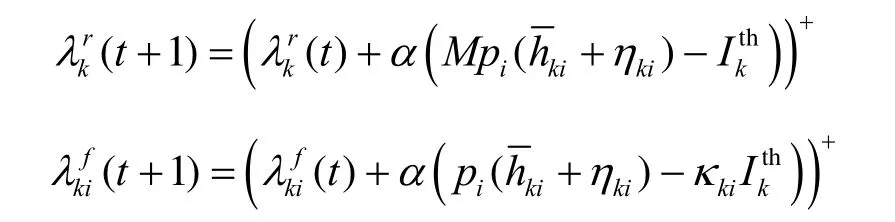
并且用户数量M和离主用户的距离kid可以分别用文献[15]和文献[16]中的方法得到。

4 仿真结果与性能分析

为了验证所提算法的有效性，从系统性能和用户QoS需求两方面比较了顽健功率分配算法和非顽健功率算法、SOCP算法的性能。为了便于分析，本文省略对改进算法的仿真结果。假设网络中有2对次用户和1对主用户，即M=2,N=1，系统中每个用户存在相同程度的不确定性。假设次用户发射机最大发射功率为，信道增益和噪声满足最小期望的SINR为

图1显示出估计误差bi在名义值附近随机变化，变化范围假设满足区间[-0.05,0.05]，信道gi不确定性对次用户接收信干噪比的影响。从图2中可以看出，本文提出的顽健算法能够保证实际SINR在参数摄动下不低于最小信干噪比γid，由于提前考虑了参数不确定性影响，能够保证每个次用户的服务质量，减小了用户的中断概率；然而，在不确定性情况下，非顽健算法不能保证在所有时刻都满足最小信干噪比约束式(3)，当实际接收到的信干噪比小于目标值γid时，将会发生通信中断。所以非顽健设计方法对信道变化不具有顽健性。

图1 信道不确定性iε对接收到SINR的影响

图2给出了在不同信道不确定性和最小SINR情况下，对系统性能（总功率消耗）的影响。假设每个信道的摄动程度相同，并定义摄动参数为从图2中可以看出，随着目标信干噪比γid的增加，所需要的发射功率也随之增大，从而使总的功率消耗增加。因为需要更多的发射功率来提高所需要的SINR性能。另一方面，随着不确定性增大，总的功率消耗随之增加。从式(9)可以发现，当估计误差越大，顽健算法需要更多的发射功率来抑制参数不确定性对系统性能的影响，防止接收机端实际的SINR小于最小SINR需求。从整个系统性能的角度来说，顽健算法通过牺牲系统最优性（总功率消耗最小）来保证每个用户的通信质量。而非顽健算法（ξ=0）由于没有考虑不确定性影响，总的功率消耗最少。

图2 信道不确定性对总功率消耗的影响

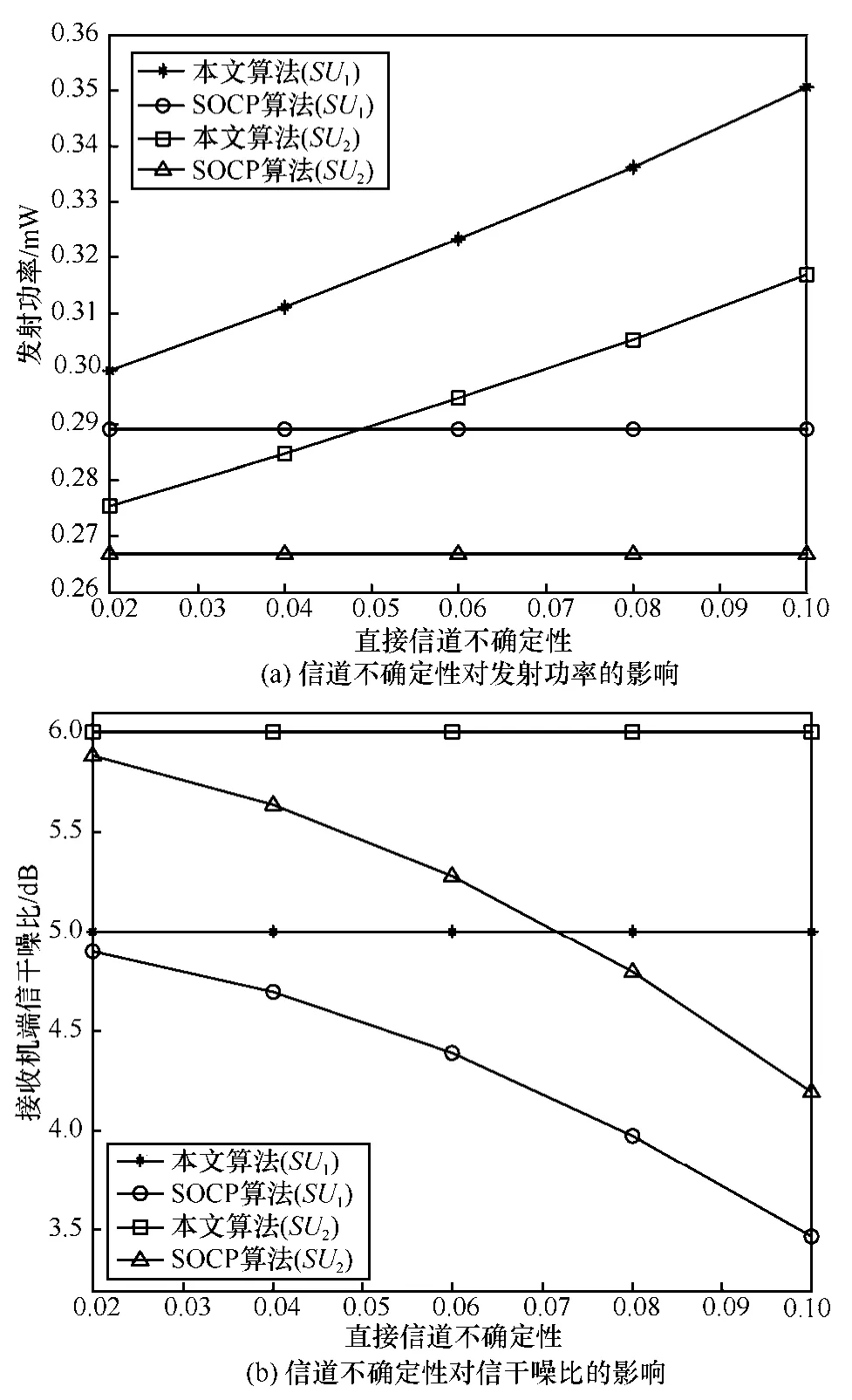
图3 本文算法与SOCP算法对比

图3是文献[13]中SOCP算法与本文算法信干噪比的对比。只考虑了直接信道参数不确定性的影响，并假设存在2个次用户和1个主用户存在的情况。最小信干噪比为15dγ=dB和26d γ=dB，背景噪声为0.03 mW。从图3(a)中可知，由于SOCP算法忽略了直接信道增益不确定性的影响，所以发射功率不变。然而，本文算法通过提高发射功率来克服该信道不确定性的影响。另外，从图3(b)中还可以看出，本文算法能够保证每个用户的服务质量，而SOCP算法无法满足该要求。所以，本文算法通过提高发射功率作为代价来满足不同用户的QoS需求。

图4给出了在参数不确定的情况下，用户数量对系统性能的影响。假设系统参数与图2中相同，参数摄动δk=εi=10-4。从图4中可以看出，随着网络中活动的次用户数量的增加，认知系统消耗的有效总功率增大。由于主用户数量的增加会对次用户带来更多的干扰，因此，当主用户数量增大会使得次用户发射机需要进一步提高发射功率来克服增加的干扰功率来维持次用户的信干噪比。同时，增加次用户数量，会使认知系统的总功率消耗增大。在同一通信环境下，当系统中成倍增加用户数量，系统能量总消耗会比对应比例多。例如用户数量(M=6,N=3)的功率消耗大于3倍的用户数量(M=2,N=1)的功率消耗。从次用户本身来讲，新接入的次用户不仅对系统的总能耗有贡献，并且对已存在的用户造成更多干扰，因此当前用户需要提高自己的发射功率来满足各自的QoS需求，以达到新的网络平衡。另一方面，从主用户方面来看，新增加的主用户收发机会对次用户接收机造成更多的干扰。

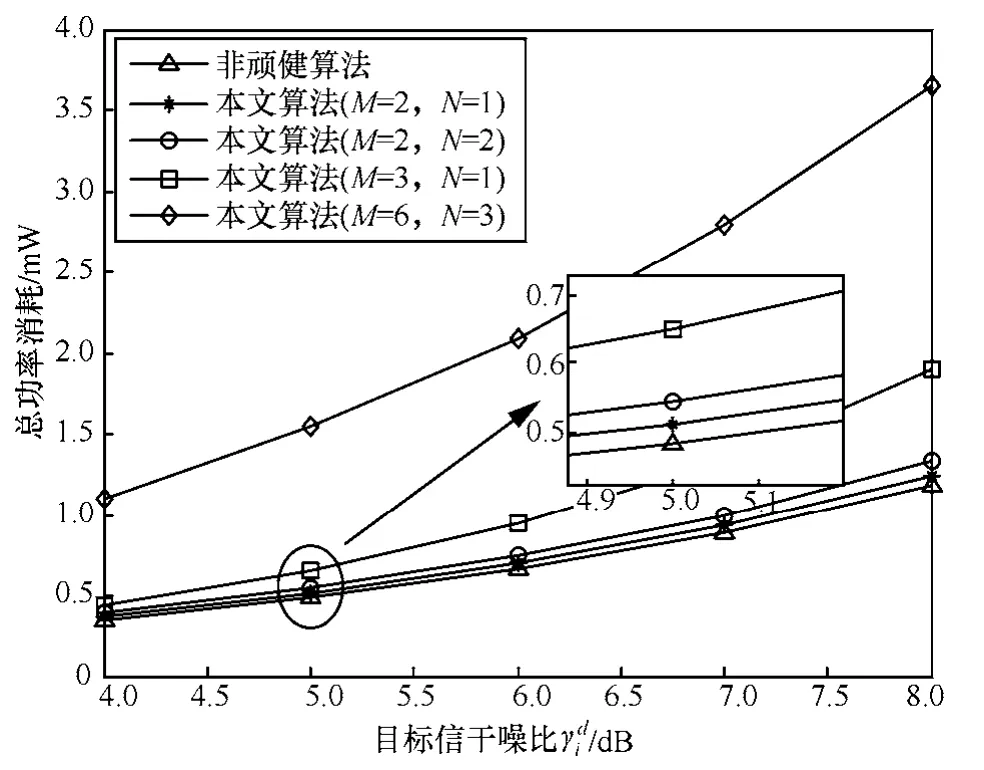
图4 不同用户数量对功率消耗的影响

5 结束语

考虑了干扰温度和信干噪比中参数不确定性的影响，讨论了认知无线电网络中以最小化发射功率为目标的顽健资源分配问题。基于欧几里得球形不确定性描述方法，在最坏约束条件下，将无穷维不确定性线性约束转换为有限维约束，从而将原优化问题转换为一个确定性凸优化问题。通过拉格朗日对偶原理和次梯度更新方法，得到顽健分布式最优解。仿真结果表明，所提出的算法可以保证在所有给出的可能估计误差条件下，仍然能够保证系统的通信质量，算法性能优于非顽健功率分配方法。

[1] HAYKIN S. Cognitive radio: brain-empowered wireless communication[J]. IEEE Journal on Selected Areas in Communications, 2005,23(2):201-220.

[2] GATSIS N, MARQUES A G, GIANNAKIS G B. Power control for cooperative dynamic spectrum access networks with diverse QoS constraints[J]. IEEE Transactions on Communications, 2010, 58(3): 933-944.

[3] NGO D T, NGOC T L. Distributed resource allocation for cognitive radio networks with spectrum-sharing constraints[J]. IEEE Transactions on Vehicular Technology, 2011, 60(7):3436-3449.

[4] ZHANG L, LIANG Y C, XIN Y, etal. Robust cognitive beamforming with partial channel state information[J]. IEEE Transactions on Wireless Communications, 2009, 8(8):4143-4153.

[5] ZHANG G , WONG K K, OTTERSTEN B. Robust cognitive beamforming with bounded channel uncertainties[J]. IEEE Transactions on Signal Processing, 2009, 57(12):4871-4881.

[6] JULIAN D, CHIANG M, NELL D O. Robust and QoS constrained optimization of power control in wireless cellular networks[A]. VTC 2001[C]. Altantic, NJ, 2001.1932-1936.

[7] ANANDKUMAR A J G, ANANDKUMAR A, LAMBOTHARAN S,etal. Robust rate maximization game under bounded channel uncertainty[J]. IEEE Transactions on Vehicular Technology, 2011, 60(9): 4471-4486.

[8] SUN S Q, NI W M, ZHU Y. Robust power control in cognitive radio networks: a distributed way[A]. ICC 2011[C]. Kyoto, Japan, 2011.1-6.

[9] SETOODEH P, HAYKIN S. Robust transmit power control for cognitive radio[J]. Proceeding of IEEE, 2009, 97(5):915-939.

[10] ANESE E D, KIM S J, GIANNAKIS G B, etal. Power control for cognitive radio networks under channel uncertainty[J]. IEEE Transactions on Wireless Communications, 2011, 10(10):3541-3551.

[11] PHUNCHONGHARN P, HOSSAIN E. Distributed robust scheduling and power control for cognitive spatial reuse TDMA networks[J].IEEE Journal on Selected in Communications, 2012, 30(10): 1934-1946.

[12] PARSAEEFARD S, SHARAFAT A R. Robust worst-case interference control in underlay cognitive radio networks[J]. IEEE Transactions on Vehicular Technology, 2012, 61(8):3731-3745.

[13] PARSAEEFARD S, SHARAFAT A R. Robust distributed power control in cognitive radio networks[J]. IEEE Transactions on Mobile Computing, 2013, 12(4): 609-620.

[14] BERTSEKAS D P. Nonlinear Programming 2nd ed[M]. Boston, MA:Athena Scientific, 1999.

[15] PERKINS C E, ROYER E M. Ad-hoc on demand distance vector routing[A]. IEEE WMCSA 1999[C]. New Orleans, 1999. 90-100.

[16] SAVIC V, ZAZO S. Reducing communication overhead for cooperative location using nonparametric belief propagation[J]. IEEE Wireless Communications Letter, 2012, 1(4):308-311.