认知无线电网络中基于主系统有限反馈的频谱共享方案

高欢芹，宋荣方,2

(1. 南京邮电大学 宽带无线通信与传感网技术教育部重点实验室，江苏 南京210003；2. 东南大学 移动通信国家重点实验室，江苏 南京210096)

1 引言

随着无线应用需求大量增长，无线频谱显得日益短缺。近年来，由Mitola J提出的认知无线电技术[1]被美国联邦通信委员会（FCC, federal communications commission）认为可以解决无线频谱短缺问题。认知无线电技术允许次用户（非授权用户）接入原先已经分配给主用户（授权用户）的频带，实现次用户和主用户频谱共享。在频谱共享过程中，一个突出问题就是管理和控制次用户机会接入对主系统引起的干扰。文献[2,3]在干扰温度约束下分别讨论了加性高斯白噪声（AWGN, additive white Gaussion noise）信道和瑞利衰落信道下主接收机的容量问题。文献[4]提出了一种称为速率损失约束（RLC, rate loss constraint）的干扰管理策略，同时文献[4]还表明在RLC约束下，认知系统能够获得比传统的干扰温度约束条件下更高的吞吐量。

为了对干扰进行管理并将干扰控制在主系统所能忍受的门限以下，认知无线电系统的发射端需要知晓主系统链路完整的信道状态信息。然而，得知完整的信道状态信息在实际情况下难以做到，几乎不可能实现。因此，基于信道信息有限反馈的认知无线电系统的设计被广泛研究。文献[5]研究了单小区认知无线电系统，基于小区中每个认知用户向基站反馈的量化信道信息实现动态资源分配。文献[6]提出了一种主用户采用自适应调制编码方案，但发送功率恒定的频谱共享方法。文献[7]对次信道及干扰信道采用广义劳埃德类型算法（generalized lloyd algorithm）进行联合量化，提出一种渐进量化功率分配算法。文献[8,9]研究了利用主网控制信道有限反馈使得次用户吞吐量最大化方案。值得注意的是，以上现有的研究均假定存在一个中心基站对主次用户之间的相互影响进行协调，而在实际的部署中这种情况很可能遭受局限，无法实现。文献[10]研究了一对主用户和一对次用户共存情况下基于主信道量化反馈的频谱共享方案。

本文的研究目标是在次用户发送端可获得主系统链路量化CQI条件下使次系统吞吐量最大化，同时满足主系统速率损失约束。本文中假定各主用户对次用户的存在毫无察觉，次用户作为一个被动的聆听者。各主用户信道质量信息（CQI, channel quality information）由主接收端进行估计、量化并反馈给主发射端。次用户发射机依据偷听到的主系统量化CQI适时地接入对应主信道。次用户的机会接入对各主用户造成一定干扰，以致主系统的传输速率遭受一定损失。本文提出了一种基于多个主用户CQI有限反馈的次用户频谱共享方案。研究得出了使次系统吞吐量最大化的发送功率与传输速率最佳分配方案，该方案同时能够满足主用户RLC约束。详细分析了发送端完全未知/已知主系统CQI时的最佳频谱共享方案，这2种情况可分别作为基于主系统CQI有限反馈的频谱共享方案的理论下限和上限。

2 系统模型

本文所研究的系统模型如图1所示，假设存在包含M个发射机和一个接收机的主系统，同时存在一对次用户收发信机。主用户发射机一直占用信道，次用户通过频谱共享的方式占用相同的信道。从发射机i（i∈{1,2,…,M,s}，1,2,…,M代表各主用户，s代表次用户）到接收机j（j∈{p,s}，p代表主接收机，s代表次接收机）之间的信道功率增益用gij表示。假定信道功率增益服从均值为的指数分布。

多个主用户以某种正交的方式同时与接收机之间进行数据传输。假定各主用户信道为块衰落信道，信道增益在一个块内保持不变，不同块之间发生变化并且相互独立。假定主接收机通过导频序列可完全获知主系统链路信道功率增益gip,(i={1,2,…,M})，通过有限反馈主发射机可得知信道功率增益的部分信息。依据信道功率增益的部分信息，主发射机从预先设计好的码本中选取某一发送功率及传输速率对，以突发方式进行数据传输。在一个块内的数据传输保持相同的发送功率及传输速率。在各主用户发送数据的同时，次用户根据偷听到的反馈信息尝试接入信道。假定次发射机已知主用户中预先设计好的量化码本，并假定发送端已知信道功率增益的均值。

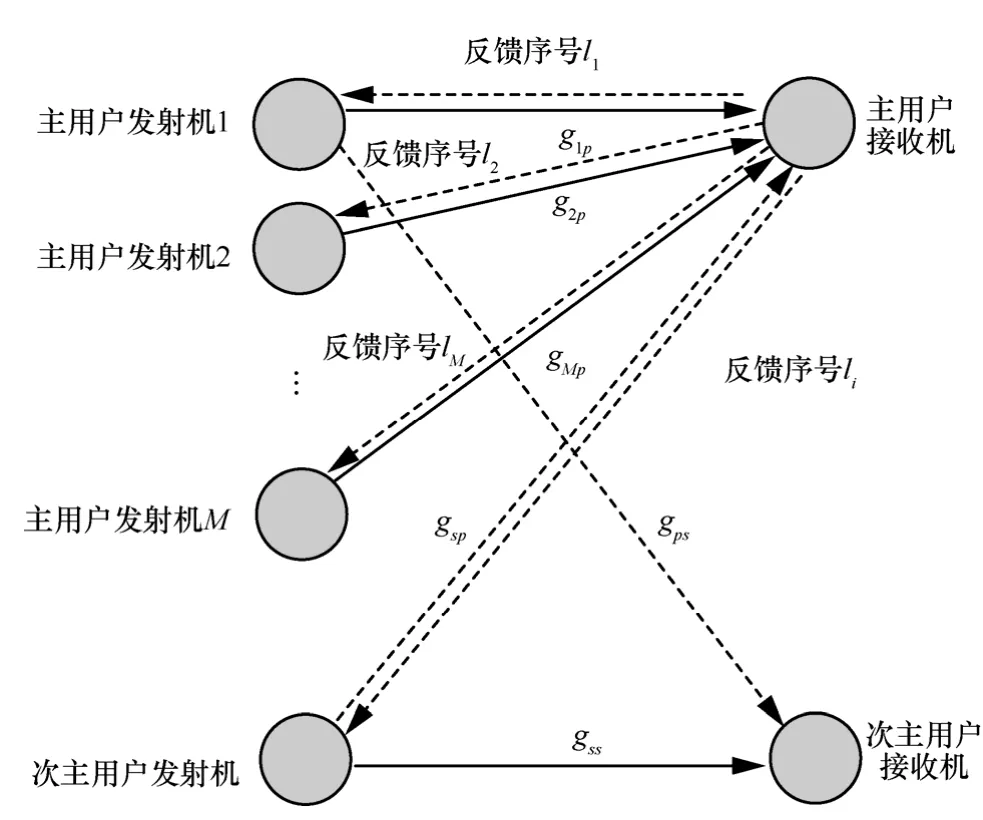
图1 基于主信道量化反馈的频谱共享系统模型

3 主用户量化码本设计

文献[11]提出了一种用于点对点通信系统的量化码本设计方法。本文采用与文献[11]中相同的码本设计方法。假定将代表各主用户信道质量的信道功率增益gip(i∈{1,2,…,M})量化成L个区间，即[0,γ1), [γ1, γ2),…,[γL-1,+∞)。用li(0≤li≤L-1,i={1,2,…, M})表示信道功率增益gip所在的量化区间对应的序号，序号越小表明信道质量越差。主接收机将序号li反馈给对应的主发射机i，所需要的反馈比特数为表示不小于x的最小整数。

各主发射机根据接收到的序号li从预设的码本中选取对应的发送功率与传输速率注1注1：本文中所有传输速率均是以自然对数为底，相应的速率单位为nats per second。进行数据传输，直到接收到下一个反馈序号重新选择对应的发送功率与传输速率。传输速率取决于量化门限及发送功率对于第i个主用户而言，传输速率、量化门限及发送功率三者之间关系式如下

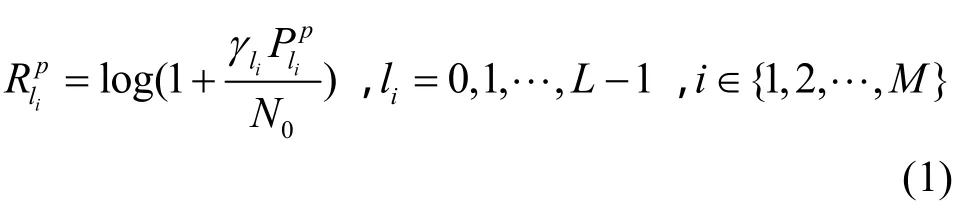
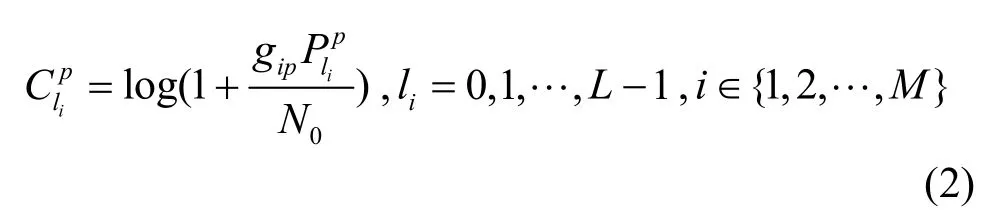
由于以下的分析对于各用户均成立，所以省去下标i。可以看出，当l≥1时，总是成立。但是，当l=0时，根据量化码本0≤gip＜γ1，而只有当时，才有成立。

用Fi(·)表示第i个主用户信道质量累积分布函数（CDF, cumulative distribution function），假设其信道功率增益服从均值为（i∈{1,2,…,M}）的指数分布，则定义第i个主用户的平均传输速率为

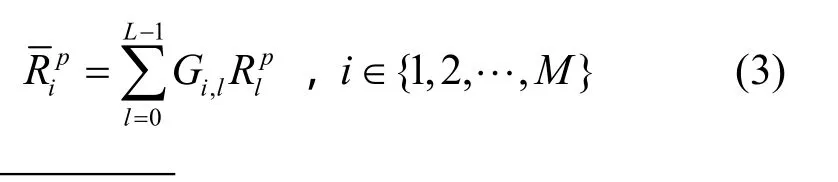
整个主系统的平均传输速率为

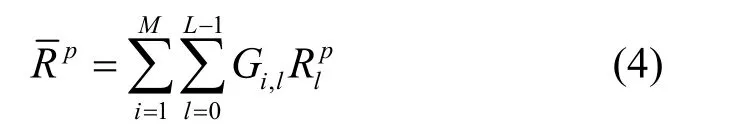
量化门限γl与发送功率Plp(l=0,1,…,L -1)可以通过使系统平均速传输率最大化来求得

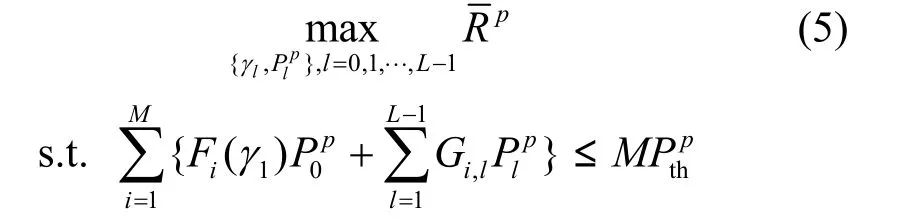
4 基于主用户有限反馈的频谱共享方案

假定次用户发射机可获知主系统的量化码本。在每个信道衰落块内，次用户根据偷听到来自于主接收机的反馈信息，即各主用户信道功率增益所在的量化区间序号，次发射机选择一对恰当的发射功率Ps及传输速率Rs进行数据传输。在每个块内，次用户均根据最小的量化区间序号，即来选择发射功率及传输速率。序号越小表明该主用户的信道质量越差，在利用多用户分集增益的系统中该用户所能带来的分集增益是最小的，那么次用户传输则占用该用户的信道进行传输。次用户传输对主系统速率所造成的影响要小于规定的速率损失约束。假设与最小序号ml对应的主用户为m。

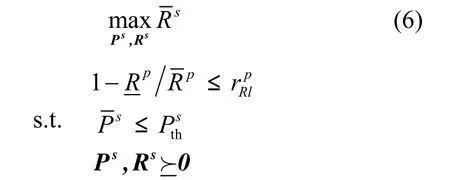
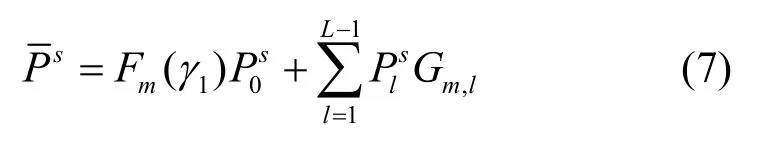
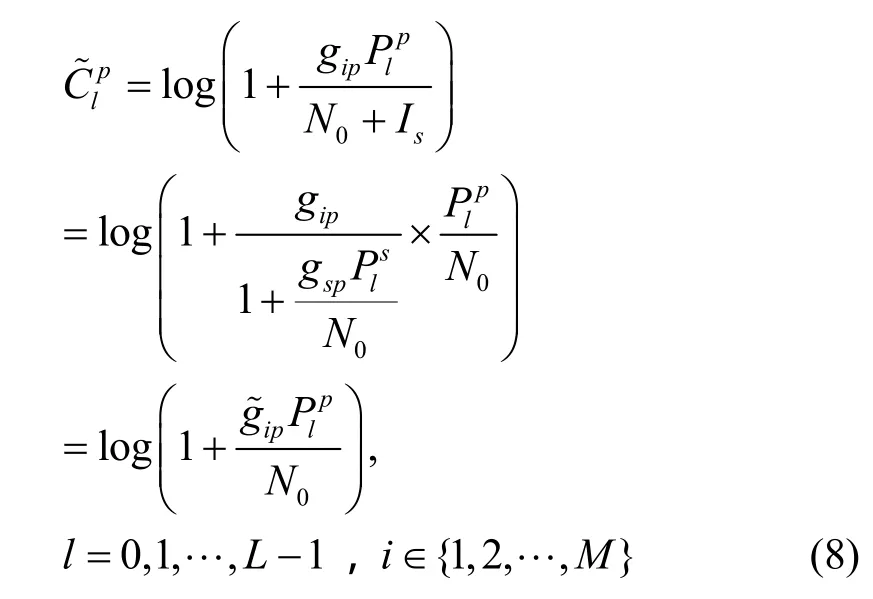
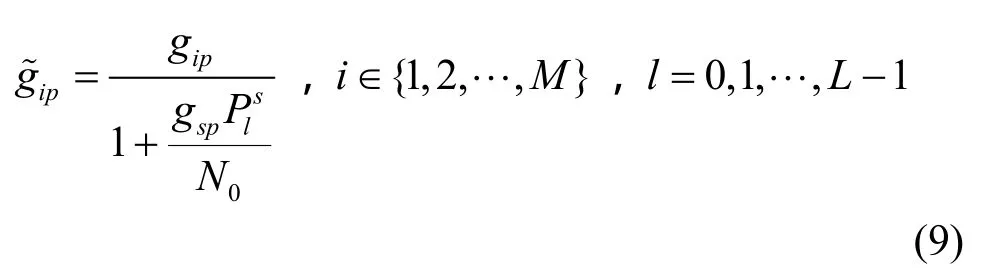
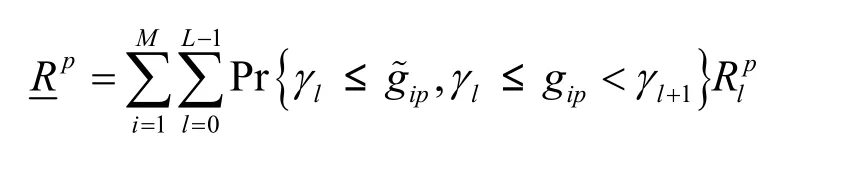
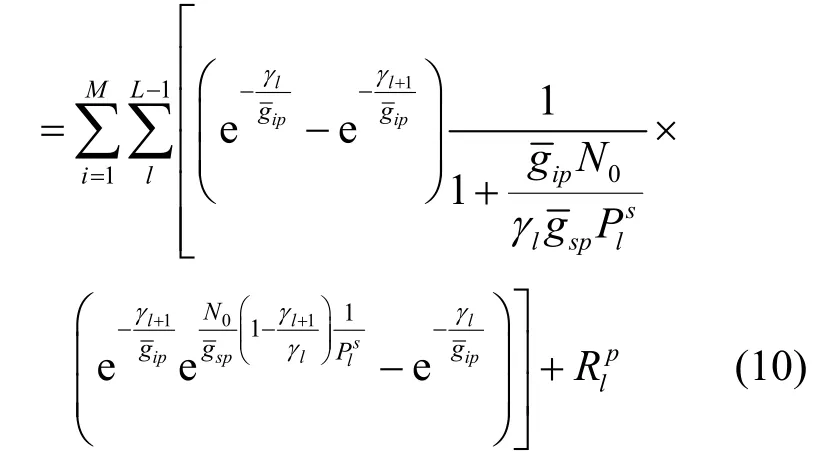
下面着手解决式(6)的最优化问题。不难发现式(6)所描述的频谱共享问题是个非线性、非凸优化问题，通常对于这类问题很难以多项式时间得以解决。然而，根据辅助定理1[10]，如果将次用户的传输速率Rs用次用户的发射功率Ps来表示，可以证明式(6)所描述的目标函数是下凹的。

式(6)中主系统速率损失约束也是个凹函数，因此式(6)所描述的速率最大化问题是个典型的微分凸问题，可以通过序列凸规划(SCP, sequential convex programming)方法有效地得以解决[12]。SCP的思想是将优化问题的下凹部分线性化，以致优化变量的可行域收缩到一个凸集，从而将问题转化为凸问题；然后，利用最后一轮解持续对近似值进行修正直到目标函数收敛至最优点。值得注意的是，在SCP规划中有两点很重要[12]：1)最后的解可能是局部的而非全局最优的；2)有时可能会很难找到一个初始可行点。

在本文所研究的问题中不存在以上2个问题。首先，由于信道衰落分布的连续性，式(6)满足文献[13]中所描述的“时间共享”条件。主次系统的功率分配方案共享相同的信道增益瞬时，从而信道衰落的瞬时共享替代了时间共享。因此，只要满足卡罗需－库恩－塔克(KKT, Karush-Kuhn-Tucker)条件的任一局部最优解均为全局最优解。其次，可以将次用户最初的发射功率设置成一个非常小的值来保证找到一个初始可行点，同时能够满足RLC约束与平均发射功率约束。

5 主发射机完全不知/已知CQI时次系统吞吐量分析

本节分别研究主系统发射机完全不知和已知主系统CQI时次系统吞吐量性能。2种情况可以分别作为基于主系统CQI有限反馈的次系统平均吞吐量性能理论下限与上限。

5.1 完全不知CQI

主发射机完全不知CQI相当于主接收机根本不反馈CQI。可将主系统的量化区间视为只包含[0,γ1)，并且γ1=+∞，各主发射机不管信道衰落如何变化，均保持恒定的传输速率及固定的发射功率P0p进行数据传输。这种情况下主系统根本无法获得多用户分集增益。根据式(4)可以得到该情况下主系统平均传输速率

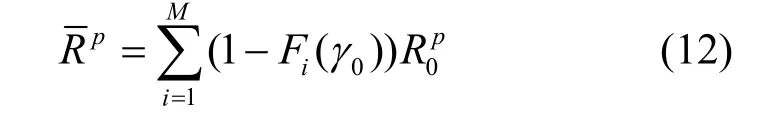
通过寻找最优的0γ可使主系统平均吞吐量最大化

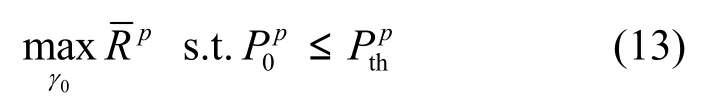
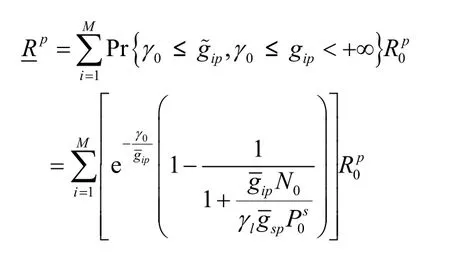
出现次用户传输时，根据式(10)可得到主系统平均传输速率为

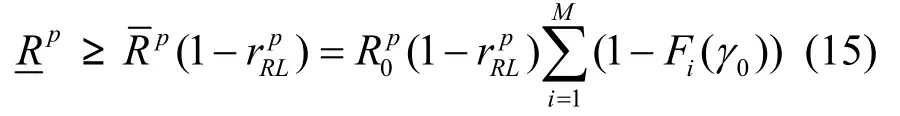
由式(14)和式(15)，可以得到次系统发射功率

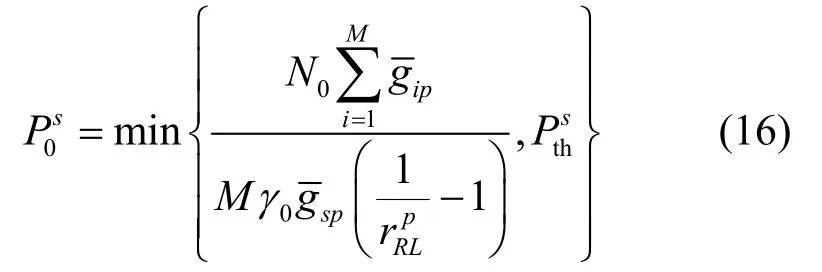
根据式(11)将次用户平均传输速率最大化即得到次用户发射机完全不知主系统CQI时次系统吞吐量

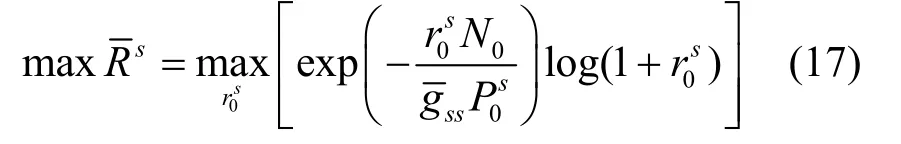
5.2 完全已知CQI

下面详细分析主次发射端均准确知晓各主用户信道增益gip(i∈{1,2,…,M})时次系统吞吐量性能。本文的分析与文献[4]的区别在于，本文中假设次用户发射端仅知晓次用户链路的部分信道信息，即信道指数衰落分布的均值。因此，对于本文中次用户发射功率分配不能直接采用文献[4]中所提出的改进注水方法。假定主系统接收机反馈的最小量化区间序号所对应的主用户为m，用户m所对应的信道增益为gmp。本文试图得到使次系统吞吐量最大化的次用户功率分配方案，同时能够满足与主接收机有限反馈时相同的主系统RLC约束。对于主发射机而言，由于完全知晓信道增益的准确信息，可以直接采用最佳注水功率分配方案。在此情况下，可以得到类似于式(6)的最优化问题

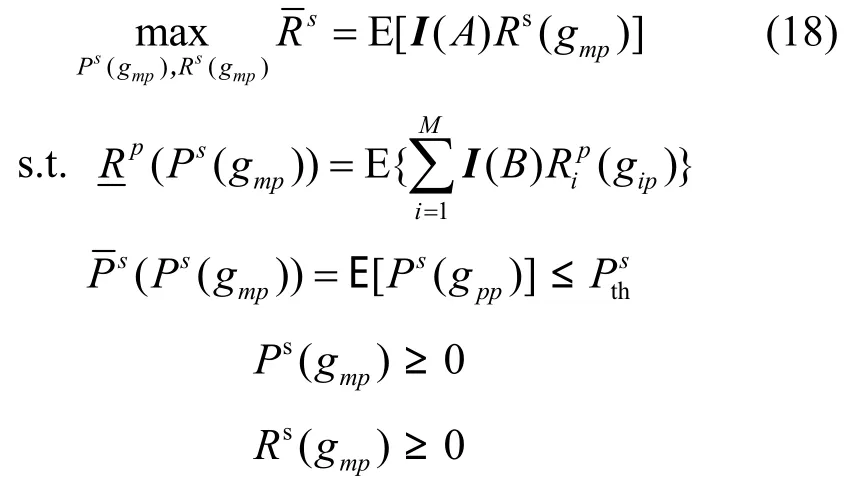
其中，()ΛI为指示函数(如果Λ为真，函数值为1，否则为0)，A、B分别表示以下2个事件

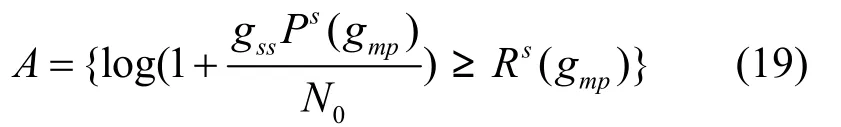
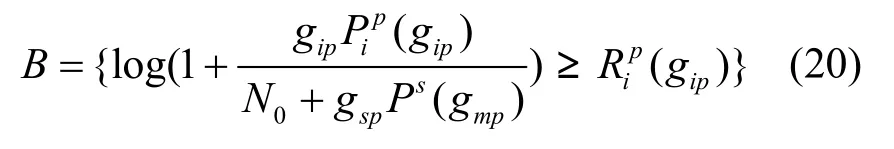
假设主系统采用精确的功率控制，来自于次系统任意小的干扰功率均会使得主系统的传输中断。次用户只能当mpg在区间[0,)pRLγ时进行传输，主用户在该区间内所能获得的吞吐量极为有限甚至为0，如图2所示。

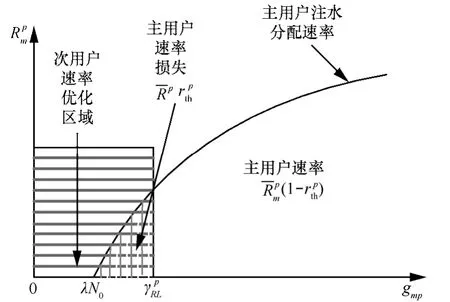
图2 完全已知主系统CQI时次用户功率分配

进一步分析之后，得到相应的次用户平均传输速率为

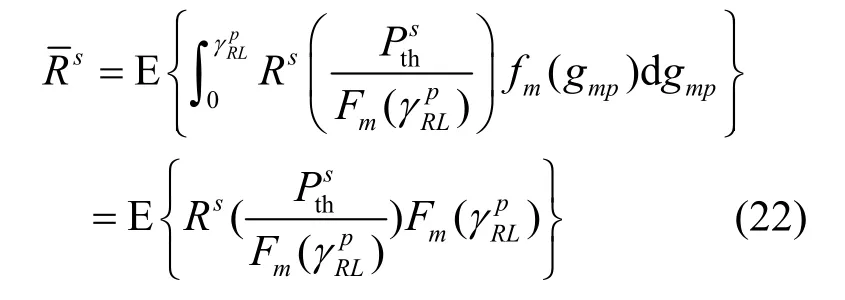
6 数值分析与仿真结果

本节通过数值分析与仿真验证本文所提出的频谱共享方案，并给出数值分析与仿真结果。图3给出了主系统包含2个主用户情况下，主系统平均传输速率随着主系统平均功率约束变化而变化的情况。2个主用户信道功率增益均值分别为：次用户信道功率增益均值为：，次用户发射机到主系统接收机之间的信道功率增益为：，噪声功率N0=1W。从图3可以看出增加反馈比特数能够带来主系统平均传输速率的提高。

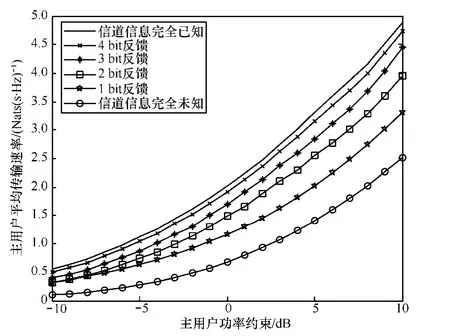
图3 主系统平均传输速率

表1给出了主系统包含2个主用户情况下，不同反馈比特数所对应的量化区间及各量化级门限值。

图4显示了次用户吞吐量随着其平均发射功率约束变化而变化的情况。图4中，主系统平均每用户发送功率约束与噪声功率N均为1 W，主系统0速率损失约束为10%。本文分别分析了主接收端对每个主用户CQI量化反馈的比特数为1，2，…，4的情况下次用户平均吞吐量。从图4可以看出只需要反馈3～4个量化比特，次用户平均吞吐量就很接近于主发射机均完全已知主系统信道增益时的情况；从曲线上还可看出当完全不反馈或只反馈1个比特时，随着功率约束持续增加次用户平均吞吐量增加到某个值之后就不再增加，而是趋于水平线，这是因为主系统的速率损失约束限制了次用户实际的发送功率增加。当反馈比特数超过2之后，主系统在第一个量化区域[0,γ1]中分配的功率通常为次用户能够将所有的功率注入到该区域中，从而使得次系统吞吐量性能得以提高。

表1 反馈不同比特个数所对应的量化区间及各量化级门限值(th5p P=dB，0=0NdB)

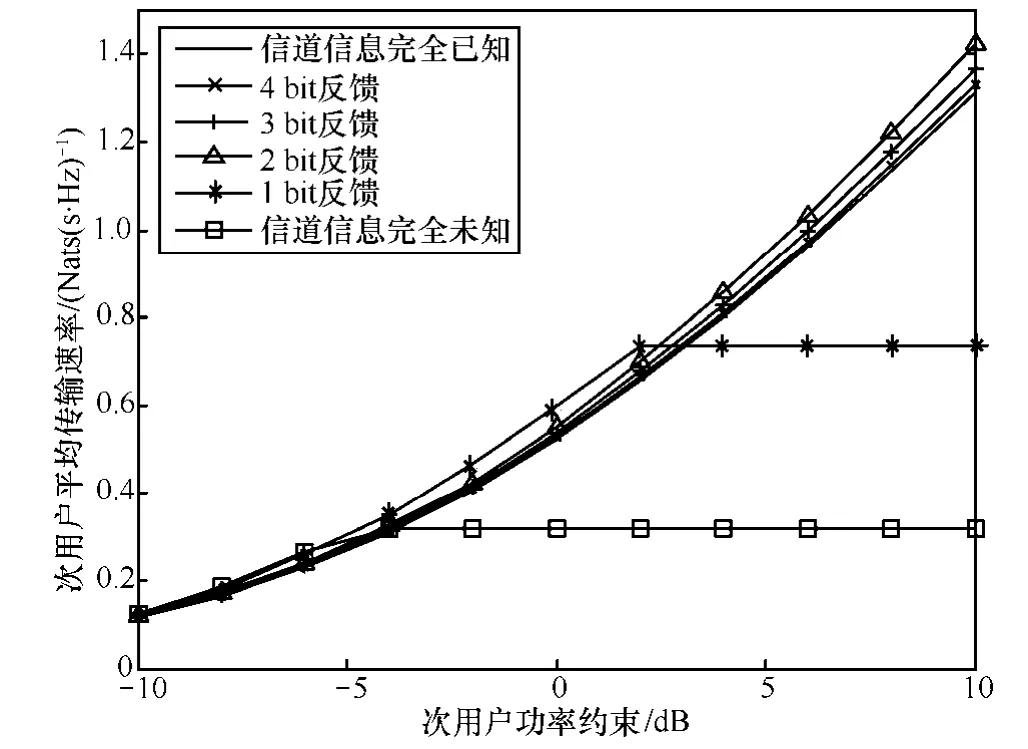
图4 CQI反馈比特数不同时次用户吞吐量

表2给出反馈不同比特数时，次系统对应于各量化区间发射功率与传输速率。

表2 次系统发射功率与传输速率(th5s P=dB,0=0NdB)

图5显示了当量化区域个数L=4(即反馈比特为2)，速率损失约束从10%增加到50%时，次用户发送功率在各量化区域的分布情况。由图5可以看出，次用户在各量化区间中所分配的发射功率随着速率损失约束的变化会发生很大变化。图5从左向右，通过图中带方块的曲线可以看出，随着增大(即速率损失约束放松要求)，次用户可获得的平均速率有所增加。从右向左，随着减小(即速率损失约束愈来愈苛刻)，可以看出次用户越来越倾向于将较多的功率分配给对应于主用户信道质量较差的那个区域。这么做的原因在于，在频谱共享的认知无线电网络中，如果主用户在某个量化区域中分配发射功率为0，那么主接收端就没有必要设置任何干扰温度门限，从而次用户在此区域中可以分配较大的发射功率。相反，当速率损失约束放松要求时，次用户发射机试图在各量化区域中进行等功率分配，以获得更高的吞吐量性能。

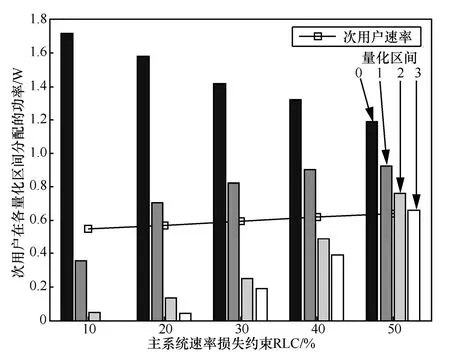
图5 不同速率损失约束下次用户发射功率分配及平均传输速率(th0s P=dB)

图6为主系统包含2个用户时，依据表1和表2所得出的量化门限值及次用户发射功率与传输速率对表，所得到的主、次系统传输速率仿真结果。仿真中，主次系统的信噪比均为5 dB，主次系统的信道功率增益均服从指数衰落分布，主系统中2个主用户信道功率增益的均值分别为：次用户信道功率增益的均值为：，次用户发射机到主系统接收机之间的信道功率增益为：由图6可以看出当主系统CQI量化反馈由0 bit增加到4 bit时，主系统的传输速率在出现次用户传输与不存在次用户传输相比均有所下降，但由于次用户传输所造成的传输速率的损失基本能够满足主系统的速率损失要求。从图中还可看出，牺牲了一小部分主系统传输速率能够换取次用户与主用户同时传输，实现主次用户频谱共享。

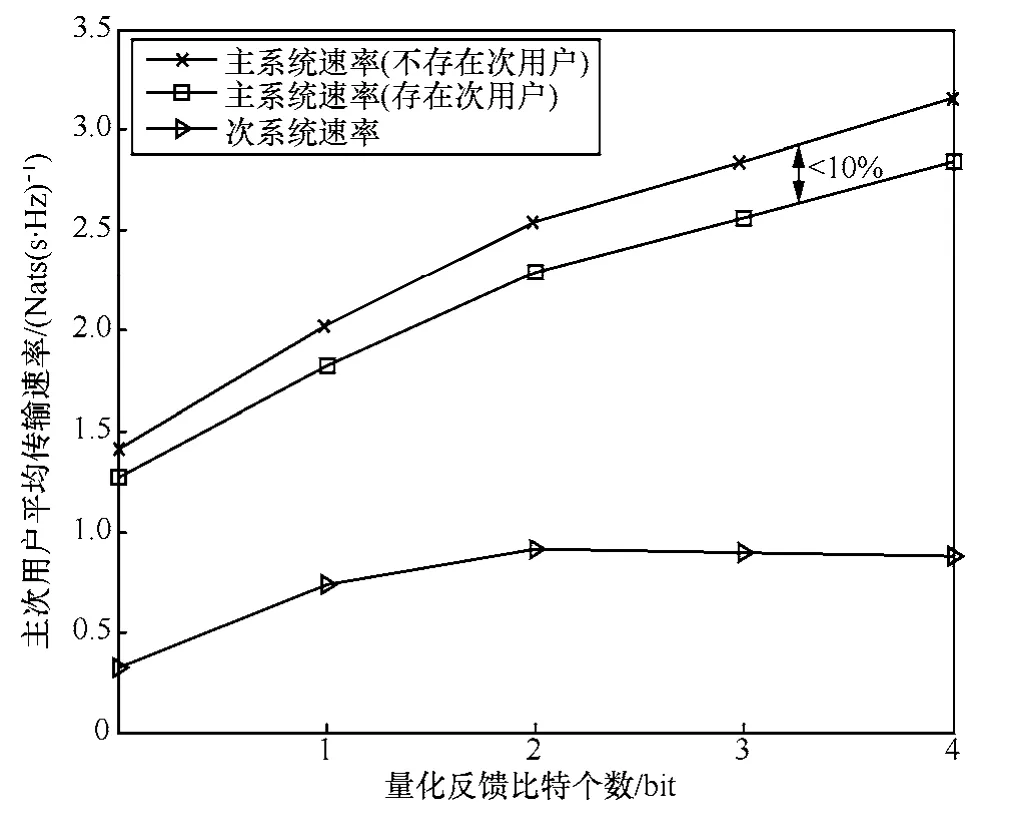
图6 存在和不存在次用户传输时主系统传输速率比较

7 结束语

本文提出了一种认知无线电网络中基于主系统有限反馈的频谱共享方案，适用于一对次用户收发信机与多个主用户共存的网络结构。次用户根据偷听到的主系统信道质量信息的量化反馈，可确定使得次系统吞吐量最大化的发射功率及传输速率最佳分配方案，同时能够满足次用户平均发射功率约束及主系统速率损失约束。数值分析结果表明，主接收端对于每个主用户信道质量信息只需要反馈3～4个量化比特，次系统的吞吐量就可堪比于主次发射端均完全已知主系统信道质量信息时的情况。仿真结果显示所提出的频谱共享方案能够满足主系统的速率损失约束。

附录 式(10)的推导过程

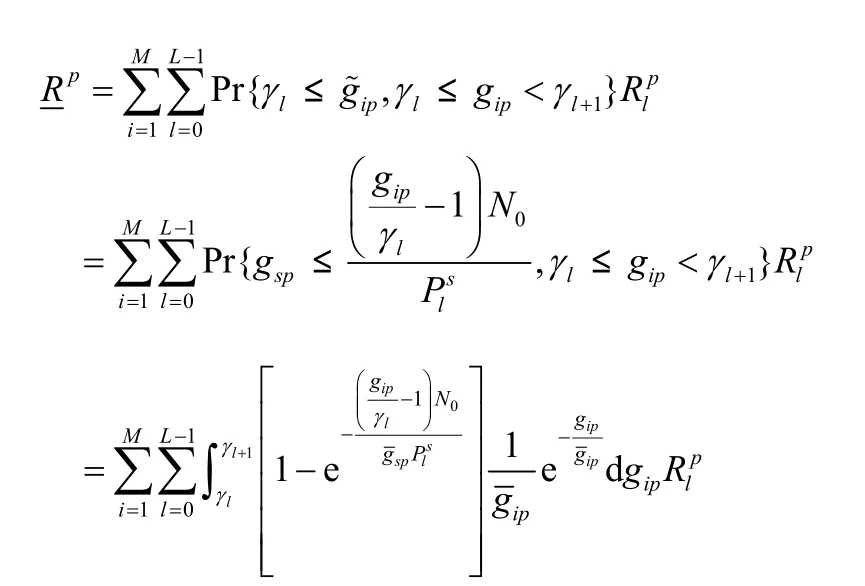
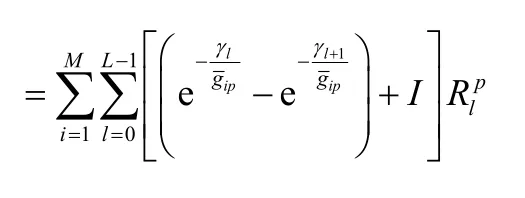
其中，

[1] MITOLA J, MAGUIRE G Q. Cognitive radios: making soft-ware radios more personal[J]. IEEE Personal Communications, 1999, 6(4):13-18.

[2] GASTPAR M. On capacity under receive and spatial spectrum-sharing constraints[J]. IEEE Transactions on Information Theory, 2007, 53(2):471-487.

[3] GHASEMI A, SOUSA E S. Fundamental limits of spectrum-sharing in fading environments[J]. IEEE Transactions on Wireless Communications, 2007, 6(2): 649-658.

[4] ZHANG R. Optimal power control over fading cognitive radio channel by exploiting primary user CSI[A] Proceedings of IEEE Global Communications Conference[C]. 2008.1-5.

[5] MARQUES A G, WANG X, GIANNAKIS G B. Dynamic resource management for cognitive radios using limited-rate feedback[J]. IEEE Transactions on Signal Processing, 2009,57(9):3651-3666.

[6] TAKI M, LAHOUTI F. Spectral efficiency optimized adaptive trans-mission for interfering cognitive radios[A] Proceedings of IEEE International Conference Communications[C]. 2009.1-6.

[7] HE Y, DEY S. Power allocation in spectrum sharing cognitive radio networks with quantized channel information[J]. IEEE Transactions on Communications, 2011, 59(6):1644-1656.

[8] HUANG S, LIU X, DING Z. Decentralized cognitive radio control based on inference from primary link control information[J]. IEEE Journal on Selected Areas in Communications, 2011, 29(2):394-406.

[9] ESWARAN K, GASTPAR M, RAMCHANDRAN K. Cognitive radio through primary control feedback[J]. IEEE Journal on Selected Areas in Communications, 2011, 29(2):384-393.

[10] JAMES C F, ZHANG W, YUAN J H. Opportunistic spectrum sharing in cognitive radio networks based on primary limited feedback[J].IEEE Transactions on Communications, 2011, 59(12):3272-3277.

[11] KIM T T, SKOGLUND M. On the expected rate of slowly fading channels with quantized side information[J]. IEEE Transactions on Communications, 2007, 55(4):820-829.

[12] BOYD S P. Sequential convex programming[EB/OL]. http://www.stanford.edu/class/ee364b/lectures/seq_slides.pdf.

[13] YU W, LUI R. Dual methods for nonconvex spectrum optimization of multicarrier systems[J]. IEEE Transactions on Communications, 2006,54(7):1310-1322.

[14] LUO J, YATES R, SPASOJEVIC P. Service outage based power and rate allocation for parallel fading channels[J]. IEEE Transactions on Information Theory, 2005, 51(7):2594-2611.