考虑不同桩土接触模型的深水钻井导管承载能力数值分析*

王宴滨 高德利 房 军

(中国石油大学(北京)石油工程教育部重点实验室)

考虑不同桩土接触模型的深水钻井导管承载能力数值分析*

王宴滨 高德利 房 军

(中国石油大学(北京)石油工程教育部重点实验室)

采用合理的桩土接触模型对正确计算深水表层导管的承载力具有重要意义。建立了深水导管横向位移和竖向承载力的计算模型,并用ABAQUS有限元软件,考虑初始地应力的影响,通过编写相应本构模型的有限元程序,用接触力学法和接触面单元法模拟了导管的横向位移,用库伦摩擦模型与Goodman接触单元模型模拟了导管的竖向承载力。结果表明:采用接触面单元法计算的导管横向位移大于接触力学法计算结果,采用Goodman模型计算得到的导管竖向承载力大于库伦摩擦模型计算结果。同时,分析了导管顶部竖向力及弯矩对导管横向位移,以及导管尺寸对导管竖向承载力的影响规律,对深水钻井导管工程设计与控制具有参考价值。

深水钻井;表层导管;桩土接触模型;横向位移;竖向承载力;数值分析

深水钻井导管是深水油气井建设过程中安装的第1层套管,后续的水下井口和防喷器组的重量及隔水管底部传递的外力全由此导管承受。由于浮式钻井平台(船)的漂移,将会使导管发生挠曲变形,如果深水钻井导管横向位移过大,会造成井口失稳[1-4]。深水海底泥线以下的浅部地层成岩性差、强度低,所以深水钻井导管采取喷射安装,一般不固井,如果此导管竖向承载能力不足,则有可能导致水下井口下沉甚至井眼报废等严重后果。因此,研究深水钻井导管承载能力,对于研究水下井口稳定性具有实际意义。苏堪华等[5]采用理论分析的方法得出了在顶部竖向力与弯矩作用下的导管挠曲微分方程,在求解方程中需要通过桩土接触理论计算导管外壁摩阻力,而且不同的接触模型计算所得的结果不同,准确计算导管外壁摩擦力依赖于海底土壤力学参数的准确获得;李基伟[6]采用ABAQUS有限元软件模拟了导管的横向承载力,所考虑的导管与海底土壤的接触模型为弹簧模型,没有考虑不同的桩土接触模型对导管横向位移的影响,在计算过程中也没有进行地应力平衡,所计算结果可能与实际情况偏差较大。目前也少有关于考虑导管与海底土壤不同接触面模型来计算导管的竖向承载力方面的文献报道,而合理的选择桩土接触面模型对正确计算导管的承载力非常重要。笔者根据土力学和桩基理论建立了适于深水钻井导管承载能力的理论模型及求解方法,并应用有限元软件ABAQUS考虑桩土接触面的不同模型,对喷射安装后的深水钻井导管承载能力进行了数值模拟,其结果对于深水钻井导管工程设计与控制具有参考价值。

1 导管承载力理论模型的建立及求解方法

1.1 横向承载力分析模型

为建立与海底土层相互作用下导管横向承载力分析模型,设作用于导管上的横向弯矩为Mt,竖向载荷为Nt,泥线以下支撑导管地基中产生的连续分布反力为,则深水钻井导管与海底土层相互作用的分析模型如图1所示。

通过力学平衡关系,可得到导管在横向弯矩和竖向力共同作用下的挠曲微分方程为[5]

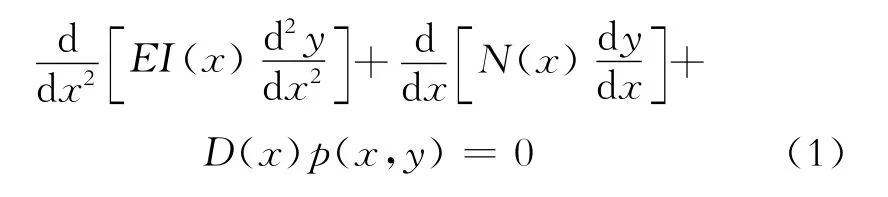
式(1)中:EI(x)为导管沿x方向的抗弯刚度,kN·m2; N(x)为导管沿x方向变化的轴向力,kN;D(x)为导管外径,m;p(x,y)为导管单位面积上的地基反力,kPa。

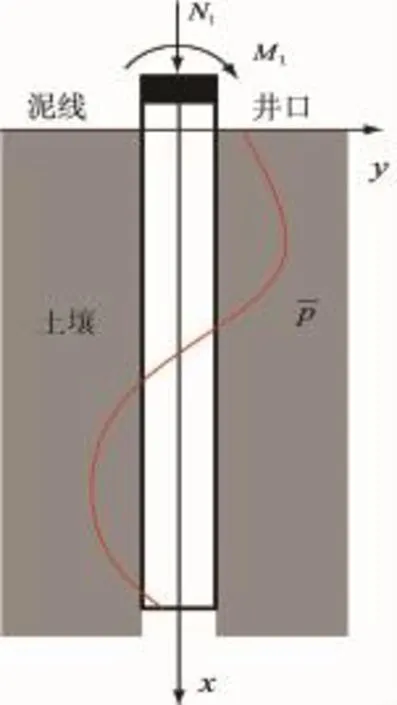
图1 深水钻井导管与海底土层相互作用的分析模型

1.2 竖向承载力分析模型

喷射下导管作业工序为:先喷射下入导管,不固井;继续钻入下表层套管的井眼,表层套管、水下井口与防喷器等都悬挂在导管上;然后注水泥固结导管与表层套管。其中,深水钻井导管竖向承载力分析模型如图2所示。

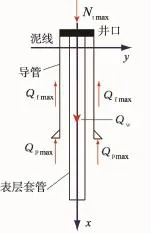
图2 深水钻井导管竖向承载力分析模型

要使导管保持稳定,其竖向受力关系须满足

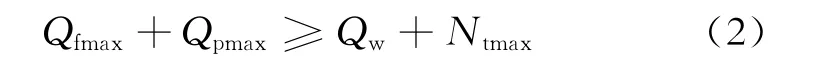
式(2)中:Qfmax为导管极限侧阻力,kN;Qpmax为导管极限端阻力,kN;Qw为导管自重,kN;Ntmax为导管能承受的最大竖向载荷,kN。

根据土力学原理及桩基理论可以计算出导管的极限侧阻力与极限端阻力,根据式(2)便可计算得到导管允许承受的最大竖向载荷。导管的竖向承载力主要由导管周围的海底浅部地层对其侧面产生的摩擦阻力和对其底端产生的支承阻力组成[7-8]。若忽略二者之间的相互影响,则导管的极限竖向承载力可表示为

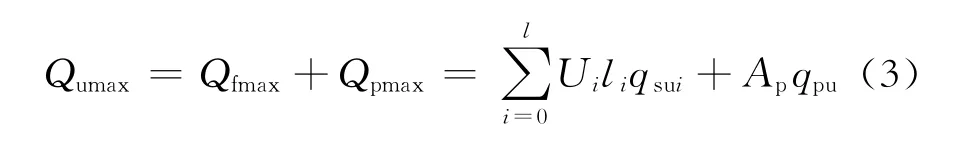
式(3)中:Qumax为导管的极限竖向承载力,kN;li为第i层土的厚度;Ui为第i层土处对应的管柱周长,m;l为管柱的入泥深度,m;qsui为管柱周围第i层土的单位面积极限管侧阻力,kPa;Ap为管端底面积,m2;qpu为单位面积极限管端阻力,kPa。

2 导管承载力有限元模拟方法

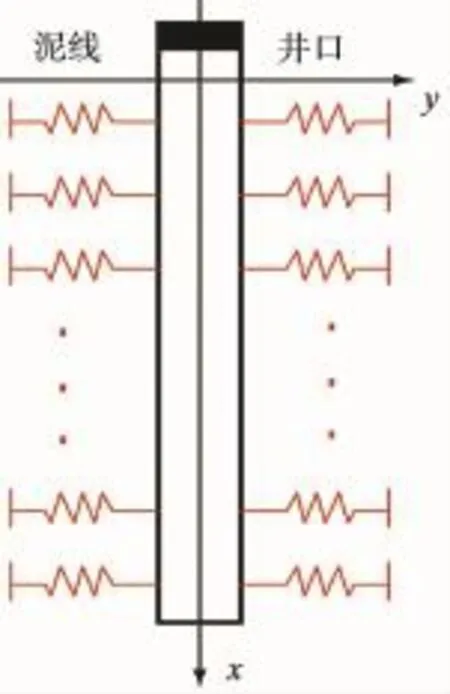
图3 接触力学法建立的深水钻井导管受力二维模型

2.1 横向承载力模拟方法

在进行桩土接触问题的有限元分析中,存在接触力学法和接触面单元法两大类。其中,接触力学法是用非线性弹簧来代替桩土之间的相互作用进行分析,而接触面单元法是通过添加接触面单元来模拟桩土之间的相互作用。

1)接触力学法分析。依据接触力学法[9]建立的深水钻井导管受力二维模型如图3所示,其中在泥线以下的导管被转换成插入土壤中的等强度的梁。在ABAQUS有限元分析软件中,用非线性弹簧来代替土壤对导管的非线性作用力,弹簧的性质是根据各层土壤的性质来确定。根据土力学原理确定的等价土弹簧刚度k为

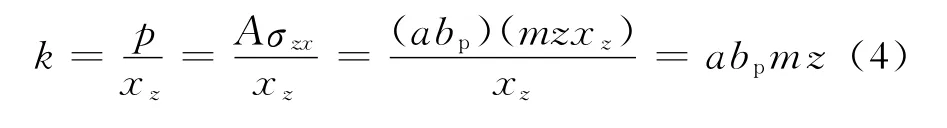
式(4)中:a为典型的计算单元厚度;bp为土层在垂直于计算模型所在平面上的宽度,对于圆柱形桩取bp=0.9(D+1),D为桩径。

2)接触面单元法分析。接触面单元法中最具代表性的是1968年古德曼[10-11](Goodman)提出的一种4结点无厚度单元模型,如图4所示。此模型假设在2种材料的接触面上存在无数正交的微小弹簧,接触面单元充分考虑了接触界面间位移的不连续性,应力应变关系属于非线性弹性,其本构关系如式(5)所示:

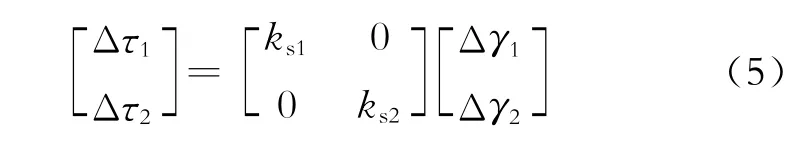
式(5)中:Δτ1和Δτ2分别为接触面上切向应力和法向应力;ks1和ks2分别为单元切向和法向弹性系数, Δγ1和Δγ2分别为单元切向和法向相对位移。式(5)所示的本构关系在ABAQUS软件中没有设置,需要自己定义。具体实现方法为通过Fortran语言编写代码,自定义接触面子程序FRIC,加载到ABAQUS中,在计算过程中调用。

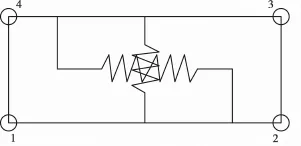
图4 Goodman提出的4结点无厚度单元模型[10-11]

2.2 竖向承载力模拟方法

在计算深水钻井导管的竖向承载力时,选择不同的桩土接触面模型,意味着采取不同的桩侧接触切向摩擦力算法[12-16],这对计算导管竖向承载力至关重要。

1)库伦摩擦模型。ABAQUS软件中默认的接触切向摩擦力算法为库伦摩擦模型,并且定义:当接触面上的剪应力小于临界摩擦剪应力时,接触面处于无相对运动的粘结状态,此时的摩擦剪应力属于静摩擦力;当接触面上的剪应力大于等于临界摩擦剪应力时,接触面开始发生相对滑移[17]。

2)Goodman单元模型。由于Goodman单元模型考虑了接触界面间的位移不连续性,应力应变关系属于非线性弹性,因此得到了广泛的应用。

2.3 初始应力场平衡

在深水钻井导管没有贯入海底土层之前,土体内部由于受到自重及上部海水压力的作用,存在着原始的应力场。是否有初始地应力场对桩土相互作用模拟结果有很重要的影响,因此必须加以考虑[18]。初始地应力平衡的目的在于保证在土体位移为零(一般在10-4m左右即可)时内部存在初始应力。对于表面不规则的土体,可以采用初始应力提取法。首先将已知边界条件和自重施加到模型上,得到此时的模型应力场;然后将每个单元的应力外插到形心点,导出所有应力分量,将这些应力分量再施加于原有模型重新计算,就可以得到地应力平衡后的应力场,基本能保证各点的初始位移为零。

3 算例分析

3.1 计算数据

合理的导管入泥深度是确保深水钻井导管竖向承载力的关键。导管入泥深度既不能过大也不能过小,如果深度不够,导管能提供的极限承载力不足,在后续的作业中可能出现井口下沉;如果深度过大,又会使喷射过程耗费时间增多,成本增加,并且如果出现喷射不到位,将导致井口头过高,坐上防喷器后可能出现井口失稳的风险[19-20]。目前我国南海常用的导管外径主要有914.4mm和762.0mm两种,导管入泥深度通常在72m左右(6根导管),井口出泥面在2～3m,最大不能超过5m。算例中,假设喷射下入的导管外径为914.4mm,壁厚为25.4mm;导管入泥深度为72m,井口出泥面高度为3m,顶部受到的弯矩为3×106N·m;导管钢材弹性模量为210 GPa,泊松比0.3,密度为7 800 kg/m3。为了降低边界效应的影响,分析过程中土体径向取20倍桩径。为使模拟结果更接近实际,根据相关钻孔资料,将南海某地区海床下80m以内的地层规划成6个工程地质层[5],土体的具体材料参数见表1。

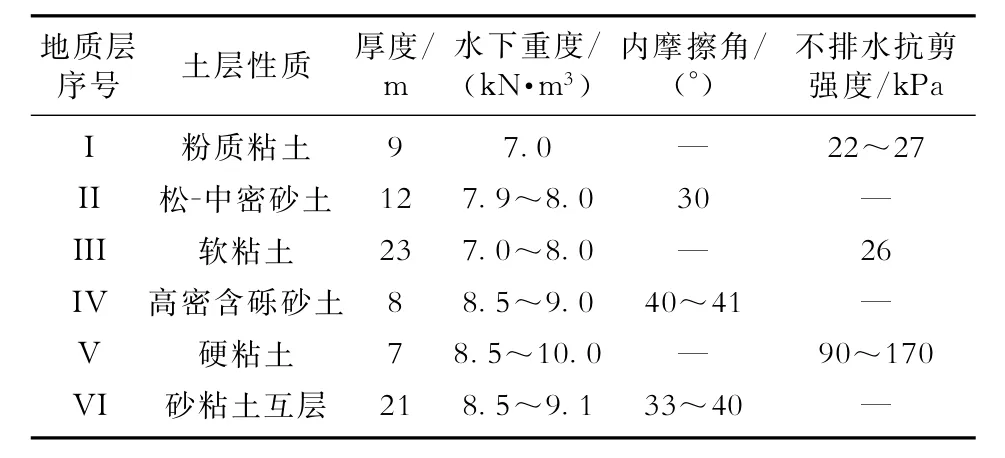
表1 南海某地区海床工程地质数据

3.2 初始应力场平衡

模拟井口的水平承载力必须用三维模型来进行分析,模拟井口的竖向承载力可以使用二维模型来进行分析。建立模型后通过施加边界条件与自重载荷,得到的模拟水平承载力模型与竖向承载力模型下的初始应力场平衡结果分别如图5、6所示。从图5、6可以看出,土体初始地应力场的位移都在10-4m左右,这说明地应力的平衡达到了预期的效果,可以进行后续的加载模拟。

图5 本文算例水平承载力模型地应力场平衡结果

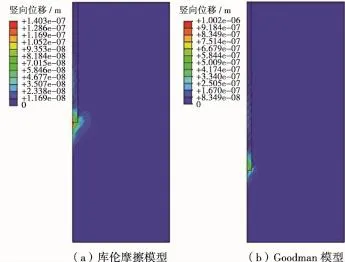
图6 本文算例竖向承载力模型地应力场平衡结果

3.3 导管横向承载力有限元模拟

分别用接触力学法与接触单元法编制相应的有限元计算程序,对喷射下入导管后导管在承受3×106N·m的顶部弯矩与1 MN的竖向力共同作用下的横向位移进行了模拟计算,其结果如图7所示。

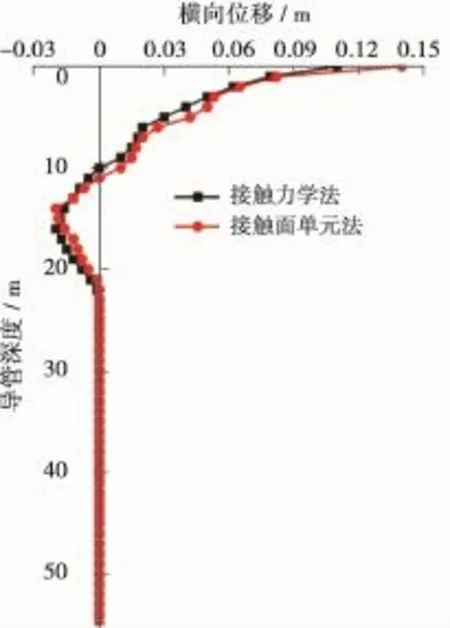
图7 本文算例用接触力学法和接触面单元法计算得到的导管横向位移(在承受3×106N·m的顶部弯矩与1 MN的竖向力共同作用下)

由图7可以看出,导管的横向位移较为严重的部分集中在导管上部较浅的一段距离(约为20m),在某深度以下导管几乎没有横向位移;由接触面单元法计算所得结果大于接触力学法模拟结果,这与2种计算方法采取的本构模型不同有关。因此,从井口稳定性角度出发,建议使用接触面单元法计算导管的横向位移,进行喷射下导管的有关设计工作。

由于使用接触面单元法计算结果大于接触力学法计算结果,为提高深水喷射下导管作业的安全系数,下面使用接触面单元法分析导管顶部作用力对其横向位移的影响。

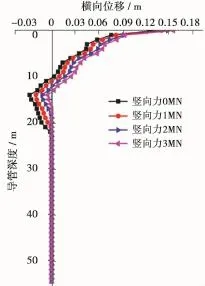
图8 本文算例不同竖向力对导管横向位移的影响

在导管受到顶部弯矩3×106N·m保持不变的情况下,导管在分别承受0、1、2、3 MN竖向载荷的情况下的横向位移模拟结果如图8所示。在导管顶部受到竖向力为1 MN保持不变的情况下,导管在分别承受1×106、2×106、3×106、4×106N·m顶部弯矩的情况下的横向位移模拟结果如图9所示。

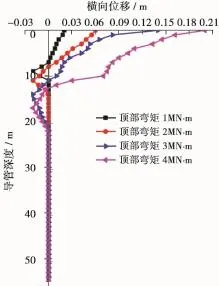
图9 本文算例不同顶部弯矩对导管横向位移的影响

从图8、9可以看出:在导管受到顶部弯矩不变的情况下,导管的横向位移随竖向力的增大而增大;在导管竖向力不变的情况下,导管横向位移随顶部弯矩的增大而增大。两者相比较而言,顶部弯矩对导管的横向位移影响更为显著。竖向力及顶部弯矩的大小受海浪流、水下井口、防喷器组、隔水管、张紧系统及底部连接球铰等因素的影响,所以合理确定张紧系统、正确计算海浪流作用力、及时控制钻井平台(船)的偏移对于水下井口的安全性至关重要。

3.4 导管竖向承载力有限元模拟

结合表1中的数据,根据式(2)、(3)计算所得导管极限承载力见表2。根据表2的计算结果,结合式(3)最终计算得到的导管允许承受的最大竖向载荷为8 721.7 kN。

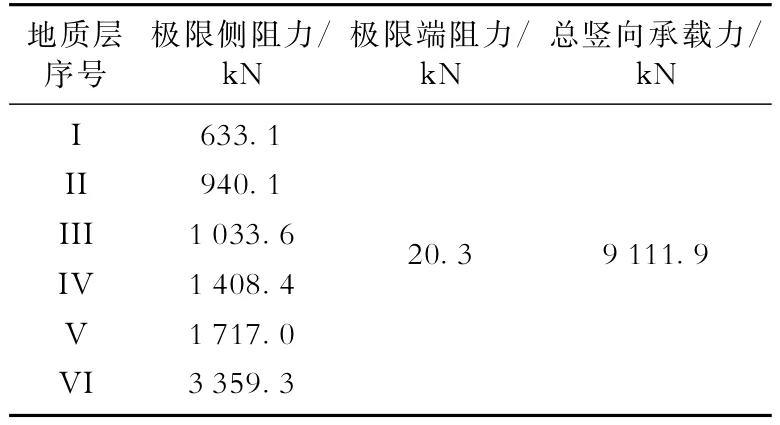
表2 本文算例导管竖向极限承载力理论计算结果

分别利用库伦摩擦模型与Goodman接触面单元模型,通过编制相应的有限元计算程序[16-18],对喷射下入72m导管后的竖向承载力进行了模拟计算,结果如图10所示。

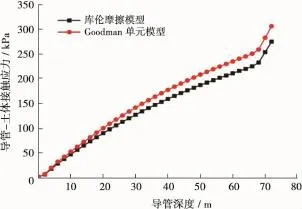
图10 本文算例用库伦摩擦模型和Goodman单元模型计算得到的桩土界面接触应力

得到管土接触界面的接触应力后可以通过式(6)计算导管侧壁的摩阻力:

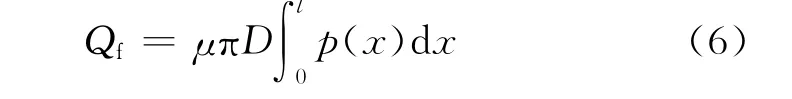
式(6)中:p(x)为管土界面接触应力随导管深度的变化,kPa;D为导管外径,m;μ为桩土界面切向摩擦系数。

根据式(6)计算得到的不同桩土接触界面模型导管竖向承载力如表3所示。

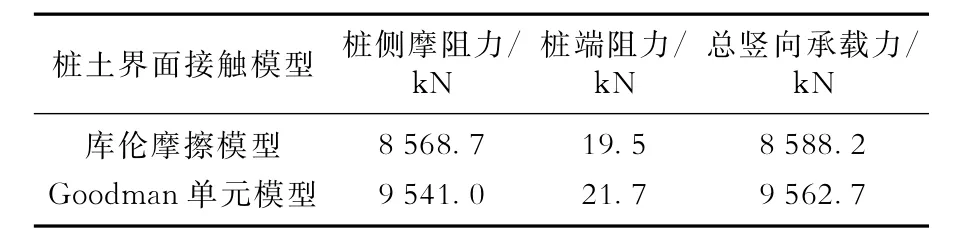
表3 本文算例导管竖向承载力有限元计算结果

由表3可以看出,由Goodman单元模型计算所得导管竖向承载力大于由库伦摩擦模型计算结果,并且在总的竖向承载力中桩侧摩阻力占绝大部分,桩端阻力对总竖向承载力的贡献很小。库伦摩擦模型、Goodman单元模型以及理论计算所得值对比情况如图11所示。

由图11可以看出,随着导管入泥深度的增加,其竖向承载力逐渐增大,不同计算模型下计算得到的导管竖向承载力不同,这与3种计算方法选取的本构模型不同有关。由Goodman单元模型计算所得导管竖向承载力大于由库伦摩擦模型计算所得结果,这种关系在图10中也得到了体现。本算例中,在浅部地层(33m)由库伦摩擦模型计算结果最小;在33～64m之间由理论模型计算所得结果最小;在64～72m之间由库伦摩擦模型计算所得结果最小。为提高水下井口的安全系数,建议在进行喷射下导管计算其竖向承载力时选取不同的模型进行计算,选取计算结果的最小值作为设计依据。

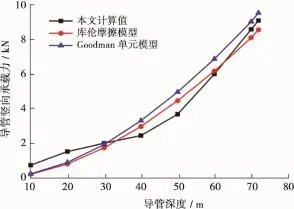
图11 本文算例不同计算模型下导管竖向承载力随桩深的变化

由于常用的喷射导管尺寸有φ914.4mm和φ762.0mm两种,假设喷射下入的导管深度均为72m,分别用上述3种方法计算所得导管竖向承载力随入泥深度的关系如图12所示。

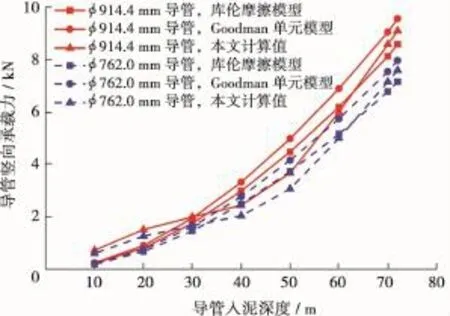
图12 本文算例导管尺寸对导管竖向承载力的影响

由图12可以看出,导管尺寸对导管竖向承载力有影响,导管尺寸越大其竖向承载力越大。但大尺寸导管意味着喷射下入的难度与时间增大,经济成本提升,因此在选择喷射下入导管尺寸时应综合考虑其竖向承载力与经济成本。

4 结论

1)建立了深水导管横向位移和竖向承载力的计算模型,考虑了初始地应力的影响,进行了有限元数值分析,结果表明采用接触面单元法计算所得导管横向位移大于接触力学法计算所得结果,采用Goodman模型计算得到的导管竖向承载力大于库伦摩擦模型计算结果。为了提高井口稳定性与水下井口安全系数,建议使用接触面单元法计算导管的横向位移,选取不同模型进行导管竖向承载力计算,并选取计算结果的最小值进行喷射下导管的有关设计工作。进行喷射下导管计算其竖向承载力时选取不同的模型进行计算,选取计算结果的最小值作为设计依据。

2)分析了导管顶部竖向力及弯矩对导管横向位移,以及导管尺寸对导管竖向承载力的影响规律,结果表明导管顶部竖向力及弯矩对导管横向位移均有影响,但顶部弯矩对横向位移的影响更为显著。此外,导管尺寸对导管竖向承载力也有影响,导管尺寸越大其竖向承载力越大,但大尺寸导管意味着喷射下入的难度与时间增大,经济成本会提高,因此在选择喷射下入导管尺寸时应综合考虑其竖向承载力与经济成本。

[1]BECK R D,JACKSON C W,HAMILTON T K.Reliable deepwaterstructural easing installation using controlled jetting[C]. SPE 22542,1991.

[2]PHILIPPE J.Innovative designmethod for deepwatersurface casings[C].SPE 77357,2002.

[3]孙友义,陈国明,畅元江.超深水隔水管悬挂动力分析与避台风策略探讨[J].中国海上油气,2009,24(2):29-32.

[4]许亮斌,蒋世全,畅元江,等.浮力块对深水钻井隔水管主要性能的影响[J].中国海上油气,2007,19(5):338-342.

[5]管志川,苏堪华,苏义脑.深水钻井导管和表层套管横向承载能力分析[J].石油学报,2009,2(30):286-290.

[6]李基伟.深水导管柱承载能力的研究[D].河北秦皇岛:燕山大学,2012.

[7]林天键.桩基础设计指南[M].北京:中国建筑工业出版社, 1999.

[8]高大钊.土力学与基础工程[M].北京:中国建筑工业出版社, 1998.

[9]American Petroleum Institute.API RP 2A-WSD-2000 Recommendedpractice forplanning,designing and constructing fixed offshoreplatforms-workingstress design[S].Washington D C:American Petroleum Institute,2000.

[10]李守德,俞洪良.Goodman接触面单元的修正与探讨[J].岩土力学与工程学报,2004,23(15):2628-2631.

[11]任艳荣,刘玉标,顾小芸.用ABAQUS软件处理管土相互作用中的接触面问题[J].力学与实践,2004(6):43-44.

[12]张嘎,张建民.土与结构接触面弹塑性损伤模型用于单桩与地基相互作用分析[J].工程力学,2006,23(2):72-77.

[13]雷晓燕,SWOBODA G,杜庆华.接触摩擦单元的理论及其应用[J].岩土工程学报,1994,16(3):23-32.

[14]段文峰,廖雄华,金菊顺.桩-土界面的数值模拟与单桩Q-S曲线的数值分析[J].哈尔滨建筑大学学报,2001,34(5):34-38.

[15]张明义,邓安福,干腾军.静力压桩数值模拟的位移贯入法[J].岩土力学,2003,4(1):113-117.

[16]张明义.静压桩连续贯入的模拟与承载力全过程研究[D].山东青岛:青岛理工大学,2010.

[18]代汝林,李忠芳,王姣.基于ABAQUS的初始地应力平衡方法研究[J].重庆工商大学学报:自然科学版,2012,29(2):76-81.

[19]付英军,姜伟,朱荣东.深水表层导管安装方法及风险控制技术研究[J].石油天然气学报:江汉石油学院学报,2011,33(6): 153-157.

[20]杨进,刘书杰,王平双,等.海上钻井隔水导管下入深度理论与控制技术[M].北京:石油工业出版社,2009.

Numerical analysis of bearing capacity of deep water conductor with consideration of different contract interfacemodels betweenpile andsoil

Wang Yanbin Gao Deli Fang Jun
(MOE Key Laboratory of Petroleum Engineering in China University of Petroleum,Beijing,102249)

It is important to use the reasonablepilesoil contactmodel to calculate the bearing capacity of deep water conductor.Theoreticalmodels to calculate the lateral displacement and its vertical bearing capacity have been established.Besides, taking the influence of initial In-situstress field into consideration,the lateral displacement and vertical bearing capacity of deep-water conductor have been calculated respectively by writing finite elementprograms for corresponding constitutivemodels with ABAQUS.The two differentmodels calculating lateral displacement are contactmechanicsmodel and contact elementmodel.The two differentmodels calculating vertical bearing capacity are coulomb frictionmodel and Goodman element contactmodel.The calculation resultsshow that the lateral displacement calculated by the contact elementmethod is greater than that calculated by contactmechanicsmethod,the vertical bearing capacity calculated by Goodmanmodel is greater than that calculated by the coulomb frictionmodel.Moreover,the influence of conductor top load and bendingmoment on its lateral displacement and the influence of conductorsize on its vertical ultimate bearing capacity are also analyzed.Themethod introduced in thispaper has a reference value for engineering design and control of conductor.

deep water drilling;conductor;pile andsoil contactmodel;lateral displacement;vertical bearing capacity;numerical analysis

2014-03-13

(编辑:孙丰成)

*国家自然科学基金创新研究群体项目(编号:51221003)部分研究成果。

王宴滨,男,中国石油大学(北京)在读博士研究生,主要研究方向为油气井力学与控制工程。地址:北京市昌平区府学路18号中国石油大学(北京)273信箱(邮编:102249)。