VTI介质各向异性叠前时间偏移方法*

井涌泉 樊鹏军 谭 卓 董建华 范廷恩 胡光义

(中海油研究总院)

VTI介质各向异性叠前时间偏移方法*

井涌泉 樊鹏军 谭 卓 董建华 范廷恩 胡光义

(中海油研究总院)

基于VTI介质的假设,通过结合单程波方程与VTI介质的时间偏移频散关系,发展了一种基于波动方程的VTI介质各向异性叠前时间偏移方法,给出了由均方根动校正速度与均方根各向异性参数确定的走时和幅值解析表达式。同时,综合分析速度与各向异性参数对CRP道集走时的影响,通过CRP道集内同相轴剩余动校时差的迭代拾取,实现了在偏移过程中偏移速度与各向异性参数的建模。理论模型试算和南海某深水区二维地震数据成像结果表明,应用VTI介质各向异性叠前时间偏移方法可以实现大角度倾斜界面更为准确的成像归位,同时能够保证剖面的能量聚焦效果。

各向异性参数;频散关系;VTI介质;叠前时间偏移

当地下介质构造比较复杂但速度横向变化不是很剧烈时,基于地下介质是各向同性的叠前时间偏移可以比较有效的对地下介质进行成像[1],目前这种方法已在国内得到广泛的研究与应用,并且获得了很好的应用效果。但是,最近的理论研究[2-3]、实验室观测[4]以及野外工作[5-9]都表明,大多数沉积岩均表现出了各向异性的特征,而且随着勘探规模的逐渐加大,大角度远偏移距的数据也显示出了非双曲形式走时特征(这主要是由速度在垂向上的不均匀性导致的各向异性而引起的)。因此,在各向异性介质条件下仍然使用常规的各向同性叠前时间偏移和速度分析方法,势必会导致成像精度不够,造成大倾角构造的反射层出现较大的横向归位误差,并最终影响地质解释。

一般而言,VTI介质(具有垂直对称轴的横向各向同性介质)是对地下介质各向异性一个很好的近似,因而研究VTI各向异性介质的叠前时间偏移成像理论和方法,考虑复杂构造情况下地震波传播的各向异性效应,实现对复杂构造准确的偏移成像归位,对于提高勘探成功率具有重要的现实意义。本文提出了一种基于相移法[10-12]、稳相点原理[13]和采用输入道成像方式[14]的VTI介质各向异性叠前时间偏移方法,给出了由介质均方根动校正速度和均方根各向异性参数计算单道数据走时和幅值的解析表达式。同时,通过对比分析各种基于P波资料反演速度及各向异性参数方法[15-17]的特点及应用条件,形成了一种以各向异性参数扫描为核心,根据CRP道集内大偏移距同相轴剩余动校时差拾取的偏移叠加速度与各向异性参数的建模流程。最后,以南海某深水区二维地震数据为例,分析了该方法的应用效果,同时验证了该方法的有效性。

1 VTI介质偏移脉冲响应

1.1 VTI介质基本参数

在只考虑P波的情况下,表征VTI介质的Thomsen参数有3个,即Vp0、ε、δ。其中Vp0为P波的垂向层速度,ε为XOZ平面上的P波的各向异性参数,δ为XOZ平面上的变异参数。

对于VTI介质,只需要求得各向异性介质的层动校正速度vnmo与非椭圆各向异性参数η这2个参数,就可以完全实现与时间有关的处理流程,如动校正、倾斜动校正、叠后时间偏移和叠前时间偏移。其中,各向异性介质的层动校正速度vnmo与变异参数δ的关系为

式(1)表明,层动校正速度只与δ有关,与ε无关。这说明,式(1)适用于不同强度的各向异性介质。

另外,令vh为P波水平方向速度,则有

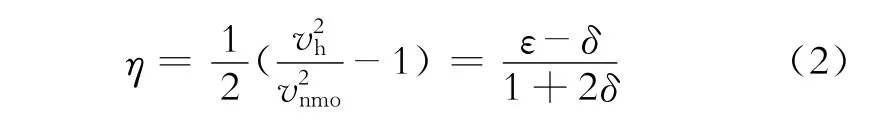
式(2)表明,非椭圆各向异性参数η与各向异性强度成正比,具有比P波水平方向速度vh更直观的地球物理意义。

1.2 VTI介质频散关系

时间域偏移频散关系式为

式(3)中:ω0是零偏移距角频率;ωm是偏移后的角频率;px、pz分别为地震波在水平x方向和垂直z方向上的射线参数;Vp0为地层速度。

在Tsvankin重新定义的VTI介质中,由Thomsen各向异性参数[4]表示的相速度表达式[3]为

VTI介质中,相速度同时也满足式(5)所示的关系式,即

将式(4)代入式(5),整理可得

对式(6)整理求解,并用层动校正速度vnmo与非椭圆各向异性参数η替换表示,则有

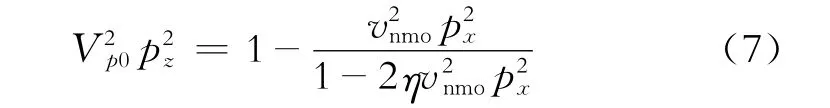
式(7)即为在只考虑P波的情况下关于Vp0、vnmo以及η的VTI介质的频散关系表达式。分析式(7)可以看出,当px=0时;当时,为最大值;当η=0时,该式退化为各向同性介质的频散关系。

1.3 走时和幅值计算

时间偏移算法的基本理论假设条件是假定地下介质是横向均匀的,因此,基于深度偏移的相移法研究VTI各向异性介质单炮正传和单道数据反传的走时及振幅的计算方法。在频率-波数域,VTI各向异性介质单炮和单道数据可统一看作空间脉冲函数,可用f(ω)表达,基于相移法,其沿深度方向延拓的相移算子P(kz,ω,Δz)可表示为

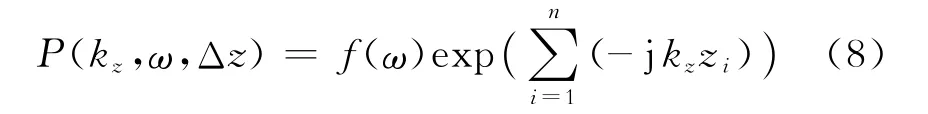
式(8)中:kz为垂直方向的波数;ω为地震波频率; Δz为深度延拓步长;zi为第i层深度。

用时间表示波场延拓步长,同时令z方向的射线参数pz=kz/ω,用单程波旅行时表达深度,则延拓到t深度时的波场为

式(9)中:ΔTi是各层的时间厚度;Tn为时间厚度; vi是各层介质垂向层速度。

对式(9)中的vipz用VTI介质频散关系式(7)进行替换,得到具有各向异性传播效应的相移表达式为

式(10)中的指数项可以近似表达为

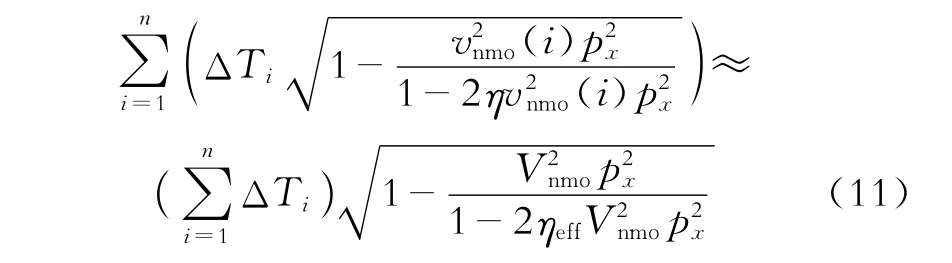
对式(11)两边做Taylor展开,通过求解,可得VTI各向异性叠前时间偏移所需要的2个偏移参数,即均方根动校正速度Vnmo和均方根各向异性参数ηeff。

由于px与频率无关,因此式(14)可用稳相点原理求得渐进解为

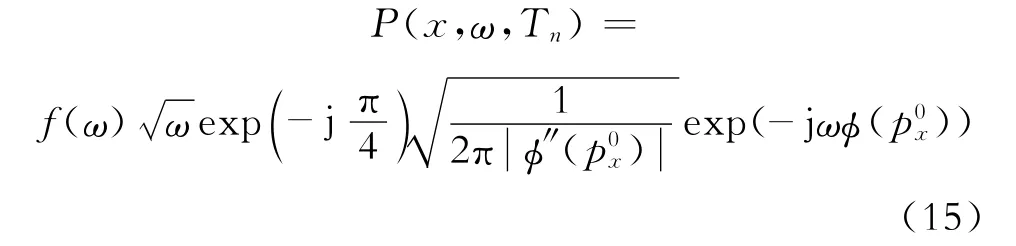
式(15)中:φ(px)=φ″(px)是φ(px)的二阶导数是φ′(px)的零点;即分别为地震波在VTI各向异性介质传播的走时t和幅值A。

理论研究表明,当频率大于2Hz时,式(15)是式(14)的很好近似,对于地震勘探而言,这是很容易就可以满足的,因此将式(15)作为VTI各向异性介质频率域空间波场的解析表达式。

1.4 单道脉冲响应计算

对于采用输入道成像方式的叠前时间偏移方法,单道地震数据的脉冲响应作为偏移的基础,其走时和幅值的计算精度直接决定了偏移的成像效果和精度。对于任一道地震数据,其震源与检波点坐标是已知的,对于地下某一拟成像CRP点,可由偏移孔径确定成像的范围;对于任一CRP点以及成像深度(旅行时),计算可以得到地震波由炮点至成像点正传播和成像点至接收点反传播的走时及幅值,分别记为ts、tr、As、Ar,这样就可以利用波动方程深度偏移的反褶积成像条件成像[18]。

设震源是一时间脉冲函数,则二维情况下表达式为

积分中的前3项可看作是该道数据半导数的傅里叶反变换,记其在时间域为Fh(t),则式(16)可进一步简化为

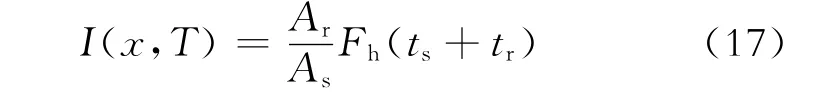
在做半导数的数据中通过插值拾取(ts+tr)时刻的值,然后乘上由幅值确定的权系数,这样就完成了任一单道数据在某一成像点的成像过程,由式(17)可知计算结果是一组半椭圆。

1.5 模型试算

图1为根据式(16)计算的单道偏移脉冲响应。其中,图1a为各向同性介质的偏移脉冲响应,偏移速度Vrms=2 000m/s;图1b为各向异性介质的偏移脉冲响应,偏移速度Vrms=2 000m/s,各向异性参数η=0.25。对比可以看出,对由浅层到深层的4个偏移脉冲响应而言,各向同性偏移的最大时间深度和各向异性偏移的最大时间深度是一样的,因为在垂直方向上的传播速度都为2 000m/s。但是,在水平方向的展布范围显著不同,对比浅层脉冲响应(0.8s处脉冲响应),高角度部分脉冲响应与x= 4 000m和x=6 000m的坐标轴渐进距离显然不同,各向同性偏移结果距离两坐标轴较远,而各向异性偏移结果更接近两坐标轴。这表明,偏移过程中考虑介质各向异性时,高角度构造进行成像时各向异性偏移结果相比于各向同性偏移结果向上倾方向移动,构造倾角变大,更接近于实际构造倾角,成像更准确。同样,对于中、深部脉冲响应的大角度部分,也表现出类似的特征。因此,各向异性时间偏移的走时与各向同性时间偏移的走时存在显著差别。

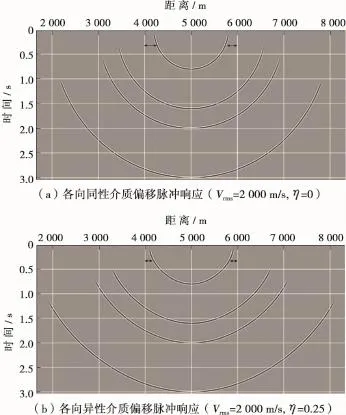
图1 单道偏移脉冲响应对比

2 VTI介质叠前时间偏移及参数建模流程

对经过静校正等处理的叠前地震数据进行VTI各向异性叠前时间偏移处理,大致可以分为如下几个步骤(图2):

图2 VTI介质叠前时间偏移及参数建模流程

1)对原始记录进行传统的速度分析,拾取叠加速度并对每个时间深度计算其慢度平均值,以此作为偏移处理的初始速度;

2)偏移速度主要控制近偏移距小角度数据的走时,因此对原始数据进行各向同性叠前时间偏移处理,得到CRP道集,用偏移速度对其进行反动校(反NMO),并抽取偏移距与深度比小于1的范围内的数据,进行传统的速度分析得到较为准确的均方根速度场Vnmo;

3)各向异性参数主要控制远偏移距大角度数据的走时,因此由获得的均方根速度场与各向异性参数ηeff对CRP道集(包括近偏移距及远偏移距)进行各向异性动校正,采取扫描分析的形式,直到同相轴被校正平直为止,所对应的各向异性参数ηeff即为该CRP道集这一时间深度的各向异性参数,这样便可以得到各向异性参数场;

4)对均方根速度场以及各向异性参数场进行平滑处理,作为VTI各向异性叠前时间偏移的2个参数;

5)对原始数据进行VTI各向异性叠前时间偏移处理,获得CRP道集;

6)将CRP道集校平叠加,得到最终的偏移结果。

3 应用效果分析

为了验证本文VTI介质各向异性叠前时间偏移方法的应用效果,选取我国南海某深水区二维地震数据进行偏移成像试验。该地震数据共3 281炮,单炮数据180道,最小偏移距206m,最大偏移距4 985m,通过各向同性叠前时间偏移处理,发现在CRP道集内的不同深度大偏移距同相轴均存在向上弯曲归位不准确等问题,初步分析认为是由各向异性或垂向不均匀性所致。

应用本文提出的VTI介质各向异性叠前时间偏移方法对该地震数据进行各向异性参数反演及叠前时间偏移成像处理。首先,对近偏移距数据进行偏移成像,建立了比较准确的均方根速度场(图3);然后,使用相同的速度做反动校正的CRP道集可等效为CDP道集,对反动校正后的CRP道集进行各向异性动校正扫描(图4),确定了不同时间深度同相轴较为平直时的ηeff(其他时刻则通过两点插值),这样就建立了该CRP道集的ηeff曲线(图4中白色曲线)。基于以上流程,即可实现各CRP道集的各向异性速度分析,并最终建立偏移均方根速度场Vnmo(图3)和各向异性参数场ηeff(图5)。

图3 南海某深水区二维地震数据均方根速度场

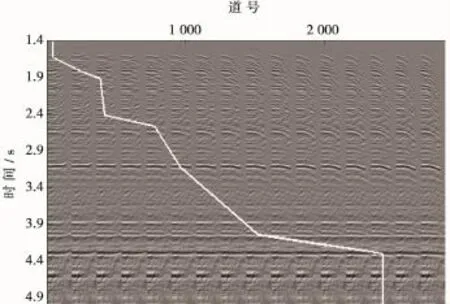
图4 对反动校正后的CRP道集进行各向异性动校正扫描结果

图5 南海某深水区二维地震数据均方根各向异性参数场

在此基础上便可以对该地震数据进行各向异性叠前时间偏移处理。图6a为该地震数据各向同性叠前时间偏移后的CRP道集,最大偏移距近5 km,可以看到道集内同相轴在小角度近偏移距范围内非常平直,而在大角度远偏移距部分由浅至深同相轴出现了不同程度的向上弯曲,这主要是由于介质的各向异性以及垂向不均匀性导致的。为了能够在叠加剖面上有比较好的聚焦成像效果,对向上弯曲的这部分数据采取适当的切除,从而避免了不必要的人为切除浪费。图6b为该地震数据各向异性叠前时间偏移后的CRP道集,可以很明显的看到,道集内的同相轴要比各向同性叠前时间偏移的同相轴有很大的改善,同相轴平直了很多,由近偏移距到远偏移距基本都是平直的。

图6 南海某深水区二维地震数据叠前时间偏移CRP道集对比

图7为该地震数据各向同性叠前时间偏移与各向异性叠前时间偏移的叠加剖面。对比A处的近水平界面(图8),由于在叠加过程中对大偏移距数据实现了同相叠加,各向异性叠前时间偏移剖面的同相轴能量要更强一些,同时连续性也更好。对比B处的局部构造成像(图9),白色线为各向异性叠前时间偏移倾斜界面的标识线,在各向异性叠前时间偏移剖面上(图9b)可以看到大倾角倾斜界面向上倾方向发生了明显的移动,这与脉冲响应实验分析是一致的。

综合以上对比分析结果可以看出,应用本文提出的VTI介质各向异性叠前时间偏移方法,在叠加剖面上实现了大角度倾斜界面更为准确的成像归位,同时保证了剖面的能量聚焦效果。

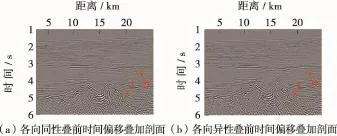
图7 南海某深水区二维地震数据叠前时间偏移成像对比

图8 南海某深水区二维地震数据偏移成像聚焦能力对比

图9 南海某深水区二维地震数据大倾角构造成像对比

4 结论

1)提出了一种VTI介质各向异性叠前时间偏移方法。该方法通过提高高角度、大偏移距走时的精度,实现了CRP道集内大偏移距同相轴的同相叠加,增强了叠加剖面的聚焦能力,提高了大倾角构造成像的精度,从而避免了人为切除浪费等问题。同时,给出了由反射P波地震数据驱动建立均方根各向异性参数场的流程,实现了利用VTI各向异性动校正扫描建立各向异性参数场的目标,避免了由于大偏移距数据不足造成的各向异性参数反演精度不高等问题。

2)通过实际海上二维地震数据偏移成像试验,验证了本文方法的有效性,为类似复杂构造地震资料偏移成像处理工作提供了借鉴。

[1]HUBRAL P.Timemigration:some ray theoretical aspects[J]. Geophysical Prospecting,1977,25:738-745.

[2]LEVIN F K.Seismic velocities in transversely isotropicmedia [J].Geophysics,1979,44(5):918-936.

[3]TSVANKIN I.P-wavesignatures and notation for transversely isotropicmedia:an overview[J].Geophysics,1996,61(2): 467-483.

[4]THOMESEN L.Weak elastic anisotropy[J].Geophysics,1986, 51(6):1954-1966.

[5]BALL G.Estimation of anisotropy and anisotropic 3Dprestack depthmigration,offshore Zaire[J].Geophysics,1995, 60(5):1495-1513.

[6]羊屋三维处理解释一体化方法研究组.纵波VTI介质理论与应用研究[J].石油地球物理勘探,2002,37(3):267-275.

[7]凌云研究小组.宽方位角地震勘探应用研究[J].石油地球物理勘探,2003,38(4):350-357.

[8]李建荣,王磊,王赟.开发地震的几个问题初探[J].石油物探, 2003,42(2):279-284.

[9]李绪宣,张树林.利用多波地震资料初步探讨地下介质各向异性[J].中国海上油气(地质),1999,13(5):387-390.

[10]GAZDAG J.Wave equationmigration with thephase-shiftmethod[J].Geophysics,1978,43:1342-1351.

[11]刘礼农,高红伟,刘洪,等.三维VTI介质中波动方程深度偏移的最优分裂Fourier方法[J].地球物理学报,2005,48(2): 406-414.

[12]刘礼农,陈小宏,张剑锋,等.轴对称各向异性介质波动方程深度偏移的对称非平稳相移方法[J].地球物理学报,2007,50(1): 277-284.

[13]BLEISTEIN N,CHOHEN J K,STOCKWELL J W.Mathematics ofmultidimensionalseismic imaging,migration and inversion[M].New York:Springer,2001.

[14]TYGEL M,SCHLEICHER J,HUBRAL P.A unified approach to 3Dseismic imaging,migration and reflection imaging[M]. New York:Geophysics,1996,61(3):759-775.

[15]ALKHALIFAHT,TSVANKIN I.Velocity analysis for transversely isotropicmedia[J].Geophysics,1995,60(5):1550-1566.

[16]TARIQ A.Velocity analysis using nonhyperbolicmoveout in transversely isotropicmedia[J].Geophysics,1997,62(6): 1839-1854.

[17]SILIQI R,MEUR D L,GAMAR F,et al.High-densitymoveoutparameter fields V andη[J].SEG Technical Program Expanded Abstracts,2003:26-31.

[18]ZHANG J F,WAPENAAR K.High-resolution depth imaging withsparseness-constrained inversion[J].Geophysical Prospecting,2006,54:49-62.

Amethod of anisotropicprestack timemigration in VTImedia

Jing Yongquan Fan Pengjun Tan Zhuo Dong Jianhua Fan TingenHu Guangyi
(CNOOC Research Institute,Beijing,100027)

On an assumption of VTI(vertical transverse isotropy)media,a wave-equation-basedmethod of anisotropicprestack timemigration in VTImedia was developed by including the dispersion relation between one-way wave equation and timemigration in VTImedia,and the analytical expressions of travel time and amplitude were determined by the dynamic correction velocity of rootmeansquare and the anisotropicparameter of rootmeansquare.Meanwhile,the impacts of velocity and anisotropicparameter on CRP-gather travel time were comprehensively analyzed,and buildingmodels formigration velocity and anisotropicparameter was realized duringmigration by the iterativepickup of residual dynamic correctionmoveout in the events within CRP gathers.A testing of theoreticalmodel calculation and the 2Dseismic imaging in a deep water area,South China Sea,haveshown that applying themethod of anisotropicprestack timemigration in VTImedia can result inmore accurate imaging ofsteep angled reflections and ensure energy focusing onseismicsections.

anisotropicparameters;dispersion relation;VTImedia;prestack timemigration

2013-07-08改回日期:2014-04-10

(编辑:冯 娜)

*“十二五”国家科技重大专项“海上开发地震关键技术及应用研究(编号:2011ZX05024-001)”部分研究成果。

井涌泉,男,工程师,2009年毕业于中国科学院地质与地球物理研究所,获固体地球物理学博士学位,现主要从事油田开发地震研究工作。地址:北京市东城区东直门外小街6号海油大厦512室(邮编:100027)。E-mail:jingyq@cnooc.com.cn。