响应变量缺失时偏线性测量误差模型的变量选择

黄 彬,杨凌霞,徐修友

(北京化工大学理学院,北京 100029)

变量选择是回归分析中的一个重要问题．当面对高维协变量集合时,选择对响应变量具有显著解释能力的协变量子集,对于简化模型，提高模型的解释能力十分重要．一些基于惩罚的变量选择方法,如LASSO(least absolute shrinkage and selection operator)[1],SCAD(smoothly clipped absolute deviation)[2],ALASSO(adaptive LASSO)[3]通过将部分回归系数收缩至零,有效地选择出重要变量并很好地估计模型参数,同时基于SCAD和ALASSO的估计具有渐进正态性和先知性(Oracle性质[2])．另外,Ueki[4]提出了STEE(smooth-threshold estimating equations)方法进行变量选择,它的优点是易于实现,不用求解凸优化问题．

偏线性模型是一种十分灵活的半参数模型,对于该模型及其推广模型的参数估计和变量选择已经有了广泛的研究[5-13]．然而,在响应变量缺失且协变量包含测量误差情况下,一个重要的问题是如何选择模型的重要变量,这个问题在文献中还没有被提及．本文主要研究偏线性模型在协变量包含测量误差且响应变量有缺失时的估计和变量选择问题．

我们将利用半参数回归替代方法[11]来处理缺失的响应变量．基于SCAD惩罚最小二乘和STEE,对偏线性模型的参数部分提出两种变量选择方法．通过选择合适的调整参数,且在一定的正则条件下,可以证明这两种变量选择方法具有渐进正态性和先知性．数值模拟研究显示,SCAD比STEE在估计精度和正确拟合模型方面更优,而STEE因不用求解凸优化问题而易于实现.

1 方 法

1.1 响应变量缺失时偏线性测量误差模型的估计

考虑偏线性模型

Y=XTβ+g(T)+ε,

(1)

这里X=(X1,…,Xp)T是p-维协变量向量,β是未知参数向量．为避免“维数灾难”,T是取值于[0,1]的标量协变量,函数g(·)是[0,1]上的未知函数,ε为随机误差,且E(ε|X,T)=0．令β0=(β01,…,β0p)T是β的真值．假设真实模型有一个稀疏形式,即β0的一些分量是0,令A0={j:β0j≠0}为重要变量下标集合．由于X包含测量误差,我们观测到W

W=X+U,

(2)

这里U是p-维测量误差,且均值为0,协方差阵为ΣUU．令δ是响应变量是否缺失的标志,即δ=1表示Y被观测到,δ=0表示Y缺失．假设选择概率

π(x,t)=P(δ=1|X=x,T=t,Y=y)=

P(δ=1|X=x,T=t)．

(3)

注意,因为X不能被直接观测到,所以这种缺失机制不是MAR(missing at ramdom)．进一步,假设U独立于(X,T,Y,δ),且ΣUU已知．若ΣUU未知,可由部分重复样本进行估计[5]．令{(Wi,Ti,Yi,δi),i=1,…,n}是来自模型(1)～(3)的随机样本,本文的目标是识别重要变量下标集合A0,并得到对应回归系数的相合估计．

为了处理模型中的缺失响应变量,Wang等[11]提出了基于插补、半参数回归替代方法来估计β和g(·)．Yang等[13]利用插补方法处理缺失的响应变量,同时考虑了协变量包含测量误差的情况．为了简单起见,我们应用半参数回归替代方法来处理缺失的响应变量．在本文缺失机制的假设下,可以证明所提出的估计与Yang等[13]提出的估计有相同的渐近方差．

注意δY=δXTβ+δg(T)+δε,定义

由假设,有

g(t)=g2,c(t)-g1,c(t)Tβ．

类似于Yang等[13],可以得到下面的两步估计．首先,利用完全观测数据得到β的初始估计

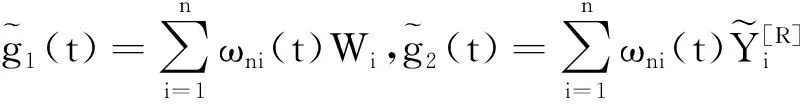
(4)

(5)

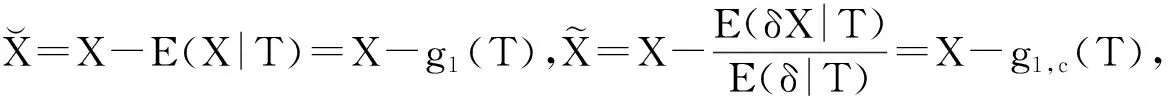
E[δ{(UUT-ΣUU)β}⊗2]．

同时假设模型(1)～(3)满足如下条件：

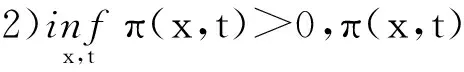
3)K(·)和M(·)为具有有界支撑的二阶有界核函数．

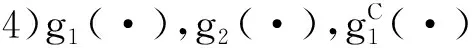
5)T的密度函数fT(t)存在且直到二阶导数都有界,满足

文献[11,13]中也有类似的条件．

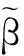
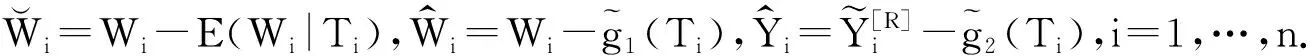
(6)

类似于文献[11]和文献[13]的证明,可得:

(7)

从而定理1得证．

1.2 基于SCAD惩罚最小二乘的变量选择

为同时选择重要变量并估计未知回归参数,Fan等[2]提出了一个基于SCAD惩罚似然的变量选择方法,且证明了当选择合适的调整参数时,SCAD惩罚似然估计与先知估计等效．我们应用SCAD惩罚对偏线性模型进行变量选择．

沿袭Fan等[2]方法,惩罚最小二乘定义为

(8)

其中pλj(·)是SCAD惩罚函数,λj是调整参数．注意对所有的j,pλj(·)中的λj不必相同．为了简单起见,我们假设β的所有分量的惩罚相同,且将pλj(·)写为pλ(·)．惩罚函数pλ(·)定义为

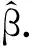
利用BIC准则[15]选择调整参数,通过极小化

BIC(λ)=logRSSλ+e(λ)log(n)/n,

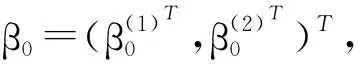
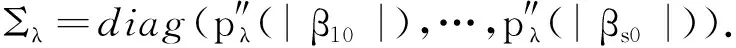
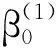
证明令αn=n-1/2+an,只需证对任意ε>0,存在一个大的常数M,使得

(9)

定义

且

注意pλ(0)=0和pλ(|β|)≥0对任意β成立,因此

LP(β0+αnu)-LP(β0)≥Dn1+Dn2.

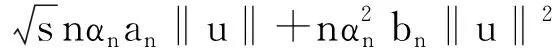
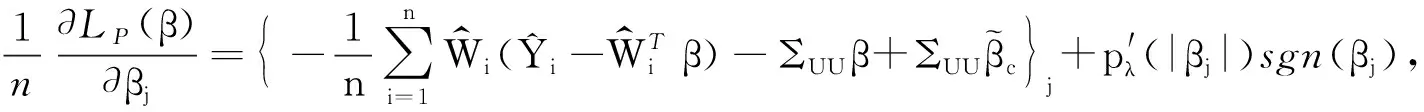
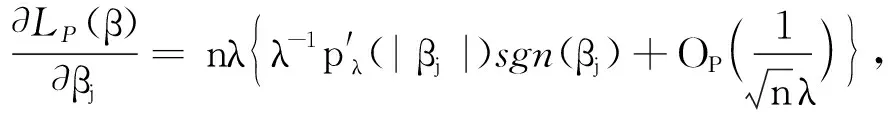
进一步,由泰勒展开,

类似于定理1的证明,可以得到

且

由Slutsky定理

1.3 基于STEE的变量选择

Ueki[4]提出了STEE变量选择方法,它通过自动将不显著的参数设置为0的方法,将对应的变量从模型中删除,且其估计具有先知性质．该方法的优点是易于实现,不需要求解凸优化问题即可得到估计．本节,我们应用这个方法对偏线性模型进行变量选择．

沿袭Ueki[4],利用估计方程(10),可以同时实现变量选择和参数估计,

(10)

其中

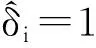
定理4在1)～7)下,对于任意正数λ和γ,使得当n→∞时,若n1/2λ→0和n(1+γ)/2λ→∞,则有

(i) 变量选择相合性,即P(A=A0)→1;

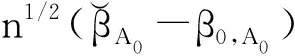
我们使用BIC-型准则[7]来选择调整参数,通过极小化

表1 数值模拟结果

2 数值模拟

本节,我们采用数值模拟的方法来进一步研究所提出的变量选择方法的有限样本性质．考虑模型

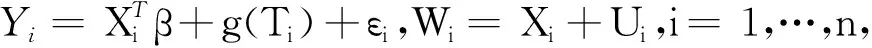
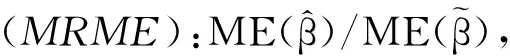
从表1可以看出,本文所提出的方法都显著地降低了模型复杂度．同时,SCAD估计在估计的精度和正确拟合模型方面,比STEE估计更好．SCAD估计的MRME非常接近于先知估计的MRME．而STEE估计由于不用求解凸优化问题而更易于实现．

[1] Tibshirani R.Regression shrinkage and selection via the lasso[J]．Journal of the Royal Statistical Society,Series B:Methodological,1996,58(1):267-288.

[2] Fan J,Li R.Variable selection via nonconcave penalized likelihood and its oracle property[J]．Journal of the American Statistical Association,2001,96:1348-1360.

[3] Zou H.The adaptive lasso and its oracle properties[J]．Journal of the American Statistical Association,2006,101(476):1418-1429.

[4] Ueki M.A note on automatic variable selection using smooth-threshold estimating equations[J]．Biometrika,2009,96(4):1005-1011.

[5] Liang H,Hardle W,Carroll R J.Estimation in a semiparametric partially linear errors-in-variables model[J]．The Annals of Statistics,1999,27:1519-1535.

[6] You J,Chen G.Estimation of a semiparametric varying-coefficient partially linear errors-in-variables model[J]．Journal of Multivariate Analysis,1996,97:324-341.

[7] Liang H,Li R.Variable selection for partially linear models with measurement errors[J]．Journal of the American Statistical Association,2009,104:234-248.

[8] Zhao P,Xue L.Variable selection for semiparametric varying coefficient partially linear errors-in-variables models[J]．Journal of Multivariate Analysis,2010,101:1872-1883.

[9] Wang H,Zou G,Wan A.Adaptive LASSO for varying-coefficient partially linear measurement error models[J]．Journal of Statistical Planning and Inference,2013,143:40-54.

[10] Wang Q H,Lindon O,Hardel W.Semiparametric regression analysis with missing response at random[J]．Journal of the American Statistical Association,2004,99:334-345.

[11] Wang Q H,Sun Z H.Estimation in partially linear models with missing responses at random[J]．Journal of Multivariate Analysis,2007,98:1470-1493.

[12] Liang H,Wang S,Carroll R.Partially linear models with missing response variables and error-prone covariates[J]．Biometrika,2007,94(1):185-198.

[13] Yang Y,Xue L,Cheng W.Two-step estimators in partial linear models with missing response variables and error-prone covariates[J]．Journal of Systems Science and Complexity,2011,24:1165-1182.

[14] Hunter D,Li R.Variable selection using MM algorithm[J]．The Annals of Statistics,2005,33:1617-1642.

[15] Wang H,Li R,Tsai C.Tuning parameter selectors for the smoothly clipped absolute deviation method[J]．Biometrika,2008,94:553-568.