空间分数阶Klein-Gordon方程的一种有效数值算法
2014-08-06周晓军
周 晓 军
(厦门大学数学科学学院,福建 厦门 361005)
分数阶微分方程已经被广泛应用于自然科学的各个领域,并逐渐成为一个活跃的研究领域.分数阶微分算子与整数阶微分算子不同,它具有非局部性,从而非常适合用来刻画现实生活中具有记忆和遗传特性的材料.譬如:分形和多孔介质中的弥散[1-2],电容理论[3],电解化学[4],生物系统中的电导[5],黏弹性系统量子力学[6-7],混沌同步[8]等等.然而,在这一领域还有许多未解决的问题,分数阶微分方程解的物理意义还没有确切的解释.尽管如此,这一新的领域仍然是科学工作者广泛关注的焦点.我们知道,大多数分数阶微分方程是没有准确解的,即使有解,多半也是级数表示,非常不便于实际应用,因此,设计有效稳定的数值算法求解分数阶微分方程是迫切需要的.目前,分数阶微分方程的数值解法主要有变分迭代法[9]、同伦摄动法[10-11]、Adomian分解法[12]、同伦分析法[13]、谱方法[14-15]等等.
Klein-Gordon方程是相对论量子力学和量子场论中的最基本方程,它是薛定谔方程的相对论形式,用于描述自旋为0的粒子,它是物理学中提出的一类非常重要的非线性发展方程,在数学物理、固态物理、非线性光学、量子场论[16]等领域有着极其重要的地位.关于它的理论和数值研究不断呈现,Li等[17]针对非线性Klein-Gordon方程,提出了一种保结构的有限差分格式,即原问题离散后,离散格式仍然保有连续问题的能量守恒性质.Bao等[18]对非相对论极限状态下Klein-Gordon方程的数值算法做了详尽分析和比较.
众所周知,逼近论中常用正交多项式作为一组基底来表示微分方程的解.Legendre多项式在数值计算中被广泛采用,陈一鸣等[19]运用Legendre 多项式求解变系数的分数阶Fredholm积分微分方程.本文将用移位Legendre正交多项式来构造分数阶Klein-Gordon方程的有效数值算法,我们在时间方向用有限差分格式,空间用移位Legendre正交多项式来逼近,并给出了算法的矩阵表示,便于计算机编程实现,将该算法用于线性和非线性的空间分数阶Klein-Gordon方程求解中.数值结果证实了所提出的算法是有效可行的.
1 问题描述及一些记号
空间分数阶Klein-Gordon方程为:
(x,t)∈(0,1)×(0,T),
(1)
初始条件为:
u(x,0)=φ0(x),ut(x,0)=φ1(x),
(2)
边界条件为:
u(0,t)=φ0(t),u(1,t)=φ1(t),
(3)
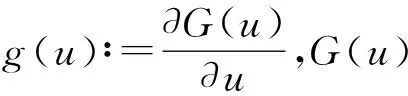
其中m是不小于α的最小整数,记为m=α.Dm是m阶经典导数,Iμ是Riemann-Liouville积分算子,定义如下:
由Caputo分数阶导数的定义立即得到:
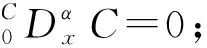
当α>0,λ≥0时,有[20]
(4)
从纯粹数学角度来看,Riemann-Liouville导数比Caputo导数更受欢迎,但在工程和数值计算上,在处理具体的物理问题时,Caputo导数只需给出在初始条件下的经典导数的值,这样导数就有明确的物理意义,然而,Riemann-Liouville导数需给出未知解在初始条件下的一些分数阶导数的具体值,分数阶导数可能没有合适的物理意义,因此,人们更愿意采用Caputo导数.且由两者的关系知道,在齐次条件下,Caputo导数和Riemann-Liouville导数是等价的.
2 移位Legendre多项式及其分数阶导数
众所周知,Legendre多项式,记为{Ln(z)},z∈[-1,1],是由勒让德方程的通解推导出来的,Ln(z)满足以下的奇异Sturm-Liouville方程
1)Ln(z)=0,z∈[-1,1].
关于Legendre多项式的递归关系是
L0(z)=1,
L1(z)=z,
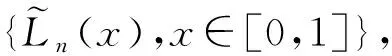
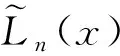
(5)
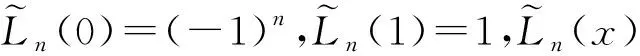
(6)
(7)
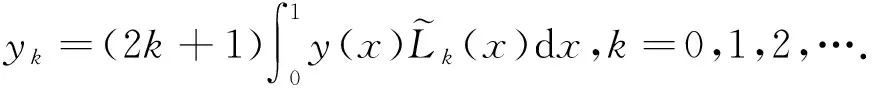
(8)
下面的定理给出了yN(x)的α阶Caputo分数阶导数的计算公式.
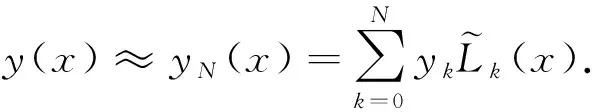
(9)
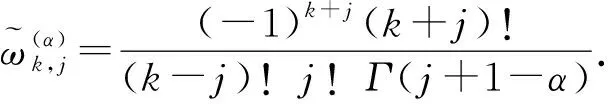
证明由Caputo分数阶导数的定义可知,它是一个线性算子,因此有
(10)
由式(4),易知,
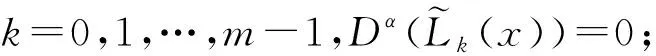
当k=m,…,N,
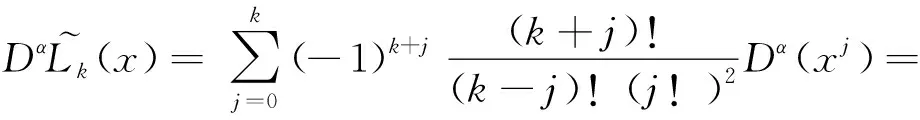
代入式(10)即得要证明的结果.
3 数值格式
问题(1)中,由于1<α<2,故m=α=2.为了构造方程的数值格式,首先逼近u(x,t)为
(11)
将式(11)代入式(1),并应用定理1,得到
g(uN(x,t))=f(x,t),
(12)
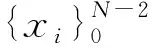
g(uN(xi,t))=f(xi,t),
i=0,1,…,N-2.
(13)
将式(11)代入式(3)得到
(14)
式(13)和(14)构成了N+1维常微分方程组,未知量为u0(t),u1(t),…,uN(t).
pmk=
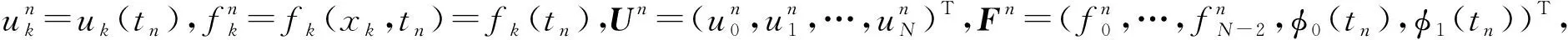
f(xi,t),i=0,1,…,N-2,n=1,2,…,M.
将上式与式(14)联立,写为矩阵形式是
P(Un+1-2Un+Un-1)-QUn+1+
g(PUn+1)=Fn+1.
(15)
注意:这里的g(PUn+1)是将函数g作用到向量PUn+1的每个元素上.
下面计算初始值U0,U1.由式(11)知
那么由正交性质(6)有
k=0,1,…,N.
(16)
又因为
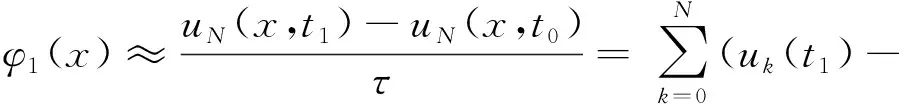
整理上式,并再一次由正交性质(6)得到
k=0,1,…,N,
(17)
那么由(16)、(17),再通过式(15)就能够求出U2,U3,…,UM.
特别地,(i) 取N=3,g(u)=u时,有
P=
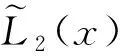
P(Un+1-2Un+Un-1)-QUn+1+PUn+1=Fn+1.
即
(2P-Q)Un+1=2PUn-PUn-1+Fn+1.
(18)
利用初始值U0,U1,通过式(18)容易求出U2,U3,…,UM.
(ii) 取N=3,g(u)=u3时,有
P(Un+1-2Un+Un-1)-QUn+1+
(PUn+1)3=Fn+1.
(19)
这是一个非线性的方程组,可以通过Newton迭代法来进行求解.
4 数值算例
首先,我们来看看分数阶Klein-Gordon方程与整数阶Klein-Gordon方程解之间的关系:
例1 考虑整数阶Klein-Gordon方程:
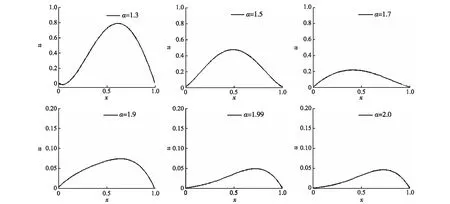
图1 T=1,α=1.3,1.5,1.7,1.9,1.99,2,Δt=10-5,N=4时的解Fig.1 The solutions of (20) for T=1,α=1.3,1.5,1.7,1.9,1.99,2,Δt=10-5,N=4
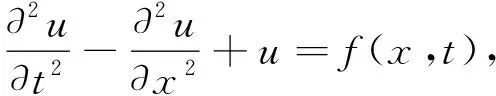
(x,t)∈(0,1)×(0,1),
(20)
其中f(x,t)=-2x(x3-x2-6x+3)e-t,精确解为:u(x,t)=x3(1-x)e-t.
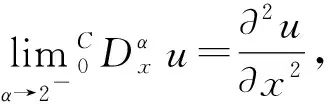
接下来,为了测试算法的有效性,用提出的数值格式(15)求解分数阶Klein-Gordon方程.
例2 线性分数阶Klein-Gordon方程
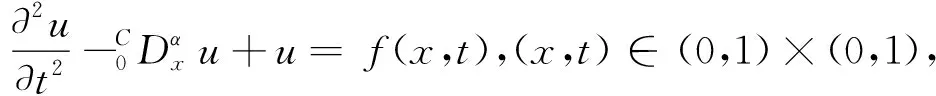
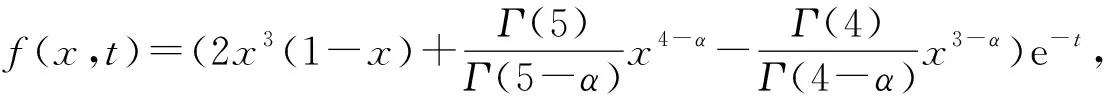
u(x,t)=x3(1-x)e-t.
为了观察解的精度,图2给出了数值解与它的精确解的对比,从图中可以看出采用本文数值算法求得的数值解较好地拟合了精确解,数值算例进一步验证了文中所给方法的可行性与有效性.
我们计算误差error=‖u(x,T)-uN(x,T)‖L2随着多项式次数变化的情况,见表1.我们取时间步长为Δt=10-5,当多项式次数由3变为4时,误差变化是极快的,在这里,由于时间仅仅是一阶逼近,所以多项式继续变化时,解的误差也不会继续缩小,这是符合实际情况的.值得指出的是,这里仅用4次正交多项式就能达到比较高的精度,说明数值格式是有效可行的.表2示出了固定多项式阶数为N=4时,不同的时间步长下误差的变化情况,从所列结果可以看出,误差随着时间步长的减小而急剧变小,说明算法是收敛的.
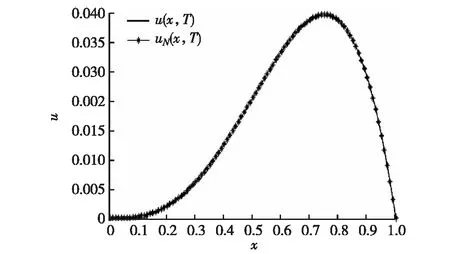
图2 T=1,α=1.2,Δt=10-5,N=4时数值解 与准确解的比较Fig.2 The compare of numerical and exact solution for T=1,α=1.2,Δt=10-5,N=4.
例3 非线性分数阶Klein-Gordon方程
(0,1)×(0,1),
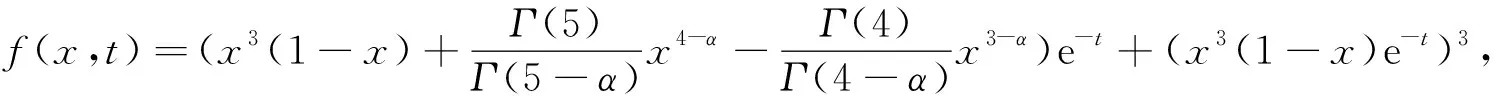

表2 T=1,Δt=10-1,10-2,10-3,10-4,10-5, α=1.2,1.5,1.8,N=4时的L2误差Tab.2 The L2 error to example 2 at T=1 for different α and Δt with N=4
为了进一步测试算法的可靠性,我们对非线性分数阶Klein-Gordon方程利用提出的数值格式作了测试.由于问题是非线性的,计算时间较长,所以数值结果中的时间步长只取到Δt=10-4,结果见表 3和表 4.

表3 T=1,Δt=10-4,α=1.2,1.5,1.8,N=3,4时的L2误差Tab.3 The L2 error to example 3 at T=1 for different α and N with Δt=10-4

表4 T=1,Δt=10-1,10-2, 10-3,10-4,α=1.2,1.5,1.8,N=4时的L2误差Tab.4 The L2 error to example 3 at T=1 for different α and Δt with N=4
5 结 论
本文利用Caputo分数阶导数的特点以及正交多项式的良好性质,提出了时间用有限差分,空间用移位Legendre正交多项式来逼近求解空间分数阶Klein-Gordon方程的算法.得到的数值格式简单,编程实现容易.运用较低的多项式次数就得到了对解很好的逼近.从算法的推导可以看出,该算法可以推广到二维和三维情形.文中给出的数值算例验证了上述算法的有效性和可行性.
[1] Kusnezov D,Bulgac A,Dang G.Quantum levy processes and fractional kinetics[J].Physical Re-view Letters,1999,82(6):1136-1139.
[2] Mainardi F.Fractional relaxation-oscillation and fractional diffusion-wave phenomena[J].Chaos Solitons Fractals,1996,7(9):20-31.
[3] Ichise M,Nagayanagi Y,Kojima T.An analog simulation of non-integer order transfer functions for analysis of electrode processes[J].J Electroanal Chem Interfacial Electrochem,1971,33:253-265.
[4] Sun H,Abdelwahab A,Onaral B.Linear approximation of transfer function with a pole of fractional power[J].IEEE Transactions on Automatic Control,1984,29(5):441-444.
[5] Cole K.Electric conductance of biological systems[J].Cold Spring Harb Symp Quant Biol,1933,1:107-116.
[6] Mainardi F.Fractional calculus:some basic problems in continuum and statistical mechanics[J].Course and Lectures-international Centre for Mechanical Sciences,1997,378:291-348.
[7] Rossikhin Y,Shitikova M.Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids[J].Applied Mechanics Reviews,1997,50:15-67.
[8] Deng W.Generalized synchronization in fractional order systems[J].Physical Review E,2007,75(5):1-7.
[9] He J H.Approximate analytical solution for seepage flow with fractional derivatives in porous media[J].Computer Methods in Applied Mechanics and Engineering,1998,167(1):57-68.
[10] El-Sayed A M A,Elsaid A,Hammad D.A reliable treatment of homotopy perturbation method for solving the nonlinear Klein-Gordon equation of arbitrary (fractional) orders[J].Journal of Applied Mathematics,2012,2012:1-13.
[11] Sweilam N H,Khader M M,Al-Bar R F.Numerical studies for a multi-order fractional differential equation[J].Physics Letters A,2007,371:26-33.
[12] Jafari H,Daftardar-Gejji V.Solving linear and nonlinear fractional diffusion and wave equations by ADM[J].Appl Math and Comput,2006,180:488-497.
[13] Hashim I,Abdulaziz O,Momani S.Homotopy analysis method for fractional IVPs[J].Commun Nonlinear Sci Numer Simul,2009,14:674-684.
[14] Lin Y M,Xu C J.Finite difference/spectral approximation for the time fractional diffusion equations[J].J Comp Physics,2007,2(3):1533-1552.
[15] Li X J,Xu C J.A space-time spectral method for the time fractional diffusion equation[J].SIAM J Numer Anal,2009,47:2108-2131.
[16] Wazwaz A M.Compacton solitons and periodic solutions for some forms of nonlinear Klein-Gordon equations[J].Chaos,Solitons and Fractals,2006,28(4):1005-1013.
[17] Li S,Vu-Quoc L.Finite difference calculus invariant structure of a class of algorithms for the nonlinear Klein-Gordon equation[J].SIAM Journal on Numerical Analysis,1995,32(6):1839-1875.
[18] Bao W,Dong X.Analysis and comparison of numerical methods for the Klein-Gordon equation in the nonrelativistic limit regime[J].Numerische Mathematik,2012,120(2):189-229.
[19] 陈一鸣,孙慧,刘乐春,等.Legendre 多项式求解变系数的分数阶Fredholm积分微分方程[J].山东大学学报:理学版,2013,48(6):80-86.
[20] Diethelm K.The analysis of fractional differential equations:an application-oriented exposi-tion using differential operators of Caputo type[M].Berlin:Springer,2010.
