一种基于正交拉丁方序列和光正交码的二维光正交码MOLS/OOC*

杨刘洋， 吕 翔

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

光码分多址(OCDMA:optical code division multiple access)具有异步、宽带、安全可靠和即时接入等优点,将成为未来高速局域网和接入网的优选方案之一.光正交码(OOC: optical orthogonal code)是为光码分多址系统设计的一种专用码,其构造方法的研究不断涌现[1-17].一维OOC的研究始于1989年[1],关于一维OOC的存在性问题和构造方法已有很多研究结果[1-4].目前,二维OOC的构造也已成为研究热点[5-17].二维OOC是在一维光地址码的基础之上,通过扩展波长信道而得到的.根据时间扩频序列和波长扩频序列的不同,可以构造多种二维OOC,已知主要的有素数码(PC:prime code)/PC[5]、PC/扩展二次同余码(EQCC:extended quadratic congruence codes)[6]、OOC/PC[7]、PC/OOC[8]、一次重合跳频码(OCFHC:one-coincidence frequency-hopping)/OOC[9]等.这些二维OOC的构造都需要以素数为基础,而本文提出的基于两两正交拉丁方(MOLS:mutually orthogonal latin squares)组构造的二维OOC突破了素数幂的限制.

对于正交拉丁方(OLS:orthogonal latin squares)的研究也已经取得了一定的成果[18].对于不同阶数的拉丁方,MOLS数目也不相同. Bose,Shrikhande和Parker已经证明对于2阶和6阶不存在OLS[19].已知素数幂阶存在MOLS完备组,而其他阶数(除了2和6阶外)至少存在一对OLS[19],但没有统一的构造方法.

在本文中,首先为了解决MOLS的构造问题,提出了一种新的非素数幂中奇数阶MOLS的构造方法；然后,以MOLS序列作为波长跳频序列,以一维OOC作为时间扩频序列,构造了一种新的二维OOC,即MOLS/OOC.根据拉丁方的阶数不同分为2种情况:1)对于素数幂阶数,用MOLS完备组作为二维OOC的波长跳频序列;2)对于非素数幂中的奇数阶,以MOLS较大数目组作为二维OOC的波长跳频序列.最后,对构造的MOLS/OOC的性能进行了仿真.与PC/OOC相比, MOLS/OOC的波长数与文献[13-14]相似,并不局限于素数幂,充分利用了光码分多址系统(MWOCDMA:mult-wave-length optical code division multiple access)中的有效波长数,而且改善了多波长光码分多址系统的误码率.理论分析表明码字容量逼近理论极限,为渐近最优二维OOC.

1 相关定义和引理

定义1设S为一个n元集{0,1,2,…,n-1},A为S上的一个n×n的方阵A(aij),(0≤i,j≤n-1).若使得A的每行、每列中各元素aij当且仅当出现一次,则称A为S上的一个n阶拉丁方.

定义2设S为一个n元集,A与B为S上2个n阶拉丁方,并令C=A×B为S上的n阶并置方阵.若方阵C的n×n个元素数对互不相同,则称拉丁方A与B为一对n阶两两正交拉丁方(MOLS).拉丁方A,B和并置方阵C分别为

A=(aij),

B=(bij),C=(aij,bij),0≤i,j≤n-1.

定义3将n-1个n阶MOLS叫作一个n阶正交拉丁方完备组.

引理1[20]令n为一个正整数,且A1,A2,…,Ak是k个n阶MOLS,则k≤n-1.即n阶MOLS的最大个数是n-1.

引理2[21]令n=pe为一个正整数,p是素数,e是大于等于1的正整数,则存在n-1个n阶MOLS.

引理3[20]令n为一个正整数,r为S中的非零整数,使得(r,n)=1.并令A为n×n的方阵,第i行j列上的元素为

aij=r×i+j(modn).

(1)

式(1)中,0≤i,j≤n-1.则A为基于S上的n阶拉丁方.

2 不同阶数MOLS的构造

已知2阶和6阶的特殊情况,在组合数学中已经被证明不存在MOLS.由引理2和定义3可知,素数幂的阶数存在并且可以构造出MOLS完备组.对非素数幂的阶数是否存在MOLS完备组,虽然是世界上目前未能解决的难题之一,但是可以通过一些方法构造出较大数目的MOLS.本文的构造方法主要基于以下新提出的定理.

定理1令n为一个奇正整数,r和s为S中不同的2个非零整数,使得(r,n)=1,(s,n)=1.若A和B均为n×n的方阵,其i行j列上的元素分别为:

aij=r×i+j(modn);

(2)

bij= s×i+j(modn).

(3)

式(2)～式(3)中,0≤i,j≤n-1.则A和B为基于S上的一对n阶正交拉丁方.

证明 由引理3可知,A和B都是n阶拉丁方.设在并置方阵A×B中某个序对(x,y)出现2次,假设出现在第i行j列上和在第k行h列上.再由式(1)～式(3)可得:

r×i+j=r×k+h=x;

(4)

s×i+j= r×k+h=y.

(5)

再将以上方程改写为:

r×(i-k)=h-j;

(6)

s×(i-k)=h-j.

(7)

从而可以得到

r×(i-k)=s×(i-k).

(8)

设i≠k表示不在同一行,则i-k≠0,再由(r,n)=1和(s,n)=1可知,r和s存在乘法逆元.再用(i-k)-1乘以式(8)两边,从而消去i-k,可以得出矛盾:r=s.因此,必然有i=k.将其代入式(4)中可以得到j=h.由此可以推出在并置方阵A×B中每个序对(x,y)都只会出现一次,同时也说明A和B正交.证毕.

对于素数幂阶的MOLS完备组构造,最常用且最有效的方法是用GF(pe)域[21]构造.然而,对于所有大于2的素数阶,既可以使用GF(pe)域构造也可以使用定理1进行构造MOLS完备组.对于非素数幂中的奇数阶,既可以使用“张量积”法[20]构造,也可以使用定理1进行构造MOLS,而且能够构造的MOLS数量等于欧拉函数φ(n)[22].φ(n)是比n小且与n互素的正整数的总数目.对于非素数幂中除去素数的2倍以外的情况,MOLS的构造既可以使用“张量积”法,也可以使用其他方法.对于素数的2倍情况，MOLS的构造不能使用“张量积”法,需要使用其他方法进行构造,比如“差方”法[23].根据现有文献,将已知能够构造出MOLS的最大数目(60阶以内)列出,如图1所示.

使用定理1与用“张量积”法和“差方”法构造MOLS的具体数目对比,如表1.

由图1和表1可以很清楚地看出,对于非素数幂阶数构造MOLS,定理1的方法很明显优于“张量积”法和“差方”法.

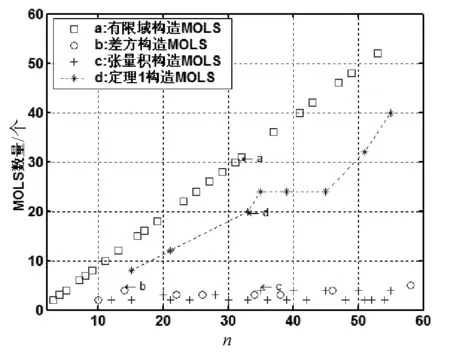
图1 采用4种不同方法构造的MOLS数目对比

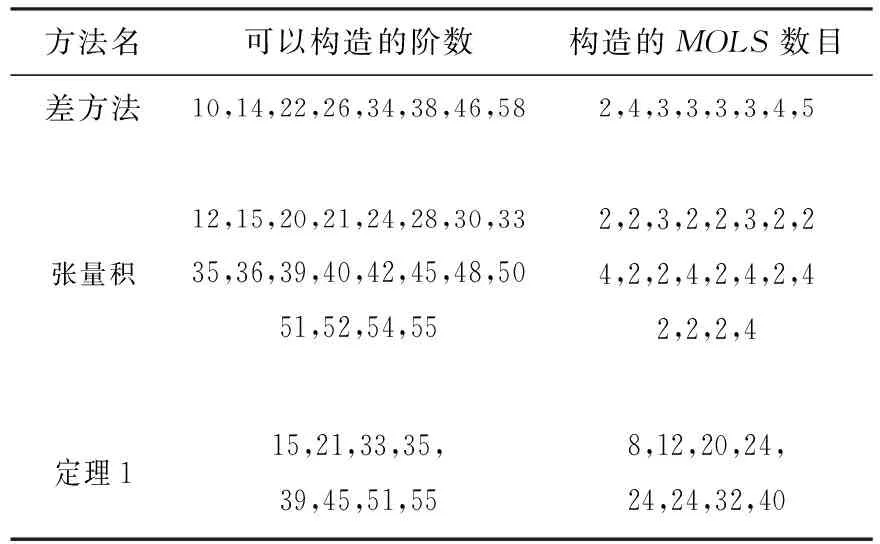
方法名可以构造的阶数构造的MOLS数目差方法10,14,22,26,34,38,46,582,4,3,3,3,3,4,5张量积12,15,20,21,24,28,30,3335,36,39,40,42,45,48,5051,52,54,552,2,3,2,2,3,2,24,2,2,4,2,4,2,42,2,2,4定理115,21,33,35,39,45,51,558,12,20,24,24,24,32,40

3 基于MOLS构造二维光正交码

一维OOC的构造方法参考文献[17],其参数为(L,w,λa,λc),参数中L表示码长,w表示码重,λa表示自相关限,λc表示互相关限.对于满足参数(L,w,1，1)的OOC,其码字容量应满足

(9)

二维OOC可以用m×n矩阵C来表示.其中m表示矩阵的行数(与可用波长数有关),n表示矩阵的列数(称码长,即时间切普数),其参数为(m×n,w,λa,λc).对于二维OOC中的任意2个码字X,Y∈C(X≠Y)在时延τ下应满足的相关限制为:

(10)

(11)

式(10)～式(11)中:xi,j和yi,j分别为X和Y在第i行j列元素;⊕表示模加.

3.1 用MOLS完备组构造二维OOC

对于素数幂,MOLS波长跳频序列的构造方法如下所述.

设拉丁方的阶数为N=pe.

(12)

Hf(0≤f≤N×(N-1)-1).

由以上方法得到MOLS的波长跳频序列组参数用(N,w,λa,λc)表示,N为有效波长数,w=N为码重,λa=0,在同步时λc≤1,依此方法所得MOLS波长跳频序列数的码字容量为N×(N-1).

例如,选择5阶MOLS,即N=5时有5个有效波长(用0,1,2,3,4表示),根据以上方法可以构造出20个MOLS波长跳频序列,如表2所示.

表2 N=5时(5,5,0,3)的MOLS波长跳频序列组

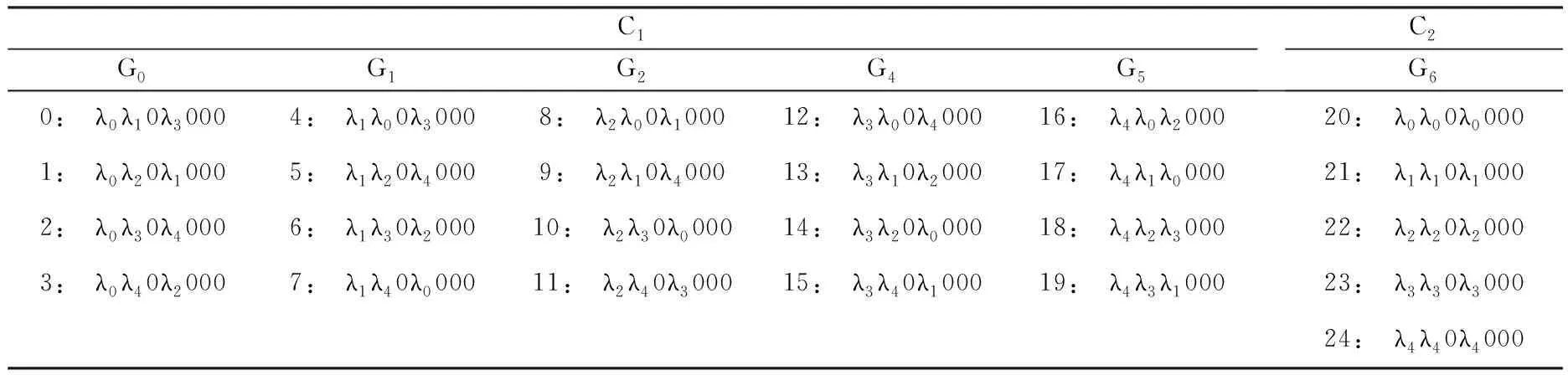
表3 (5,5,0,3)MOLS/(7,3,1,1)OOC的码字集C

图2 码字集C1中码字(λ0λ10λ3000)的自相关函数

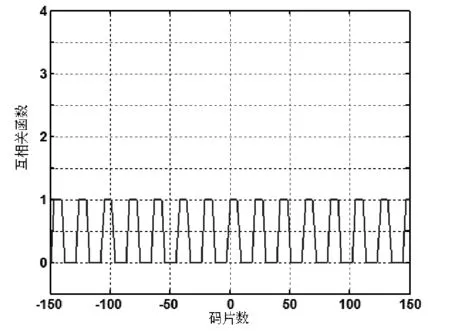
图3 码字集C1中码字(λ0λ10λ3000)和码字(λ1λ0λ3000)的互相关函数

选用(L,w,λa,λc)OOC作为时间扩频序列,并用(N,w,λa,λc)MOLS作为波长跳频序列,即可构成一种新的二维OOC.由于MOLS波长跳频序列的码重为N,因此,OOC的码重w不能超过N.例如当N=5时,OOC为(7,3,1,1)的一个码字为C∶1101000.由于N=5,构造的MOLS波长跳频序列有20个,则总共可以产生20个二维OOC,见表3中的码字集C1.将OOC码字中的所有“1”脉冲代之以相同的波长,可以得到Φooc×N的MOLS/OOC码字,如表3中的码字集C2.对码字集C1中的部分二维码字,根据式(10)～式(11)对其自相关限和互相关限分别进行了仿真,如图2和图3.一般情况下,对于给定的(L,w,1,1)OOC和给定的(N,w,λa,λc)MOLS,构成的MOLS/OOC的码字容量为N×N×Φooc.从此可以看出,根据需要可以单独选择MOLS和OOC.

3.2 用MOLS较大组构造二维OOC

对于非素数幂阶MOLS的构造方法有多种,比如“张量积”法、“差方”法、定理1构造法等.本节将用定理1来构造MOLS波长跳频序列,其构造方法如下所述.

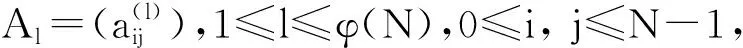
(13)

φ(N)=N×(1-1/p1) (1-1/p2)…

(1-1/pk).

(14)

Hf(0≤f≤φ(N)×N-1).

由以上方法得到的MOLS波长跳频序列组参数用(N,w,λa,λc)表示,其中有效波长数为N,码重为w=N,自相关限为λa=0,在同步时互相关限λc≤1,依此方法所得MOLS波长跳频序列数,即码字容量为φ(N)×N.

例如,选择15阶MOLS,即N=15时有15个有效波长(用1,…,15表示).由于φ(15)=8,所以根据以上方法可以构造出120个长度为N的波长跳频序列.限于篇幅,在此只给出前8个序列,如表4.选用 (L,w,λa,λc)OOC作为时间扩频序列,并用N阶MOLS构造的(N,w,λa,λc)MOLS序列作为波长跳频序列,构造二维OOC.由于MOLS波长跳频序列的码重为N,因此,OOC的码重w不能超过N.例如当N=15时,OOC为(7,3,1,1)的一个码字为C∶1101000.由于N=15,构造的MOLS波长跳频序列有120个,故总共可以产生120个二维OOC码字.限于篇幅,在此只给出前16个和后8个码字,见表5中的码字集C1.将OOC码字中的所有“1”脉冲代之以相同的波长,可以得到ΦOOC×N的二维MOLS/OOC码字,如表5中的码字集C2.对码字集C1中的部分二维码字,根据式(10)～式(11)对其自相关限和互相关限分别进行了仿真,结果见图4～图5.一般情况下,对于给定的(L,w,1,1)OOC和(N,w,λa,λc)MOLS,且w≤N,构造的MOLS/OOC码字容量为

N×(1+φ(N))×ΦOOC.

定理2基于GF(pe)域和定理1构造的MOLS中,任意2个列序列在同步时的重复个数不大于1.

证明 从基于GF(pe)域和定理1构造的所有MOLS中任取两个列序列H1和H2.

1)当H1和H2取自同一个拉丁方时

根据定义1可知,拉丁方的每行、每列中各元素aij当且仅当出现一次,说明一个拉丁方中行与行之间、列与列之间各个元素都不重复.同时说明,在同步时一个拉丁方的所有列序列中任意2个序列的重复个数为0.

表4 N=15时(15,15,0,15)的MOLS波长跳频序列组

表5 (15,15,0,15)MOLS/(7,3,1,1)OOC的码字集C

图4 码字集C1中码字(λ0λ20λ4000)的自相关函数

图5 码字集C1中码字(λ0λ20λ4000)和码字(λ0λ40 λ8000)的互相关函数

2)当H1和H2取自不同的拉丁方时

假设H1和H2中分别有2个元素出现重复,分别为x,y.由于H1和H2取自不同的拉丁方,所以根据式(12)可得:

(15)

(16)

①若ai=0,则

(17)

(18)

由于x和y分别在同一列不同行,所以x和y不会出现2次,x和y中只有一个出现重复.

②若ai≠0,则

(19)

因此,H1和H2中元素的重复个数不大于1.同时说明,在同步时H1和H2序列的重复个数不大于1.

综上所述,在同步时H1和H2的重复个数不大于1.以上定理2得证.证毕.

4 二维MOLS/OOC码的性能分析

由于MOLS波长跳频序列的自相关限为0,所以C1中每个码字的自相关限也是0.尽管C2的每个码字中1脉冲的波长相同,但由于采用的是(L,w,1,1)OOC,自相关旁瓣最大值为1，因此,构造MOLS/OOC码字的自相关限也为1.对于互相关限，应考虑以下几种情况:

1)相同的时间扩频序列/不同波长跳频序列.由于OOC的自相关限为1,并且由定理2可知,MOLS波长跳频序列的互相关在同步时不大于1,所以MOLS/OOC码字的互相关限为1.

2)不同的时间扩频序列/相同的波长跳频序列.由于OOC的互相关限为1,因此,MOLS/OOC码字的互相关限为1.

3)不同的时间扩频序列/不同的波长跳频序列.同样由于OOC的互相关限为1,因此,MOLS/OOC码字的互相关限为1.因此,①当N为素数幂时,二维MOLS/OOC码字的参数为(N×L,w,1,1),码字容量为N×N×ΦOOC;②当N为非素数幂时,MOLS/OOC码的参数为(N×L,w,1,1),并且码字容量为N×(1+φ(N))× ΦOOC.

下面具体分析MOLS/OOC码字的互相关均值,先让任意一个码字A的时间平移L次,统计该码字与其余N×(1+φ(N))×ΦOOC-1个码字在时间和波长上都重合的“1”的个数(碰撞数),然后计算互相关均值.分以下几种情况进行介绍.

1)与A具有相同的时间扩频序列,但波长跳频序列不同.总共有N×(1+φ(N))-1个不同的波长跳频序列,对应的不同码字数为N×(1+φ(N))-1个.分以下2种情况：①阶数为素数幂时,共有N×N-1个码字,有N×w2-w次碰撞；②阶数为非素数幂时,共有N×(1+φ(N))-1个码字,有φ(N)+3w-3次碰撞.

2)与A具有不同的时间扩频序列,但有相同的波长跳频序列.总共有φOOC-1个不同的码字,所以共有(ΦOOC-1)w个碰撞.

3)与码字A具有不同的时间扩频序列,而且波长跳频序列也不同.总共有Φ(OOC-1)(N×(1+φ(N))-1)不同的码字,与1)的分析类似，分为2种情况:①阶数为素数幂时,共有(ΦOOC-1)(N×w2-w)个碰撞；②阶数为非素数幂时,共有(ΦOOC-1)(φ(N)+3w-3)个碰撞.

因此,任意一个码字A水平移L次,与其余N×(1+φ(N))×ΦOOC-1个码字发生碰撞的总次数为:

1)阶数为素数幂时,

Y1=N×w2-w+ (ΦOOC-1)w+

(ΦOOC-1) (N×w2-w)=

N×ΦOOC×w2-w.

(20)

2)阶数为非素数幂时,

Y2=φ(N)+3w-3+(ΦOOC-1)w+

(ΦOOC-1) (φ(N)+3w-3)=

ΦOOC(4w+φ(N)-3)-w.

(21)

考虑到用户等概率地发送数据比特“0”和“1”, 则MOLS/OOC码字的互相关均值为:

(22)

(23)

假设多波长光码分多址系统中有K个并发用户数,则采用MOLS/OOC码字的多波长码分多址系统的误比特率[17]为

(24)

在此处笔者只考虑用户多址干扰的影响,忽略光电探测过程中的热噪声和散弹噪声,判决门限取MOLS/OOC的码重Th=w.下面针对多波长光码分多址系统中不同码字参数的MOLS/OOC码字分2种情况进行讨论.

1)给定(N,w,λa,λc)MOLS跳波长序列,给定(L,w,1,1)OOC扩时序列的码重w,增加OOC的码长L.根据式(17)～式(18),MOLS/OOC的码字互相关均值u1和u2都降低.因此,在相同并发用户数的情况下,多波长光码分多址系统的误码率(BER)也降低.例如,波长跳频序列MOLS为(5,5,0,3),扩时序列OOC分别为(7,3,1,1)和(11,3,1,1),这两种情况下的MOLS/OOC的码字容量都为25.多波长光码分多址系统的误码率与并发用户数的关系如图6所示.OOC的码长越长,多波长光码分多址系统的误码率就越低.

2)给定(L,w,1,1)OOC扩时序列,由于(N,w, λa,λc)MOLS跳波长序列的码长和波长数相同,都为N,所以当增加波长数N时,MOLS/OOC的码字容量增加.根据式(17)～式(18)，MOLS/OOC的码字互相关均值u1和u2都降低.因此,多波长光码分多址系统的误码率也降低.例如,扩时序列OOC参数为(7,3,1,1),波长跳频序列MOLS分别为(15,15,0,15)和(21,21,0,21),在这两种情况下MOLS/OOC的码字容量分别为135和273. 多波长光码分多址系统的误码率与并发用户数的关系如图7所示.

图7 不同波长数时多波长光码分多址系统误码率与并发用户数的关系

图6 不同码长时多波长光码分多址系统误码率与并发用户数的关系

MOLS跳波长序列的波长数越多,多波长光码分多址系统的误码率就越低.

由文献[17]可知,等重对称二维OCDMA码的理论上界为

Φ(m×n,w,λ,λ)≤

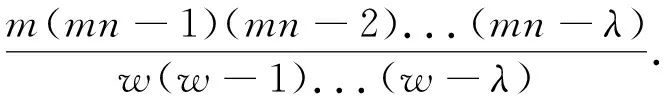
(25)

由此可得

(m×n,w,λ,λ)=(N×nOOC,w,1,1)

码的理论上界为

ΦMOLS/OOC≤Φ(N×nOOC,w,1,1)≤

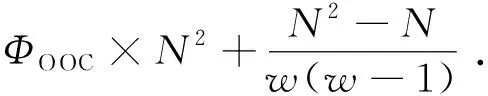
(26)

其中,nOOC=w(w-1)ΦOOC+1.

当w较大时,二维MOLS/OOC码的实际码字容量N×(φ(N)+1)×ΦOOC,与式(26)的理论上界很接近,所以文中构造的MOLS/OOC码为渐近最优二维OOC.

5 结 论

通过以上的构造实例和仿真性能分析可以得到如下结论.

首先本文提出的非素数幂中奇数阶MOLS组的构造方法与其他方法相比具有构造的MOLS数目更大的优点.然后,本文提出的基于MOLS和OOC构造的MOLS/OOC与文献[7-8]中的PC/OOC对比,前者的波长数与文献[13-14]等中的波长数相似,并不局限于素数幂.最后,仿真结果表明当MOLS/OOC码字的其他参数相同时,码长越长误码率越低,或者有效波长数越多误码率越低.理论分析表明,MOLS/OOC的码字容量逼近理论极限,为渐近最优二维OOC.

在将来进一步的工作中,如果对于非素数幂的阶数能够构造出MOLS完备组,将具有更多数目的MOLS,则用本文提出的二维OOC的构造方法可以构造的码字容量将更大.当然也可以与其他的扩时序列结合,构造更多新的二维OOC.

参考文献：

[1]Auslander M,Reiten I,Smalo O S.Representation theory of Artin algebras[M].Cambridge:Cambridge University Press,1995.

[2]Miyashita Y.Tilting modules associated with a series of idempotent ideals[J].Journal of Algebra,2001,238(2):485-501.

[3]Auslander M.Relative homology and representation theory I:Relative homology and homologically finite subcategories[J〗.Communications in Algebra,1993,21(9):2995- 3031.

[4]朱勇,张宝富,李玉权.光正交码的有限射影几何设计构造方法[J].通信学报,1999,20(1):28-33.

[5]Tancevski L,Andonvic I.Wavelength hopping/time spreading code division multiple accees systems[J].IEEE Electronics Letters,1994,30(17):1388-1390.

[6]Tancevski L,Andonvic I.Hybrid wavelength hopping/time spreading schemes for use in massive optical networks with increased security[J]. IEEE/OSA Journal of Lightwave Technology,1996,4(12):2636-3647.

[7]Sheng Pengwan,Yu Hu.Two-dimensional optical system with prime/OOC codes[J].IEEE Photonics Technology Letters,2001,13(13):1373-1375.

[8]Kwong W C,Yang Guchang,Varghese B,et al.Multiple-wave-length optical orthogonal codes under prime sequence permutations for optical CDMA[J].IEEE Trans On Communications,2005,53(1):117-123.

[9]Sun Shurong,Yin Hongxi,Wang Ziyu,et al.A new family of 2-D optical orthogonal codes and analysis of its performance in optical CDMA access networks[J].IEEE/OSA Journal of Ligthwave Technology,2006,24(4):1646-1653.

[10]Happel D.Triangulated categories in the representation theory of finite dimensional algebras[M].Cambridge:Cambridge University Press,1988.

[11]Hu Wei,Xi Changchang.D-split sequences and derived equivalences[J].Adv Math,2011,227(1):29-318.

[12]Ji Jianhua,Fan Ge.A new family of two-dimensional optical orthogonal codes for massive optical CDMA networks[J].Acta Photonica Sinica,2002,31(6):676-680.

[13]吉建华,徐铭,张志朋,等.一种基于扩展素数码和单重合序列的二维光正交码EPC/OCS[J].光子学报,2007,36(7):1285-1288.

[14]吉建华,田晶晶,莫浩然,等.一种新的二维光正交码及其性能分析[J].中国激光,2007,34(5):667-670.

[15]吉建华,范戈.基于扩展的双曲同余码/素数码的二维光正交码[J].上海交通大学学报:自然科学版,2002,36(12):1765-1769.

[16]黄月梅,周君灵.一类权重为4 的二维光正交码[J].北京交通大学学报：自然科学版,2012,36(6):144-146.

[17]殷洪玺.光码多分址编码理论与应用[M].北京:清华大学出版社,2013:98-118.

[18]Dens J,Keedwell A D.Latin squares new developments in the theory and applications[M].North-Holland:Annals of Discrete Mathematics 46,1991.

[19]Bose R C,Shrikhande S S,Paker E T.Further results on the construction of mutually orthogonal Latin squares and the falsity of Euler′s conjecture[J].Canadian J Math,1960,12:189-203.

[20]张秀平.组合数学[M].北京:北京师范大学出版社,2011:173-179.

[21]魏万迪.组合论(下册)[M].北京:科学出版社,2010:309-311.

[22]卢开澄,卢华明.组合数学[M].北京:清华大学出版社,2004:248-249.

[23]Van J H,Wilson R M.A course in combinatorics[M].2nd ed.Beijing:China Machine Press, 2004:294-300.