考虑边界土体性质悬浮隧道地震响应分析
2014-08-06晁春峰
晁春峰
(浙江省交通科学研究院,杭州 310006)
0 引 言
进入21世纪以来,国家社会、经济等领域迎来了全面高速发展的黄金时期,大江、大河和湖泊上都修建了各种类型的桥梁、隧道等交通结构物,把各个城市紧紧的联系起来,方便了人们的生活。然而,我国大陆与台湾岛、海南岛之间的交通,仍然依赖于昂贵的空中交通或者低速的海轮。随着商业贸易、文化交流日益繁忙,建设固定交通通道势在必行。但世界上最长的桥梁杭州湾跨海大桥和胶州湾跨海大桥,全长仅有36km,只是台湾海峡宽度的五分之一,由此可见,采用传统桥梁来建设跨越海峡,其技术难度和经济成本难以想象。
悬浮隧道 (Submerged Floating Tunnel,简称“SFT”)是一种新型的跨越长、深水域的交通结构物,相比传统桥梁或隧道具有强大的竞争优势和发展潜力:①当跨越较大跨度及深水的水域时 (一般跨度超过1000m,水深超过50m),悬浮隧道的单位长度造价不会显著增加;②悬浮隧道在自然环境作用下 (大风、雨、雪、雾等),可以不受影响的正常使用,有效利用率高。但悬浮隧道所处环境完全不同于传统的桥梁或隧道,其受波、流或地震等作用的影响较为复杂[1],尽管各国学者对此进行了大量的研究和探索,但目前其技术还不够成熟,尤其是设计和施工方法,还未上升到规范的层面,因此至今为止世界上还未建成一座悬浮隧道。
我国东部沿海是悬浮隧道未来建造的地区之一,但该区域位于环太平洋地震带上,因此需要重点研究悬浮隧道在地震作用下的动力特性。关于悬浮隧道的地震影响分析,已有不少学者做了若干探索研究,提出了一些分析方法。Brancaleoni等[2](1989)提出了在地震和波浪作用下悬浮隧道动力响应计算方程,并对锚索固定的短跨径和水下墩支撑的长跨径两种类型的悬浮隧道进行了地震响应分析;Fogazzi等[3](2000)和 Di Pilato等[4](2008)利用三维空间梁单元,开发了能模拟水-结构耦合和土-结构耦合的计算程序,并构造了大变形锚索单元,在此基础上研究了悬浮隧道多点支撑地震效应;Chen等[5](2010)采用大质量法,考虑了地震行波效应,研究了悬浮隧道的地震响应。上述相关的研究,基本上将边界简单地模拟成简支、固支或弹性支撑,还不能反映两端土体-驳岸结构相互作用对结构地震响应的影响,没有对悬浮隧道驳岸结构引起的边界条件变化进行更加深入的探讨。
本文考虑横向地震作用下悬浮隧道驳岸结构周围岩土性质对边界条件的影响,建立三维土弹簧约束的悬浮隧道数值模型,采用大质量法,结合我国东部海域海床岩土性质,并参照意大利Messina海峡悬浮隧道设计方案的参数[6],详细分析了边界岩土性质、驳岸结构设计等对悬浮隧道地震响应的影响。
1 计算模型
1.1 力学模型的简化及模拟
由水下锚索锚固的悬浮隧道结构 (例如Messina海峡悬浮隧道方案[6])如图1所示,管体两端为驳岸结构,埋设于海床岩土中;中间为悬浮于水中的封闭管体;管体由水下锚索锚固于海底基础上。在海洋环境中,水流力、波浪力的长期循环作用,会使驳岸结构边界土体性质发生变化 (暂不考虑水下锚索基础边界土体性质的变化)。因此,两端土体对悬浮隧道管体的约束作用采用3个方向上的线性土弹簧单元近似模拟,并通过改变土弹簧刚度来近似模拟土体性质的变化。结构周围水体对结构的作用,采用Morison方程近似模拟,暂不考虑地震波在水体中的传播对结构产生的动水压力。
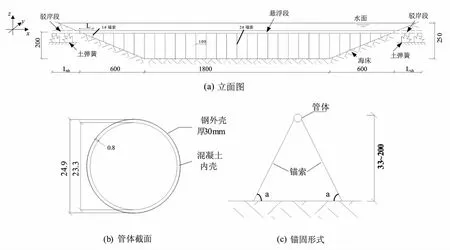
图1 悬浮隧道示意图 (单位:m)
1.2 土弹簧动刚度确定
土弹簧竖向 (z向)动态刚度[7]定义为:KV=ΔFV/ΔδV,其中ΔFV为单位长度驳岸段与土体之间的动态竖向力,ΔδV为驳岸段的竖向位移;土弹簧横向 (y向)和纵向 (x向)动态刚度[7]定义为:KL=ΔFL/ΔδL,其中ΔFL为单位长度驳岸段与土体之间的动态横向或水平向力,ΔδL为驳岸段的衡向或水平向位移。
当驳岸段长度Lsh大于10倍的管体与土体的接触宽度B时,可以将悬浮隧道驳岸段管体等效为弹性地基上的半无限长梁,则土弹簧竖向、横向和纵向动态刚度可以分别表示为:

1.3 水作用力模型
单位长度柱体在静水中运动时受到的水作用力,可用Morison方程给出:
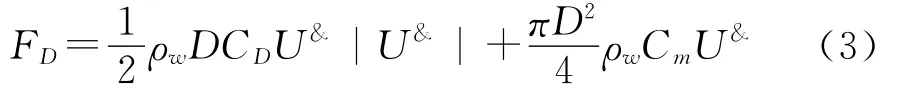
式中:CD为锚索的阻力系数,Cm为附加质量系数,U为柱体相对水体的位移;ρW为水密度,D为柱体特征长度。对雷诺数Re>2.5×105的柱体,可取CD=0.7、Cm=1.0。
2 典型案例的模型参数
由于目前世界范围内还没有建成悬浮隧道,因此,本文选用文献[6]研究过的Messina海峡悬浮隧道设计及有关参数作为案例进行分析计算,该悬浮隧道的基本参数见表1。并在此设计方案的基础上,运用所提出的理论方法,对其多个设计参数进行参数分析,详细研究悬浮隧道考虑边界土体不同性质时,其对地震响应特性的影响。
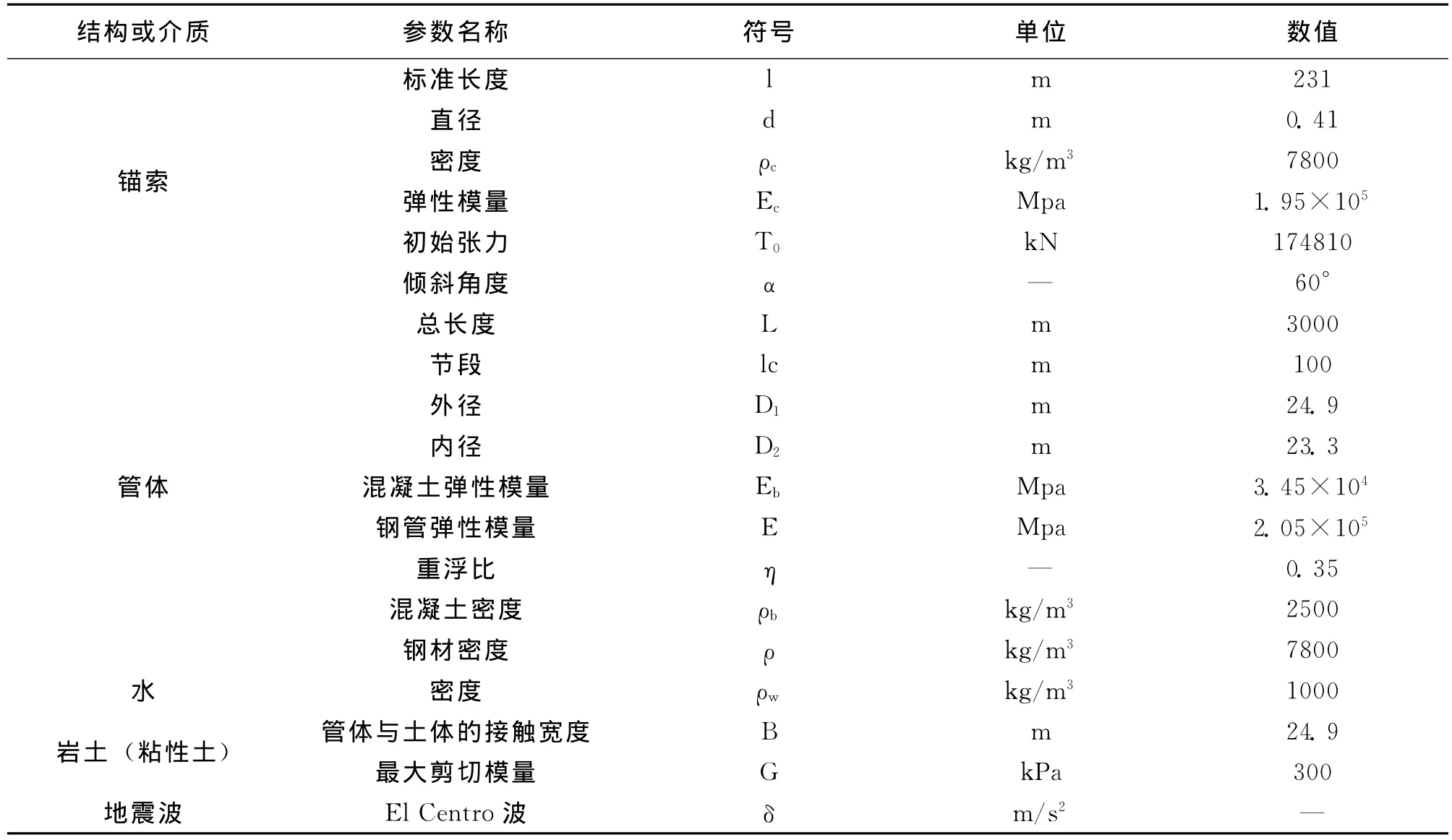
表1 典型计算实例的基本参数
3 地震响应的分析比较
为探求考虑悬浮隧道边界土体性质对其地震响应特性的影响,本文对驳岸段长度Lsh、粘性土剪切模量G等参数进行了悬浮隧道地震响应的参数研究。
3.1 边界土体性质对地震响应的影响
对悬浮隧道动力特性的研究中,一般对驳岸段结构的约束都简单的等效为铰支或固支,并认为实际受力情况介于上述两种约束情形之间。图2给出了在不同驳岸段结构的约束方式下,地震对悬浮隧道管体及锚索受力的影响。从图2可知,悬浮隧道管体在地震作用下的位移最大值均出现于跨中,在弹性支撑下 (土弹簧)的位移最大值明显地小于约束为铰支和固支情况下的值,减小幅度分别达14%和16%;不同约束下管体最大弯矩也均出现于跨中,弹性支撑的弯矩值大于铰支值,小于固支值;锚索索力增量 (张力和弛力)最大值出现于两端 (短索),弹性支撑值达到铰支值或固支值的约1.5倍,而跨中锚索索力增量则略小于铰支值和固支值;管体最大扭矩值也出现于两端 (扭矩约束点),弹性支撑值略小于铰支值,与固支值相当,在跨中其值大幅小于铰支值和固支值。因此,可以看出,简单把驳岸结构约束简化为铰支和固支并不完全合理,特别是对于索力,会导致锚索设计的不安全。
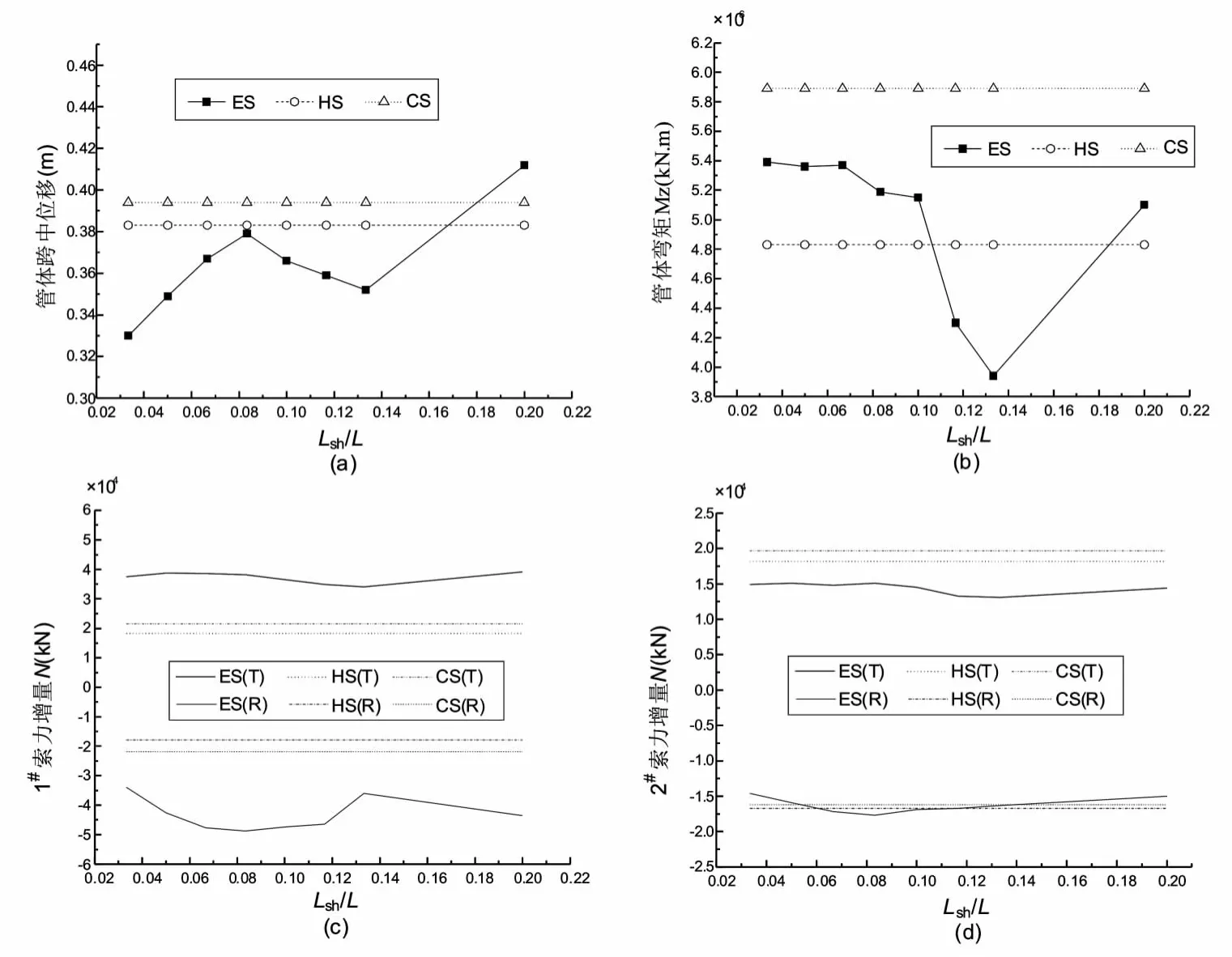
图3 驳岸段长度对地震响应的影响
3.2 驳岸段长度对地震响应的影响
图3 给出了驳岸段长度对管体跨中位移 (图3a)、管体跨中弯矩 (图3b)、1#索 (图3c)和2#索 (图3d)的影响。从图中可以看出,驳岸段计算长度的变化对管体跨中位移和弯矩及锚索索力均具有较大影响。在驳岸段计算长度Lsh=100m~400m (Lsh/L=0.033~0.13)范围内,驳岸段长度的增加对管体跨中位移、跨中弯矩和锚索索力均具有明显的影响,但其影响并不是线性的,而是波动的。其中跨中位移最大变化幅度为15%、跨中弯矩最大变化幅度为27%、1#索索力增量最大变化幅度为12% (张力)和30% (弛力)及2#索索力增量最大变化幅度为13% (张力)和17% (弛力);但是随着驳岸段计算长度的继续增加Lsh>400m,管体跨中位移会大幅的增大,跨中管体弯矩和锚索索力也明显增大。因此,悬浮隧道驳岸段的设计需要考虑多方面的因素,其计算长度选取必须按实际情况确定,假定为简单约束可能会产生较大误差。
3.3 粘土剪切模量对地震响应的影响
图4给出了粘土剪切模量对管体跨中位移 (图4a)、管体跨中弯矩 (图4b)、1#索 (图4c)和2#索 (图4d)的影响。从图中可以发现,随着粘土剪切模量G的增大,总体趋势上管体跨中位移和弯矩均会显著地增大,而1#索索力增量则会大幅度减小,因为刚度越大的弹性约束更加接近于固支约束条件,2#索索力增量也会出现明显的波动。但从局部变化看,粘土剪切模量的变化对悬浮隧道地震响应影响规律并不是线性的,而是波动的。其中管体跨中位移在Su/Ip≤8范围内增幅为25%、在Su/Ip>8时最大变化幅度为5%以内;管体跨中弯矩在Su/Ip≤8范围内增幅为29%、在Su/Ip>8时最大变化幅度为16%以内。锚索索力增量变化较为复杂,1#索索力增量在Su/Ip≤6范围内张力增幅为19%,随后大幅减小35%并趋于稳定,而弛力则相对平缓的减小35%后接近固支约束值;2#索索力增量变化又不同于1#索,其张力最大变化幅度为15%,弛力最大变化幅度为50%。当Su/Ip>10时,结构刚度矩阵接近病态,计算结果无法采信。但是根据常理可知,当粘土变硬,则边界条件越接近固支,因此,图中虚线部分是其趋势。综合上述现象,可知土体性质的变化会对悬浮隧道地震响应特性带来巨大影响,但是其影响规律较为复杂,可能与悬浮隧道结构动力特性、地震波的特性等因素相互影响,需要进一步对各种实际情况的计算才能给出合适的计算结果,这对将来设计建造悬浮隧道带来一定程度上的困难。
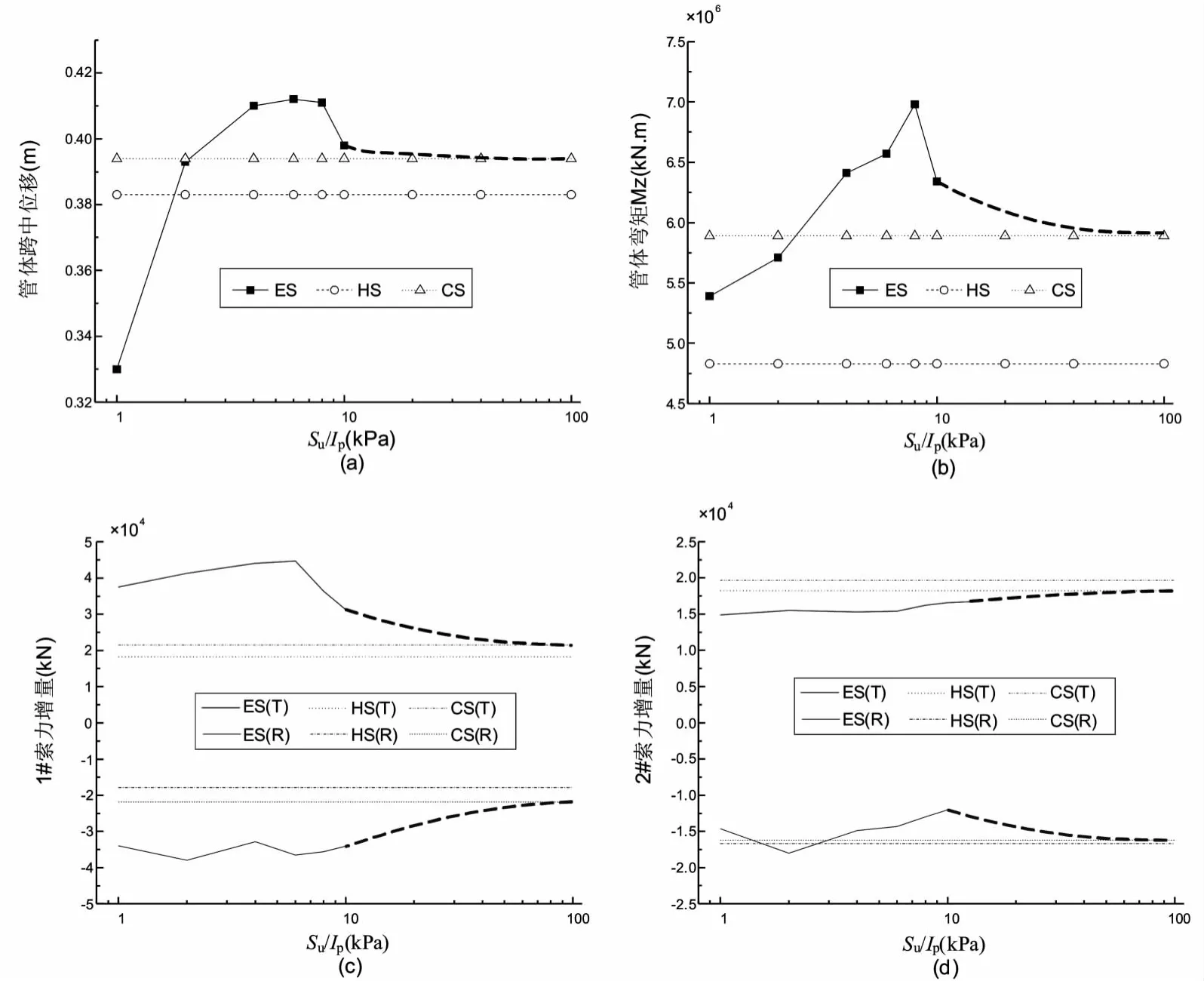
图4 粘土剪切模量对地震响应的影响
4 结 语
本文在考虑土体性质对驳岸段结构约束影响的基础上,研究了横向地震作用下悬浮隧道的地震响应,并以Messina海峡悬浮隧道方案为基本模型,计算得到了其在地震作用下悬浮隧道管体位移、弯矩、扭矩和锚索索力,并对驳岸段长度Lsh和粘性土剪切模量G进行了参数分析,得到以下结论:
(1)横向地震作用下,悬浮隧道管体的最大位移、弯矩和扭矩均出现于管体跨中,锚索索力增量最大值出现于短索;弹性支持下,管体最大位移和扭矩会减小,最大弯矩则介于铰支值和固支值之间,短索索力值则会大幅增大;
(2)驳岸段计算长度的变化对管体跨中位移和弯矩及锚索索力均具有较大影响,但其对管体位移、弯矩和锚索索力的影响是波动的;在一定长度范围内,驳岸段结构对悬浮隧道地震响应是有利的,超过该范围后,驳岸段结构将对悬浮隧道地震响应产生不利影响;
(3)粘土剪切模量的变化会对悬浮隧道地震响应特性带来显著影响,其影响规律也是波动的,可能与悬浮隧道结构动力特性、地震波的特性等相关参数具有耦合关系,需要进一步的研究探索。
(4)在悬浮隧道地震响应分析中,不能把驳岸结构处理成简单的约束形式 (铰支、固支或一般弹性支撑),应考虑其实际约束情况,不然会产生较大的计算误差。
[1]项贻强,晁春峰.悬浮隧道管体及锚索耦合作用的涡激动力响应[J].浙江大学学报:工学版,2012,46(3):409-415.
[2]Branchaleoni F,Castellani A,D'Asdia P.The response of submerged tunnels to their environment[J].Engineering Structures,1989,(11):47-56.
[3]Fogazzi P,Perotti F.The dynamic response of seabed anchored floating tunnels under seismic excitation[J].Earthquake Engineering and Structural Dynamics,2000,(29):273-295.
[4]M.Di Pilato,F.Perotti,P.Fogazzi.3Ddynamic response of submerged floating tunnels under seismic and hydrodynamic excitation[J].Engineering Structures,2008,30 (1):268-281.
[5]Chen Wenjun,Huang Guojun.Seismic wave passage effect on dynamic response of submerged floating tunnels[C]//Proceedings of first international symposium on Archimedes Bridge,Chun′an:Procedia Engineering,2010, (4):217-224.
[6]G.Martire,B.Faggiano,F.M.Mazzolani,et al.Seismic analysis of a SFT solution for the Messina Strait crossing[C]//Proceedings of first international symposium on Archimedes Bridge,Chun’an:Procedia Engineering,2010,(4):303-310.
[7]Det Norske Veritas.DNV Recommend Practice,Free Spanning Pipeline[S].Norway:Det Norske Veritas,2006.
[8]郑志昌,陈俊仁,朱照宇.南海海底土体物理力学特征及其地质环境初步研究[J].水文地质工程地质,2004,31(4):50-54.
