一类半线性椭圆型方程组非平凡解的存在性

彭超权,王 芳,刘 颖

(中南民族大学 数学与统计学学院,武汉430074)

1 主要问题及结果

本文考虑如下一类半线性椭圆型方程组:

(1)

过去几十年来,很多学者对非线性椭圆型方程组非平凡解的存在性及其相关性质进行了大量的研究,如下列形式有界域上Dirichlet边界的椭圆型方程组:

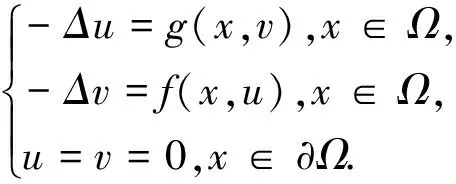
(2)

其中Ω是RN中的光滑有界区域.文[1]和[2]等首先对问题(2)进行了研究,他们在分数维的Sobolev空间中,利用环绕定理得到了问题(2)的非平凡解. 文[3]对渐近线性椭圆型方程组作了研究, 文[4]则考虑了一类非线性项不满足AR条件的方程组非平凡解的存在性.

受上述文章的启发,本文拟考虑问题(1)中非线性项不满足AR条件时非平凡解的存在性.我们假设f,g满足如下条件:

(H1)f,g∈C(R),且有f(t)=g(t)=0,∀t≤0,f(t)>0,g(t)>0,∀t≥0.

|f(t)|,|g(t)|≤C(1+|t|p-1),∀t∈R,

本文的主要结果如下.

2 预备知识

(3)

因此我们可以在E上定义一个新的内积：

由它所诱导的范数是:

‖z‖=(z,z)u|2+2uv+

μ|∀z=(u,v)∈E.

由式(3)可知,‖·‖和‖·‖E等价.因此,当λμ>1时,与方程组(1)所对应的能量泛函可以写为:

(4)

设E为一实的希尔伯特空间，泛函I∈C1(E,R).我们说泛函I在指标c∈R处满足Cerami条件是指:如果当n→∞时,有I(zn)→c并且(1+‖zn‖)I′(zn)→0,那么{zn}存在一个收敛的子序列.

为了证明定理1，我们将用到文[5]中提出的山路定理.

3 定理1的证明

引理2 假设条件(H1)～(H3)成立，则有:

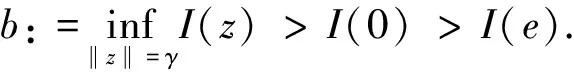
证明对∀z=(u,v)∈E,ε>0,由条件(H1)～(H3)以及Sobolev嵌入定理可知:

这说明当ε充分小时,存在ρ>0使得:

固定z=(u,v)∈E,令e=(tu,tv)，由条件(H3)可知,当t充分大,I(tu,tv)<0，从而结论成立.

引理3 对于由式(4)定义的泛函I,若条件(H1)～(H4)成立,并且对任意{zn}⊂E都有当n→∞时I′(zn),zn→0，那么存在{zn}的一个子列,我们仍然用{zn}表示,使得对所有t∈R,n∈N有

(5)

对∀t>0,式(5)说明:

这说明对所有t>0，都有h(t)≤h(1)，因此,

(6)

另一方面,由式(5)可知：

因此,根据式(6)可得：

引理4 由式(4)定义的泛函I满足(c)c条件.

证明假设{zn}⊂E满足I(zn)→c,(1+‖zn‖)‖I′(zn)‖E*→0，令:

则‖wn‖在E中有界,因此,由Sobolev嵌入定理可知∃w=(u,v)∈E,使得wn→wa.e.在Ω中,wn→w在Ls(Ω)中,其中s∈[2,2*).

若‖zn‖→∞，我们断言

w(x)≢0.

(7)

事实上,若w(x)≡0在Ω中,则:

(8)

矛盾,因此,{zn}在E中有界.

定理1的证明定理1可直接由引理1、引理2及引理4得到.

参 考 文 献

[1] Hulshof J, Van De V R.Differential systems with strongly indefinite varational structure[J].J Funct Anal,1993,114:32-58.

[2] De Figueiredo D G, Felmer P L.On superquadratic elliptic systems[J]. Tras Amer Math Soc,1994,343:99-116.

[3] Li G B,Yang J F.Asymptotically linear elliptic systems[J].Comm Partial Differential Equations,2004,29(5/6):925-954.

[4] Li G B,Wang C H.The existence of nontrivial solutions to a semilinear elliptic system onRNwithout the Ambrosetti-Rabinowibz condition[J]. Acta Math Sci,2010,30B(6):1917-1936.

[5] Zhou H S. An application of a Mountain Pass theorem[J].Acta Math Sci,2002,18(1):27-36.