三维拓扑绝缘体的磁电耦合效应与冷暗物质轴子

李成德

(中南民族大学 电子信息工程学院，武汉 430074)

量子物理领域一系列新奇的量子现象和量子物态的发现，推动了以纳米材料为代表的众多高新科技的应用与发展.随着电子学和半导体工业的飞速发展，各种电子信息技术产品已经应用到生活的各方面.半导体芯片上单位面积晶体管的数目的快速增加，使得晶体管的微观尺寸逼近纳米范围，量子尺寸效应越来越明显，器件热耗散等问题日益突出，传统的半导体工业已经濒临发展的极限.在应用需求的驱动下，自旋电子学[1-3]应运而生. 基于自旋特性的电子器件利用电子的自旋自由度而非电子的电荷来存储和处理信息，与传统的电子器件相比，可以有更低的能量损耗和更快的信息处理速度，而且可以与量子信息技术很自然地对接.

拓扑绝缘体(TI)[4-6]是随着自旋电子学的发展而新出现的一种全新的量子物态.拓扑绝缘体的由来与量子霍尔效应(QHE)、量子自旋霍尔效应(QSHE)等现象紧密相连[8-12].拓扑绝缘体的体态和普通的绝缘体一样，费米能级附近存在能隙.但是在自旋轨道耦合作用下，拓扑绝缘体的表面(对应三维拓扑绝缘体)或与普通绝缘体的界面上会出现无能隙、且具有线性色散关系的表面态或边界态(对应二维拓扑绝缘体)，这些电子由无质量的狄拉克(Dirac)方程来描述，其边界态受时间反演对称性保护，不存在由于杂质导致的背散射，由此电阻和能耗很小，可望克服现有微电子产业所面临的功耗和发热问题.理论上，拓扑绝缘体与磁性材料或超导材料的界面处，还可能发现新的物质相和Majorana费米子[7]，它们在自旋电子学和量子计算中会有重要应用.拓扑绝缘体是凝聚态物理的研究热点.本文将介绍拓扑绝缘体与量子霍尔效应、量子自旋霍尔效应等霍尔效应“家族”的关系演化和由来，并且从轴子(Axion)模型的起源角度，探讨了三维拓扑绝缘体的磁电耦合效应以及与冷暗物质(CDM)粒子—轴子的联系和区别，并且介绍可能的实验探测方法.

1 量子霍尔态与拓扑绝缘体

霍尔效应(Hall Effect) “家族”包括传统的霍尔效应、反常霍尔效应(Anomalous Hall Effect)、自旋霍尔效应(Spin Hall Effect)和相应的量子化版本：量子霍尔效应、量子反常霍尔效应(QAHE)、量子自旋霍尔效应(QSHE)[8-12].1879年，美国物理学家艾德文·霍尔(E.H. Hall)发现在通有电流的二维导体中，如果施加垂直于电流方向的磁场，会在垂直于电流和磁场方向的导体两端产生霍尔电压[8].第二年，霍尔在研究磁性金属的霍尔效应时，发现即使不加外磁场也可以观测到霍尔效应，这就是反常霍尔效应.霍尔效应被发现18年后电子的概念才首次被提出，所以霍尔效应的物理机制在当时并不清楚.现在我们知道，霍尔效应是由于磁场中的电子在运动过程中受到洛伦兹力而产生偏移的.理论与实验研究表明，霍尔电压与外加磁场强度是线性关系，该直线的斜率(称为霍尔系数)的大小和符号由导体中载流子浓度和载流子类别(电子或空穴)决定.但是在磁性导体中，实验测量的霍尔电压不是随外加磁场增强而线性增加的，因此被称为反常霍尔效应.

量子霍尔效应是凝聚态物理发展历史上里程碑式的重要量子现象，1980年，德国物理学家冯·克利钦(K. V. Klitzing)等人发现了整数量子霍耳效应(IQHE)[11]，1982年崔琦等人又在更强的磁场下发现了分数量子霍耳效应(FQHE ) ,二者合称为量子霍耳效应(QHE).冯·克利钦等人观测到，当外加磁场足够强、温度足够低时，霍尔电导不再随着磁场强度线性增加，而是出现了电导平台，其数值是电导量子单位的整数倍，纵向电导为零.在不考虑电子关联与考虑电子关联的体系中，分别可以观测到整数与分数量子霍尔效应. 根据朗道的对称性理论，凝聚态物质中的各种有序态的出现一般都伴随着某种对称性的破缺，同时伴随有局域序参量及其长程关联的出现.而在量子霍尔效应中不存在局域的序参量，对它的描述需要引入拓扑不变量的概念. 不同的拓扑不变量描述的系统具有不同的拓扑态.量子霍尔效应的拓扑不变量就是整数的陈数C(Chern number)，也称之为TKNN数[12]，与霍尔电导紧密相关:

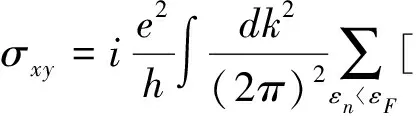
∂xun

(1)

这个整数在数学上称为第一陈数,与系统占据态在布里渊区中的拓扑性质有关：

(2)

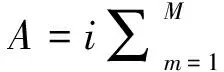
(3)

F是贝里曲率，A是贝里联络，M是占据态的数目.整数量子霍尔系统的拓扑不变量就由第一陈数来表征.拓扑学从此进入了凝聚态物理学的研究领域.由于量子霍尔效应对应的是电荷流，因而可以和现有的电子技术兼容.边缘态可以被看成是理想导线，电阻和能耗极小，可望延展Moore定律的极限[13-15].

量子反常霍尔效应(QAHE)可以看成是不需要外加磁场的量子霍尔效应.它对应于磁性的二维绝缘体，虽然没有外磁场从而没有朗道能级，但其固有的能带结构就携带有非平庸的拓扑特性，从而导致非零陈数的出现.实验中如何实现量子反常霍尔效应，曾经很长时间是凝聚态领域一个极具挑战性和重要物理意义的难题，它需要实验材料同时满足4个条件:(1)二维体系;(2)有自发铁磁序;(3)体态是绝缘态;(4)占据态的能带具有不为零的拓扑陈数. 这是非常苛刻和艰难的.国际上有多个研究团队一直都在努力实现量子反常霍尔效应，直到2013年，薛其坤的实验组和方忠、戴希的理论组合作，终于在磁性原子掺杂的拓扑绝缘体系中首次观察到量子反常霍尔效应(QAHE)[15,16].

量子自旋霍尔效应(QSHE)是最早认识的二维的保持时间反演对称性的拓扑绝缘态，也叫二维的拓扑绝缘体.量子自旋霍尔态(QSHE)可以看成是两套量子反常霍尔态的叠加，而且这两套量子反常霍尔态互为时间反演. 2006年，张首晟研究组独立地提出了一种实现QSHE的一般理论，并预言了HgTe/CdTe超晶格结构可以实现QSHE.2007年，德国的Molenkamp研究组通过实验证实[17]. 量子自旋霍尔效应的边界态受时间反演不变性质的保护，自旋在输运过程中不受非磁性杂质和缺陷的影响，是理想的自旋输运导线.

总体来说，量子霍尔态与拓扑绝缘体的关系及相应的拓扑分类为：(1)量子霍尔态是破坏时间反演的拓扑绝缘态，拓扑不变量为第一陈数.普通绝缘态是第一陈数为零的拓扑平庸态；(2)而对于保持时间反演不变的二维绝缘体，对应的拓扑不变量是Z2数，它分成两类:一类是普通绝缘体，对应Z2=0；另一类是拓扑绝缘体，对应Z2=1；(3)推广到保持时间反演不变的三维系统时，需要用4个Z2拓扑数(1个强拓扑数，3个弱拓扑数)来描述系统的拓扑性质.三维时间反演不变的绝缘体由此可以分为平庸的普通绝缘体、弱拓扑绝缘体和强拓扑绝缘体.其中三维强拓扑绝缘体(如Bi2Se3系列材料)由于在所有方向的表面上都有狄拉克色散形式的表面态[18]而引起了广泛的关注.

2 三维拓扑绝缘体磁电效应与轴子场

上面提到，三维强拓扑绝缘体由于有狄拉克色散形式的表面态，它的边界可以用无质量的狄拉克粒子来描述，所以表面态对电磁场的有效响应的作用量可以表示如下[17]：

(4)

其配分函数是:

(5)

所以有效作用量为：

Seff=-ln det[(∂τ+eA0)+ħvF(ky+eAy)σx-

hvF(ks+eAx)σy-Bzσz]，

(6)

其中A是电磁场的矢势.

三维拓扑绝缘体的表面对电磁场的有效响应对应的作用量为：

(7)

α=e2/ħc≈1/137是精细结构常数，上面就是拓扑场论对三维拓扑绝缘体电磁响应的描述，其有效的相互作用量对应着三维拓扑绝缘体的磁电效应(Magneto-Electric Effect)，即电场可以诱导出磁极化，而磁场也能诱导出电极化.形式上这与QCD的总拉氏量密度中θ真空对应的对称性破缺项很相似:

(8)

因而在场论中与轴子在电磁场中的动力学性质有关，Xiao-Liang Qi 和 Shou-Cheng Zhang等由此给出了凝聚态物理中非高能物理版的轴子[19,20]:

(9)

对应于轴子场，待下面给出高能物理版的轴子由来后再作比较和讨论.

当三维拓扑绝缘体中存在反铁磁相(如Bi2Se3材料中掺入Fe)时，存在幅度和自旋波的激发，会引起轴子场的涨落δθ.此时，考虑轴子场与电磁场的耦合，系统的有效作用量是[19]：

Seff=SMaxwell+Sα-γ-topo+Smassive-axion=

(10)

其中J,v,m分别是自旋波激发的刚度，速度和质量，E,B分别是外电场和磁场，ε是介质的介电常数，μ是磁导率.第二项描述了有质量轴子的动力学.第三项则是轴子与电磁场藕合的拓扑项，其中α是精细结构常数.可以通过这个有效作用量得到如下轴子在电磁场中间的线性运动方程：

(11)

其中c′为光在介电常数为ε的介质材料中光速. 这里光与反铁磁的轴子模式形成了一种新的极化激元一轴子极化激元.其色散关系可以通过有效作用量(10)得到, 这就是Rundong Li和 Shou-Cheng Zhang等提出利用拓扑绝缘体的磁电效应，用轴子极化激元与衰减全反射实验测动力学轴子的理论依据[19].

3 QCD真空的拓扑结构与暗物质轴子模型

量子场论(QFT)是描述微观高速物质世界物理规律的基本理论. 1954年杨振宁和R.L.密尔斯提出非阿贝尔规范场理论[21-26](也叫Yang-Mills理论)是量子场论的一个重要进展，其核心思想是物理基本规律的定域对称性(Local Symmetry).粒子物理的最小标准模型就是建立在规范群SU(3)c×SU(2)L×U(l)Y之上的一个可重整化的Yang-Mill s理论，它可以分为三部分:(1)由费米子描述的物质场; (2)由规范玻色子描述和传递的规范相互作用;(3)为费米子和规范玻色子提供质量的对称性破缺部分.其中描述物质场的费米子由三代的夸克和轻子组成.标准模型中，强相互作用和电弱相互作用都用非阿贝尔规范论描述，量子色动力学(QCD) 就是用来描述强相互作用的.QCD的场方程有非微扰的拓扑孤子―“瞬子(instanton)”解，其基态(即真空)是多重简并的.但因拓扑性质不同, 这些简并的真空可以用不同的拓扑量子数―绕数(winding nuber )来标记，与量子霍尔态引入拓扑量子数的情况非常相似.拓扑量子数―绕数表示为[21-26]：

(12)

这些简并真空的非平庸拓扑结构与量子力学中的周期位势类似，不同的真空之间由势垒隔开，拓扑不同的真空态间的隧穿过程就形成瞬子，或者说瞬子解造成了真空态之间的隧穿透，类似于量子隧穿效应(tunnel effect)[26]. 强相互作用的瞬子即隧穿QCD真空的拓扑孤子.

图1 瞬子导致拓扑性质不同的真空态之间的隧穿Fig.1 |n> vacua change by gauge transformations

瞬子解导致拓扑性质不同的真空态之间的隧穿表示为：

U1|n=|n+1.

(13)

物理的真空必须是规范不变的，由此重新定义QCD的θ真空：

|θ.

(14)

可以证明θ真空是规范不变的：

Uk|θ=

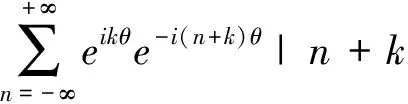
(15)

QCD的总Lagrangian密度表达式为[21]：

(16)

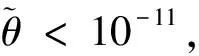
历史上学者们提出了许多理论模型和解释方案，其中 R. D. Peccei 和H. R. Quinn[21-25]理论上引入赝标量场—轴子场的方案被认为是最优美(elegant)的解决方案，他们比粒子物理的最小标准模型(SM)多引入了一个Higgs二重态：

(17)

Higgs场的势为：

(18)

从而理论中有了包含Higgs场位相变换的新的U(1)规范对称性U(1)PQ，在U(1)PQ对称性下，

(19)

事实上这就是U(1)PQ对称性与原来SM中间的U(1)规范对称性的不同之处.Higgs场在如下U(1)PQ变换下不变：

U(1)PQ:Φ1→eiaΓ1Φ1,Φ2→einΓ2Φ2.

(20)

在U(1)PQ对称性变换下,其他夸克场和轴子场的变换为：

(21)

通过U(1)PQ对称性的自发破缺的Higgs机制，把Higgs场按幺正规范表示为：

(22)

ρi,vi是实场，Higgs场的基态-真空期望值不为零:

(23)

意味着U(1)PQ对称性的自发破缺.根据关于对称性和守恒定律的Noether定理，应该有一个赝Goldstone粒子，而且由于有瞬子效应而得到质量.赝标量轴子场就放在Higgs场的相角中，它由Higgs场相位的线性组合得到:

a(x)≡cosθP1(x)+sinθP2(x).

(24)

另一个Higgs场相位的线性组合

(25)

被吸收到标准模型原有的z0玻色子中.

在轴子模型中，轴子U(1)PQ对称性的自发破缺的能标f0是一个很重要的概念，它也叫做轴子的衰变常数. 当fa≪few，即U(1)PQ对称早在电弱相互作用破缺之前就已经破缺了.此时轴子如果存在，其质量很小，与物质(包括电磁场)的耦合非常弱，很难在实验中探测到，所以被形象地统称为“invisible axion”(“看”不见的轴子). 其中讨论最多主要有两种：(1)KSVZ 轴子模型(Kim- Shifman-Vainshtein-Zakharov axion model) ,也叫强子轴子模型(hadronic axion model )，这种轴子不直接与通常的夸克、轻子等相互作用；(2)DFSZ轴子模型(Dine-Fischler- Srednicki-Zhitnitski axion model) ,也叫大统一轴子模型(grand unified theories (GUT) model)，这种轴子可以直接与通常的夸克、轻子等耦合，其中fa≥1012GeV对应的轴子被认为是冷暗物质很好的候选者[21-25].

4 两类轴子探测方法

探测轴子的实验很多，如美国佛罗里达大学(University of Florida)的Pierre Sikivie教授在1983年提出来的微波腔轴子实验探测方法；欧洲核子中心的CERN的太阳轴子望远镜(CAST, CERN Axion Solar Telescope)和日本东京大学的太阳轴子望远镜(Tokyo Axion Helioscope Telescope)方法等等.从物理过程来看，主要是探测轴子与光子的耦合过程[27,28].如R. Cameron等让激光通过强磁场测轴子实验，根据Primakoff效应,线偏振光通过强磁场时,其垂直于磁场的分量(相当于图2中的虚光子)会与磁场相互作用产生轴子,此过程轴子与光子的耦合的费曼图如图2.

图2 激光通过强磁场产生轴子的费曼图Fig.2 Feynman diagram of axion which produced by Laser travel through strong magentic field

按照量子电动力学(QED), 激光束提供的大量光子(实光子γ,如图2)与强磁场(相当于提供虚光子γ*,如图2)相互作用产生轴子a,其相互作用的Lagrangian密度为[22,28]:

(26)

对于拓扑绝缘体，Rundong Li和Jing Wang, Shou-Cheng Zhang等提议的用磁性拓扑绝缘体(TMI)的磁电效应，通过轴子极化激元与衰减全反射实验测动力学轴子[19]的方法详细见参考文献[19].

5 讨论与结论

从上面我们可以看到：

(1)QCD轴子模型起源于强CP问题， 而强CP问题源于QCD的总Lagrangian密度的(16)式CP破缺项，这一项是由QCD的真空拓扑结构导致的. 在轴子探测实验中，轴子与电磁场相互作用的Lagrangian密度为(26)式:

另一方面，由Lagrangian密度与作用量的关系：

(27)

可以得到(10)式三维拓扑绝缘体的磁电响应有效作用量的拓扑项如下：

Seff=SMaxwell+Smasstive-axtion+Sa-γ-topo=

其中对应拓扑项为:

(28)

所以有：

(29)

式(29)中的g′相当于耦合系数，由(28)式的积分结果决定.(29)式对应于轴子场.(26)式与(29)式θ表明三维拓扑绝缘体在电磁场中的响应与轴子在电磁场的耦合相同的根源在于QCD的真空结构与拓扑绝缘体的电子能带结构有相似的拓扑特性；

(2)θ项的具体含义是不同的，(16)式中的θ是QCD真空的标志，不直接代表轴子；而(29)式直接代表轴子场，并且对应于拓扑绝缘体的分类，即θ=0为普通绝缘体，即θ=π对应拓扑绝缘体[19]；

(3)轴子模型起源于强CP问题，也为解决强CP问题, 这是在构造轴子模型的出发点和目的，所以从物理起源上看二者是不同的.(29)式代表三维拓扑绝缘体在电磁场中的响应，实质是它的电子在外场下的动力学行为，由其特殊的能带结构所决定；它与(26)式轴子在电磁场的动力学行为相似，所以这里提到的动力学轴子场也是拓扑绝缘体在外电磁场中耦合响应的结果；

(4)由于invisible axions与周围物质环境的耦合非常弱，因此如果轴子暗物质存在，则它可以轻松透过大多数物质，非常稳定地存在于宇宙空间中.所以三维拓扑绝缘体体内和界面都可以有轴子参与电磁场的耦合，加之二者有相似的动力学响应，因而利用拓扑绝缘体在实验中探测冷暗物质轴子是可能的.但对于提议的用磁性拓扑绝缘体(TMI)测暗物质轴子的实验，其探测的冷暗物质轴子应该是外来的，而非TMI产生的.这样才与探测宇宙中可能存在的冷暗物质轴子的议题相洽.

参 考 文 献

[1] Wolf S A,Awschalom D D,Buhrman R A,et al.Spintronics: A Spin-Based Electronics Vision for the Future[J].Science,2001，294(5546):1488-1495.

[2] Awschalom D D,Flatte M E. Challenges for semi-conductor spintronics [J]. Nat Phys,007,3:153.

[4] Hasan M Z,Kane C L. Colloquium:topological insulators [J].Rev Mod Phys,2010,82:3045-3067.

[5] Zhang S C.Topological states of quantum matter[J].Physics,2008,1:6-8.

[6] Moore J.Topological insulators: the next generation [J].Nat Phys,2009,5:378-380.

[7] Teo J C Y,Kane C L.Majorana fermions and non-abelian statistics in three dimensions [J]. Phys Rev Lett,2010,104: 046401-046404.

[8] Smith A W,Sears R W.The Hall effect in perma lloy [J].Phys Rev,1929,34: 1466-1473.

[9] Hirsch J E.Spin Hall effect[J].Phys Rev Lett,1999,83:1834-1837.

[10] Wunderlich J,Kaestner B,Sinova J et al.Experimental observation of the spin-Hall effect in a two-dimensional spin-orbit coupled semiconductor system [J].Phys Rev Lett,2005,94: 047204-047207.

[11] Klitzing K V,Dorda G,Pepper M.New method for high-accuracy determination of the fine-structure constant based on quantized hall resistance [J].Phys Rev Lett,1980,45: 494-497.

[12] Niu Q,Thouless D J.Nonlinear correction to the quantization of Hall conductance [J].Phys Rev B, 1984,30: 3561-3562.

[13] Essin A M,Moore J E, Vanderbilt D.Magnetoelectric polarizability and axion electrodynamics in crystalline insulators [J]. Phys Rev Lett,2009,102(14)：146805.

[14] 叶 飞，苏 刚.拓扑绝缘体及其研究进展 [J].物理，2010,39: 564-569.

[15] 翁红明,戴 希,方 忠.磁性拓扑绝缘体与量子反常霍尔效应 [J].物理学进展，2014,34: 1-9.

[16] Cui-Zu Chang,Jinsong Zhang,Xiao Feng,et al.Experimental Observation of the (quantum Anomalous Hall Effect in a Magnetic Topological Insulator [J].Science,2013,340(6129):167-170.

[17] Qi X L,Zhang S C..Topological insulators and superconductors [J].Rev Mod Phys,2011,83:1057-1110.

[18] 余 睿,方 忠,戴 希.Z2拓扑不变量与拓扑绝缘体 [J].物理,2011,40(7):462-468.

[19] Rundong Li,Jing Wang,Xiao-Liang Qi, et al.Dynamical axion field in topological magnetic insulators [J]. Nature Physics ,2010,6:284-288.

[20] Qi X L,Hughes T L,Zhang S C.Topological field theory of time-reversal invariant insulators [J].Phys Rev B, 2008,78: 195424-195466.

[21] Wilczek F.Two applications of axion electrodynamics[J].Phys Rev Lett,1987,58:1799-1802.

[22] R.Cameron,G.Cantatore,A.C.Melissinos,et al.Search for nearly massless,weakly coupled particles by optical techniques[J].Phys Rev D,1993,47:3707.

[23] Peccei R D,Quinn H R,CP Conservation in the Presence of Pseudoparticles [J].Phys Rev Lett,1977,38:1440-1443.

[24] Kim J E.Light psedoscalars,particle physics and cosmology [J].Phys Rept,1986,150:1-177.

[25] Kim J E.Weak-interaction singlet and strong CP invariance[J].Phys Rev Lett,1979，43:103-107.

[26] 戴元本.相互作用的规范理论[M].2版.北京： 科学出版社，2006:474-494.

[27] Dine M,Fischle W.Srednicki M.A simple solution to the strong CP problem with a harmless axion[J].Phys Let B，1981，104：199-202 .

[28] Kim J E, Carosi G.Axions and the strong CP problem [J].Rev Mod Phys,2010,82: 557-602.