引入有取向二面角散射的Freeman-Durden分解

闫 剑 李 洋 尹 嫱 洪 文(中国科学院电子学研究所 北京 100190)(中国科学院大学 北京 100190)

引入有取向二面角散射的Freeman-Durden分解

闫 剑*①②李 洋①②尹 嫱①②洪 文①①(中国科学院电子学研究所 北京 100190)②(中国科学院大学 北京 100190)

该文首先考察了当极化SAR方位向与农作物种植行向不一致时，入射电磁波到地表、农作物的二次散射与一般二次散射的区别。其次，为描述这种二次散射，建立了有取向的二面角散射模型，并将该模型引入到Freeman-Durden目标分解中，设计了相应的目标分解算法。最后，选取同一农作物种植区两种航迹的机载全极化SAR数据实现了该分解算法。实验结果证明，对于农作物种植区，改进后的Freeman-Durden分解能提升不同航迹下的极化SAR数据目标分解的一致性。

合成孔径雷达(SAR)；极化；极化目标分解；二面角散射

1 引言

极化目标分解(polarimetric target decomposition)是从全极化 SAR数据解译地面目标散射机制的一类重要方法。极化目标分解可分为相干分解和非相干分解[1]。相干分解适用于单目标Sinclair矩阵S，非相干分解适用于分布式目标的极化协方差矩阵C或极化相干矩阵T。常用的两种非相干目标分解方法是 H-Alpha-A 分解[2]和 Freeman-Durden分解 (以下称F-D分解)[3]。H-Alpha-A分解基于极化协方差矩阵的特征值分解，将3组特征矢量对应为3种散射机制，相应的特征值则代表3种散射机制在目标散射中的权重。由特征值和特征矢量可建立极化熵(H), Alpha角和各向异性度(A)3个变量，分别衡量分布式目标的随机性程度，主散射机制和各向异性度；F-D分解基于极化散射机制，将协方差矩阵 C分成 3项：由小扰动模型(Small Perturbation Model, SPM)[4]建立的面散射项，由地表和植被的菲涅耳系数[4]建立的二次散射项，由随机分布的偶极子簇散射建立的体散射项。

极化 SAR数据敏感于目标的几何特征。对于农用地，地物目标的几何特征主要包括：地形坡度，农作物生长几何形态和农作物种植结构。关于地形坡度对极化目标分解的影响：文献[5]考虑了经过极化取向角(Polarization Orientation Angle, POA)补偿后，F-D三成分分解各分量的变化。文献[6]考虑了引入POA补偿后的四分量分解；关于农作物生长几何形态对目标分解的影响：F-D分解中，植被层由随机分布的偶极子簇构成。Yamaguchi四分量分解则根据不同植被的几何形态，将植被描述成具有不同分布特征的3种偶极子簇。Arii分解[7]中，植被层由多种散射子组合而成，每一种散射子都有特定概率分布密度和整体取向角。

本文将考虑农作物种植行向对 F-D分解的影响。当极化SAR航迹与农作物种植方向不平行时，由地表和农作物构成的二面角的交线不再与极化SAR方位向平行，此时有必要考虑由于种植行向变化造成的二次散射机制变化。本文将建立有取向的二面角散射以描述这种变化，并将其引入到F-D分解当中，完成农作物种植区极化 SAR数据目标分解。第2节分析了当二面角交线与SAR方位向之间存在夹角时，有取向的二面角散射矩阵的形式；第3节将有取向的二面角散射模型引入到F-D分解当中，并建立了相应的分解算法；第 4节利用AgriSAR农作物种植区两种航迹下的全极化机载SAR数据实现了该算法，对比了改进前后的 F-D分解的结果。第5节给出了本研究的结论。

2 有取向的二面角散射

电磁波在农作物种植区的二次散射发生在地表和垂直生长的植被之间。如图1所示，将地表和植被抽象为相互垂直的两个面P1和P2，则农作物种植行向可用两个面的交线方向矢量t来描述。为考察该面P1和P2之间的二面角散射，首先以SAR下视点O为原点，建立地面坐标系(x y z)，其中x指向为极化SAR方位向，z指向为地面法向量，(x y)平面与地表平面P1共面，(y z)平面为SAR入射面。如图1(a)所示，当极化SAR方位向与农作物种植行向平行时，也即x轴方向与交线t方向平行时，SAR入射面与二面角交线t垂直，散射面与入射面共面，此时电磁波二次散射为常见的二面角散射，本文称之为普通二面角散射。如图1(b)所示，当极化SAR方位向x与农作物种植行向t夹角为ϕ时，本文称二面角绕 z轴有取向角ϕ，以下研究有取向的二面角散射模型。需要指出的是，本文中有取向的二面角散射与文献[5]提出的极化面的取向有差别，前者是由于二面角绕z轴旋转造成的二面角散射变化，而后者是由于(x y)平面内地形坡度导致的极化面的偏转，不能直接引用后者的散射模型来描述前者。

先考察图1(a)中普通二面角散射的极化散射矩阵。设SAR入射角为θ1，面P1和P2的介电常数分别为ε1和ε2，则根据文献[8]的研究结果，二面角散射矩阵为：

图1 普通二面角散射和有取向的二面角散射Fig. 1 Normal dihedral scattering and dihedral scattering with oriented angle ϕ

以下将进行有取向的二面角散射建模。如图1(b)中所示，极化电磁波沿波矢量ki入射到面P1，与面P1发生第1次散射后沿波矢量k1入射到面P2，经第2次散射后再沿波矢量ks返回到极化SAR接收天线。其中，第1次散射中的入射角由ki和面的法向量n1决定，第2次散射中的入射角由k1和面P2的法向量n2决定。波矢量k1由入射波矢量和ki和面P1的法向量n1决定。

在入射面(y z)平面内，电磁波入射角为θ1，则入射波矢量可写成

注意到，在普通二面角散射的两次面散射中，极化电磁波入射面和散射面始终共面，即处于(y z)平面上。而在有取向的二面角散射中，由于取向角ϕ导致面P2的法向量发生偏转，因而在面P2上的入射和散射过程都有极化面的偏转。入射过程极化面偏转是指面P1上的散射波投影到以n2和k1构成的第2次散射的入射面上；散射过程极化面偏转是指面P2上的散射波投影到接收天线的极化面上。两次极化面的偏转角φ1和φ2可以按如下公式计算：

考虑第2次散射中两次极化面偏转，则可将有取向的二面角极化散射矩阵写成如下形式：这里BHH和BVV是SPM模型中的Bragg系数，如式(3)所给出。令

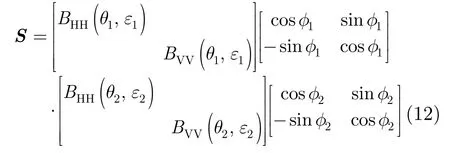
3 引入有取向二次散射的Freeman-Durden分解

首先引用文献[9]给出的面散射和体散射协方差矩阵形式如下：

将式(16)-式(18)中极化协方差矩阵的共同因子化为对应散射机制的权系数，则可将极化 SAR数据C合成的协方差矩阵写成3种散射机制之和

其中Cij为SAR数据极化协方差矩阵的元素，Cvolij为式(18)中体散射协方差矩阵的元素。式(20)构成了引入有取向二面角散射的Freeman-Durden目标分解模型。以下研究对应的目标分解算法。

由方程组式(20)中第 2式和第 5式得到：C12/conj(C23)=p/r 。令t3= C12/conj(C23)= p/r；于是方程组可写成

将第2式代入第4式中，第5式代入第1, 3, 6式中，有

将其中第1, 2, 4式变形为线性方程组，第3式写成判别条件：

式(26)中方程组的解法为：迭代β，求解 A/q, B/q, r/q, 再利用式(26)中判别条件检验求解准确度。得到解后，按如下公式计算3种散射机制的功率分量：

综上，建立算法流程如下：

(1) 线性方程式(26)中代入极化 SAR数据协方差矩阵C和体散射模型Cv；

(2) 初始化β，解线性方程式(26)，得到最优β, A/q, B/q, r/q；

(3) 由式(28)计算fd|q|2；

(4) 由式(29)计算fs, fv；

(5) 由t3= C12/conj(C23)计算t3；

(6) 利用式(27)计算3种散射机制的功率。

4 数据处理及讨论

本文利用AgriSAR数据集第12次数据和第13次数据验证本文提出的目标分解模型。两次数据由L波段机载全极化E-SAR系统采集，采集时间分别为2006年7月5日和7月6日，采集地点位于德国东北部Gormin农场[10]。如图2所示，第12次数据和第13次数据分别覆盖GorminⅠ和Gormin Ⅱ两个区域。GorminⅠ航迹为东西向，Gormin Ⅱ航迹为西南-东北方向，在图2中分别用红色箭头指出。GorminⅠ和 Gormin Ⅱ在图 2中所示的菱形区域重叠，本文选取图2中黑色矩形框区域作为考察区域。该区域包含222号，140号，230号3块样地，分别种植玉米、油菜和小麦，生长情况如图3所示。在两种飞行航迹下，极化 SAR方位向与农作物种植方向之间会呈不同的夹角，电磁波与地表和植被之间二面角散射的取向会因此不同，以下将研究航迹变化对F-D分解结果的影响。为了避免地形坡度导致的极化取向角偏转的影响，本文对考察区域的极化 SAR数据作了极化取向角补偿(Polarization Orientation Angle Compensation, POAC)。

图4给出在考察区域AgriSAR第12次和第13次数据经POAC后的Pauli基伪彩色图像。两次数据采集时间相隔1天，两幅图像对应样地上植被的生长形态变化可忽略不计。但从两幅伪彩色图像来看，3块样地的极化特性因航迹改变而有显著不同。事实上，极化取向角补偿只能消除由坡度带来的极化面偏转效应，而不能减弱因航迹变化对地物散射机制变化的影响。

图5(a1)和图5(a2)分别给出了经POAC后的第12次数据和第13次数据经典F-D分解伪彩色图。红、绿、蓝三色分别对应二面角散射功率(pd)、体散射功率(pv)和表面散射功率(ps) 的权重。可以看出，差异最明显的是222号样地，在第12次数据中以体散射为主导，而在第13次数据中以二面角散射为主。其次是140号样地，第12次数据中二面角散射权重要高于第13次数据。230号样地的两次分解结果差异不大，但仍可以看出二者都以表面散射为主导，但第13次数据中表面散射更多一些。由于两次数据采集时间相隔1天，相同样地农作物生长形态变化可忽略不计。但由于航迹变化影响，导致二者的F-D目标分解结果出现显著差异。如果将该分解结果应用于极化目标分类，则相同农作物可能被分到不同的类别。

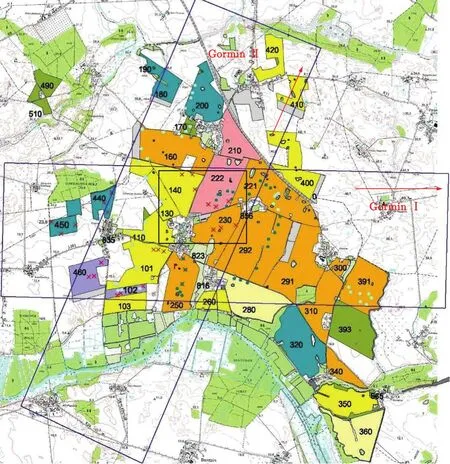
图2 AgriSAR第12次数据覆盖区域(GorminⅠ)和第13次数据覆盖区域(GorminⅡ)Fig. 2 The 12th coverage (GorminⅠ) and the 13th coverage (GorminⅡ) of AgriSAR data

图5(b1)和图5(b2)分别给出了经POAC后第12次数据和第13次数据应用本文提出的改进后的F-D分解结果。整体上可以看出，改进的F-D分解较好地提升了不同航迹下极化数据目标分解一致性。为了更直观描述改进前后的F-D分解结果一致性的对比，本节对图5中每块样地选取窗口，将窗口中像素点对应的3种散射机制功率写成三元坐标数组(ps, pd, pv)，形成如图 6所示的散点图。图 6中左边3个子图分别对应3种样地应用经典F-D分解结果的一致性，右边3个子图对应3种样地应用本文改进的F-D分解结果的一致性。每个子图中，蓝色点和红色点分别代表两种航迹下的分解结果。

以图6(b1)和图6(b2)为例，图6(b1)显示的是222号样地SAR数据应用经典F-D分解的结果，图6(b2)显示的是222号样地SAR数据应用改进后的F-D分解的结果。其中蓝色代表GorminⅠ航迹下的分解结果，红色代表Gormin Ⅱ航迹下的分解结果。两种颜色星号重合程度越高，则代表目标分解一致性越好。不难看出，图6(b2)相比图6(b1)，有更高的一致性。为了更精确描述图6中不同航迹下极化 SAR数据的目标分解结果一致性程度，引入如下参量：

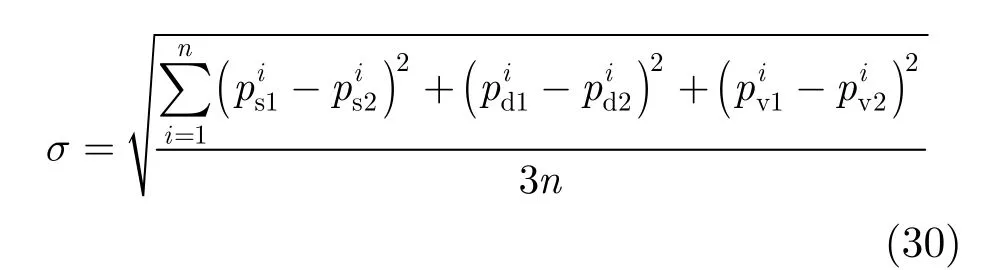
如表1所示，求图6中的6幅子图的σ值，对经典F-D和改进的F-D分解结果一致性作定量对比。可以看出，改进的F-D分解能够减小σ值，即减小不同航迹下分解结果的差异，提高不同航迹下分解结果的一致性。

图3 3块样地农作物生长状况：140(油菜)，222(玉米)，230(小麦)Fig. 3 Growth of the three test sites: 140(rape), 222(maize), 230(wheat)

图4 Pauli基极化SAR图像Fig. 4 Polarimetric SAR images on Pauli basis

图5 经典F-D分解结果及改进F-D分解结果Fig. 5 Decomposition results using classical F-D and decomposition results using improved F-D

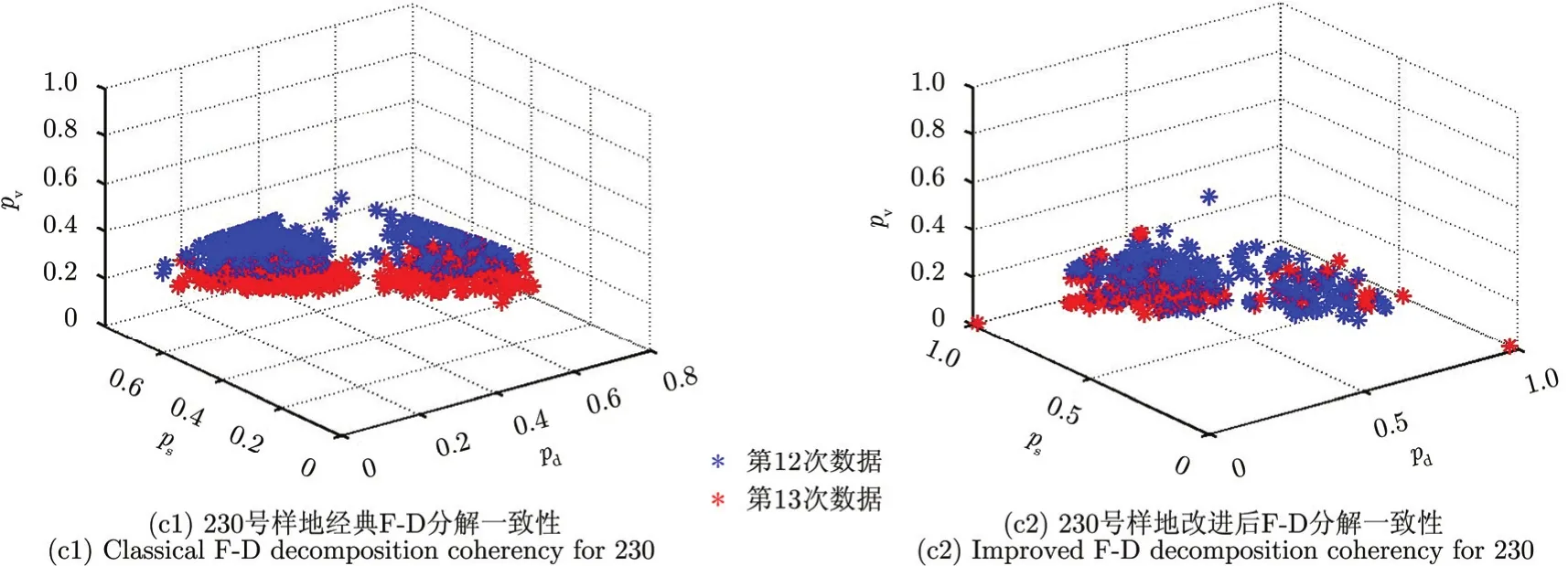
图6 不同航迹下的极化SAR数据目标分解一致性对比Fig. 6 Pol-SAR data decomposition coherency between different flight tracks

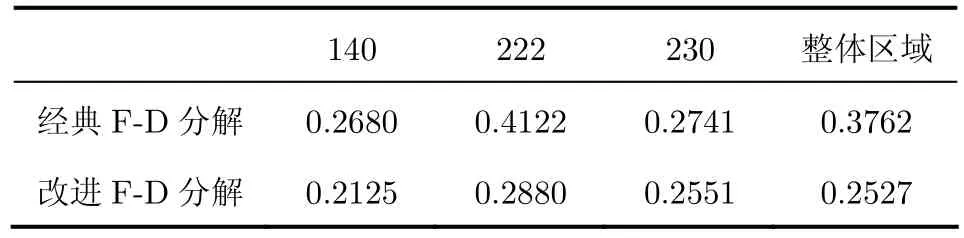
表1 经典F-D分解和改进后F-D分解结果的σ值对比Tab. 1 Decomposition coherence σ comparison: classical F-D vs. improved F-D

222号样地不同航迹下分解一致性的改善效果最明显。从图3可看出， 222号样地种植的玉米有比较规则的种植行向，并且冠层的郁闭程度低，电磁波从地面到玉米植株的二面角散射比较强。当极化 SAR方位向偏离植被种植行向时，有取向的二面角散射会增强，经典F-D分解将这一部分功率划分到体散射项或表面散射项。本文改进的F-D分解能准确处理有取向二面角散射功率，因此能较大地提高222号样地目标分解的一致性。

140号样地不同航迹下分解一致性改善程度相对较低。如图3所示，140号样地种植的油菜种植行向不明显，并且冠层郁闭程度较高，具有高度随机性。140号样地以体散射为主要散射机制，二面角散射为次要散射机制。当极化 SAR方位向偏离油菜种植行向时，有取向的二面角散射功率在经典F-D分解中被分到体散射项。改进的F-D分解将该部分功率分到二面角散射。但该样地二面角散射权重较低，因此改进的F-D分解目标分解一致性改善程度相对较低。

230号样地不同航迹分解一致性改善程度最低。如图3所示，该样地农作物为生长成熟期的小麦，由于L波段电磁波难以穿透厚密的麦穗层，因此230号样地以小麦冠层表面散射为主散射机制，体散射为次要散射机制，二面角散射权重很低。在该样地，改进的F-D分解和经典F-D分解结果差别很小，分解一致性改善不明显。

5 结论

本文考虑极化 SAR方位向变化对二次散射的影响，建立了有取向的二面角散射模型，并将其引入到Freeman-Durden分解中，建立了相应的分解算法。本文选取了具有两种航迹的农作物种植区极化 SAR数据实现了该算法。实验结果证明，相比于经典的F-D分解，本文改进的F-D分解能较大地提升考察区域不同航迹下极化 SAR数据目标分解结果的一致性。在考察区域内，以二面角散射为主散射机制的玉米种植区目标分解一致性提升最显著，以二面角散射为次要散射机制的油菜种植区目标分解一致性提升程度相对较低，而二面角散射机制权重很低的小麦种植区目标分解一致性提升程度很低。

[1] Lee J S and Pottier E. Polarimetric Radar Imaging: from Basics to Applications[M]. Boca Raton, London, New York: CRC Press, 2009: 179-225.

[2] Cloude S R and Pottier E. An entropy based classification scheme for land applications of polarimetric SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(1): 68-78.

[3] Freeman A and Stephen L D. A three-component scattering model for polarimetric SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 963-973.

[4] Ulaby F T, Moore R K, and Fung A K. Microwave Remote Sensing: Active and Passive, VolumeⅠ[M]. Reading, Massachusetts, Addison-Wesley, 1982.

[5] Lee J S, Dale L S, and Thomas L A. Polarimetric SAR data compensation for terrain azimuth slope variation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2153-2163.

[6] Yamaguchi Y, et al.. Four-component scattering model for polarimetric SAR image decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(8): 1699-1706.

[7] Van Z, Jakob J, Motofumi A, et al.. Model-based decomposition of polarimetric SAR covariance matrices constrained for nonnegative eigenvalues[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(9): 3452-3459.

[8] Cloude S R and Pottier E. A review of target decomposition theorems in radar polarimetry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(2): 498-518.

[9] Yamaguchi Y, et al.. Four-component scattering power decomposition with rotation of coherency matrix[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2251-2258.

[10]European Space Agency, German Aerospace Center, et al.. AGRISAR 2006, Agricultural Bio-/Geophysical Retrievals from Frequent Repeat SAR and Optical Imaging[R]. 2008.

Freeman-Durden Decomposition with Oriented Dihedral Scattering

Yan Jian①②Li Yang①②Yin Qiang①②Hong Wen①①(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)②(University of Chinese Academy of Sciences, Beijing 100190, China)

In this paper, when the azimuth direction of polarimetric Synthetic Aperature Radars (SAR) differs from the planting direction of crops, the double bounce of the incident electromagnetic waves from the terrain surface to the growing crops is investigated and compared with the normal double bounce. Oriented dihedral scattering model is developed to explain the investigated double bounce and is introduced into the Freeman-Durden decomposition. The decomposition algorithm corresponding to the improved decomposition is then proposed. The airborne polarimetric SAR data for agricultural land covering two flight tracks are chosen to validate the algorithm; the decomposition results show that for agricultural vegetated land, the improved Freeman-Durden decomposition has the advantage of increasing the decomposition coherency among the polarimetric SAR data along the different flight tracks.

Synthetic Aperture Radar (SAR); Polarization; Polarimetric target decomposition; Dihedral scattering

TP753

A

2095-283X(2014)05-0574-09

10.3724/SP.J.1300.2014.14057

2014-03-25收到，2014-04-08改回；2014-08-29网络优先出版NHTRDPC (2011AA120401)资助课题

*通信作者： 闫剑 jian.shi.yan@gmail.com

闫 剑(1984-)，男，湖北黄冈人，中国科学院电子学研究所在读博士生，研究方向为极化正演模型和极化SAR数据参数反演。

E-mail: Jian.shi.yan@gmail.com

李 洋(1983-)，男，北京人，中国科学院电子学研究所助理研究员，在读博士生，研究方向为极化SAR信息处理与应用。

E-mail: liyang@mail.ie.ac.cn

洪 文(1968-)，女，中国科学院电子学研究所研究员，博士生导师，研究方向为雷达信号处理理论、SAR成像算法、微波遥感图像处理及其应用等。

E-mail: whong@mail.ie.ac.cn