基于独立分量分析法的稀疏阵列穿墙成像雷达直达波干扰抑制

张 驰 李悦丽 周智敏

(国防科技大学电子科学与工程学院 长沙 410073)

基于独立分量分析法的稀疏阵列穿墙成像雷达直达波干扰抑制

张 驰*李悦丽 周智敏

(国防科技大学电子科学与工程学院 长沙 410073)

强的墙体直达波严重干扰了穿墙成像雷达的目标信号，而采用稀疏阵列天线的穿墙雷达，由于通道数少使得基于单次快拍数据分离目标和干扰信号难度更大。该文根据实际通道每次收发获取的距离像存在微弱起伏的现象，提出一种采用单通道多次快拍数据建立观察矩阵，并使用独立分量分析分离直达波与目标信号的方法。仿真及实测数据处理结果表明，在低信杂比(-30 dB)的条件下，该方法仍可有效分离目标和干扰成分，达到较好的直达波抑制效果。

穿墙成像雷达(TWIR)；直达波抑制；独立分量分析(ICA)；稀疏阵列

1 引言

穿墙成像雷达(Through-the-Wall Imaging Radar, TWIR)可对墙后态势进行感知，因而在军事、反恐、救灾等领域有重大的应用前景，近年来受到人们的广泛重视[1,2]。如何消除墙体直达波对目标信号造成的严重干扰，是TWIR需要解决的关键问题之一。对于静止目标，一种直接的方法是事先录取背景信号，然后采用背景相消法去除墙体直达波在内的静止干扰[3]，但该方法的局限性在于需要获得成像区域的先验知识。以奇异值分解(Singular Value Decomposition, SVD)、主元分析(Principal Component Analysis, PCA)为代表的子空间法，无需场景的先验知识，按照奇异值(或特征值)的大小，将原始信号投影到不同的子空间中，在一定程度上可以达到抑制干扰的目的[4,5]。然而在信杂比较低的情况下，弱目标的子空间特征往往无法突显。子空间法的本质是把原始信号分解为互不相关的分量，相比之下，独立分量分析法(Independent Component Analysis, ICA)假设原始信号由若干统计独立的源信号线性混合而成，这在许多应用中更符合信号的本质结构[6]，因而能更有效地提取目标信号。

单收发系统的TWIR常采用合成孔径模式，通过扫描获取 B-scan(距离向-方位向 2维观察数据)矩阵进行杂波抑制[4－7]。而采用阵列天线的TWIR，则多采用单发多收或多发多收模式，通过快拍方式(指雷达系统完成一次收发通道的遍历)由各收发通道对场景进行观察[8,9]。其阵元的稀疏分布将导致观察信号的欠缺，这使得单次快拍难以获取足够的观察信号用于分离其中目标和干扰分量。

针对上述问题，本文首先推导了1维距离像的形成过程及其数学表达，引入了ICA数据模型。之后分析了实际通道每次收发获取的信号存在微弱起伏的现象，并研究了 ICA对确定性源信号的适用性，在此基础上提出一种采用单通道多次快拍数据建立观察矩阵，使用ICA分离直达波与目标信号的方法。仿真及实测数据表明，在信杂比低至-30 dB的情况下，该方法仍可分离目标和直达波干扰，解决了稀疏阵列 TWIR因单次快拍观察信号不足造成的无法有效提取墙后目标的问题。

2 1维距离像形成

假设稀疏阵列 TWIR采用步进频连续波(Stepped-Frequency Continuous Wave, SFCW)体制，其频点数为N，则阵列天线第l个收发通道，在第k个频点发射的子脉冲为[10]：

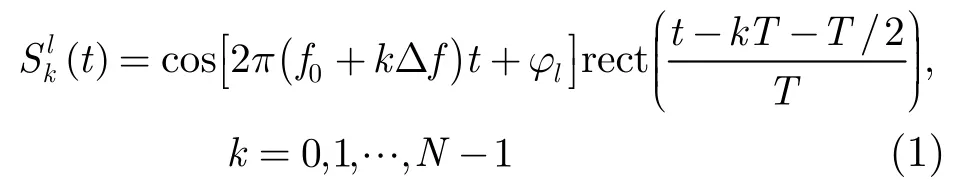
其中 T,f0和Δf分别为子脉冲持续时间、初始频率和频率步进增量；ϕl为通道l初始相位(不失一般性，设 ϕl=0)；矩形函数为：

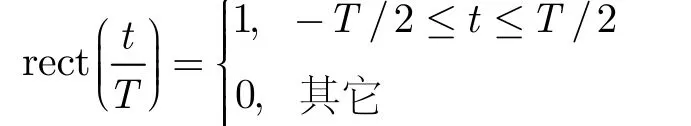
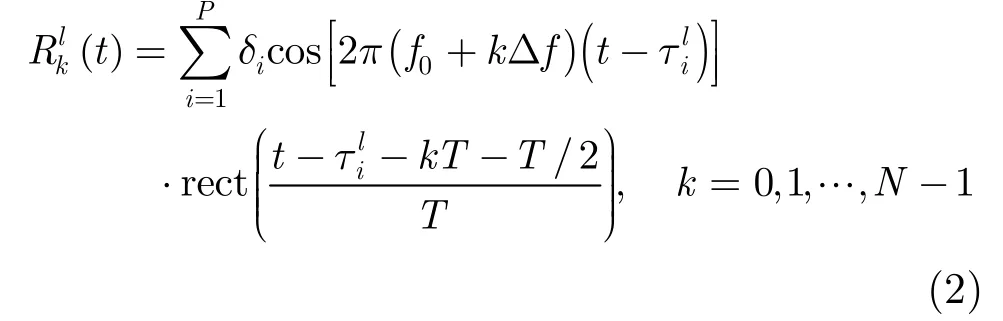
经理想解调，对输出的复信号在其中心处进行采样的结果为[11,12]：

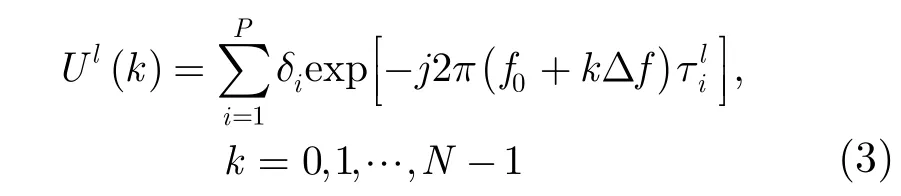
若将Ul(k)视为频域样点，则对所有频点构成的序列做N点逆离散傅里叶变换(Inverse Discrete Fourier Transform, IDFT)，可得到理想情况下通道l的1维距离像[12]：

假设墙体是匀质的，则其前表面也可等效为理想散射点[11]，那么Hl(n)中直达波分量可表示为(n),d∈{1 , 2, … , P }。由于实际中直达波能量远大于目标散射点回波能量，且墙体会对后者造成较大衰减[13]，这使得直达波分量往往将目标分量“淹没”。为了有效提取目标信号，抑制直达波干扰，首先需要对Hl(n)中各分量进行有效分离。

3 ICA模型

ICA作为一种盲源分离方法[14－16]，近年来被引入到TWIR领域中。ICA假设观察变量是若干统计独立的源变量线性混合而成，并依据非高斯性最大化准则，从观察变量中估计出各源变量。其基本模型如下[14]：

由于实际中只能获取各随机变量的采样，若采样数为N，则式(6)，式(7)中X和S分别扩展为M×N维和P×N维采样矩阵，其每一行,分别表示N点源信号和观察信号，并且：

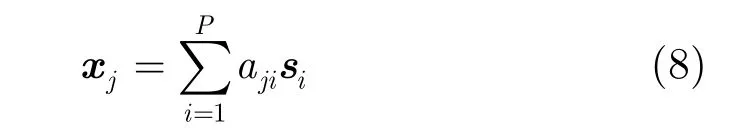
其中aji表示矩阵A的元素。由式(6)和式(7)可知，上述模型成立的前提是M,N和P存在以下关系：

其中rank表示矩阵的秩。由于通常信号的采样数较大，于是有 min(M , N)=M ≥ P 。以上关系说明，ICA只能求解不多于观察信号数量的源信号。此外，由于S,A均未知，使得S中各源信号si的幅度及次序具有模糊性[15]。

4 稀疏阵列的ICA方法

4.1 距离像起伏分析

在理想情况下，只要收发通道位置确定且目标静止，每次快拍获取的Hl(n)是相同的，并不能增加有效的观察信号。但是，我们注意到在实际雷达系统中，即使是单一收发通道的距离像也会受系统相位漂移、杂波环境变化、多路径等多种因素的影响[17]，使其在每次收发中存在起伏。图1为对实际TWIR系统某通道多次收发获取的距离像在固定距离单元进行取样并去除均值的结果(图中一条曲线对应一个距离单元)。其中横轴为收发次数，纵轴表示幅度，n为距离单元编号。可以看出在每一次收发中，不同距离单元处Hl(n)均存在微弱起伏(一般

在均值的0.1%左右)。这样可将通道l第j次收发获取的距离像写作Hlj(n)。并且通过比较图 1(a)与图1(b)可知相邻距离单元的变化趋势类似，而相距较远的则差异较大，由于Hlj(n)的能量主要集中在各的峰值处，于是仅考虑各峰值处的变化，可将式(5)改写为：

4.2 ICA分离确定性信号原理

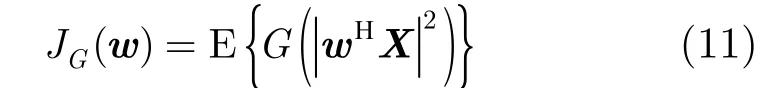
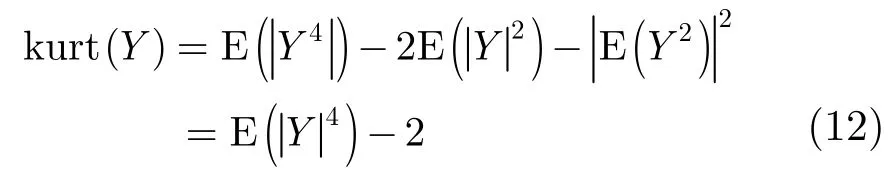
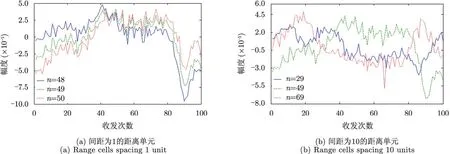
图1 距离像起伏Fig. 1 Fluctuation of range profile

在E{|wHX|2}=1的约束下，ICA算法通过迭代获取JG的极值点wopt，以求得源信号wHoptX，其迭代步骤如下[16]：

步骤1 任意选择初始权向量w0；

步骤2

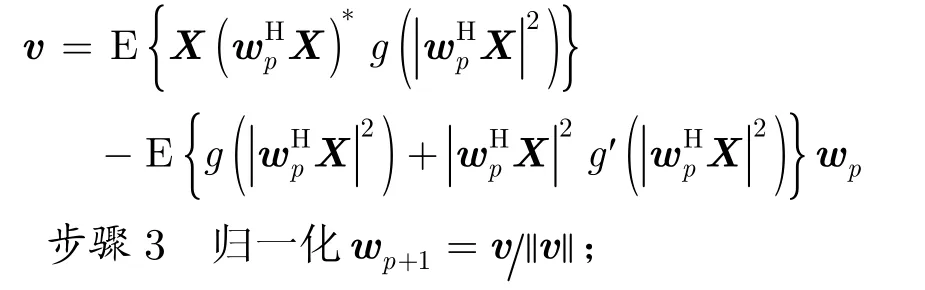
如第3节所述，实际X为观察信号的采样矩阵，根据各态历经性假设，以上迭代过程中各统计量均由时间平均进行计算[19]，即E(⋅)≈，其中算子表示时间平均。进一步由式(6)可知 wHX=wHAS= zHS，可见，即使S为确定性信号，在时间平均的意义下，上述求解过程依然成立，但条件是(表示由时间平均计算的峰度)不能为 0[16]，否则极值点无法求取。另外，当==…=时，算法可能得到错误的结果[19]。

4.3 仿真分析

表1 源信号及混合矩阵参数Tab. 1 Parameters of source signals and mixture matrix

图2(a)，图2(d)，图2(g)为s1,s2峰值位置不同时的源信号图(实际计算时采用的 IDFT点数大于频点数，使得源信号峰值幅度小于1)。图2(b)，图2(e)，图2(h)为对s1,s2乘以混合系数并叠加后得到的观察值x1,x2，注意到s2成分几乎被s1淹没。图2(c)，图2(f)显示经过ICA处理后，相比混合之前，除幅度发生变化外，s1,s2均被有效分离，这说明所提方法具有可行性。但图 2(i)结果显示当目标位置较近时，分离后的s1,s2产生畸变，峰值出现重叠成分，这是由于当Δn趋于0时，,趋同造成的。

4.4 基于ICA的墙体直达波抑制流程

实际应用时可通过M(M＞P)次快拍，使得每个通道l( l=1,2,… ,Q(Q -1))均获取足够观察信号构成观察矩阵 Xl，并通过ICA求得各 Xl中的源信号Sl及混合矩阵 Al。依据式(6)三者满足以下关系：

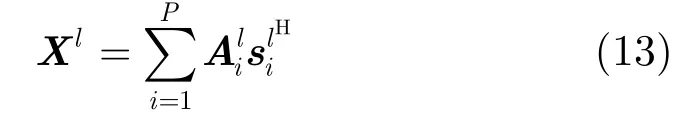
图2 si峰值位置不同时ICA分离结果Fig. 2 Results of ICA when locations of peak of si differ

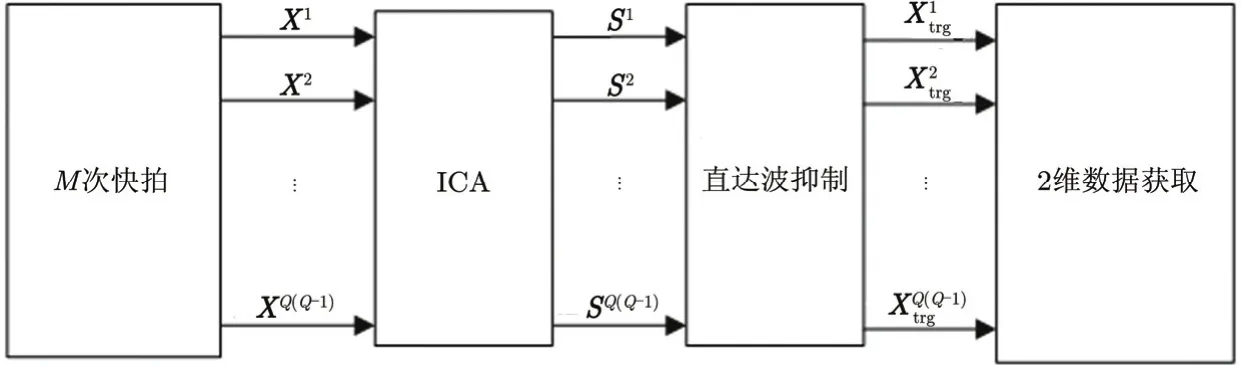
图3 基于ICA的稀疏阵列直达波抑制方法流程图Fig. 3 Flow chart of wall clutter mitigation for sparse array antenna based on ICA

5 实测数据分析

实验使用4块Vivaldi平板天线间隔均匀设置为 3 m长的稀疏天线阵列。一次快拍采取顺序单发多收工作模式，即从阵元1到阵元4，任意时刻只有1个天线发射，余下3个天线顺序接收。因此，雷达系统共有 12个收发通道。发射信号采用SFCW体制，扫频范围为317～1815 MHz，频率步进增量为2 MHz，共750个频点。实验系统参数如表2。

表2 雷达系统参数Tab. 2 Parameters of radar system

实验场景以及坐标系设置如图4所示，其中阴影部分均为混凝土墙。实验中天线阵列放置在左侧空房间中，电磁波需穿透墙A，对墙后3.2 m×7 m的房间进行成像。阵列与墙A平行并与其前表面相距6.25 m，墙体厚度为0.35 m。目标为一30 cm三面角，放置在墙后房间中轴线上，距离墙A后表面2 m处，目标距离地面1 m，与天线阵列处于同一水平面。

首先在不放置目标的情况下对成像区域进行一次快拍，以获取各通道的背景干扰。之后将目标放置在指定位置进行50次快拍。在有目标的情况下，某次快拍通道1(阵元1发射阵元2接收)获取的成像区域距离像如图5(a)所示。在直达波以及其它杂波的严重干扰下，距离像中目标分量几乎不可见。从中减去该通道的背景干扰后，可观察到目标距离像，如图5(b)所示，其峰值功率与图5(a)中直达波峰值功率之比约为-30 dB。

之后使用本文提出的方法，对50次快拍中各通道获取观察矩阵 Xl进行ICA处理，得到 Al及Sl。同样以通道1为例，经分解后的 X1中第20行 x1,20中部分信号分量如图6所示。可以看到图6(c)中分量3为目标分量。而由于直达波峰值位于第6个距离单元附近(图5(a)所示)，由此可判定图6(a)中分量1是直达波分量，可将其去除。此外图6中还存在着其它信号分量，这是由多路径信号以及周围环境杂波等干扰造成的，这需要进一步的检测方法将其与目标分量予以区分。以上结果说明ICA可有效分离各通道观察信号中的目标和干扰分量。

在去除干扰后，取第20次快拍对应的2维矩阵B20，利用后向投影(BackProjection, BP)算法进行成像的结果如图7所示。其中图7(a)为对原始数据进行成像的结果，在严重的直达波干扰下几乎无法从中获取目标的信息。而采用本文方法处理后，成像结果中出现了目标成分，如图7(b)所示。图7(c)，图 7(d)分别为对单次快拍数据进行 ICA以及采用SVD进行直达波抑制后的图像(具体方法可参考文献[6,11])，可以看到经过以上方法处理后，从图像中仍然无法分辨出目标。通过计算图像信杂比进一步评价各方法的效果，其计算式为[20]：

式中，A1为图像中目标信号的分布区，N1为区域A1中的数据点数；A2为包含目标在内的杂波分布区，N2为区域A2中的数据点数；为相应像素点的强度。这里选取以目标为中心0.5 m×0.3 m的矩形区域作为A1，(如图7(b)中红色方框所示)，整个图像作为A2，各图像信杂比计算的结果如表3所示。

图4 实验场景Fig. 4 Experimental scene

图5 通道1及目标距离像Fig. 5 Range profile of channel 1 and the target

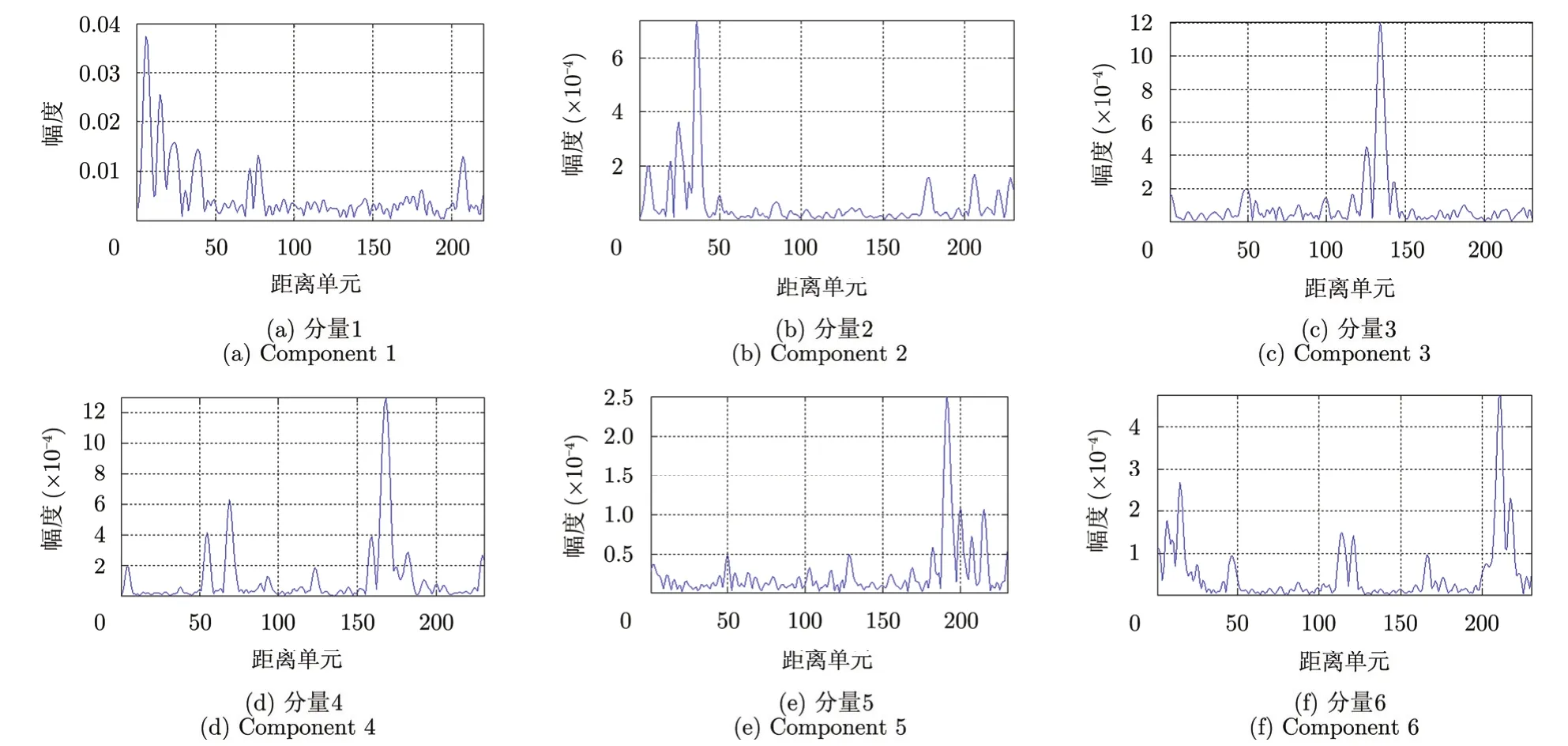
图6 部分信号分量Fig. 6 Parts of signal components

图7 BP成像结果Fig. 7 Results of BP imaging

表3 不同图像信杂比Tab. 3 Signal-to-clutter ratio of different images

相比不做任何处理的情况，使用 SVD算法降低了图像的信杂比，这是由于本实验的阵列配置和收发模式，使得墙体子空间和目标子空间存在较大交叠[11]，导致算法在去除墙体干扰的同时不可避免地损失较多目标能量。而直接使用单次快拍数据进行ICA，解得的分量混合了各通道的直达波和目标信号，基于类似的原因该方法同样降低了图像的信杂比。相比之下，本文方法有效地分离了每个通道中的干扰和目标分量，较好地抑制了直达波，提高了图像的信杂比。

6 结论

针对稀疏阵列单次快拍观察信号不足的问题，本文提出采用单通道多次快拍数据建立观察矩阵，使用ICA分离直达波与目标信号的方法。仿真和实验结果证明，该方法可有效提取目标分量，达到较好的直达波抑制效果。对于实测数据中存在的残余干扰问题，需要研究进一步的检测手段将其与目标成分进行区分，以去除由多路径信号以及周围环境杂波产生的虚假目标。

[1] Baranoski E J. Through-wall imaging: historical perspective and future directions[J]. Journal of the Franklin Institute, 2008, 345(6): 556-569.

[2] Amin M G and Ahmad F. Through-the-Wall Radar Imaging: Theory and Applications[M]. Oxford: E-Reference Signal Processing, Elsevier, 2013.

[3] Debes C, Amin M G, and Zoubir A M. Target detection in single-and multiple-view through-the-wall radar imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(5): 1349-1361.

[4]Tivive F H C, Bouzerdoum A, and Amin M G. An SVD-based approach for mitigating wall reflections in through-the-wall radar imaging[C]. IEEE Radar Conference (RADAR), Kansas City, USA, 2011: 519-524.

[5] Kabourek V, Černý P, and Mazánek M. Clutter reduction based on principal component analysis technique for hidden objects detection[J]. Radio Engineering, 2012, 21(1): 464-470. [6] Gaikwad A N, Singh D, and Nigam M J. Application of clutter reduction techniques for detection of metallic and low dielectric target behind the brick wall by stepped frequency continuous wave radar in ultra-wideband range[J]. IET Radar, Sonar & Navigation, 2011, 5(4): 416-425.

[7] Karlsen B, Sorensen H B, Larsen J, et al.. Independent component analysis for clutter reduction in ground penetrating radar data[C]. International Society for Optics and Photonics, Orlando, USA, 2002: 378-389.

[8] Browne K E, Burkholder R J, and Volakis J L. Through-wall radar imaging system utilizing a light-weight low-profile printed array[C]. Proceedings of the Fourth European Conference on Antennas and Propagation (EuCAP), Barcelona, Spain, 2010: 1-5.

[9] Gu F, Chi L, Zhang Q, et al.. Single snapshot imaging method in multiple-input multiple-output radar with sparse antenna array[J]. IET Radar, Sonar & Navigation, 2013, 7(5): 535-543.

[10]Cui G, Kong L, and Yang X. Reconstruction filter design for stepped-frequency continuous wave[J]. IEEE Transactions on Signal Processing, 2012, 60(8): 4421-4426.

[11]Tivive F H C, Amin M G, and Bouzerdoum A. Wall clutter mitigation based on eigen-analysis in through- the-wall radar imaging[C]. IEEE 17th International Conference on Digital Signal Processing (DSP), Corfu, 2011: 1-8.

[12]Wehner D R. High Resolution Radar[M]. Norwood, MA, Artech House, 1987: 197-234.

[13]Jia Y, Kong L, Yang X, et al.. Multi-channel throughwall-radar imaging based on image fusion[C]. IEEE Radar Conference (RADAR), Kansas City, USA, 2011: 103-105.

[14]Hyvarinen A. Fast and robust fixed-point algorithms for independent component analysis[J]. IEEE Transactions on Neural Networks, 1999, 10(3): 626-634.

[15]Hyvärinen A and Oja E. Independent component analysis: algorithms and applications[J]. Neural Networks, 2000, 13(4): 411-430.

[16]Bingham E and Hyvärinen A. A fast fixed-point algorithm for independent component analysis of complex valued signals[J]. International Journal of Neural Systems, 2000, 10(1): 1-8.

[17]Du L, Liu H, Bao Z, et al.. A two-distribution compounded statistical model for radar HRRP target recognition[J]. IEEE Transactions on Signal Processing, 2006, 54(6): 2226-2238.

[18]Forootan E and Kusche J. Separation of deterministic signals using independent component analysis (ICA)[J]. Studia Geophysica et Geodaetica, 2013, 57(1): 17-26.

[19]Kirimoto T, Danial K, Amishima T, et al.. Performance analysis of independent component analysis to separate mixtures of complex sinusoidal signals[C]. IEEE SICE Annual Conference, Tokyo, 2008: 3424-3430.

[20]Xu Xiao-yin and Miller E L. Entropy optimized contrast stretch to enhance remote sensing imagery[C]. IEEE 16th International Conference on Pattern Recognition, Quebec, Canada, 2002: 915-918.

张 驰(1990–)，男，四川成都人，现为国防科技大学电子科学与工程学院硕士研究生，主要研究方向为穿墙成像雷达信号处理。

E-mail: finderzc@aliyun.com

李悦丽(1973–)，女，湖南浏阳人，博士，现为国防科技大学电子科学与工程学院副教授，获国家科技进步二等奖 1项，部委科技进步一、二等奖各1项，主要研究方向为合成孔径雷达成像以及实时信号处理系统实现。

周智敏(1957–)，男，山东潍坊人，现为国防科技大学电子科学与工程学院教授，博士生导师，主要研究方向为新体制雷达系统与技术。

Wall Clutter Mitigation in Through-the-Wall Imaging Radar with Sparse Array Antenna Based on Independent Component Analysis

Zhang Chi Li Yue-li Zhou Zhi-min
(College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

For Through-the-Wall Imaging Radar (TWIR), wall clutter is critical for detecting target signals behind a wall. For a system with a sparse antenna array, the lack of observation channels makes it more difficult to separate the target signals and wall clutter. On the basis of fluctuation of the range profile in real transmit/receive channels, this paper proposes to use Independent Component Analysis (ICA) on multiple down-range observations of each transmit/receive channel to remove the wall clutter. The simulation and experimental results show that the proposed method effectively separate target and clutter components, even though the signal-to-clutter ratio is only -30 dB.

Through-the-Wall Imaging Radar (TWIR); Wall clutter mitigation; Independent Component Analysis (ICA); Sparse array antenna

TN951

A

2095-283X(2014)05-0524-09

10.3724/SP.J.1300.2014.14066

2014-04-04收到，2014-06-05改回；2014-09-01网络优先出版国家自然科学基金(61302146)资助课题

*通信作者： 张驰 finderzc@aliyun.com