基于改进的ZMNL和SIRP的K分布杂波模拟方法

朱洁丽 汤 俊

(清华大学电子工程系 北京 100084)

基于改进的ZMNL和SIRP的K分布杂波模拟方法

朱洁丽*汤 俊

(清华大学电子工程系 北京 100084)

零记忆非线性变换(ZMNL)法和球不变随机过程(SIRP)法是模拟 K分布杂波的两种常用方法。针对传统ZMNL方法中形状参数(半)整数化所导致的杂波模拟偏差问题，该文提出采用增加Gamma分布生成支路的方法进行改进，改进后的方法能够模拟任意形状参数的K分布杂波；针对传统SIRP方法运算量较大的问题，给出了一种改进的调制变量产生方法，该方法能够避免求解非线性方程，极大地降低了运算量，提高了仿真速度。仿真结果验证了改进方法的有效性。

K分布；雷达杂波；相关；相干

1 引言

杂波是制约雷达目标检测和跟踪性能的主要因素之一，因此对于杂波特性的研究及杂波模拟也始终是雷达领域的研究热点。目前常用的杂波幅度分布模型有瑞利分布、对数正态分布、韦布尔分布和K分布等。由于K分布能较好地描述多种高分辨、低擦地角的地、海杂波，因此已成为重要的杂波建模与仿真的统计模型[1,2]。与瑞利分布等简单模型相比，K分布杂波的建模和仿真较为复杂，而且根据模拟的杂波信号的正交分量和同相分量是否相关，需要分别开展相干和非相干杂波的仿真工作。

为了精确模拟 K分布杂波，国内外诸多学者针对相干和非相干杂波模型进行了一系列深入的研究[3－17]。文献[3]提出了基于球不变随机过程(SIRP)法的相关相干K分布杂波的生成方法。该方法可以模拟复杂波数据，能独立控制杂波的功率谱和幅度分布，但需要求解非线性方程，计算量较大。文献[4]提出了基于零记忆非线性变换(ZMNL)法的相关 K分布杂波的模拟方法。该方法适用于非相干杂波模型，原理简单，主要的缺陷是要求形状参数设置为(半)整数，形状参数(半)整数化会带来杂波模拟偏差，不能独立控制功率谱和幅度分布，为满足功率谱特性需求，相关系数的计算较为复杂。文献[5]证明了 K分布序列的同相正交分量可由两列相互独立的Gaussian矢量加权乘积和构成。基于这一原理，文献[6]和文献[7]提出了新的相关相干K分布杂波建模与仿真方法，与传统SIRP与ZMNL方法相比，新方法可以使生成的杂波具有任意指定的功率谱，而且运算相对简单，易于软件和硬件实现，但对形状参数为非(半)整数的情况仅进行了近似计算处理。文献[10]基于ZMNL方法和线性变换理论提出了一种时空相关相干 K分布杂波的建模方法，减少了杂波模拟的运算复杂度。为了更好地估计杂波背景下雷达恒虚警率检测性能，文献[11]对时间相关相干K分布杂波进行了建模仿真。

本文针对传统ZMNL方法和SIRP方法中存在的部分问题提出改进，主要贡献包括：

(1) 针对传统的非相干模型ZMNL方法中形状参数(半)整数化导致的杂波模拟偏差问题，提出一种增加形状参数非(半)整数部分对应的Gamma分布变量生成支路的改进方法，该方法利用了Gamma分布的第2参数可加性，将杂波的形状参数从(半)整数推广到一般实数，改善了杂波幅度特性模拟性能；

(2) 针对传统的相干模型 SIRP方法中杂波模拟运算量大的问题，给出一种直接产生服从杂波特征分布的调制变量的方法，该方法不需要求解非线性方程，因此极大地提高了杂波模拟效率。

最后，仿真结果验证了本文方法的有效性。

2 传统K分布杂波模拟方法

2.1 K分布杂波模型

K分布的概率密度函数(PDF)为[4]：

其中，a是尺度参数， v是形状参数，Γ(⋅)是Gamma函数，Kv(⋅)是第2类修正Bessel函数。

杂波平均功率δ2,v和a之间的关系可表示为[18]：

杂波的功率谱特性可以用其功率谱密度或自相关函数来表示。常见杂波如地、云雨和箔条杂波的功率谱一般认为服从Gaussian分布，其归一化功率谱表达式为[18]：

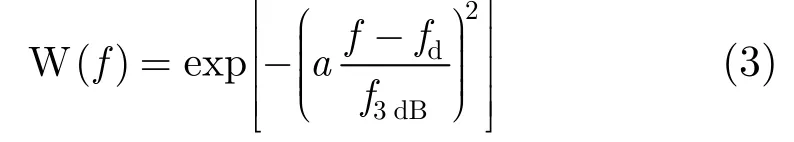
其中，fd是多普勒频率，f3dB是两个半功率点间的带宽。为满足限制条件W(f3dB2)=0.5,a 取值为1.665。

2.2 ZMNL方法

令随机变量 xs～G(xs;2; 1), y ～G(y;2a2;v)，二者相互独立，则z=y xs～K(z ;a; v)[4,19]，其中xs被称为散斑分量，y被称为纹理分量，G(⋅)代表Gamma分布概率密度函数：G(xs;2;1)即为指数分布。

根据前述的通过纹理分量y乘以散斑分量xs获得K分布变量z的思想，传统的基于ZMNL的相关K分布杂波的产生流程如图1所示[4]。框图1中包含两条支路，其中一路利用2v个独立 Gaussian变量的平方和来生成Gamma分布变量，另外一路利用两个独立 Gaussian变量的平方和来产生指数分布变量，两条支路输出的随机变量相乘取平方根得到 K 分布杂波变量。其中，输出序列{zi} (i=1,2,…) 为所需 K分布杂波序列，中间变量{w1,i}, … ,{ w2v+2,i}(i =1,2,…) 均为相关Gaussian随机序列，但是两两之间相互独立。

为了使模拟的杂波不仅在幅度上满足K分布，在功率谱上也满足所需的Gaussian谱特性，通过调整滤波器H1和H2来控制和改变非线性变换后K分布杂波序列的相关系数Sij[4]：

图1 传统相关K分布杂波产生框图Fig. 1 Block diagram for conventional generation of correlated K distributed clutter

其中2F1(α , β; γ; η)为Gaussian超几何分布函数，且Λ=Γ(v+3/2) Γ( 3/2)/Γ(v+1)。rij是 wk(k=1,2,…2v)的相关系数，qij是 wk(k=2v+1,2v+2)的相关系数。该公式具有无限种组合解。实际仿真过程中，可采用傅里叶级数展开法推导出相关系数Sij，再将rij和qij的组合代入式(5)中求解rij和qij，从而计算得到滤波器H1和H2的系数[4,20]。

该方法适用于产生形状参数v为(半)整数的 K分布杂波。若v为非(半)整数，一般可通过向下或向上取(半)整数的方法得到(半)整数v'，此时模拟的杂波满足分布 K(z ; a; v')，它与实际所需分布K(z; a;v)存在一定的偏差。为改善相关K分布杂波幅度特性模拟性能，需要寻求更精确的模拟方法。

2.3 SIRP方法

调制变量序列{si}的平均功率为 1，其平方服从Gamma分布，即～G。最后用{s}调i制复Gaussian变量{yi}即得到相关相干K分布杂波序列{zi}[3,15]。

图 2中，低通滤波器 H1的作用是使{yi}具有{zi}的功率谱形状。低通滤波器H2的作用是使非线性变换后的随机序列的功率谱足够窄，可以采用多阶Butterworth滤波器实现[20]。非线性变换使得{xi}和{si}满足关系[3]：

其中γ(a, b)为低阶不完全Gamma函数，Q(⋅)为标准Gaussian随机变量的尾部面积。化简式(7)到非线性方程：

其中erf(⋅)是误差函数。通过数值方法计算即可根据输入变量序列{xi}得到输出变量序列{si}。

图2 传统相关相干K分布杂波产生框图Fig. 2 Block diagram for conventional generation of correlated coherent K distributed clutter

SIRP方法用符合所要求的单点概率密度函数的随机序列调制相关Gaussian随机过程，能独立控制杂波的功率谱和幅度分布，能够较好地实现对相关相干K分布杂波的模拟。但该法易受序列阶数和自相关函数的限制，而且需要求解非线性方程，计算量较大[17]。

3 改进的K分布杂波模拟方法

3.1 改进的ZMNL方法

那么 y2=2a2ηβ～ G(y2;2a2; v2)[21]。

基于Gamma分布的第2参数可加性，通过在传统产生框图1中添加形状参数的非(半)整数部分对应的Gamma分布变量生成支路，得到改进的相关K分布杂波产生流程如图3所示，其中添加的支路由虚线框出。先将形状参数v分解为(半)整数部分v1和非(半)整数部分 v2。若 v2=0，则按照传统ZMNL方法生成K分布杂波；若v2＞0，则在利用2v1个独立 Gaussian变量经滤波后求平方和得到Gamma分布变量 y1的同时，利用指数分布变量η和 Beta分布变量β生成非(半)整数部分对应的Gamma分布变量y2，从而得到服从分布 G(y;2 a2; v)的变量y。另一支路利用两个独立Gaussian变量经滤波后的平方和生成服从指数分布的变量xs。两路输出的随机变量序列{yi}和{xs,i}相乘后开平方即得到K分布杂波序列{zi}。为使得{y2,i}对输出序列功率谱的影响尽量可以忽略，仍采用式(5)计算推导中间相关系数，本文采用常用组合之一：qij=rij，即令 Gamma分布变量序列{y1,i}和指数分布变量序列{xs,i}的相关系数的权重相等。实际仿真过程中，根据杂波的 Gaussian谱形状推导出相关系数Sij，再将 qij=rij代入式(5)中求解qij和rij，从而计算得到图3中滤波器H1和H2的系数[4,20]。具体实现方法可以采用递推查询法和二分法等，相对而言，二分法算法复杂度较低。

3.2 改进的SIRP方法

对于传统SIRP方法，若能不通过数值方法求解非线性方程而直接产生具有杂波特征 PDF的实非负调制变量s，仿真速度将大大提高。本文在3.1节提出了β为任意正实数时分布G(x; α; β)的生成方法，其运算效率高，而传统SIRP模型中调制变量s的平方服从Gamma分布，所以可以采用图3中生成Gamma分布变量的方法替代传统SIRP方法中求解非线性方程的方法来获得调制变量s，得到改进的相关相干K分布杂波产生流程如图4所示，其中改进的支路由虚线框出。

图4中，标准Gaussian变量序列{w1,i}和{w2,i}所在支路是为了产生复Gaussian变量序列{yi}，其中低通滤波器 H1的作用是使{yi}具有{xi}的功率谱形状。另一支路是为了产生具有杂波特征 PDF的调制变量序列{si}，先利用Gamma分布的第2参数可加性产生服从 Gamma分布的变量序列{pi}，具体实现过程与图3类似，然后开平方得到实非负调制变量序列{si}。特别需要注意的是，图4中低通滤波器H2的作用与图3中H1的作用不同，这里是使调制变量序列{si}的功率谱足够窄，以实现功率谱和幅度分布的独立控制，可以采用多阶Butterworth滤波器实现[20]。

该方法与传统 SIRP 方法相比，产生复Gaussian变量序列的支路相同，而产生调制变量序列的支路不同，该支路不需要通过求解非线性方程来产生具有杂波特征 PDF的实非负调制变量序列{si}，只需要简单的加法、乘法和开平方运算。假设需要产生的K分布序列长度为L，图2和图4中低通滤波器H2的点数均为M。对于传统SIRP方法，产生调制变量序列的支路首先需要进行低通滤波，运算量为O(ML)，然后还需要求解L次非线性方程。若采用二分法求解非线性方程，设定查询区间为 [sl, sh]，误差精度为ε，则每次求解方程需要进行log2((sh-s1)/ε)次积分计算。对于图4所示的改进方法，产生调制变量序列的支路不需要进行积分计算，运算量为 O(v1ML)。文献[22]指出，形状参数v在实际中的取值上限为20，而积分计算的运算量要远大于加法或乘法的运算量，因此当仿真序列长度L较大时，与传统 SIRP方法相比，改进的 SIRP方法能够极大地提升运算速度，提高杂波模拟效率。

图3 改进的相关K分布杂波产生框图Fig. 3 Block diagram for improved generation of correlated K distributed clutter

图4 改进的相关相干K分布杂波产生框图Fig. 4 Block diagram for improved generation of correlated coherent K distributed clutter

4 仿真结果

本文基于 McMaster大学的 IPIX型雷达于1993年在Dartmouth采集的一组典型的高海况下的海杂波数据[23]，利用2阶/4阶矩估计法对数据进行 K分布拟合[24,25]，计算得到形状参数v=2.74，尺度参数a=0.4，根据此组形状参数和尺度参数开展K分布杂波仿真。设定采样频率为 FS=1000 H z ，取采样点数为 N= 5 × 104,K分布杂波功率谱采用Gaussian谱，两个半功率点间的带宽为f3dB= 100 Hz，仿真次数为M=500。

根据图1-图4所示框图进行仿真，图1中形状参数向下取(半)整数即v'=2.5，图2中采用二分法求解非线性方程，设定s1=0,sh=8,ε=10-4，采用 Burg法估计杂波功率谱密度，得到的某次典型仿真结果如图5-图8所示。图5(a)-图8(a)中横坐标为杂波幅度，纵坐标为幅度概率密度，虚线表示K分布杂波的理论幅度概率密度曲线，实线表示仿真得到的杂波序列的幅度概率密度曲线。图 5(b)-图8(b)中横坐标为采样频率，纵坐标为功率谱密度，虚线表示K分布杂波的理论功率谱密度曲线，实线表示仿真得到的杂波序列的功率谱密度曲线。表 1给出了4种方法幅度分布的平均检验统计量和相对运算时间，通过KS检验和 χ2检验来定量比较各种方法的杂波幅度特性模拟性能[26]，通过计算相对运算时间来定量比较各种方法的仿真效率。

图5 传统ZMNL方法Fig. 5 Conventional ZMNL method

图6 传统SIRP方法Fig. 6 Conventional SIRP method

图7 改进的ZMNL方法Fig. 7 Improved ZMNL method

图8 改进的SIRP方法Fig. 8 Improved SIRP method

表1 检验统计量和相对运算时间Tab. 1 Test statistics and relative operation time

观察图5(a)和图7(a)，传统ZMNL方法模拟的杂波的幅度概率密度曲线与理论值有一定的偏差，相比而言，改进的ZMNL方法对相关K分布杂波的模拟效果有明显的改善，这与表 1中改进的ZMNL方法的检验统计量小于传统方法的相符。比较图5(b)和图7(b)发现，忽略图3中变量序列{y2,i}对功率谱的影响，对K分布杂波的功率谱密度带来的影响可以忽略不计。改进的 ZMNL方法与传统ZMNL方法仿真运算所需的时间比为25:26，由此可见，图3所示的改进方法在不增加仿真时间的前提下，改善了K分布杂波的模拟性能。

比较图6(a)和图8(a)，发现改进的SIRP方法对相关相干K分布杂波的模拟效果与传统SIRP方法的效果相当，表1给出的这两种方法的检验统计量也近似相等。比较图6(b)和图8(b)，可知与传统SIRP方法相比，改进的SIRP方法也能获得较理想的功率谱。传统SIRP方法与改进的SIRP方法仿真运算所需的时间比为 112:1。由此可见，图 4所示的改进方法在不影响杂波幅度特性和功率谱特性的基础上，极大地提高了仿真速度。

5 结论

本文对幅度分布特性为K分布、功率谱特性为Gaussian谱的雷达杂波模拟方法进行了研究。针对传统相关K分布杂波模拟方法中形状参数为(半)整数的问题，通过增加Gamma分布生成支路，得到改进的相关K分布杂波的生成方法，将K分布杂波的形状参数从(半)整数推广到一般正实数。针对传统相关相干 K分布杂波模拟方法计算量大的问题，本文给出不通过求解非线性方程直接产生调制变量的改进的相关相干K分布杂波生成方法，运算量大大减小。仿真结果表明，改进的ZMNL方法在不影响仿真时间的基础上，改善了杂波幅度特性模拟的性能；改进的SIRP方法在不影响幅度概率密度分布仿真结果的前提下，有效地提高了仿真速度，节约了仿真时间。

[1] Ward K D. Compound representation of high resolution sea clutter[J]. Electronics Letters, 1981, 17(16): 561-563.

[2] Watts S and Ward K D. Spatial correlation in K-distributed sea clutter[J]. IEE Proceedings F, Communications, Radar and Signal Processing, 1987, 134(6): 526-532.

[3] Conte E, Longo M, and Lops M. Modelling and simulation of non-Rayleigh radar clutter[J]. IEE Proceedings F, Radar and Signal Processing, 1991, 138(2): 121-130.

[4]MarierL J, Jr.. Correlated K-distributed clutter generation for radar detection and track[J]. IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(2): 568-580.

[5]Szajnowski W J. Simulation model of correlated K-distributed clutter[J]. Electronics Letters, 2000, 36(5): 476-477.

[6]杨俊岭, 吕韶昱, 万建伟. 一种新的相干 K 分布模型及其在海杂波仿真中的应用[J]. 系统仿真学报, 2007, 19(2): 250-260.

Yang Jun-ling, Lü Shao-yu, and Wan Jan-wei. A new coherent K-distributed model and its application in sea-clutter simulation[J]. Journal of System Simulation, 2007, 19(2): 250-260.

[7] Huang Dan, Zeng Da-zhi, and Long Teng. A new method for modeling and simulation of coherent correlated K-distributed clutter[C]. 2009 IET International Radar Conference, Guilin, 2009: 1-5.

[8] Davidson G. Simulation of coherent sea clutter[J]. IET Radar, Sonar & Navigation, 2010, 4(2): 168-177.

[9] Roy L P and Kumar R V R. Accurate K-distributed clutter model for scanning radar application[J]. IET Radar, Sonar & Navigation, 2010, 4(2): 158-167.

[10]Teng L, Dan H, and Di Y. Model for spatial-correlated clutter and its application to temporal-spatial correlated clutter[J]. IET Microwaves, Antennas & Propagation, 2011, 5(3): 298-304.

[11]Yang Yong, Xiao Shun-ping, Feng De-jun, et al.. Modelling and simulation of spatial-temporal correlated K distributed clutter for coherent radarseeker[J]. IET Radar, Sonar & Navigation, 2014, 8(1): 1-8.

[12]宋新, 张长隆, 周良柱. ZMNL方法实现海杂波建模与仿真[J].现代雷达, 2003, 25(3): 24-35.

Song Xin, Zhang Chang-long, and Zhou Liang-zhu. Modeling and simulation of coherent and nocoherent correlation radar sea clutter using ZMNL[J]. Modern Radar, 2003, 25(3): 24-35.

[13]宋海娜, 胡卫东, 郁文贤, 等. 低入射余角下雷达海杂波的建模与仿真[J]. 国防科技大学学报, 2000, 22(3): 29-33.

Song Hai-na, Hu Wei-dong, Yu Wen-xian, et al.. Modeling and simulation of low grazing angle radar sea clutter[J]. Journal of National University of Defense Technology, 2000, 22(3): 29-33.

[14]杜勇, 李依林, 杨海粟, 等. 基于 ZMNL法的相关雷达杂波建模与仿真[J]. 火控雷达技术, 2012, 41(4): 11-14.

Du Yong, Li Yi-lin, Yang Hai-su, et al.. Modeling and simulation of ZMNL-based correlated radar clutter[J]. Fire Control Radar Technology, 2012, 41(4): 11-14.

[15]王岩松. 海杂波建模与仿真技术研究[D]. [硕士论文], 国防科学技术大学, 2003.

Wang Yan-song. Modeling and simulation of radar sea clutter[D]. [Master dissertation], National University of Defense Technology, 2003.

[16]陈志刚. SIRP法相干K分布雷达海杂波建模与仿真[J]. 中国科技财富, 2009, (8): 93-95.

Chen Zhi-gang. Modeling and simulation of coherent K-distributed sea clutter using SIRP[J]. Fortune World, 2009, (8): 93-95.

[17]刘明园, 邓有为, 何建军, 等. SIRP法相干相关K分布雷达杂波仿真[J]. 战术导弹技术, 2011, (4): 98-101.

Liu Ming-yuan, Deng You-wei, He Jian-jun, et al.. Simulation of coherent correlation K-distributed radar clutter based on SIRP[J]. Tactical Missile Technology, 2011, (4): 98-101.

[18]陈金明. 雷达杂波建模与仿真[D]. [硕士论文], 西安电子科技大学, 2010.

Chen Jin-ming. Modeling and simulation of radar clutter[D]. [Master dissertation], Xidian University, 2010.

[19]Watts S. Radar detection prediction in sea clutter using the compound K-distribution model[J]. IEE Proceedings F, Communicatoins, Radar and Signal Processing, 1985, 132(7): 613-620.

[20]罗军辉, 罗勇江, 白义臣, 等. MATLAB 7.0 在数字信号处理中的应用[M]. 北京: 机械工业出版社, 2005: 180-184.

Luo Jun-hui, Luo Yong-jiang, Bai Yi-chen, et al.. MATLAB 7.0 in the Application of Digital Signal Processing[M]. Beijing: China Machine Press, 2005: 180-184.

[21]Reuven Y. Rubinstein. Simulation and the Monte Carlo Method[M]. Canada: John Wiley & Sons, 1981: 71-80.

[22]Irina Antipov. Analysis of sea clutter data[R]. 1998.

[23]McMaster University. IPIX radar database[OL]. http://soma. ece.mcmaster.ca/ipix/dartmouth/datasets.html, 1998.

[24]Iskander D R and Zoubir A M. Estimation of the parameters of the K-distribution using higher order and fractional moments[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(4): 1453-1457.

[25]杨海文. 海杂波建模与实测数据分析[D]. [硕士论文], 西安电子科技大学, 2011.

Yang Hai-wen. Modeling and data analysis of sea clutter [D]. [Master dissertation], Xidian University, 2011.

[26]Anastassopoulos V and Lampropoulos G A. High resolution radar clutter statistics[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(1): 43-60.

朱洁丽(1989-)，女，安徽安庆人，清华大学硕士研究生，研究方向为雷达信号处理。

E-mail: smile_zjl@163.com

汤 俊(1973-)，男，江苏南京人，清华大学副教授，博士生导师，主要研究方向为MIMO雷达、信息论、阵列信号处理、通用高速实时信号处理系统。

K-distribution Clutter Simulation Methods Based on Improved ZMNL and SIRP

Zhu Jie-li Tang Jun
(Department of Electronic Engineering, Tsinghua University, Beijing 100084, China)

Zero Memory NonLinearity (ZMNL) and Spherically Invariant Random Process (SIRP) are two commonly used methods in K-distribution clutter simulations. An improved simulation method, which adds abranch of Gamma-distributed variable and extends the shape parameter to arbitrary positive real, is proposed to address the clutter simulation error in the conventional ZMNL method. To reduce the computation required for the conventional SIRP method, an improved method of modulation variable generation is also proposed, what avoids large computations for solving nonlinear equations and improves the simulation speed. The simulation results verify the effectiveness of the improved methods.

K distribution; Radar clutter; Correlation; Coherent

TN957

A

2095-283X(2014)05-0533-08

10.3724/SP.J.1300.2014.13124

2013-12-12收到，2014-03-20改回；2014-05-26网络优先出版

61171120)，清华大学自主科研基金 (20131089362)，国家部委重点基金(9140A07020212JW0101)资助课题

*通信作者： 朱洁丽 zhu-jl10@mails.tsinghua.edu.cn