基于分组格雷编码的OFDM雷达通信一体化系统峰均功率比抑制

李自琦 梅进杰 胡登鹏 沈序驰 李晓柏

(空军预警学院 武汉 430019)

基于分组格雷编码的OFDM雷达通信一体化系统峰均功率比抑制

李自琦*梅进杰 胡登鹏 沈序驰 李晓柏

(空军预警学院 武汉 430019)

基于OFDM共享信号的雷达通信一体化系统具有较高的峰均功率比，由于编码率的限制，采用格雷序列编码抑制系统峰均功率比(PAPR)的算法只适合应用于子载波数较少的场合。针对子载波数较多的系统，该文提出一种利用分组并行格雷编码结合系数加权优化的PAPR抑制算法，通过将输入比特流分为若干组并行比特，分别进行格雷序列编码、数据符号调制以及逆傅里叶变换，将结果合并就可以得到一个OFDM符号。在合并之前对每一组引入若干加权系数，这样就构成了多个可供选择的OFDM符号，通过选择具有最小PAPR值的OFDM符号作为发射信号，实现系统PAPR抑制。最后，仿真了3种不同分组方案下PAPR抑制能力、通信误码率以及雷达宽带模糊函数，仿真结果表明，该算法可有效抑制系统 PAPR，降低系统误码率，其雷达宽带模糊函数仍为近似图钉型，具有良好的距离和速度分辨能力以及测距、测速精度。

正交频分复用(OFDM)；雷达通信一体化；峰均功率比(PAPR)；格雷互补码；宽带模糊函数

1 引言

将多种电子设备综合一体化成为未来军用电子系统发展的趋势之一[1]。雷达通信一体化是多功能电子系统综合一体化的重要内容。将雷达通信一体化系统应用于作战平台，不仅可以节省作战平台的空间(尤其是空中、空间和舰艇平台)，增强其机动性，而且能够减少设备间的电磁干扰，提高其作战效能。基于OFDM共享信号的一体化系统[2－5]具有较高的分辨率以及低截获概率的优点，同时具有较高的传输速率，较高的频谱利用率，优良的抗干扰能力，成为近年来学者研究的重点。然而OFDM系统存在峰均功率比(Peak-to-Average Power Ratio, PAPR)较高的缺点，高PAPR信号通过高功率放大器(High Power Amplifier, HPA)时，不仅会导致放大器效率降低，而且会导致信号失真，频谱扩展，系统性能下降，因此必须在一体化系统发射端对PAPR进行抑制。

目前针对多载波相位编码雷达(MCPC)和OFDM 通信中的高峰均功率比问题，学者们提出了多种方案，由于雷达与通信功能的不同，二者在抑制峰均功率比时考虑的重点也不同，对峰均功率比的要求也不同。通信主要考虑的是传输信道的容量、速率以及如何确保信号在传输过程中不失真，通信信号处理的主要是为了获取调制方式及所携带的信息，因此PAPR抑制时主要考虑信号是否发生失真，以及PAPR抑制算法对传输速率和信道容量带来的影响[6]；雷达主要考虑的是在有限的发射功率条件下，如何更远、更快地发现目标，以及如何从目标回波中提取更多、更准确的目标信息，一般不考虑波形失真，在尽量降低信号的峰均功率比的同时考虑其模糊函数性能以及自相关函数性能[7]。针对雷达通信一体化系统，不能简单地应用多载波相位编码雷达(MCPC)或OFDM通信中的PAPR抑制算法，PAPR在满足一体化系统要求的条件下，还要考虑系统的传信率、误码率性能以及目标检测性能。目前针对OFDM雷达通信一体化系统的高PARP问题研究较少，文献[8]提出将OFDM符号再进行调频或调相，产生的信号包络恒定(CE-OFDM)，其PAPR可为0 dB，但以牺牲频谱效率为代价，同时存在小信噪比时的门限效应不利于在小信噪比下通信数据的解调。

在MCPC和OFDM通信中都可以利用编码法降低系统峰均功率比，但是二者在应用中略有不同：在MCPC中将具有理想周期自相关性能的序列循环移位后构成互补集合[9]或者直接构造互补序列[10]，而通信中是将随机的通信信息编码为格雷序列，二者降低峰均功率比的原理是一样的。因此考虑采用格雷编码来抑制一体化系统 PAPR。文献[11]利用格雷序列与RM码的关系，将输入比特编码为格雷序列，可以使系统PAPR不大于3 dB，而且具有RM码良好的检错/纠错能力。由于编码长度越长，编码率越低，因此该算法不宜直接用于子载波数较大的系统。针对子载波数较大的场合，本文提出了一种分组并行格雷编码的PAPR抑制算法，给出了相应的实现框图，最后对3种分组方案下不同编码率的分组编码进行了计算机仿真和性能分析。

2 信号模型

其中N为OFDM系统子载波数，Δ f =1/T 为子载波间隔，T为脉冲宽度，xn为第n个子载波上经过基带调制后的调制符号，fc为载波频率。

由于峰均功率比是一个随机变量，因此需要从统计角度对其进行分析，即计算峰均功率比超过某

基于 OFDM共享信号的雷达通信一体化系统结构如图1所示，通信数据经过调制成一体化共享信号，经过天线发射出去，接收机通过对接收到的目标回波和合作目标发射的一体化信号进行处理，该系统可以同时完成目标探测和通信信息传输的功能。

假设雷达通信一体化系统为脉冲工作方式，一个脉冲内只发射一个OFDM符号，发射信号复包络可以表示为：一门限值 PAPR0的概率，常用互补累积分布函数(CCDF)来描述信号的峰均功率比：

图1 雷达通信一体化系统框图Fig. 1 Block diagram of integrated radar and communication system

在随后的讨论中，采用CCDF来衡量OFDM系统内的PAPR分布。

3 PAPR抑制算法

可以证明，如果系统发射的信号是一组互补序列，则系统PAPR不大于3 dB。Davis等人[11]率先发现了RM码与格雷序列的关系，成功地进行了格雷序列编码，并提出了高效的译码算法。通过将输入信息比特编码为格雷序列后，不仅可以使系统PAPR不大于3 dB，还使码字具有较强的纠错/检错能力，能够较好地改善系统性能。本文基于格雷序列编码原理[11]，提出了一种可应用于子载波较多系统的PAPR抑制算法，通过仿真分析了其有效性。

3.1 格雷序列编码原理

RM码最先由Muller于1954年最先提出，同年，Reed用大数逻辑译码解决了它的译码。RM码最早是从线性空间的角度出发构造的，以后发现它与循环码、几何码和格等有密切关系，因此这是很重要的一类线性码。文献[11]利用2阶RM码中1阶RM码的陪集，将信息比特编码为格雷序列，后来被学者进一步推广到了一般情况[12]。

有限域Z2h,h ≥ 1上长度为2m的二进制r阶RM码记作RM2h(r, m)，有限域Z2h,h ≥ 1上长度为2m的多进制r阶RM码记作 ZRM2h(r, m)，二者都可由生成矩阵定义，生成矩阵见文献[13]。根据文献[11]，具体的编码步骤主要分3步：

第 1步 根据RM2h(r, m)码的生成矩阵，构建陪集首表，根据输入信息的前w比特选择相应的陪集首，其中可用来将信息比特编码为格雷序列的陪集首共有m!/2个，为了方便应用只用其中 w个，其中：

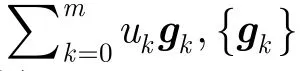
2h矩阵的各行向量。

第3步 将第1步和第2步的结果相加(模2h)，就可以得到一个码字。

通过编码过程可以看出，每次将 w+h(m+1)位二进制信息比特通过格雷序列编码为长度为2m的2h进制码字，定义编码效率R：

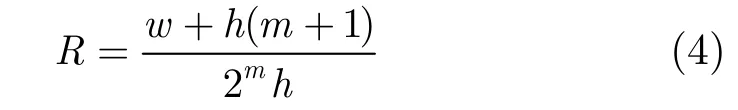
由图2中可以看出，w, h对编码效率的影响较小，m对编码效率影响较大，随着编码长度的增加，编码效率急剧下降，因此实际应用该算法进行编码时编码长度不宜过长，也就是说，不能用于子载波较多的场合，一般认为仅可用于子载波数小于32的OFDM系统。

图2 不同h和m取值下编码率仿真Fig. 2 Coding rate under different h and m

3.2 分组格雷序列编码的PAPR抑制算法

采用格雷序列来降低系统 PAPR，其码字长度不能过长，不宜直接用于子载波数较多的系统，借鉴PTS算法，本文针对子载波较多的系统，提出了一种分组并行编译码抑制PAPR的算法，其基本框图如图3所示。

若系统子载波数为 N，用向量a= {a0, a1, ⋅⋅⋅,ak-1}定义输入信息比特流，然后把a分为L组，分别由{al,l=1,2,⋅⋅⋅,L}来表示，将每一组进行格雷序列编码成长度为2m的码字，这样就产生了L组码字，对L组码字分别进行MPSK调制得到数据符号{Xl,l=1,2,… , L}，然后对其进行N点的逆傅里叶变换(IFFT)为{xl,l=1,2,⋅⋅⋅,L}，再将输出结果进行组合即可得到一个OFDM符号。显然，输入比特数k是与编码率有关的常数。

图3 所提算法结构框图Fig. 3 Block scheme of the proposed algorithm architecture

通过格雷序列编码后，第l组的PAPR不大于3 dB，但是将L组符号相加后，由于相位的随机性，其PAPR仍然可能较大，因此对L组符号引入加权系数：{bl, l=1,2,⋅⋅⋅,L }，满足 bl=exp(j ϕl)，以及ϕl∈ [0,2π]。bl表示第l组数据符号加权系数。通过系数最优化，最后选择具有最小PAPR值的信号作为输出信号。

综上所述，一个OFDM符号可以表示为：

其中argmin(⋅)表示函数取得最小值时使用的判决条件。

由图2可以看出，采用本算法进行分组并行格雷序列编码后，可以在子载波数较大的情况下不致于恶化编码率，对各分组引入加权系数后，通过系数寻优进一步降低PAPR，本算法的PAPR性能与单独采种 PTS算法时相当，但本算法的优势在于具有RM码较好的检错/纠错能力。本算法的计算复杂度主要集中在格雷序列编码、逆傅里叶变换以及加权系数寻优的过程中。完成每一组格雷序列编码需要进行(m+1)次乘法和1次加法，由于乘法和加法都是模2h运算，实际实现时并不会大幅增加系统开销；而L组并行的傅里叶变换较原系统并没有增加复杂度，在接收端可以采用相似的并行结构以进行解调，有利于提高处理速度；求1次PAPR需要作N点复数乘法和N次实数加法，由于1次复数乘法需要作4次实数乘法和2次实数加法，假设bl包括P个相位值，则总共需要PL次PAPR的比较，故完成一次寻优需计算4 NPL次实数乘法和3NPL次实数加法；因此本算法较原系统增加的计算量为 L(m+1)次模2h乘法和L次模2h加法，4 NPL次实数乘法、3N PL次实数加法。

4 性能仿真结果

若系统子载波数N=128，每个脉冲只发射一个OFDM符号，脉冲宽度码元长度T=0.2 μ s ，子载波间隔δf=1/T=5 MHz，则系统带宽为B=NΔf= 640 MHz。循环前缀长度 tcp=0.025μ s ，载波频率为10 GHz，采用QPSK调制样式，也即h=2。

显然，在子载波数一定的情况下不同的分组数导致不同的编码长度，因此具有不同的编码率，将信号合并后也具有不同的PAPR性能。考虑3种分组方案，将输入信息比特分为16组，8组，4组，也即L分别为16, 8, 4，格雷序列编码长度分别为8, 16, 32，在编码时每一种方案采用3种陪集首数，如表1所示。

在仿真时，按PAPR从小到大的顺序将所有陪集首排序，依次从中选择相应数目的陪集首。在ZRM2h(2,m)码中包含RM2h(1,m)码的m!/2个陪集首，可用于将信息比特编码为格雷序列，对于3种分组方案，可用于将信息比特编码为格雷序列的陪集首数分别为3, 12, 60，使用陪集首个数越多，编码率越大，但是当使用的陪集首数目大于上述3个值时，编码后的序列不再为格雷序列，其PAPR也相应较大。由于普通的RM码并无抑制PAPR能力，为了进行对比，本文在编码时只引入了较少的非格雷序列编码陪集首，3种方案中非格雷序列编码陪集首占可用陪集首的比例分别为1/4, 1/4, 1/16，方案2中陪集首见文献[9]表Ⅲ，方案1和方案3中非格雷序列编码陪集首如表2，表3所示。

表1 3种分组方案Tab. 1 The three block schemes

表2 方案1非格雷序列编码陪集首Tab. 2 The none Golay coding coset representative of No. 1 scheme

表3 方案3非格雷序列编码陪集首Tab. 3 The none Golay coding coset representative of No. 3 scheme

4.1 PAPR抑制性能

为了验证本算法的有效性，对原信号、只进行分组格雷序列编码以及本文算法抑制PAPR性能进行了仿真，为了使离散时间OFDM信号的PAPR性能即可接近于连续时间OFDM信号的PAPR性能，对信号进行了4倍过采样，共仿真105次。

图4，图5，图6为3种分组方案不同编码率下的PAPR抑制性能的仿真结果，从中可以看出，只进行分组格雷序列编码后能够在一定程度上抑制系统PAPR，分组数目越少，PAPR抑制性越好，应用本文算法对每一分组进行加权，PAPR抑制性能更加明显。从图中还可以看出，每种分组方案中采用不同编码率时对PAPR性能影响不是很大，由表1可以看出，虽然在采用非格雷序列编码时，各分组的最大PAPR分别为6.0 dB, 6.0 dB, 5.2 dB，由于N个信号相位的随机性以及非格雷序列码字在整个码字中所占比例较小，合成后的信号PAPR并没有大幅增加。

显然，方案1中可用陪集首数为4时，编码率最大；方案2，方案3可用陪集首数为8, 32时，PAPR抑制性能略优，且编码率适中。图7对3种分组方案下PAPR抑制性能进行了对比，仿真中方案1，方案2，方案3可用陪集首分别为4, 8, 32，由图中可以看出，应用本算法后，3种分组方案抑制PAPR性能基本相当，方案2 PAPR抑制性能略优，PAPR大于7 dB的概率约为 10-4，而原信号PAPR大于7 dB的概率为1。

图4 方案1不同编码率下PAPR抑制性能Fig. 4 PAPR performance of No. 1 scheme with different coding rates

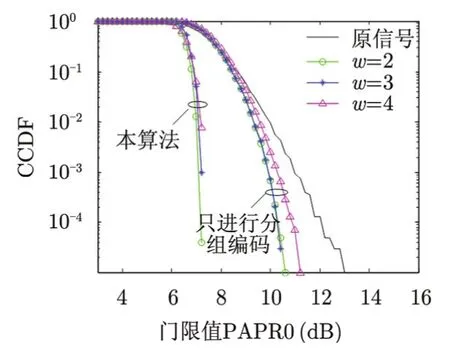
图5 方案2不同编码率下PAPR抑制性能 Fig. 5 PAPR performance of No. 2 scheme with different coding rates

图6 方案3不同编码率下PAPR抑制性能Fig. 6 PAPR performance of No. 3 scheme with different coding rates

4.2 误码率性能

通过编码过程可以看出，所有的许用码字集合实质上是2阶RM码的一个子集，因此，将输入信息比特编码为格雷序列后，不仅可以有效抑制系统PAPR，而且还具有RM码良好的检错/纠错能力，采用本算法构造的码字最小汉明距离不仅与编码长度有关，还与所用陪集首有关，因此本文对采用 3种分组编码方案在AWGN信道和Rayleigh衰落信道下的误码率进行了仿真，采用文献[11]中硬判决译码，仿真中方案1，方案2，方案3可用陪集首数分别为4, 8, 32。Rayleigh信道为2径衰落信道，2径信道的时延分别为0, 0.01 μs，并且第2径平均功率比第1径平均功率低3 dB。

图7 3种分组方案PAPR抑制性能对比Fig. 7 PAPR performance comparison of three block schemes

图8为3种分组方案系统误码率的仿真结果，由图中可以看出，在误码率为 10-3时，采用方案 3分组时编码增益最大(AWGN信道约为 6 dB, Rayleigh信道约为9 dB)，其次是方案2(AWGN信道约为 4 dB, Rayleigh信道约为 5 dB)和方案 1 (AWGN信道和Rayleigh信道都约为1 dB)，显然，在子载波数一定的情况下，分线数目越多，发射端和接收端需要的并行处理通道也越多，可以提高处理速度，同时每一组编码长度较小，可以获得较高的编码率，但是编码增益就越小，分组数较少时反之。由表1可以看出，采用方案3时编码效率最低，显然，误码率性能的提高是通过编码率的降低来获得的。由图8中可以看出，在AWGN信道，采用方案2和方案3分组编码时，在输入信噪比大于6 dB时误码率已经为0，对于一体化系统是非常有益的。在实际应用中可以根据系统传信率和误码率指标灵活选择分组方案。

4.3 宽带模糊函数

模糊函数是通过一个函数表达式定量地描述一种发射信号波形在一个系统中对不同距离、不同速度目标的分辨能力，常用的模糊函数为WoodWard窄带模糊函数，但OFDM信号为一种宽带信号，利用WoodWard窄带模糊函数时有一定的局限性，本文采用文献[14]的宽带模糊函数：

其中γ=1+β为拉伸因子，β= 2ν/c 为多普勒扩展因子，‘*’表示复数共轭。

本文对采用本文算法进行PAPR抑制的系统宽带模糊函数进行了仿真，如图9所示，由归一化模糊函数图可以看出，采用本文算法对系统PAPR进行抑制后，其宽带模糊函数仍为近似的图钉形，具有良好的距离和速度分辨能力以及测距、测速精度。

5 结论

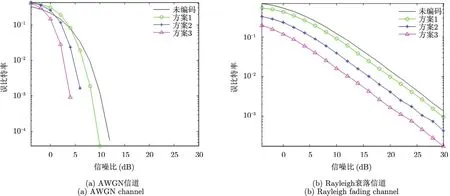
图8 3种分组方案系统误码率仿真Fig. 8 System BER performance of three block schemes

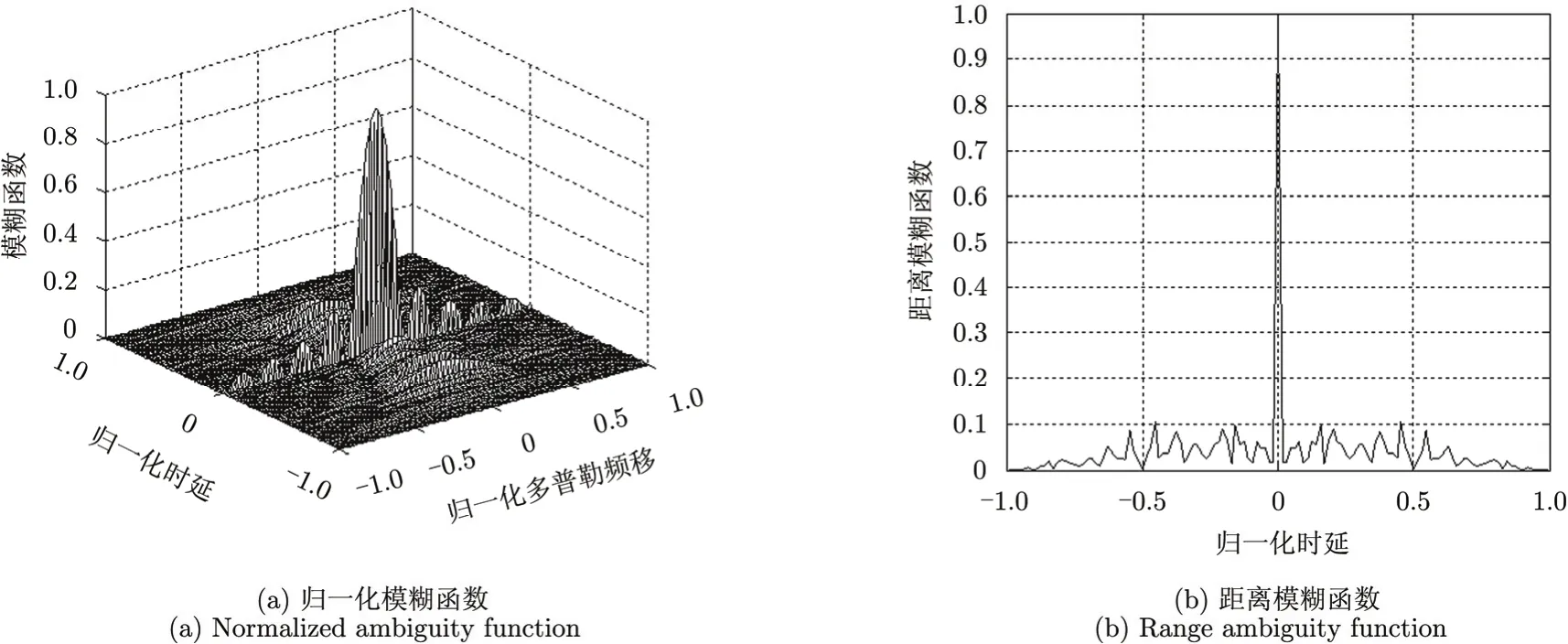
图9 系统宽带模糊函数Fig. 9 The wideband ambiguity function

本文研究了通过格雷互补序列编码抑制雷达通信一体化系统PAPR的算法，由于不适合直接应用于子载波数较多的场合，本文针对子载波数较多的系统，提出了一种分组并行编码结合系数加权优化抑制PAPR的算法，不同分组方案以及不同的编码率下仿真表明，该算法不仅能够有效抑制系统PAPR，且具有良好的检错/纠错能力，在信噪比较低时就可以实现可靠通信，实际应用中可根据系统传信率和误码率指标进行分组编码；同时本文对采用本文算法的一体化系统宽带模糊函数进行了仿真，结果表明，利用本文算法后系统宽带模糊函数仍然为近似图钉形，具有良好的距离和速度分辨能力以及测距、测速精度。

[1]张明友. 雷达-电子战-通信一体化概论[M]. 北京: 国防工业出版社, 2010: 1-25.

Zhang Ming-you. The Conspectus of Integrated Radar, Electronic Warfare and Communication[M]. Beijing: National Defense Industry Press, 2010: 1-25.

[2] Genderen P van. A communication waveform for radar[C]. International Conference on Communication (COMM), Bucharest, Romania, 2010: 289-292.

[3] Garmatyuk D, Schuerger J, and Kauffman K. Multifunctional software-defined radar sensor and data communication system[J]. IEEE Sensors Journal, 2011, 11(1): 99-106.

[4]Sturm C and Wiesbeck W. Waveform design and signal processing aspects for fusion of wireless communications and radar sensing[J]. Proceedings of the IEEE, 2011, 99(7): 1236-1259.

[5]李晓柏, 杨瑞娟, 程伟. 基于Chirp信号的雷达通信一体化研究[J]. 雷达科学与技术, 2012, 10(2): 180-186.

Li Xiao-bai, Yang Rui-juan, and Cheng Wei. Integrated radar and communication based on Chirp[J]. Radar Science and Technology, 2012, 10(2): 180-186.

[6] Zhang Shun, Ge Jian-hua, Hou Jun, et al.. Partial transmit sequence using EVM optimization metric for BER reduction in OFDM systems[C]. International Conference on Communications and Networking in China (CHINACOM), Guilin, China, 2013: 113-117.

[7]邓斌, 魏玺章, 黎湘. 基于编码序列随机移位的 MCPC雷达信号设计方法研究[J]. 国防科学技术大学学报, 2011, 33(2): 68-72.

Deng Bin, Wei Xi-zhang, and Li Xiang. Parameter designing of random shifted phase-coded MCPC radar signal[J]. Journal of National University of Defense Technology, 2011, 33(2): 68-72.

[8]Thompson S C and Stralka J P. Constant envelope OFDM for power-efficient radar and data communications[C]. International Waveform Diversity and Design Conference, Kissimmee FL, USA, 2009: 291-295.

[9]Mozeson E and Levanon N. Multicarrier radar signals with low peak-to-mean envelope power ratio[J]. IEE Proceedings Radar, Sonar and Navigation, 2003, 150(2): 71-77.

[10]Garcia E, Urena J, Garcia J, et al.. Genetic algorithm for searching a doppler resilient multilevel complementary waveform[C]. IEEE International Symposiumon Intelligent Signal Processing (WISP), Floriana, Malta, 2011: 1-5.

[11]Davis J A and Jonathan J. Peak-to-mean power control in OFDM, Golay complementary sequences, and Reed-Muller codes[J]. IEEE Transactions on Information Theory, 1999, 45(7): 2397-2417.

[12]Chao Y C, Chung H W, and Chi C C. Complementary sets and Reed-Muller codes for peak-to-average power ratio reduction in OFDM[J]. IEEE Communications Letters, 2008, 12(11): 849-851.

[13]Bai G, Zhong Z, Xu R, et al.. Golay complementary sequences and Reed-Muller codes based PAPR reduction for relay networks with superimposed training[C]. IEEE International Conference on Signal Processing (ICSP), Beijing, 2012: 1558-1561.

[14]Sen S and Nehorai A. Adaptive design of OFDM radar signal with improved wideband ambiguity function[J]. IEEE Transactions on Signal Processing, 2010, 58(2): 928-933.

李自琦(1987-)，男，甘肃张掖人，94005部队助理工程师，现为空军预警学院信息与通信工程专业硕士研究生，主要研究方向为现代通信技术、雷达通信一体化。

E-mail: liziqiglee@126.com

梅进杰(1970-)，男，湖北随州人，2003年毕业于华中科技大学光电子工程系，并获博士学位，空军预警学院副教授，研究生导师，主要研究方向为雷达组网通信、光通信系统和光收发模块。

E-mail: meijinjie@tom.cn

胡登鹏(1982-)，男，四川德阳人，2010年毕业于国防科学技术大学信息与通信工程专业，并获博士学位，空军预警学院讲师，主要研究方向为军用无线通信与侦察、数字信号处理、雷达通信一体化。

E-mail: hudengpeng@163.com

沈序驰(1991-)，男，湖北武汉人，空军预警学院信息与通信工程专业硕士研究生，主要研究方向为现代通信技术。

E-mail: 1196533437@qq.com

李晓柏(1983-)，男，甘肃陇西人，2013毕业于空军预警学院信息与通信工程专业，并获博士学位，主要研究方向为现代通信技术、雷达通信一体化。

E-mail: lxb2cici@163.com

Peak-to-Average Power Ratio Reduction for Integration of Radar and Communication Systems Based on OFDM Signals with Block Golay Coding

Li Zi-qi Mei Jin-jie Hu Deng-peng Shen Xu-chi Li Xiao-bai
(Air Force Early Warning Academy, Wuhan 430019, China)

Integration of radar and communication systems based on OFDM signals results in large Peak-to-Average Power Ratio (PAPR). Limited by the code rate, algorithm that use the Golay sequence code to restrain PAPR can only be applied under the condition of a few subcarriers. This study proposes an algorithm to restrain the PAPR of systems with a large number of subcarriers. The algorithm combines the group parallel code with the optimization of weight coefficients. First, bit streams are divided into several groups of parallel bits. Next, every group proceeds with Golay sequence coding, data symbol modulating and inverse Fourier transform. Finally, the parallel result is combined with an OFDM symbol. Before the parallel data are combined, several weight coefficients for every group are introduced; thus, the system has several candidate symbols for transmitting. Then the symbol with minimum PAPR is then selected as the transmitting signal, and the PAPR of the whole system is reduced. PAPR performance, Bit Error Radio (BER) and wideband ambiguity function of three block methods with different coding rate are also simulated. The simulations show that the PAPR of the system decreases and the BER performance improves significantly. The signal exhibits a thumbtack ambiguity function, which suggests good resolution and accuracy for distance and velocity measurements.

Orthogonal Frequency Division Multiplexing (OFDM); Integration of radar and communication; Peak-to-Average Power Ratio (PAPR); Golay complementary sequence; Wideband ambiguity function

TN957

A

2095-283X(2014)05-0548-08

10.3724/SP.J.1300.2014.14059

2014-03-27收到，2014-08-25改回；2014-09-19网络优先出版国家自然科学基金项目(61271451)资助课题

*通信作者： 李自琦 liziqiglee@126.com