基于张量分解的多维数据填充算法

朱彦君，吴向阳

(杭州电子科技大学计算机学院，杭州 3 10018)

基于张量分解的多维数据填充算法

朱彦君，吴向阳

(杭州电子科技大学计算机学院，杭州 3 10018)

在多维数据分析和处理中，经常会出现部分数据丢失或者部分数据未知的情况，如何利用已知数据的潜在结构对这些缺失数据进行填充是一个亟待解决的问题。目前对于缺失数据填充的研究大多是针对矩阵或者向量形式的低维数据，而对于三维以上高维数据填充的研究则很少。针对该问题，提出一种基于张量分解的多维数据填充算法，利用张量分解中CP分解模型的结构特性和分解的唯一性，实现对多维数据中缺失数据的有效填充。通过实验对以三维形式存储的部分数据缺失图像进行填充修复，并与CP-WOPT算法进行比较，结果表明，该算法具有较高的准确度以及较快的运行速度。

缺失数据填充；张量分解；多维数据填充；多维数据分析；多维数据处理；图像修复

1 概述

在生物信号处理、化学数据分析、数据挖掘、机器学习等方面，经常需要处理部分数据缺失的多维数据[1]。这些缺失的数据可能是因为丢失或者无法观察到而引起的，是不可避免的。现阶段大部分处理数据的算法都是基于完整的数据。例如在数据挖掘中，对含有缺失数据的多维数据进行分析，有可能建立错误的挖掘模型。处理缺失数据的方法大致分为3类：删除元组，数据填充和不处理[2]。目前，最有效地分析和处理这些多维数据的方法，就是给缺失数据一个填充值[3-4]。过去，数据填充局限于二维矩阵或者向量形式的低维数据[5-6]，对于高维数据填充的研究很少。Acar E等人于2011年提出了CP-WOPT算法[7]，可以对高维数据进行填充，但它是基于梯度值最优的方法对缺失数据进行估计的，因此，填充数据非常不准确。

本文提出一种基于张量分解[8]的多维数据填充算法，称为CPWF(Candecomp/Parafac Weighted Filling)算法。它可对高维数据进行填充，并且能够充分挖掘所有已知数据的潜在结构[9]，实现对缺失数据的准确填充。为了便于观察和描述，实验中将彩色图像按三维形式存储并进行处理，但该算法不局限于三维数据，任意维数据均可处理。

2 预备知识

2.1 张量的矩阵化

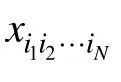
由于张量矩阵化的形式不唯一，不同的矩阵化方法会导致完全不同的计算结果，因此本文中的矩阵化方法如无特殊说明，均指本节所说的矩阵化方法。

为了便于理解，这里用一个实例作为说明。假设有一个张量X(3× 4×2)：

2.2 C P分解模型

一个张量可看成一个多维数组。张量特别是高维的张量，在应用上实现对数据和实际情况较为准确的建模，但是这种建模方法使得张量的计算成为一个巨大问题。因此，需要对张量进行分解，以降低其维数，减少计算的复杂度，并能够最大程度保留原始数据的特征。现有的张量分解法主要有CP分解法和Tucker分解法。本文只关注CP分解法。

为了便于理解，本文以一个三维张量X(I×J×K)为例，高于三维的情况可以很容易的推导出来。X的CP分解模型如图1所示。

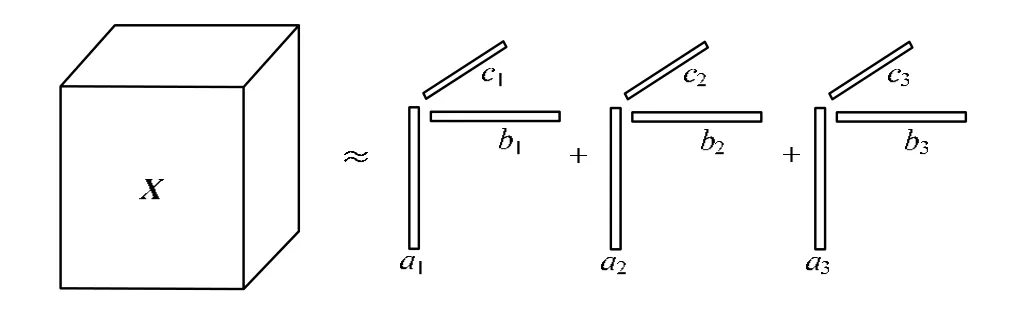
图1 三维张量的CP分解模型

张量的元素值与分解后的向量元素值之间的关系如下：

如果将矩阵A(I×R)看成由a1～aR共R个列向量构成的矩阵，将矩阵B(J×R)看成由b1～bR共R个列向量构成的矩阵，将矩阵C(K×R)看成由c1～cR共R个列向量构成的矩阵，那么X、A、B、C之间有如下性质：

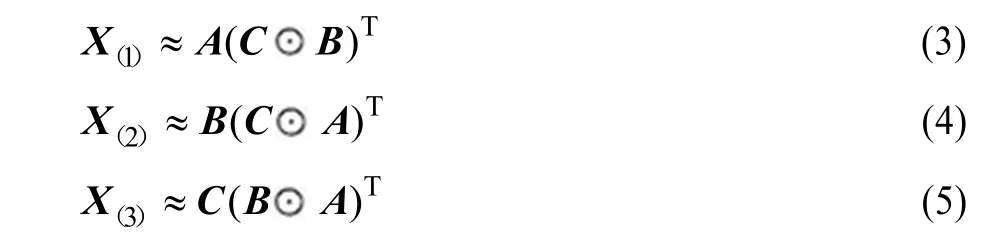
其中，X(n)表示张量X的第n维矩阵化[8]；表示Khatri-Rao积[10]；T表示矩阵的转置。

CP分解的目的是求出A，B，C这3个矩阵。假设R值是给定的，那么问题转化为：

其中，“*”表示矩阵的Hadamard积[8]。

由于CP分解是唯一的[11]，因此迭代一定会收敛。当R大于张量的秩[12]时，

3 CP-WOPT算法简介

CP-WOPT算法[7]可以对高维数据进行填充。

给定一个部分数据缺失的张量X，定义一个记录缺失信息的权值张量W如下：

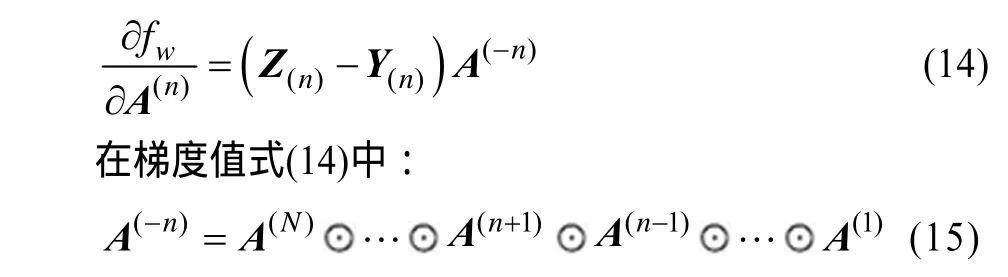
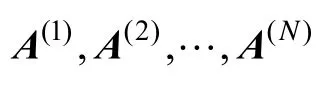
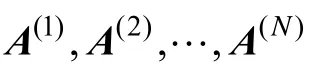
4 CPWF算法

4.1 算法步骤

本文提出算法称为CPWF算法。为了便于理解，以三维张量为例，高于三维的情况可以很容易推导出来。

为了记录哪些数据丢失，定义一个和原始张量大小相同的权值张量W如下：

该文提出的CPWF算法具体如下：

(1)给定张量X和记录缺失数据位置的张量W；

(2)随便填充张量X的缺失数据(随机数或者平均值)；

(3)初始化A，B，C和R；

4.2 算法原理

针对三维张量，4.1节步骤(4)每迭代一次，就把原始张量X的每个元素值分散到A，B，C 3个矩阵中，即按式(2)进行映射。此时，随机填充的缺失数据值和已知数据的值都映射到矩阵A，B，C中，并且在一定程度上混合了，即矩阵A，B，C中每个元素值不仅与已知数据相关，而且与随机填充的缺失数据相关。

由于数据具有一定的潜在结构，因此每个缺失位置的元素值根据第一轮迭代后的A，B，C值按照式(2)还原后，会含有一定的新信息，这些信息就是通过CP分解模型挖掘出的理论填充值。

重复4.1节的步骤(4)，每迭代一次，都会根据已知数据不断修正填充值。由于CP分解的唯一性，因此每迭代一次，填充值的变化会越来越小，直到收敛。

5 实验结果与分析

5.1 算法准确性

为了验证算法的准确性，本文实验将部分数据丢失的BGR图像像素值写入张量X中，X的第一维为通道数(BGR图像时长度为3)，第二三维为图像的高度和宽度，xijk表示第i通道在位置(j,k)处的像素值。实验结果如图2、图3所示。图2(a)为按三维形式存储的挖掉一块数据的原始图像，图2(b)为CP-WOPT算法填充结果，图2(c)为CPWF算法填充结果。由于CP-WOPT算法不够准确，因此图2(b)中填充的效果很不好，当局部块缺失时，该算法不能准确挖掘已知数据的潜在结构去填充缺失部分。实验结果表明，对于局部整块缺失的多维数据，CPWF算法填充效果很好。

图2 R=4时图像填充效果

图3(a)为按三维形式存储的添加30%噪声的原始图像，图3(b)为CP-WOPT算法填充结果，图3(c)为CPWF算法填充结果。被噪声污染的部分被认为是数据缺失的部分。显然，CP-WOPT算法填充有一些效果，但是帽子和肩膀部分的填充仍然不是很好。而本文提出的CPWF算法填充效果明显比CP-WOPT算法要好，不仅平滑，而且细节更明显。该实验表明，本文提出的CPWF算法对于离散型缺失的多维数据填充效果同样非常好。

图3 R=11时图像填充效果

5.2 算法效率

针对图2、图3中三维形式的数据，CP-WOPT算法和CPWF算法运行时间如表1所示。本文所有实验数据都在联想Y460N笔记本上测试运行，CPU为i3 380M，2.53 GHz。内存4 GB，64位Win7操作系统。由表1可以看出，CPWF算法运算速度明显比CP-WOPT算法快。

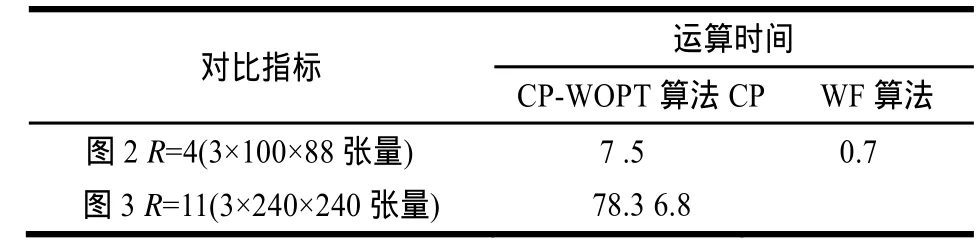
表1 C P-WOPT和CPWF算法运行时间比较 s

6 结束语

本文提出一种基于张量分解的多维数据填充算法，利用张量分解中CP分解模型的结构特性和分解的唯一性，实现了对多维数据中缺失数据的有效填充。实验结果证明，不管是局部数据整块缺失还是全局离散缺失，本文提出的CPWF算法都可以很好地填充缺失数据，不仅比CP-WOPT算法准确，而且运行速度更快。对于没有规律或者规律不明显的多维数据，如果是全局离散缺失，本文算法仍然可以很好地填充，但当局部数据整块缺失时，算法效果并不理想，因此，需要作进一步研究。另外，本文中的R值需要手动调整以达到最佳填充效果，如果取值过大，填充效果反而不好，因此，如何选取一个合适的R值也需要作进一步研究。

[1] Smilde A, Bro R, Geladi P. Multi-way Analysis: Applications in the Chemical Sciences[M]. [S. l.]: Wiley, 2004.

[2] Pearson R K. The Problem of Disguised Missing Data[J]. ACM SIGKDD Explorations Newsletter, 2006, 8(1): 83-92.

[3] Witten I H, Frank E. Data Mining: Practical Machine Learning Tools and Techniques with Java Implementations[M]. 2nd ed. [S. l.]: Morgan Kaufmann, 2005.

[4] Han Jiawei, Kamber M. Data Mining Concepts and Techniques[M]. 2nd ed. [S. l.]: Morgan Kaufmann, 2006.

[5] Nocedal J, Wright S J. N umerical O ptimization[M]. [S. l.]: Springer, 1999.

[6] 邹 薇, 王会进. 基于朴素贝叶斯的EM缺失数据填充算法[J]. 微型机与应用, 2011, 30(16): 75-77, 81.

[7] Acar E, Dunlavy D M, Kolda T G, et al. S calable Tensor Factorizations wi th Missing Data[C]//Proceedings of SI AM International Co nference on Da ta Mining. Colu mbus, US A: [s. n.], 2011: 41-56.

[8] Kolda T G, Bader B W. Tensor Decompositions and Applications[J]. SIAM Review, 2009, 51(3): 455-500.

[9] 廖志芳, 李 玲, 刘丽敏, 等. 三部图张量分解标签推荐算法[J]. 计算机学报, 2012, 35(12): 2625-2632.

[10] Golub G H, V anloan C F. Matrix C omputations[M]. [S. l.]: Johns Hopkins University Press, 1996.

[11] Kruskal J B. Rank, Decomposition, and Uniqueness for 3-way and N-way Arrays[M]. Amsterdam, the Netherlands: North-Holland Publishing Co., 1989: 7-18.

[12] Hastad J. Tensor rank is NP-complete[J]. Journal of Algorithms, 1990, 11(4): 644-654.

编辑 陆燕菲

Multi-dimensional Data Filling Algorithm Based on Tensor Decomposition

ZHU Yan-jun, WU Xiang-yang

(School of Computer Science and Technology, Hangzhou Dianzi University, Hangzhou 310018, China)

On the multi-dimensional data an alysis and processing, data with missing or unknown values is ubiquitous. How to use the potential structure of the known data to reconstruct the missing data is an urgent problem to be solved. Previously, the missing data filling mostly aims at low-dimensional da ta in matrix or vector format, while research on high-dimensional data above 3D is very few. To solve this problem, this paper proposes a multi-dimensi onal data filli ng algorithm based on tensor deco mposition, adequ ately using te nsor decomposition’s structure and uniqueness of CP model, to realize the multi-dimensional data filling effectively. Filling image with missing data stored in 3D format by experiment and comparison with CP-WOPT algorithm, it proves that this algorithm is not only accurate but also rapid.

missing data filling; tensor decomposition; mulit-dimensional data filling; multi-dimensional data analysis; multi-dimensional data processing; image inpainting

10.3969/j.issn.1000-3428.2014.05.010

国家自然科学基金资助项目(61003193)；浙江工业大学重中之重学科开放基金资助项目。

朱彦君(1988－)，男，硕士研究生，主研方向：大规模数据处理，图形图像处理；吴向阳，副教授、博士。

2013-05-09

2013-06-09E-mail：156372288@qq.com

1000-3428(2014)05-0045-04

A

TP301