二值命题逻辑中逻辑理论的计量化及应用
2014-08-05王菊花
李 骏,王菊花
兰州理工大学 理学院,兰州 730050
二值命题逻辑中逻辑理论的计量化及应用
李 骏,王菊花
兰州理工大学 理学院,兰州 730050
1 引言
数理逻辑的特点在于形式化与符号化,它和计算数学有着截然不同的风格:前者注重形式推理而后者重视数值计算;前者强调严格论证而后者允许近似求解。逻辑推理方法在诸如定理的自动证明、知识推理、逻辑程序设计等多个领域得到了广泛的应用[1-2],数值计算则似乎是远离形式推理的完全不同的方法。为填补这一鸿沟,王国俊教授等将程度化思想引入到数理逻辑之中建立起了计量逻辑学的基本理论[3-6],如今已在包括Lukasiewicz和R0系统在内的各种命题逻辑系统中构造出了相应的逻辑度量空间,从而将近似推理引入到素以严格的形式化推理为特征的各种命题逻辑系统中(可参看文献[7-12])。
在计量逻辑学中,除了对单个公式进行计量化研究之外,学者们对理论自身的性质也十分关注,比如:文献[13-16]研究了理论的相容性和发散性等性质,并借助理论的发散度提出了理论的相容度概念,以此来区分不同理论相容程度的大小,进而达到区分不同理论好坏程度的目的。另外,在命题逻辑中经常要研究从某个命题之集Γ(即,理论)到另一个命题A的推演,即,从前提信息之集Γ推出某个结论A来。但是在现实推理中,可能所获取的信息不足以将A作为理论Γ的逻辑结论推出来,这时就需考察理论Γ在多大程度上能推出结论 A来,即研究从理论Γ出发的近似推理,这也就涉及理论Γ本身的好坏问题,如果能够给出一个评判理论Γ本身可靠程度的直接方法(或指标),这将为展开从前提信息集Γ出发的近似推理提供直接的依据。文献[17]首次在命题逻辑系统中引入了理论Γ的真度概念来刻画理论的可靠程度,但那里是把理论Γ的全体逻辑结论真度的下确界值作为理论Γ的真度,这种方法首先损失了理论Γ的结论中真度值较大的那些结论提供的信息;其次,这种方法借助了理论Γ本身以外的东西(即Γ的结论)来定义理论Γ的真度是不尽合理的,因为当理论Γ本身不可靠时,它的逻辑结论就更加不可靠;第三,当理论Γ退化为只含一个公式(比如:B)时,在多值逻辑中,按文献[17]中的方法计算出的理论Γ的真度并不等于公式B的真度。因此,给出一个能克服以上缺陷的评判理论可靠程度的新方法,是有价值的研究课题。
本文在二值命题逻辑系统L中,首先借助势为2的均匀概率测度空间的无穷乘积,通过计算理论Γ的全体模型占整个赋值空间的测度来定义理论Γ的真度,该定义是文献[3]中公式真度定义的自然推广,即:当理论Γ退化为只含一个公式(比如:B)时,理论Γ的真度就等于公式B的真度。其次,利用理论的真度定义了理论与理论之间的相似度和伪距离,并给出理论的真度在近似推理及其在描述理论的发散度、相容度等方面的应用。值得指出的是:当理论退化为单个公式时,本文关于理论所建立的计量化结果正是文献[3]中相应的结果。
2 预备知识
设S={p1,p2,…},F(S)是由S生成的(﹁,→)型自由代数。S中的元叫原子命题,F(S)中的元称为公式(或命题)。在L={0,1}中规定:﹁0=1,﹁1=0,a→b=0当且仅当a=1且b=0,则{0,1}成为一个(﹁,→)型代数。称(﹁,→)型同态v∶F(S)→{0,1}为F(S)的一个赋值。以Ω记F(S)上全体赋值之集。
定义1[5]设 A∈F(S),若∀v∈Ω,v(A)=1,则称 A为重言式,记为:╞A;若∀v∈Ω,v(A)=0,则称 A为矛盾式;若∀v∈Ω,都有v(A)=v(B),则称 A与B逻辑等价,记作:A≈B。
定义2[5]若Γ⊆F(S),则称Γ为理论。设 A∈F(S),则从理论Γ到 A的一个推演是一个有限的公式序列A1,A2,…,Am,其中,Am=A,且∀i≤m,Ai是公理或者Ai∈Γ或者存在 j,k<i,使得 Ai是由 Aj和 Ak运用MP规则而得到的结果,称A为Γ-结论,记作:Γ├A,m叫作从Γ到A的推演长度,进一步,若Γ=Φ(空集),则称A为定理,简记为:├A。
下文以0-记任一矛盾式,以D(Γ)来记全体Γ-结论之集,以T记全体理论之集,即
D(Γ)={A|A∈F(S),且Γ├A},T={Γ|Γ⊆F(S)}
设 Γ∈T,若 0-∈D(Γ),则称 Γ是不相容的理论。另外,若Γ只含一个公式A,即Γ={A},则将Γ简记为:Γ=A。
定义3设Γ∈T,v∶F(S)→{0,1}是赋值,若∀Ai∈Γ,都有v(Ai)=1,则称v是Γ的模型,记为v|=Γ或v(Γ)=1;若v不是Γ的模型,则简记为v(Γ)=0;如果对每个v∈Ω,均有v|=Γ,则称Γ是完全相容的,简记为|=Γ;若每个v∈Ω,都有v(Γ)=0,则称Γ是完全不相容的。
定义4设Γ1,Γ2∈T,如果对每个v∈Ω,均有v(Γ1)= v(Γ2),则称Γ1与Γ2逻辑等价,记作:Γ1≈Γ2。
注1显然,当Γ1与Γ2都退化为只含单个公式时,理论之间的逻辑等价概念正是公式之间逻辑等价的概念。
定理1设Γ∈T,则Γ是完全相容的当且仅当Γ全由定理组成。
证明 设Γ是完全相容的,则∀v∈Ω,∀A∈Γ,都有v(A)=1,从而∀A∈Γ,A都是重言式,由完备性定理知∀A∈Γ,A都是定理;反过来,若∀A∈Γ,A都是定理,则A都是重言式,从而∀v∈Ω都有v(A)=1成立,即∀v∈Ω,均有v|=Γ,因此Γ是完全相容的。
3 理论的真度

定义7[3]设v∈Ω,记v(pk)=vk(k=1,2,…),则无穷维向量v={v1,v2,…}∈X,这里X由定义6确定。反之,设v={v1,v2,…}∈X,则由v唯一确定Ω中的一个赋值v,这里v(pk)=vk(k=1,2,…)。令φ(v)=v,则φ∶Ω→X是从Ω到X的一一的满射,称φ为Ω的测度化映射。
定义8设Γ∈T,令

称τ(Γ)为理论Γ的真度。


(2)由于在实际推理中,推理的前提信息之集(即理论Γ)通常都是有限集,Γ中的公式用到的原子公式自然只有有限多个。因此下文中若无声明,都假定构成理论Γ的公式中只用到有限多个原子公式。
(3)定义8中,若Γ={B},B∈F(S),则有

式(4)右边正是文献[3]中公式B真度的定义式,即τ({B})= τ(B)。可见本文所给出的理论的真度定义是公式真度定义的自然推广。

下面的引理是文献[5]中已给出的本文即将用到的几个结果:
引理1[1]设A、B∈F(S),则
(1)A是重言式当且仅当τ(A)=1,A是矛盾式当且仅当τ(A)=0。
(2)若A≈B,则τ(A)=τ(B)。
(3)若├A→B,则τ(A)≤τ(B)。
(4)τ(﹁A)=1-τ(A)。
(5)τ(B)≥τ(A)+τ(A→B)-1。
定理2设 Γ∈T,若 Γ={A1,A2,…,An}是有限理论,则τ(Γ)=τ(A1∧A2∧…∧An);若Γ={A1,A2,…,Ak,…}是无穷理论,则τ(Γ)=τ(A1∧A2∧…∧An)。
证明 设Γ={A1,A2,…,An}是有限理论,则由定义8和注解2知:


定理3设Γ∈T,则
(1)τ(Γ)=1当且仅当Γ为完全相容理论。
(2)τ(Γ)=0当且仅当Γ为完全不相容的理论。
证明(1)若Γ是完全相容理论,则由定理1知Γ全由定理组成,从而∀v∈Ω,∀Ai∈Γ,都有v(Ai)=1,因此∀v∈Ω,都有v|=Γ,故{v∈X|φ(v)=v,v∈Ω,且v|=Γ}=X,从而

反过来,若τ(Γ)=1,假设Γ不是完全相容的理论,则有 v∈Ω 使 v|=Γ不成立,设 pi1,pi2,…,pin是构成 Γ所用到的全体原子公式,令v(pik)=vik(k=1,2,…,n)。则(vi1,vi2,…,vin)∉E,这里 E由注2给出。因为 μi1({vi1})× μi2({vi2})×…×μin({vin})=,所以(μi1×μi2×…×μin)(E)≤1-。从而由定义5和定义8知μ([Γ])≠1,从而τ(Γ)≠1,矛盾!因此,Γ为完全相容理论。
(2)设 Γ为完全不相容的理论,则 ∀v∈Ω,都有v|=Γ不成立,从而[Γ]=ϕ(空集),故τ(Γ)=μ(ϕ)=0。
反过来,假设Γ不是完全不相容理论,则有v∈Ω使v|=Γ成立。设 pi1,pi2,…,pin是构成Γ所用到的全体原子公式,令v(pik)=vik(k=1,2,…,n)。则(vi1,vi2,…,vin)∈E,这里 E由式(3)确定。因为 μi1({vi1})×μi2({vi2})×…× μin({vin})=所以 (μi1×μi2×…×μin)(E)≥。从而由式(1)及式(3)知μ([Γ])≠0,故τ(Γ)≠0,矛盾!因此,Γ为完全不相容理论。
定理4设Γ1,Γ2∈T,若Γ1≈Γ2,则τ(Γ1)=τ(Γ2)。
证明 因为Γ1≈Γ2,所以∀v∈Ω,有v(Γ1)=v(Γ2),即∀v∈Ω,v|=Γ1当且仅当 v|=Γ2,所以 [Γ1]=[Γ2],从而τ(Γ1)=τ(Γ2)。
4 理论真度的应用
本章将给出理论的真度在描述理论的发散度和相容度等方面的一些应用,先给出文献[5]中已有的一些结果。

首先,若A∈D(Γ),则可取B为任意一个定理(当然有 B∈D(Γ)),此时由 (A→B)∧(B→A)≈A,从而τ((A→B)∧(B→A))=τ(A)知

其次,∀A,B∈D(Γ),由A→(B→A)和B→(A→B)是公理可知A→B∈D(Γ),且B→A∈D(Γ),从而(A→B)∧(B→A)∈D(Γ),故
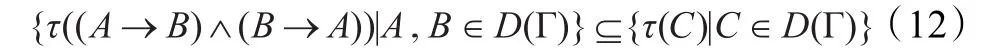
由式(11)和式(12)知式(10)成立,从而式(9)成立。
定理6设Γ∈T,则div(Γ)=1-τ(Γ)。
证明 若Γ={A1,A2,…,An}是有限理论,则∀A∈D(Γ),由├(A1∧A2∧…∧An→A),从而由 τ(A1∧A2∧…∧An)≤τ(A)知

从而由定理3和定理5可知div(Γ)=1-τ(Γ)。若Γ= {A1,A2,…,Ak,…}是无穷理论,则对任意的自然数n,A1∧A2∧…∧An∈D(Γ),令
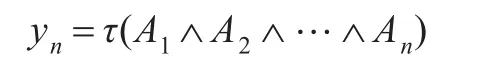
则数列{yn}单调递减且有下界0,从而数列{yn}极限τ(A1∧A2∧…∧An)存在,因此

注3文献[5]中关于一般的理论给出了刻画其相容程度的η-相容度,将本文定理6中发散度的简化公式代入η-相容度的表达式中就可得到简化的η-相容度计算公式。
定理8设Γ∈T,若τ(Γ)=α,则∀B∈Γ,都有τ(B)≥α。
证明 若Γ={A1,A2,…,An}是有限理论,则由定理3知τ(Γ)=τ(A1∧A2∧…∧An),又∀Ai∈Γ,由├A1∧A2∧…∧An→Ai和引理1(3)可知τ(Ai)≥τ(Γ)=α,结论成立。
若 Γ={A1,A2,…,Ak,…}是无穷理论,由定理1知τ(Γ)=τ(A1∧A2∧…∧An)。 又 ∀An∈Γ ,由├A1∧A2∧…∧An→An知 τ(A1∧A2∧…∧An)≤τ(An),令 yn= τ(A1∧A2∧…∧An),由数列 {yn}单调递减且 τ(Γ)=τ(A1∧A2∧…∧An)知τ(An)≥τ(Γ)=α,从而结论对无穷理论也成立。
定理9设Γ∈T ,α>0,τ(Γ)=α,A是Γ的长度为n的结论,则

这里,un是斐波那契数列的第n项,即

且有u1=u2=1,un+un+1=un+2,n=1,2,…。
证明 采用数学归纳法来证明。
当n=1时,因为A为公理或A∈Γ所以由引理1(1)和定理7知τ(A)≥α,又式(13)右端un(α-1)+1=α-1+ 1=α,因此式(13)成立。设n≤k时式(13)成立,A是Γ的长度为k+1的推论,推演序列为A1,A2,…,Ak,A。不妨设 A∉Γ,A也不是公理,则有i≤k,j≤k,使得 A是由Ai和Aj通过运用MP规则而得的结果,由归纳假设得:

不妨设i<j,则 j≤k,i≤k-1,注意到(α-1)≤0,从而由引理1(5)可得:即式(13)当n=k+1时也成立,定理得证。
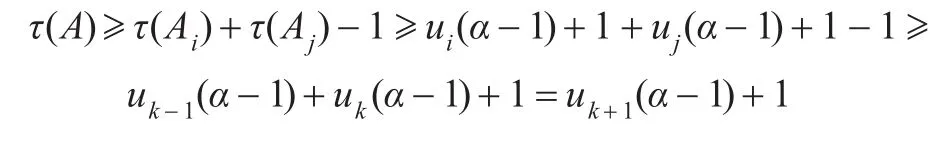
注4由定理9知,若推理的前提信息之集Γ的真度为α,则其推理长度为n的逻辑结论的真度不小于un(α-1)+1,比如:若τ(Γ)=1,则对任意的n,Γ的推演长度为n的逻辑结论的真度均为1;若τ(Γ)≥0.99,则Γ的推演长度为6的逻辑结论的真度均不小于0.92。
5 结束语
本文在二值命题逻辑系统中,借助势为2的均匀概率测度空间的无穷乘积,通过计算理论Γ的全体模型占整个赋值空间的测度定义了理论Γ的真度,并给出理论的真度在描述理论的发散度、相容度等方面的应用,值得指出的是:当理论退化为单个公式时,本文关于理论所建立的计量化结果正是文献[3]中相应的结果。关于如何将本文结果推广到多值以至于连续值命题逻辑系统,将另文讨论。
[1]Rosser J B,Turquette A R.Many-valued logic[M].Amsterdam:[s.n.],1952.
[2]Ying M S.A logic for approximate reasoning[J].Journal of Symbolic,1994,59:830-837.
[3]Wang G J,Fu L,Song J S.Theory of truth degrees of propositions in two-valued logic[J].Sci China Ser A-Math,2002,45:1106-1116.
[4]Wang G J,Zhou H J.Quantitative logic[J].Information Sciences,2009,179(3).
[5]王国俊.数理逻辑引论与归结原理[M].2版.北京:科学出版社,2006.
[6]王国俊,宋建社.命题逻辑中的程度化方法[M].电子学报,2006,34(2):252-257.
[7]Wang G J,Hui X J.Randomization of classical inference patterns and its application[J].Science in China:Ser F,2007,50(6):867-877.
[8]Zhou H J.Borel probabilistic and quantitative logic[J].Science China Information Sciences,2010,53:1-12.
[9]Li J,Wang G J.Theory of truth degrees in logic system[J].Science in China:Ser E,2006,36(6):631-643.
[10]李骏,邓富喜.n值S-MTL命题逻辑系统中公式真度的统一理论[J].电子学报,2011,39(8):1864-1868.
[11]王国俊,李璧镜.Lukasiweicz n值命题逻辑中公式的真度理论和极限定理[J].中国科学 E辑:信息科学,2005,35(6):561-569.
[12]李骏,王国俊.基于支持度理论的广义MP问题的形式化解[J].电子学报,2008,36(11):2190-2194.
[13]Zhou X N,Wang G J.Consistency degrees of theories in some systems of propositional fuzzy logic[J].Fuzzy Sets and Systems,2005,152:321-331.
[14]Wang G J,Zhang W X.Consistency degrees of finite theories in Lukasiewicz propositional fuzzy logic[J].Fuzzy Sets and Systems,2005,149(2):275-284.
[15]Zhou H J,Wang G J.A new consistency index based on deduction theorems in several logic systems[J].Fuzzy Sets and Systems,2006,157(3):427-443.
[16]Wang G J,She Y H.Topological description of divergency and consistency of two-valued propositional theories[J].Acta Mathematica Sinica:Chinese Series,2007,50(4):841-850.
[17]王国俊,高香妮.命题逻辑系统中理论的真度概念及其应用[J].陕西师范大学学报:自然科学版,2009,37(5):1-6.
[18]Halmos P R.Measure theory[M].New York:Springer-Verlag,1974.
LI Jun,WANG Juhua
School of Science,Lanzhou University of Technology,Lanzhou 730050,China
By means of infinite product of uniformly distributed probability spaces of cardinal 2,this paper introduces the concept of truth degree of a logical theoryΓby computing the measure of all models ofΓin the valuation spaces.Simplified methods to compute the divergent degree and the consistent degree of a logical theory are given and the expression to estimate the truth degree of logical conclusions from the truth degree of its premise set is obtained.
quantitative logic;logical theory;truth degree of logical theory;consistency degree
在二值命题逻辑系统中,利用势为2的均匀概率测度空间的无穷乘积,通过计算理论Γ的全体模型占整个赋值空间的测度定义了理论Γ的真度,进而利用理论的真度简化了理论的发散度和相容度的计算公式,给出了由推理的前提集的真度估计其逻辑结论真度的表达式。
计量逻辑学;逻辑理论;理论的真度;相容度
A
O141.1
10.3778/j.issn.1002-8331.1301-0205
LI Jun,WANG Juhua.Quantification of logic theory in two-valued propositional logic and its applications.Computer Engineering and Applications,2014,50(24):42-46.
国家自然科学基金(No.11261032);兰州理工大学博士基金资助项目。
李骏(1972—),男,博士,副教授,硕士研究生导师,研究领域:非经典数理逻辑、不确定性推理;王菊花(1987—),女,硕士研究生,研究领域:不确定性推理。
2013-01-21
2013-04-22
1002-8331(2014)24-0042-05
CNKI网络优先出版:2013-05-21,http∶//www.cnki.net/kcms/detail/11.2127.TP.20130521.1027.004.html
