工程结构可靠度指标的计算方法

陈海彬，郑玉，佟晓君，王力

（河北联合大学 建筑工程学院，河北省地震工程研究中心，河北 唐山063009）

0 引 言

工程结构可靠性理论对结构设计能否符合安全可靠、耐久适用、经济合理、技术先进、确保质量要求，起着重要的作用。近年来，随着科学技术的进步与发展，结构可靠度理论及其方法在结构设计、结构安全评估、结构安全鉴定等诸多领域都得到了有效地运用与发展［1－7］。1工程结构中规定用可靠指标来度量结构的可靠性，目前确定结构可靠指标的方法主要有：中心点法、验算点法、映射变换法、使用分析法、蒙特卡洛法及随机有限元法等。工程上最常用的方法为验算点（即JC法），它的特点是能够考虑非正态变量，在计算工作量增加不多的条件下，可对可靠指标β进行精度较高的近似计算。但是，在JC法计算过程中由于可靠指标与设计验算点相互耦合，彼此制约，给数值计算带来一定的难度。因此，寻求一种相对简洁的方法进行可靠度计算是目前工程上所需要的。

设计验算点是在满足极限状态方程条件下，最可能出现的荷载效应和抗力效应随机变量组合，同时也是确定结构可靠度的基本要素。本文基于这一物理涵义并应用最大似然原理，给出了随机变量分别为任意分布情况时确定求解结构设计验算点的最大似然法，利用加权最小二乘方法，给出了一种求解可靠性指标的新方法，并结合具体工程算例给出了确定结构可靠指标的方法。

1 确定设计验算点的似然方程

设X1，X2，…，Xn为结构中n个相互独立的随机变量，且分别服从任意分布，其相应的概率密度函数为fX1（x1），fX2（x2），…，fXn（xn），设x1，x2，…，xn是 相 应 于 样 本X1，X2，…，Xn的 一 个 样 本 值，则 随 机 点落在点 （x1，x2，…，xn）的边长分别为dx1，dx2，…，dxn的n维立方体领域内的概率为：

设由随机变量表示的结构功能函数为：

极限状态方程为：

依照设计验算点的物理意义，在满足式（3）条件下随机变量X取值落在点x＊1，x＊2…，x＊n的任意小的邻域时应发生最大概率，构造拉格朗日似然函数为：

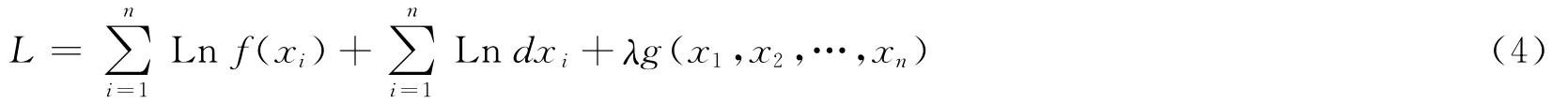
式中：λ为拉格朗日乘子，对xi（i＝1，2，…，n） 和λ分别求偏导，并令其等于零有：

经整理得：

l可取1到n之间的任意值。定义为分布密度特征值，（5）式可写为：

联立上面（8）、（9）n个方程，可解出，即为结构的设计验算点。

如果独立随机变量为X1，X2，…，Xn都服从正态分布，可用下式直接计算可靠指标

如果独立随机变量为X1，X2，…，Xn不服从正态分布，可通过当量正态化的方法按下式计算

2 二维正态分布可靠性指标的计算方法

国际结构安全度联合会（JCsS）推荐使用，验算点法，由于其克服了中心点法的缺点，并且保持了二阶矩形式和极限状态函数表达式之间的关系，成为结构可靠度理论的重要组成部分。但是，当极限状态函数z为非线性时，通过z＝0的某一超切平面进行近似，从而可能引起可靠性指标计算值偏高，导致工程结构安全隐患。

设

则有：

设直线方程：

其中：a、b为回归系数。

令

由方程组

可以得到：

式中：

P1、P2和P3分别为点和验算点的概率，则有：

求得新的可靠性指标为：

综合考虑极限状态方程的各种情况，所以二维正态分布的可靠性指标为：

3 工程算例

（1）由分布密度特征值定义，可以得到

（2）任取l＝2并代入式（8）、（9）得到

联立上两式，运用数值方法可解出设计验算点值：

按式（10）计算出可靠性指标：

（3）由式（13）、（14）可以得到：

由三点求得加权权数为：

由式（16）、（17）可以得到回归系数为：

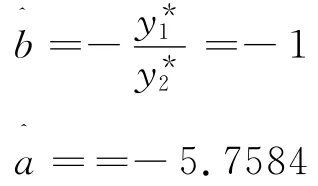
求得新的可靠性指标为：

所以可靠性指标为：

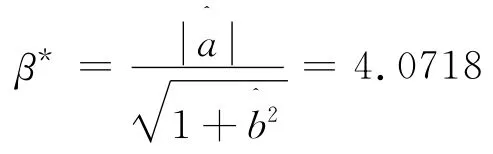
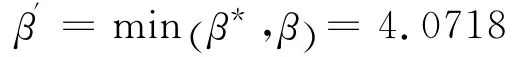
4 结 论

（1）在满足极限状态方程的条件下，利用最大似然原理，提出一种确定设计验算点及可靠性指标的最大似然方法。文中提出的方法计算相对简洁，物理意义比较明晰，能够满足目前工程上可靠性计算的要求。

（2）利用加权最小二乘法，给出了一种求解二维正态分布的可靠性指标方法，该方法求得的可靠性指标更加接近真值，从而减少安全隐患。此方法可以进一步推广到多维正态分布，甚至多维非正态分布情况。

（3）将本文方法应用到工程算例中，表明最大似然方法在求解可靠性指标及设计验算点的过程中避免了传统方法的反复迭代，简化了计算过程。加权最小二乘方法得到的可靠性指标更精确，更安全。

［1］ 徐军，郑颖人.工程结构可靠度指标计算的混沌搜索方法［J］.工程力学，2002，19（3）：6－8.

［2］ 赵国藩.工程结构可靠性理论与应用［M］.大连：大连理工大学出版社，1996.

［3］ 章光，朱维申，白世伟.计算近似失效概率的最大熵密度函数法［J］.岩石力学与工程学报，1995，14（2）：119－129.

［4］ 冷伍明，赵善悦.用不求导数的最优化计算可靠度指标［J］.西南交通大学学报，1993，20（2）：58－63.

［5］ 洪昌华，龚晓南.相关情况下Hasofer－Lind可靠度指标的求解［J］.岩土力学，2000，21（1）：68－75.

［6］ 徐军，邵军，郑颖人.遗传算法在岩土工程可靠度分析中的应用［J］.岩土工程学报，2000，22（5）：586－589.

［7］ 李兵，蒋慰孙.混沌优化方法及其应用［J］.控制理论与应用，1997，14（4）：613－615.

［8］ 李扬海，鲍卫刚.公路桥梁结构可靠度与概率极限状态设计［M］.北京：人民交通出版社，1997.