矮塔斜拉桥塔墩梁固结实体分析
2014-08-05曹伟宏石少华
曹伟宏,石少华
(1.河北联合大学 建筑工程学院,河北省地震工程研究中心,河北 唐山063009;2.核工业西南勘察设计研究院,四川 成都,610061)
0 引 言
矮塔斜拉桥兼有斜拉桥与梁式桥的优点,造型美观、技术先进、造价低,近几年在我国得到了较好的发展[1-3]。由于采用塔墩梁固结体系,相比传统的塔梁固结形式,其受力更加复杂,固结部位除了承受巨大的轴向力和弯矩外,还承受由主梁传递的较大的竖向力和扭矩。同时,塔的刚度与墩的刚度相比于固结处梁的刚度变化较大,塔墩梁固结处的构造处理尤为关键,因此,通过三维实体模型对过人孔周边、塔梁固结处及墩梁固结部位的应力情况进行分析,研究塔墩梁固结部位的受力特性及其应力分布规律,这些关键部位的应力情况可以直接反应构造拟定是否合理及优化方向,这一分析对结构的安全可靠具有重要意义[4-9]。
拟建黄龙带矮塔斜拉桥位于大广高速公路D3合同段,上跨黄龙带水库,桥梁左幅结构中心线位于R=1786.5m的圆曲线上;右幅桥梁结构中心位于R=1809.5m的圆曲线上,横向单面坡3%。主桥采用(108+208+108)m矮塔混凝土斜拉桥,主梁左右分修,在塔墩梁固结处通过横梁连成一个整体,横梁厚度4.8 m,采用三柱式塔,三柱式桥墩。结构体系采用塔墩梁固结体系,边墩处设置支座。如下图1所示。
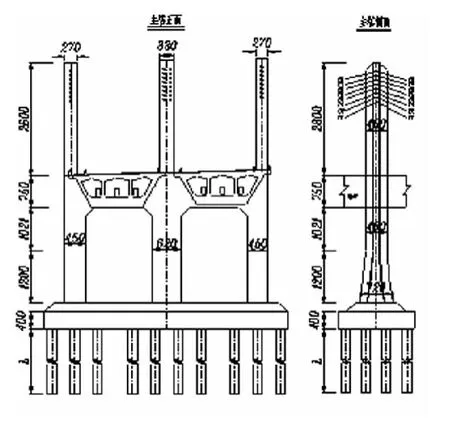
图1 主塔截面图
1 有限元模型
本文首先采用MIDAS/CIVIL 2006建立全桥梁单元模型,对大桥进行整体受力分析计算,再采用MIDAS/FEA对塔梁墩固结部位建立局部实体模型,进行详细应力分析。建立实体模型时,主梁取0号块、1号块、2号块、3号块,共计26m,塔墩取至承台位置,塔高取17m,故此取值范围离固结部位已取至足够长度,可以排除圣维南效应对塔墩梁固结部位受力的影响。模型中混凝土采用实体单元中的六面体单元进行模拟,横梁处横向预应力钢筋及主塔部分竖向预应力钢筋采用自动网格线直接钢筋单元方法进行模拟。对于主梁纵向预应力索,本文只模拟出锚固端在主梁0号块、1号块、2号块、3号块的部分,其余纵向预应力索的作用通过作用于梁端的受力进行模拟[10]。
实体模型共计83696个单元,69911个节点。图2为划分网格的有限元模型。
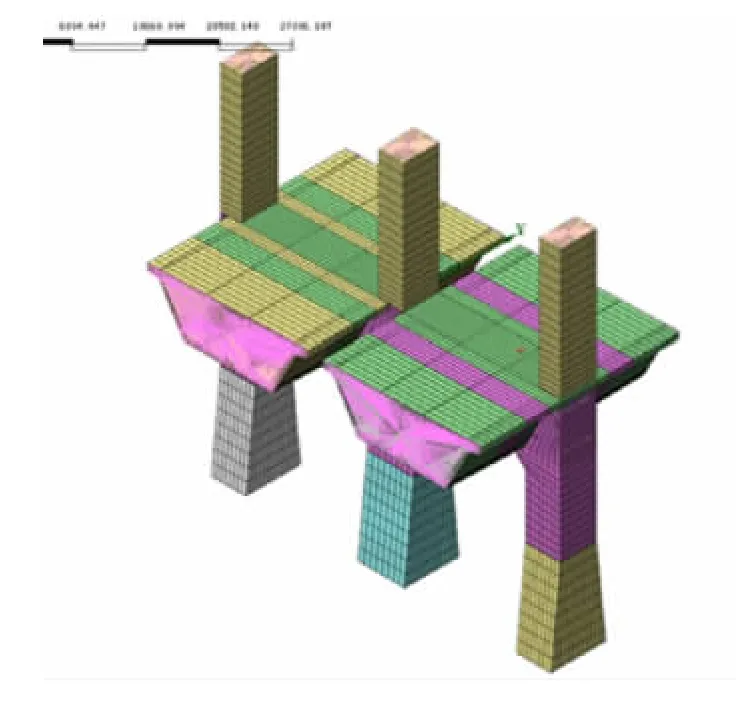
图2 塔墩梁固结有限元模型
2 边界和荷载
由于本文研究塔梁墩固结部位的局部应力,故边界条件采用桥塔底部固结;荷载为通过MIDAS/CIVIL 2006梁单元模型中得到的一组不利荷载。由于实体单元无法直接施加荷载,故采取在构件需施加荷载的截面形心部位建立一个节点(主节点),然后跟其他受力节点耦合,形成刚性区域,然后直接将弯矩、剪力和轴力施加到主节点,即形心节点。这种模拟弯矩的方式将导致梁端应力情况发生变化,在端部截面会产生明显端部效应,但本文研究内容为塔墩梁固结部位详细应力,根据圣维南原理,在弹性体的小部分边界上,原力系用另一个静力等效力系代替,只引起引小部分边界附近区域的应力发生变化,离开此区域较远处的应力不发生变化。故该方法采用在预加力截面施加外力的方式对塔墩梁固结部位应力影响很小,是可行的。
本文提取了塔顶处及左右幅大小里程3号截面处恒载+活载作为不利荷载组合,其具体数值见表1。
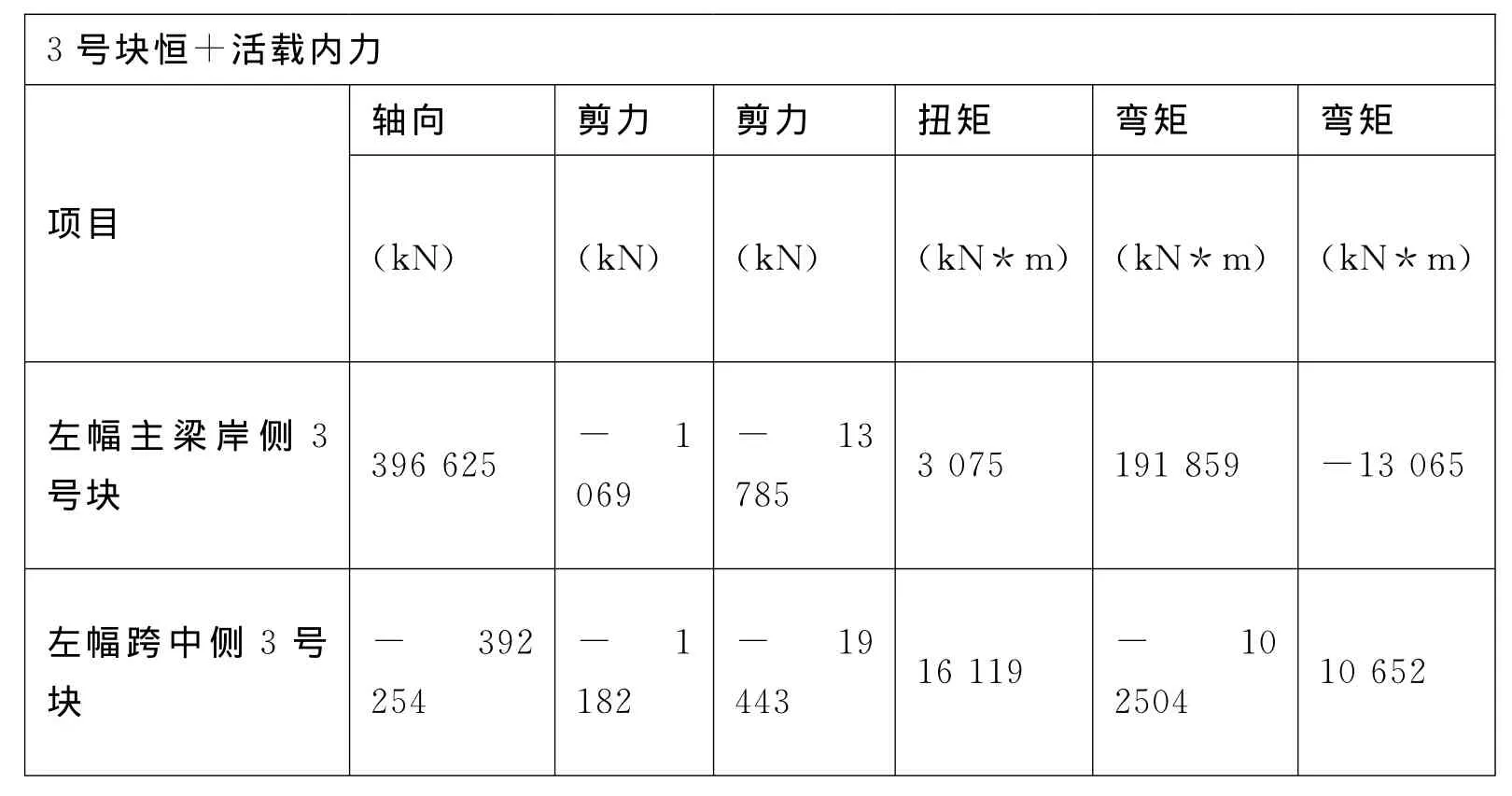
表1 最不利工况内力表

号块 401 369 1 372 - 14 392 6 913 224 466 22 215右幅主梁岸侧3右幅中侧3号块 - 398 551 1 403-19 994 16 377-141 338 -14 450 17m高处塔柱恒+活载内力轴向 剪力 剪力 扭矩 弯矩 弯矩项目(kN) (kN) (kN) (kN*m) (kN*m) (kN*m)边塔柱 -37 427 - 1 513 -1 059 0 7 849 3 082小里程曲线内侧小里程中塔柱 -72 096 - 2 164 -1 747 -1 732 12 901 6 006小里程曲线外侧边塔柱 -37 203 -630 -1 237 0 8 358 117
3 不利荷载作用下计算分析结果
由于斜拉索竖向分力的累积和桥塔的巨大竖向荷载,对塔梁墩固结部位的应力分布产生了明显影响,为能够更加清楚简洁地读取和分析塔墩梁固结部位应力情况,本文钝化了除0号块以外主梁梁段及塔柱和10 m塔墩。本文所有应力结果均从上述钝化以后的计算模型中读取。
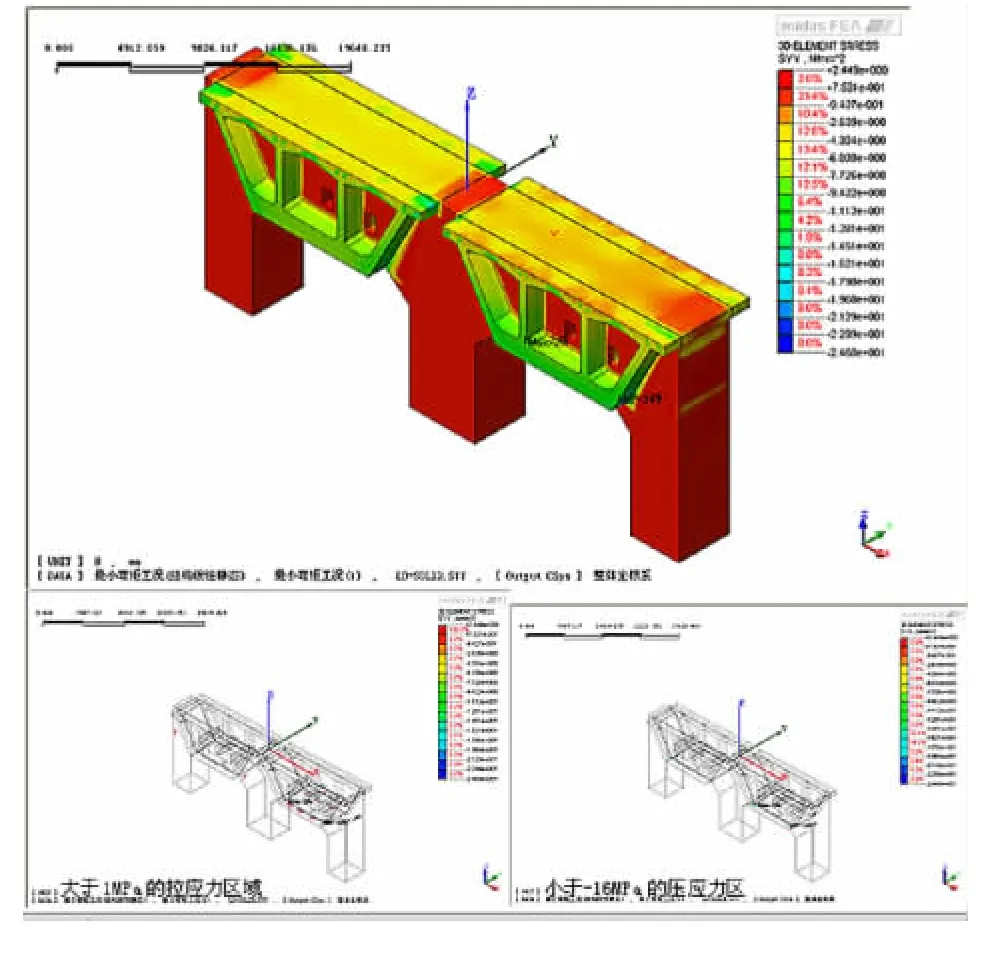
图3 纵向正应力分布图
3.1 纵向正应力
由图3可知,纵向正应力介于2.449MPa~ -24.68MPa之间,从图3可以看出,大于1MPa的区域很小,位于右幅梁体与横梁台阶处;小于-16MPa的区域很小,位于梁体与横梁台阶处;二者迅速衰减至-12.81~0.75MPa之间。
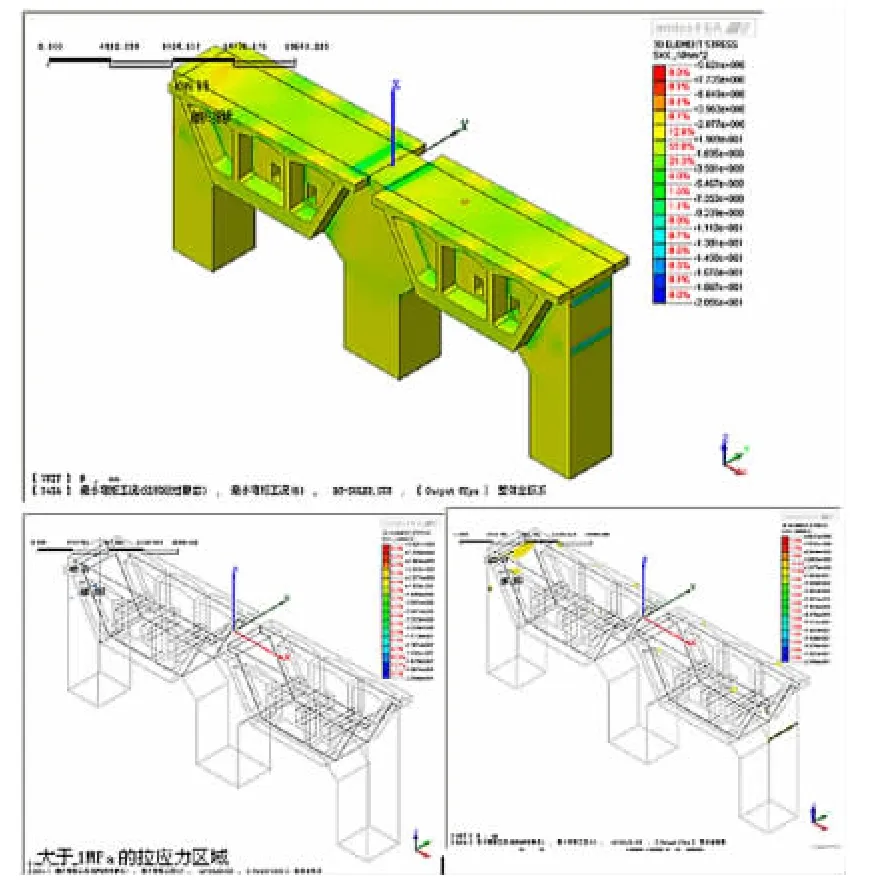
图4 横向正应力分布图
3.2 横向正应力
由图4可知,横向正应力介于-20.56~9.62MPa之间;从图4可以看出,大于1大于1MPa拉应力及小于-16MPa压应力的极值点均出现横向预应力锚固点附近,并且衰减很快,可以忽略,大部分应力介于-11.13~2.08MPa之间,满足规范要求。
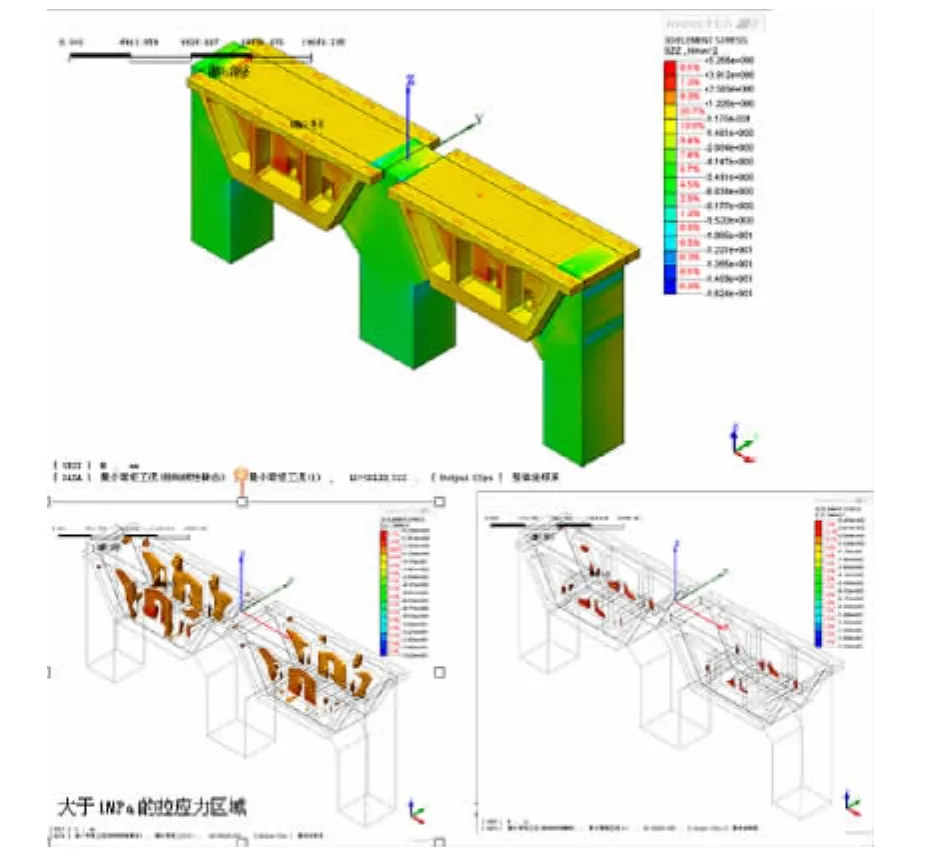
图5 竖向正应力分布图
3.3 竖向正应力
由图5可知,最大竖向拉应力出现在0号块横梁人孔附近,超过2MPa拉应力的区域较小,并且衰减较快,可适当调整构造尺寸,并施加竖向预应力来调整竖向应力。
3.4 主拉应力
由图6可知,在横向预应力锚固区与人孔区域存在较大的主拉应力,最大值为11.72MPa(最大值出现在预应力锚固区),此值为整个结构中所出现的最大主拉应力,是控制设计的一个重要指标。其余超过2 Mpa的区域基本上出现人孔附近以及梁体与横隔板的台阶处。
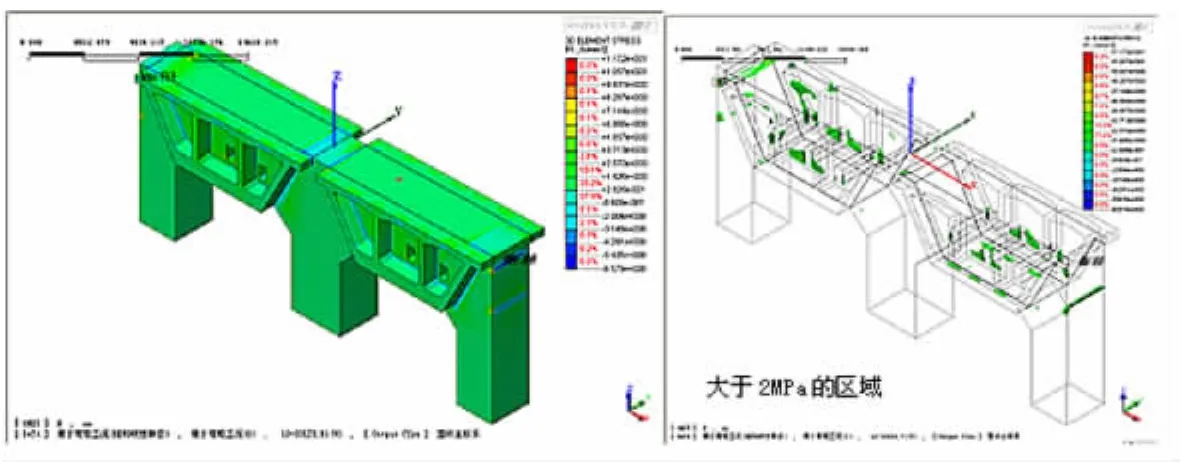
图6 主拉应力分布图
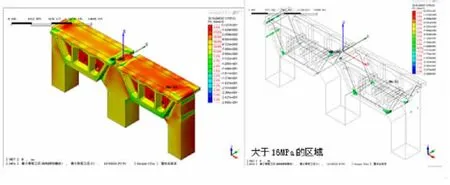
图7 主压应力分布图
3.5 主压应力
由图7可知,主压应力出现在梁体与横隔板台阶部位及横向预应力锚固区域,其值为-25.90MPa,此值为整个结构中所出现的最大主压应力,是控制设计的另一个重要指标。该处应力很快向周围过渡到-16.00MPa以内,除该局部表面应力外,其它部位的应力基本符合规范的要求。
3.6 应力结果分析
上述结果中极值应力大都出现在钢束锚固处、截面急剧变化处,这些部位由于结构自身刚度突变以及接触位置有限元法模拟失真,容易出现应力集中现象,但是这些应力分布范围很小,都呈点状分布,且极值点周边应力衰减很快。
4 结论与建议
通过对过人孔周边、塔梁固结处及墩梁固结部位的局部详细应力分析可知,黄龙带特大桥所采用的塔墩梁固结体系,总体上是一种受力比较适宜的方案,塔墩梁固结段结构设计合理,同时根据计算结果,提出以下几点建议:
(1)取消横梁与梁体不等高区域,横梁与梁体等高度设置。
(2)人孔处可加密钢筋布置,分散应力集中。
(3)增加竖向预应力在横梁处的布置。
(4)减少受力不利处人孔。
[1] 严国敏.现代斜拉桥[M].成都:西南交通大学出版社,1996.
[2] 王伯惠.斜拉桥结构发展和中国经验(上册)[M].北京:人民交通出版社,2003.
[3] 李亚东.桥梁工程概论[M].成都:西南交通大学出版社,2005.
[4] 曹忠强.异型矮塔斜拉桥塔墩梁固结部位应力分析[J].交通科技,2010(3):41-44.
[5] 黎耀,郑凯峰,陈力波.大跨矮塔斜拉桥塔墩梁固结部位详细应力计算分析[J].广东公路交通,2007(3):25-27.
[6] 虞庐松,朱东生.部分斜拉桥塔梁墩固结点局部应力分析[J].桥梁建设,2008(1):54-57.
[7] 曹忠强.矮塔斜拉桥全桥静动力计算和墩塔梁固结部位详细应力分析研究[D].成都:西南交通大学,2008.
[8] 王晓明,郝宪武,段瑞芳.斜拉桥塔梁固结处的空间应力分析[J].湖南交通科技,2007,33(1):84-88.
[9] 黄力,刘志权,石雪飞.大跨径斜拉桥塔墩梁固结处空间受力分析[J].石家庄铁道大学学报,2012(25)4:23-26.
[10] 徐芝纶.弹性力学[M].北京:高等教育出版社,2007.
