K-邻近条件下空间实体三维建模算法研究

倪 曙，方源敏，李国柱，陈 杰

(1.昆明市测绘研究院，云南昆明 650051；2.昆明理工大学国土资源工程学院，云南昆明 650093）

K-邻近条件下空间实体三维建模算法研究

倪 曙1，方源敏2，李国柱1，陈 杰2

(1.昆明市测绘研究院，云南昆明 650051；2.昆明理工大学国土资源工程学院，云南昆明 650093）

一、引 言

空间形体的三维建模算法是当前测绘制图和GIS领域研究的重点。传统的建模算法一般以平面作为定义域，实数空间的子集作为其值域，定义域与值域存在唯一的映射关系，由此产生的函数关系决定了传统建模算法的二维本质。函数是用数学术语来描述现实世界的主要工具。

传统的建模算法多以Delaunay三角网、Voronoi图(又称Thiessen多边形）为核心进行扩展，DEM就是其中的典型代表。不管是附加约束条件的DEM[1]，还是分段拼接来表达空间形体的建模算法，实际上都在函数的范围内。前者理论上可以通过一体化的函数来表示，后者则可以使用分段函数表示。而对于“悬崖”这样的地貌，前述算法则无能为力，因为在数学上已经跨出了函数的范畴。

针对空间离散点集进行三维建模的算法种类较多，包括雕刻家算法[2]、距离函数算法[3]、表面生长算法[4]和基于空间闭合投影面的建模算法[5-7]等。在点群密度不均匀或存在噪声的情况下，容易导致拓扑连接错误；而对于基于空间投影面的建模算法，在投影法线确定的前提下，存在多个点投影于同一点的问题等；通过以各点位投影中心进行切平面投影的算法[8]建模效率较高，但是无形中也会带来局部变形。

本文从理论出发，研究了一种三维建模算法。在逐点插入的过程中进行实时优化，同时采用有效的方法规避了由于K取值有限所导致的局部“孤立点群”的问题，同时对“同棱点”也作了有效的处理。结合具体应用，如针对地下采空区进行激光扫描获取的点云数据进行处理时，对点群进行逆向计算求定站心坐标作为本算法中的虚拟中心，建模结果能够最大化地逼近采空区的真实形态。

二、基本约定、研究对象及研究目标

研究对象及目标：给定空间离散点集

式中，Pi＝(xi，yi，zi），n≥4。当且仅当n≥4时，4点不共面，对其进行三维建模。

关于方向的确定，本文遵循右手法则。对于给定的三角形面片，对其法线方向使用右手准则，相对观察者而言，如果顶点以逆时针顺序排列时，则为该三角形面片的正面；反之则为背面。

如图1中的三棱锥P4―P1P2P3所示，对于面P1P2P3，v1为其外法线方向，按照右手准则，正面的顶点环绕顺序如图中箭头所示为P1→P2→P3→P1，背面的顶点序则为P3→P2→P1→P3。在本文中，面片的记法按照上述的表述进行(记法中隐含了该面片的法线方向）。

图1 右手法则

在给定三角形顶点的环绕顺序后，面片的外法线向量也随之被确定。以图1中的面片P1P2P3为例，对应的外法线向量v1可通过向量之间的叉积计算得到

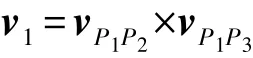
对于点集Pn的一种闭合三角构造，若内部存在一点P，使得P点到各三角面片中心的向量VD与各面片的外法线向量Vn的点积VD·Vn≥0(用于确定三角面片外法线的方向），且不相邻的三角面片不相交，则称该构造为针对点集Pn的一个简单空间构造，对应的实体模型为简单空间实体，点P称为该构造的核点。点P的集合称为对应于该构造的核。

三、基本数据结构的定义

根据建模算法的需要，定义一些基本的数据结构，主要包括点、边和面，见表1、表2、表3。

表1 点

点是基本的数据单位，其中，标志位用于标记该点的状态，包括未用、已用或是同棱点。

表2 边

表3 三角面片(外法线逆时针排序）

边是直接用来描述模型的基本结构之一。使用索引有一系列的优点，可以避免由于在建模过程中执行处理或后期空间分析时的浮点运算导致模型开裂等问题。

如图2所示，边P1P2左侧的三角形为P1P2P3，右侧的三角形为P1P4P2，左右侧的三角形拓扑信息使用相应三角形的索引编号进行设置，由此，边P1P2便成为内部边。对于边P1P4、P4P2、P2P3和P3P1，只有左侧三角形，左侧三角形的拓扑信息使用相应三角形的索引编号设置，右侧三角形的索引编号则设置为-1。边代表了实体模型构建过程中的一个侧面，如果两侧均处于使用状态，则该侧面位于内部；如果只有单侧处于使用状态，则为外部侧面。在构建模型的过程中，内部边/面将不再参与构建工作，算法拓扑推进的过程中只遍历外侧面。

图2 边的拓扑信息

面也是模型的基本拓扑结构之一。本文中涉及的面由三角形表示。对于顶点的索引，从顶点1→顶点2→顶点3，按照外法线右手法则确立；对于边信息，采用相应的边索引号填充。标志位记录了构成当前面片边的方向信息。如果构成当前三角形的边与边表中的边同向，则相应的bit置位；否则复位。

如图3所示，如果构成当前三角面片的1号边与边表中的边同向，则b0设置为1，反向则设置为 0；同理，如果2号边与边表中的边同向，则b1设置为1，反向则设置为 0；如果3号边与边表中的边同向，则b2设置为1，反向则设置为0。

最终建模算法中用到的主要数据容器包括主点集列表、K-邻接表、边表和面表。

图3 三角面片的标志位

四、三维构造算法

以空间点集Pn为对象，具体的三维构造算法如下：1）剔除同位点，并建立邻接表。设立阈值Epsilon，对于给定的两点P1和P2，如果两点间的距离

则视点P1和P2为同位点，将其中的一点从主点集中剔除。同时，在遍历点集的过程中，以每个点为邻接表的表头，计算出与其相邻的最近K个点，并记录在邻接表中，本文中选K＝8(经验值）。在构建邻接表的过程中，对每条记录内部的K个邻接点按照距离由小到大进行排序，对于全部的邻接表则依全部记录中每条记录的第1个邻接点的距离由小到大进行排序处理，所采用邻接表的形式见表4。

表4 邻接表的形式

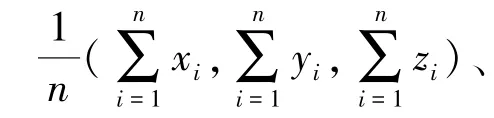
3）起始边及起始面片的确立。从邻接表中选取最短边作为起算边，并通过筛选该最短边的K临近点，按照最小角最大化的原则选择最优点建立起始三角面片。以点C为中心，构建初始三棱锥。使用公式VD·Vn≥0，确立三角面片的环绕方向。其中，VD为点C到三角面片中心的方向向量，Vn为自然顺序下求得的法线向量。如果两个向量的点积满足大于等于0的条件，则使用自然顺序；反之则将点位反序排列。创建面片变量，按计算确定的顺序填充对应的顶点信息域，并将其加入到面表中。

创建3个边变量，使用初始面片的信息填充变量的各个域，并将它们加入到边表中。按照边表中边的信息，填充面片中相应边的索引信息，将构成该起始面片的3个顶点设置为“已使用”的状态。

4）建立循环遍历邻接表。在遍历邻接表的时候遵循两个原则，在建模的过程中建立变量跟踪待插入点。优先从前插入点的K个近邻中选择点作为当前插入点；如果其近邻都已执行完插入操作，则顺次遍历邻接表，取下一个表头点作为当前点。这种处理能够有效地解决由于邻接表K取值的有限性所导致的局部点群“被孤立”的问题。

判断当前点与以C为中心的已有各表面片的位置关系。在本文中，边是有方向的。对于给定的点P，点P和边PiPj的位置关系可转换为向量VCP和面PiPjC的位置关系。计算PiPjC的外法线向量Vn，并计算点积VCP·Vn。设定阈值Epsilon2，如果VCP·Vn的绝对值小于Epsilon2，则认为点P位于边PiPj上；如果VCP·Vn＞Epsilon2，则点P位于边PiPj的左侧；反之，则位于右侧。

如果点P位于面表中某一面片3条边的左侧，计算向量VCP与当前面片外法线向量的点积，如果大于等于0，则该点位于三棱锥内部。如果点P位于某条边上，继续测试点P与起点的距离是否小于当前边的长度，如果小于则位于边上；反之则位于外部；如果点P既不在棱锥内部，又不在某条边上，则为外部点。待插入点与三棱锥构成如下3种位置关系。

a.矢量VCPi在三棱锥内部，如图4所示。

图4 当前点位于某三棱锥内部

b.矢量VCPi在三棱锥侧面上，如图5所示。

图5 当前点位于某棱锥的侧面上

由于边和面的拓扑信息是相关的，需做好新增面片和边的记录，以便于在插入完成后，更新相应的拓扑信息。

c.矢量VCPi在三棱锥的外侧，如图6所示。

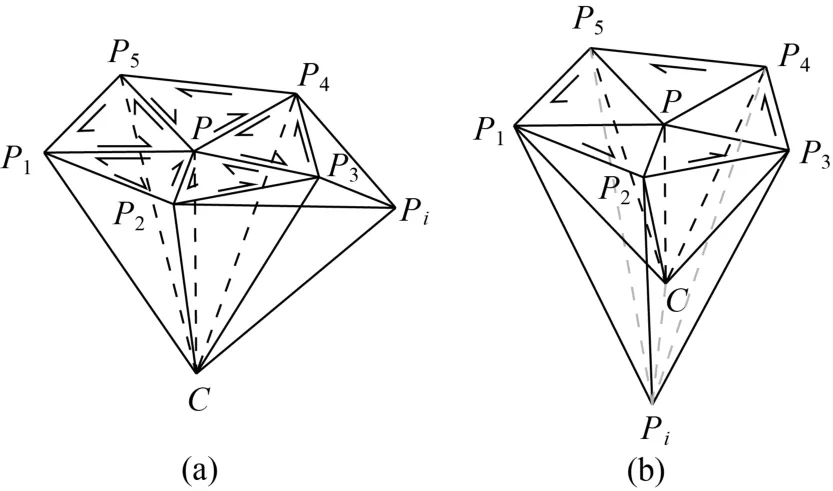
图6 当前点位于已有棱锥的外侧

如果当前点位于已建立棱锥的外侧，则进一步对其测试是否与已有棱锥的侧棱同棱，如果当前点与已有棱锥的某条棱同棱，则将其标记置为“同棱点”，等待后续处理；否则继续执行主建模流程。

如图6所示，点Pi位于已有棱锥的外侧，遍历边表，如果边表中当前边的两侧面片的拓扑信息都有效(不为-1）则跳过；如果只有一侧有效，则判断向量VCPi和该边的位置关系，在一条边只能被两个面片所共享的条件下，完成外侧边的插入操作。图6(a）中所示的VCPi只能看到部分棱锥，而图6(b）中的VCPi则能看到当前已有棱锥的全部外侧面。执行相应的插入操作，并更新面表和边表中相应的拓扑信息。

隐含说明：在经过上述位置判断后，如果直接执行插入操作，则最终的建模结果将会包含许多较深的“凹角”，数学上就是对应二面角的平面角过小所导致的。在执行插入操作的过程中，需在最小角最大化原则下，对新增面片执行拓扑优化。

5）将当前点的标志记为“已使用”的状态，循环直到K邻接表的表头点全部处于“已使用”或“同棱点”状态。

6）同棱点的处理。遍历主点集列表，将每个标记为同棱点的点插入到与其最近邻的点构成的面片中。其中包括了局部面片的打破和重建操作，以获取最佳拓扑连接。

五、试 验

使用C语言对本算法进行了实现，采用两套数据集进行了试验。数据集1是采用算法随机生成的空间球面上的500个点，数据集2是某大型金属矿山地下采空区的点云数据，其中有顶点23 939个。算法建模效果如图7、图8所示。

图7 球面随机采样点集的建模效果

图8 地下采空区点集的建模效果

六、结 论

本文从几何的角度出发，研究了一种三维建模算法。在没有考虑各点空间属性的情形下，将各点对虚拟中心向量的权重选择为1.0(即各点在数学上具有均等性）进行建模的工作。最终的模型由三角面片组成，建模的结果非常方便体积和表面积等的计算。本文的建模算法可作为空间大型复杂实体或一体化建模的基石。下一步的研究工作是：①对算法进行优化，以期能采用更优的复杂度来解决建模问题；②附加顶点属性的权重Ki的计算方法及其对最终模型的影响。

[1]陈学工，李源，曹建，等.Delaunay三角网剖分的约束边嵌入改进算法[J].计算机工程与应用，2009，45(24）：235-237.

[2]EDELSBRUNNER H，MUCKE E P.Three-dimensional Alpha Shapes[J].ACM Transactions on Graphics，1994，13(1）：43-72.

[3]HOPPE H，DEROSE T.Surface Reconstruction from Unorganized Points[J].Computer Graphics，1992，26(2）：71-78.

[4]LIN H，TAI C L，WANG G.A Mesh Reconstruction Algorithm Driven by Intrinsic Property of Point Cloud[J]. Computer-Aided Design，2004，36(1）：1-9.

[5]张帆，黄先锋，李德仁.基于球面投影的单站地面激光扫描点云构网方法[J].测绘学报，2009，38(1）：48-54.

[6]郑德华，庞逸群，曹操.基于椭球面投影的散乱点云建立三角格网方法[J].测绘工程，2010，19(4）：19-23. [7]郑德华，张云涛.基于物体表面散乱三维激光扫描点的三角形格网建立[J].测绘工程，2004，13(4）：62-65.

[8]郑顺义，苏国中，张祖勋.3维点集的自动表面重构算法[J].武汉大学学报：信息科学版，2005，30(2）：154-157.

A Method of Three-dimensional Modeling over Spatial Unorganized Points Based on the K-nearest Neighbours

NI Shu，FANG Yuanmin，LI Guozhu，CHEN Jie

以空间离散点集Pn＝{P1，P2，…，Pi，…，Pn}为研究对象，研究了一种三维建模算法。在预先约定外法线方向和优化原则(最小角最大化）的基础上进行三维建模。第1步，对点集进行同位点的剔除，并建立K-邻近邻接表；第2步，确定权重的计算方法，并计算虚拟中心点、各点相对于虚拟中心的向量及其长度范数；第3步，求定起始边及起始面片；第4步，遍历K-邻接表，选择当前待插入点，分3种情况讨论了待插入点与已有面表中面片和已有边表中边的关系，进行插入和格网优化操作，直到主点集中的点都处于“已使用”或“同棱点”的状态；第5步，处理“同棱点”。通过上述环节完成对空间离散点集的三维建模操作，最后用C语言对算法进行了实现，并采用相关的数据进行了试验，试验结果证明了本算法的有效性。

空间离散点集；三维建模；空间实体；K-邻近；地下采空区

P208

B

0494-0911(2014）10-0036-05

2013-09-09

国家自然科学基金(41161071）；昆明理工大学自然科学研究基金(KKSY201321063）

倪 曙(1969―），男，云南宾川人，高级工程师，主要研究方向为三维GIS、工程测量及大地测量。

倪曙，方源敏，李国柱，等.K-邻近条件下空间实体三维建模算法研究[J].测绘通报，2014(10）：36-40.

10.13474/j.cnki.11-2246. 2014.0323