基于多点的区域性椭球确定

吕志鹏，伍吉仓，2

(1.同济大学测绘与地理信息学院，上海 200092；2.现代工程测量国家测绘地理信息局重点实验室，上海 200092）

基于多点的区域性椭球确定

吕志鹏1，伍吉仓1，2

(1.同济大学测绘与地理信息学院，上海 200092；2.现代工程测量国家测绘地理信息局重点实验室，上海 200092）

一、引 言

为了限制长度综合变形，我国多数城市控制网及工程控制网均采用独立坐标系，一般是构造一个与测区平均高程面或似大地水准面非常接近的区域性椭球面作为边长的归算面和坐标的投影面。这样可以保证在测区范围内实测的边长和坐标反算得到的边长满足限差要求(城市测量规范中要求长度综合变形不大于2.5cm/km）。对于测区范围比较大的情况，可以进一步选取过测区中央的子午线作为高斯投影中央子午线的方法限制边长变形。在独立坐标系建立过程中，椭球变换是核心环节。椭球变换的方法分为单点法[1-6]和多点法[7]。单点法本质上是使区域性椭球面与投影面(测区平均高程面或似大地水准面）在基准点处充分接近。在平均高程h0＝1000 m，测区面积为10 000 km2的情况下，单点法能保证测区边缘处投影面与区域性椭球面的差异优于2～3 m[3]。然而这一结论并没有考虑高程异常误差，以及投影面与参考椭球面之间的倾斜和不同程度起伏的影响。随着GPS技术广泛应用于城市控制网的建立与改造，以及各种工程控制网的布设，投影面相对于参考椭球面的差距可以精确求得。故投影面与参考椭球面之间的倾斜和不同程度的起伏成为建立独立坐标系的主要影响因素。为此，文献[7]提出利用测区内的多个点确定区域性椭球的方法，取得了良好的结果。本文基于多点法提出了一种新的区域性椭球构造方法。

二、基于多点的区域性椭球确定原理

1.基于位置基准点的椭球中心平移

独立坐标系建立于一般基于国家参考椭球，在其基础上进行椭球参数的改变、椭球的重新定位定向及尺度的变化，以满足区域性椭球面与投影面在测区范围内最佳密合的条件。单点法建立独立坐标系基于一点进行椭球变换，即在位置基准点处保证区域性椭球面与投影面充分接近。如图1所示，点P0为建立独立坐标系的位置基准点(通常为测区中点），其所对应的大地高为H0，正常高为h0。H0′是点P0相对于区域性椭球面的大地高。设位置基准点P0处的高程异常为ζ，则该点处投影面相对于参考椭球面的垂直距离ΔH0＝Δh＋ζ＝H0-(h0-Δh），其中Δh为投影面的正常高。将参考椭球面沿位置基准点P0的法线方向平移ΔH0，且不改变椭球的长半径和偏心率，则椭球中心的平移量为

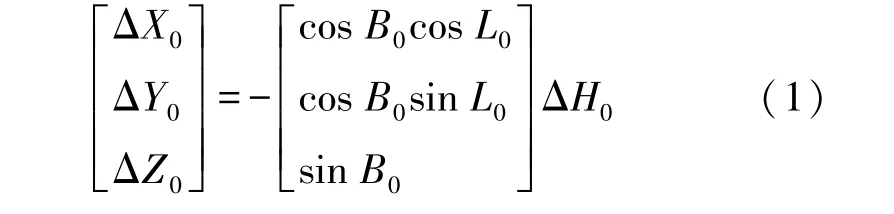
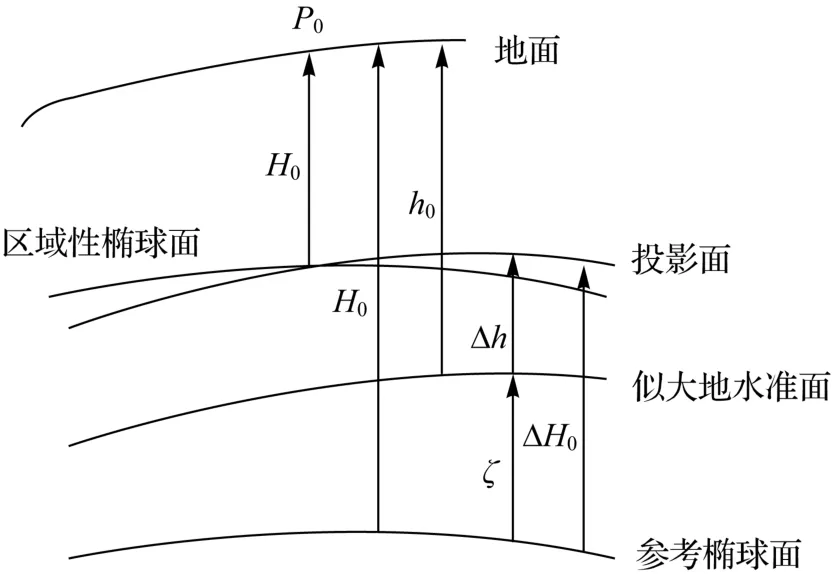
图1 单点法独立坐标系建立示意图

各点大地坐标的变化为

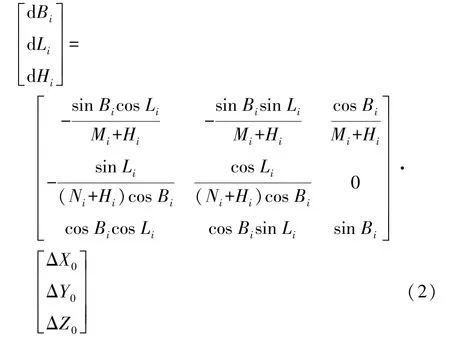
2.基于多点定向的区域性椭球确定

单点法不能对椭球进行重新定向以调整区域性椭球面相对于投影面的倾斜，同时单点法也无法顾及测区的起伏对区域性椭球面确定的影响。为此有必要根据测区内的多个点进行椭球的重新定向。在位置基准点P0上建立站心地平坐标系，它的法线方向为z轴，向外为正。x轴指向点P0处大地子午线方向，向北为正。y轴垂直于xP0z，向东为正。如图2所示。在位置基准点P0处法线方向与垂线方向并不一致，其夹角即为垂线偏差，它可以分解成子午分量ξ和卯酉分量η。故在站心地平坐标系中以P0为旋转中心，先绕y轴旋转ξ，再绕x轴旋转-η (对于左手坐标系，旋转角以顺时针为正），就可以消除平均高程面相对于椭球面的倾斜。根据站心赤道坐标系和站心地平坐标系之间的转换关系可得[8]

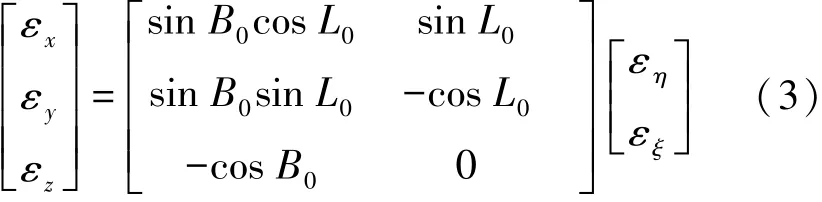
式中，εη＝-η；εξ＝ξ；εx、εy、εz为站心赤道坐标系下的旋转角。

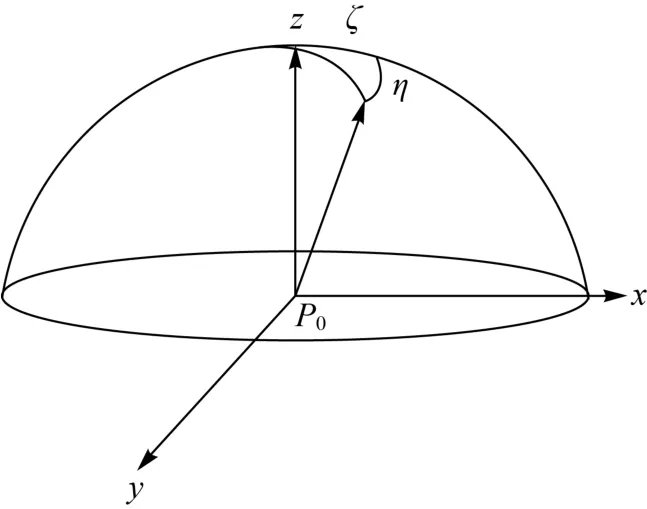
图2 站心坐标变换示意图

位置基准点P0作为站心坐标系的原点，即为旋转变换的中心，有必要使其在旋转变换前后保持不变。为此应用只顾及旋转变换的莫洛金斯基转换模型，如下

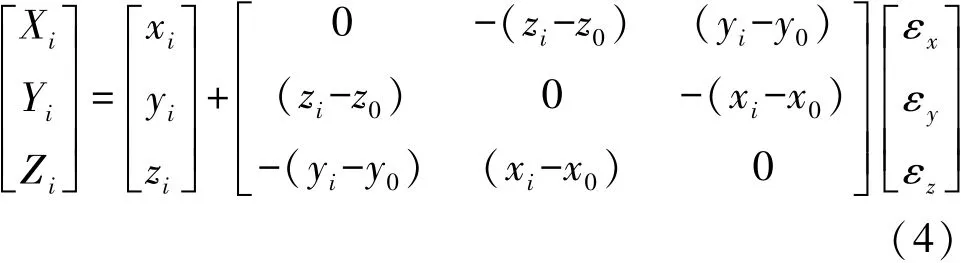
式中，(xi，yi，zi）为旋转变换前的椭球对应的三维空间直角坐标；(x0，y0，z0）为相应的位置基准点P0的坐标；(Xi，Yi，Zi）为旋转变换后的椭球对应的三维空间直角坐标。由于旋转变换前后各点的坐标变化量级微小，故根据大地坐标微分方程有

式中，下标为0的参数为位置基准点P0所对应的参数。

设测区的平均高程面为Δh，任意一点处的正常高为hi，大地高为Hi，则可求得该点处椭球面和投影面的垂距为将式(6）写成误差方程形式

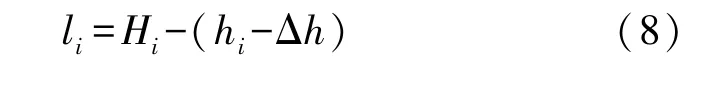
其中

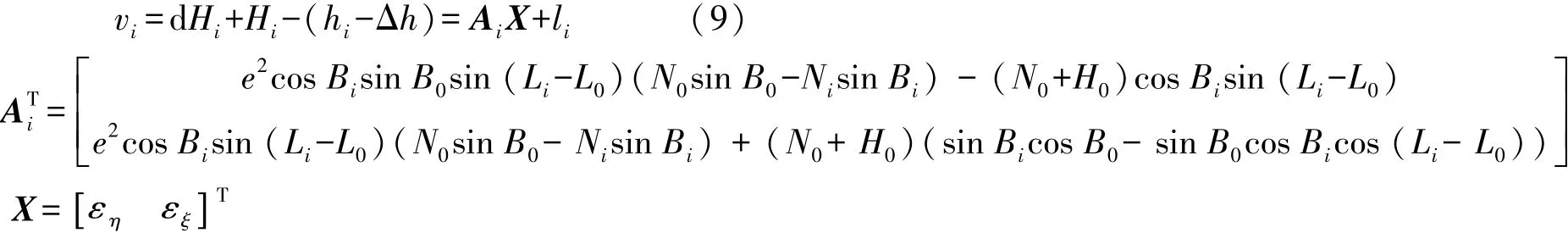
根据测区内均匀分布的多点按最小二乘法可得

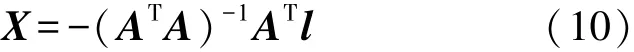
3.多点确定区域性椭球的必要性分析

在进行控制网布设时，应将边长观测值进行高程归化，其公式如下

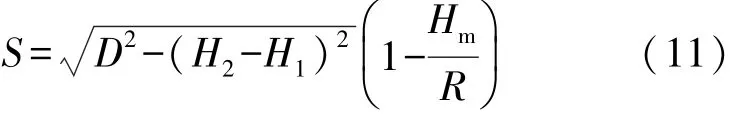
式中，S为测距边所对应的投影面弧长；D为测距边的倾斜距离；Hm为测距边两端点的平均大地高；H2、H1分别为测距边两端点的大地高。在城市控制网及工程控制网布设过程中，由于投影面通常选取为某一水准面(测区平均水准面或似大地水准面），因而，上述大地高可以用正常高来代替。为此需要进行椭球变换，使得各点处的正常高与其所对应的区域性椭球面的大地高相一致，以消除边长观测值的高程归化误差。将式(11）两端对高差求导得

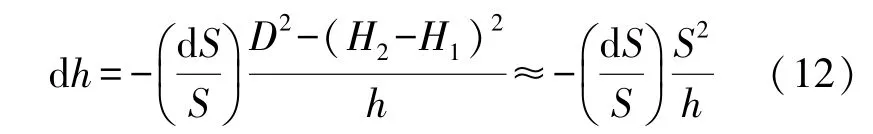
式中，h＝H2-H1。当S＝10 000 m，(dS/S）≤10-6，h＝1000 m、500 m、200 m、100 m、10 m时，高差精度限差见表1。

表1 高程测量精度m

由表1可知，对于相同长度的测距边随其两端点高差的增大，为了保证长度归算的精度，高程精度也相应地提高。高差精度由两部分组成：水准测量精度和投影面与区域椭球面的倾斜误差。对于单点法确定的区域性椭球，在面积为10 000 km2的测区边缘处投影面与区域椭球面会产生3 m左右的倾斜误差。假设倾斜误差以位置基准点为中心，沿径向均匀变化，故其变化率为0.6 m/10 km。因而，当测距边两端点高差变化较大时，投影面与区域椭球面不一致所造成的误差影响显著，有必要确定与投影面更加一致的区域性椭球面。

三、计算实例

某C级GPS控制网点位分布如图3所示，由14个点组成，依次标记为P1―P14，在图中用三角形表示GPS点位。测区东西长度约为200 km，南北长度约为50 km，实际控制面积在10000 km2左右。在各GPS控制网点联测水准获得各点的正常高。选取大致位于测区中心的P1点作为旋转中心，采用似大地水准面作为投影面。应用本文的算法确定区域性椭球，区域性椭球上的大地高及其与正常高之间的差异见表2(图中格网间距为30″）。

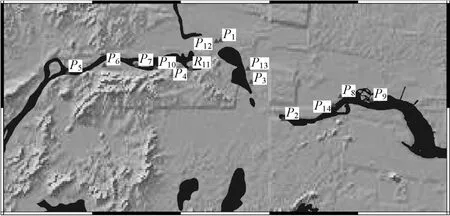
图3 GPS点位分布图

表2中大地高1和偏差1为采用全部GPS点进行区域性椭球确定得到的各点相对区域性椭球的大地高及其与正常高的偏差。利用本文算法进行区域性椭球确定，由于基本消除了旋转中心处的垂线偏差的影响，所得区域性椭球面与作为投影面的似大地水准面的密合程度良好，在所有GPS控制点上两者的差异均小于10 mm，考虑到测量误差的存在，实际上区域性椭球面和似大地水准面在测区范围内具有一致性。同时，由于将区域性椭球面与似大地水准面之间的差距在测区范围内控制在10 mm之内，因而可以根据GPS定位结果经上述椭球变换过程直接获得精度优于10 mm的正常高(不考虑GPS测量误差的影响）。

接下来选取测区内均匀分布的点P1、P2、P5、P7、P9、P11、P13、P14进行区域性椭球的拟合，用其他点检核拟合质量，得到的各点相对区域性椭球的大地高及其与正常高的偏差分别为大地高2和偏差2。仅利用测区内均匀分布的8个点进行区域性椭球拟合相对于按全部点进行拟合，拟合偏差的最大值和均值均未发生显著变化，并且处于测量噪声的水平，对区域性椭球的确定不会产生影响，说明本文算法的外附合精度良好。

同时，对测区边缘处点P5、P2、P9的经纬度变化进行计算，结果见表3。

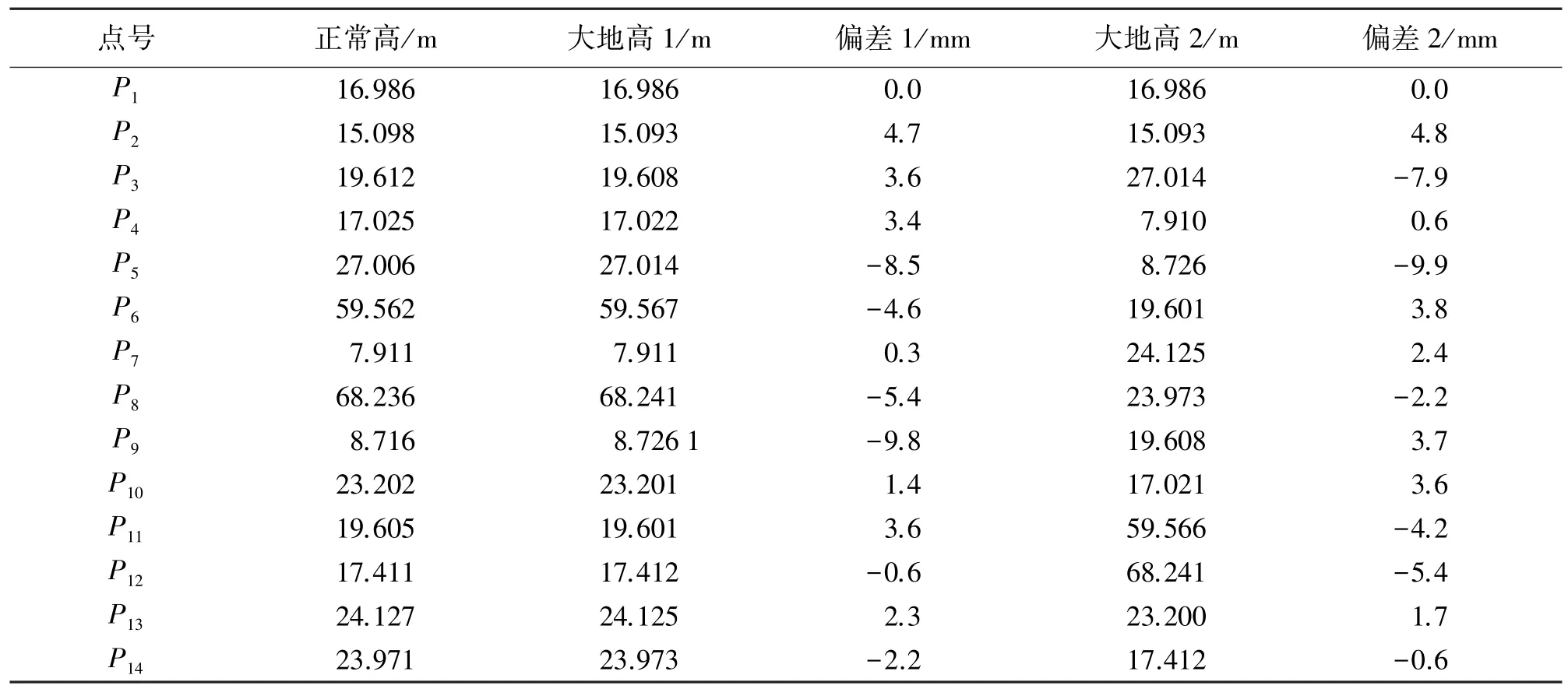
表2 调整后的大地高及其与正常高的差异

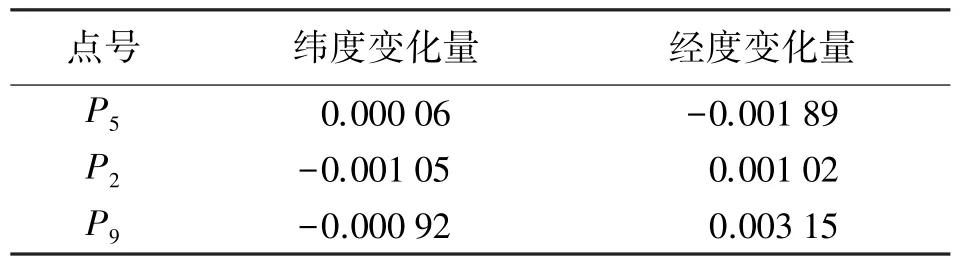
表3 测区边缘处点位经纬度变化(″）

由表3可知，在整个测区范围内，经纬度变化的量级均小于10-3(″）。这一方面可以保证各微分关系式的成立；另一方面对于实际的工程应用，可以不顾及由于椭球变换造成的经纬度的变化直接进行高斯投影变换。

为了与其他算法进行比较，利用文献[1]、[2]、[7]中的算法分别根据上述计算实例确定区域性椭球，各种算法的拟合偏差绘制于图4。

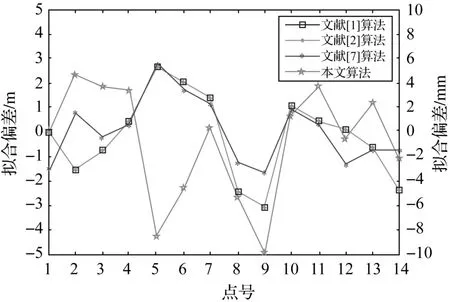
图4 不同算法比较

文献[1]、[2]、[7]中算法的拟合偏差较大，用左侧的纵坐标轴标注，本文算法的拟合偏差较小，用右侧的纵坐标轴标注。文献[1]通过将参考椭球沿位置基准点的法线方向平移使得在该点处构造的区域椭球面E2和投影面相切。由图4可知，这种方法在测区边缘点P5、P9处产生3 m左右的偏差。文献[2]通过改变参考椭球长半径和偏心率并且保证在位置基准点处法线方向不变的方法构造区域性椭球E3，使得在该点处区域性椭球面与投影面相切，其拟合偏差图像与文献[1]重合。单点法由于难以消除区域性椭球面相对于投影面的倾斜，造成在测区边缘处两面的较大偏差。文献[7]是在文献[3]所构造的E3椭球的基础上，通过确定各点相对于E3椭球的大地高，并利用多点计算与投影面最佳密合的区域性椭球参数，相对于文献[1―2]算法拟合偏差有所下降。本文算法首先利用文献[1]算法构造了E2椭球，然后在其基础上以位置基准点为中心进行旋转，最终获得各点的拟合偏差均小于10 mm。由于消除了区域性椭球面和投影面的倾斜误差，拟合偏差相对于单点法和文献[7]中算法有了很大的提高。

四、结束语

利用本文提出的算法，确定的区域性椭球面与投影面在整个测区范围内的密合程度相对于已有算法有了较大改进。这有利于将GPS控制网归算到已有地面基准，减小由于上述两面的不一致造成的GPS控制网尺度误差和坐标误差。同时，可以根据GPS定位结果经上述椭球变换过程直接获得厘米级精度的正常高(不考虑GPS定位误差影响），这对于实际工程应用很有裨益。相对于单点法区域性椭球确定而言，多点法显著地提高了区域性椭球面与投影面之间的密合程度。同时，多点法相对于单点法的计算模型更加复杂。因此，建议当测区范围较小时，考虑到单点法计算模型相对简单并且已满足归算精度的要求，宜采用单点法确定区域性椭球面；当测区范围变大时，利用一点确定的区域性椭球与投影面密合程度不佳的缺点就会显著影响边长的归算精度，造成长度综合变形超限，此时，应该运用多点法确定区域性椭球。

[1]李毓麟.GPS定位技术在城市测量中的应用[J].测绘通报，1993(2）：10-15.

[2]施一民.以城市控制网的基准数据归算GPS网的一种新方法[J].工程勘察，1993(6）：41-45.

[3]施一民.适合于独立网的区域性椭球的确定方法及论证[J].解放军测绘学院学报，1994(2）：88-93.

[4]丁士俊，畅开蛳，高琐义.独立网椭球变换与坐标转换的研究[J].测绘通报，2008(8）：4-6.

[5]李世安，刘经南，施闯.应用GPS建立区域独立坐标中椭球变换的研究[J].武汉大学学报：信息科学版，2005，30(10）：889-891.

[6]陆鹏程，李全海，朱丹.铁路独立坐标系的建立及坐标转换[J].测绘科学，2012，37(10）：20-22.

[7]施一民，张文卿.区域性椭球元素的最佳确定[J].测绘工程，2000，9(3）：27-29.

[8]张镇，黄宝安，黄夏琴.论城市平面控制网坐标系统投影带与投影面的选择[J].测绘学报，1982，11(1）：51-57.

[9]施一民.现代大地控制测量[M].北京：测绘出版社，2003.

[10]魏子卿.我国大地坐标系的换代问题[J].武汉大学学报：信息科学版，2003，28(2）：138-143.

[11]施一民.单点和多点法确定区域性椭球空间位置及元素[J].同济大学学报，2004，32(5）：648-651.

Determining Regional Ellipsoid Based on Multi-point

LV Zhipeng，WU Jicang

为了限制面积较大测区(＞10000 km2）的长度综合变形，提出一种区域性椭球面的构造方法。首先，将参考椭球沿位置基准点法线方向平移，使区域性椭球面和投影面在该点处重合；然后，以位置基准点为旋转中心进行旋转，消除区域性椭球面和投影面的倾斜误差。实测算例表明，各点相对于区域性椭球面的大地高和正常高的偏差达到厘米级精度，说明本文算法具有一定的实用价值。

区域性椭球；投影面；多点法；椭球平移；旋转

P282

B

0494-0911(2014）10-0011-04

2013-08-06

国家科技部国际科技合作重点项目(2010DFB20190）；国家自然科学基金(41074019）

吕志鹏(1988―），男，内蒙古赤峰人，硕士生，主要研究方向为地壳形变与地球动力学。

吕志鹏，伍吉仓.基于多点的区域性椭球确定[J].测绘通报，2014(10）：11-14.

10.13474/j.cnki.11-2246.2014.0317