利用单个地面控制点的SAR图像高精度立体定位

张红敏 靳国旺 徐 青 李向英

①(信息工程大学 郑州 450001)

②(中国测绘科学研究院 北京 100039)

③(61512部队 北京 100088)

利用单个地面控制点的SAR图像高精度立体定位

张红敏*①靳国旺①②徐 青①李向英③

①(信息工程大学 郑州 450001)

②(中国测绘科学研究院 北京 100039)

③(61512部队 北京 100088)

几何构像模型和定向参数解算方案的选择是实现SAR图像高精度立体定位的关键。该文针对稀少控制下斜侧视SAR图像高精度定位难题，设计了利用单个地面控制点的SAR图像立体定位方案。该方案利用轨道参数获取成像瞬间天线相位中心的位置、速度，并利用一个地面控制点标定近距延迟和多普勒中心频率，实现定向参数的精确解算和SAR图像的高精度立体定位。采用中国测绘科学研究院获取的机载SAR图像进行了立体定位实验，统计分析了其定位误差，验证了该文方法的精确性和有效性。

合成孔径雷达(SAR)；立体；定位；距离-多普勒；地面控制点(GCP)

1 引言

合成孔径雷达(Synthetic Aperture Radar, SAR)具有全天时、全天候等优点，是高分辨率对地观测的重要工具，尤其在多云雾、多雨雪地区地形测绘、应急测绘保障、境外目标定位等任务中存在巨大应用潜力[1－3]。利用SAR图像进行立体定位是测定地面目标位置信息的重要手段。

在SAR图像立体定位中，几何构像模型和定向参数解算方法的选择是实现高精度定位的关键。在几何构像模型选择方面，经典SAR构像模型包括距离-多普勒(R-D)模型[4]，F. Leberl构像模型[5](即正侧视R-D模型)，G. Konecny投影公式[6]，有理函数模型等；除上述模型外，学者们研究了SAR图像的有理多项式(Rational Polynomial Coefficient, RPC)模型[7]、距离-共面(Range-Coplanarity)模型[8]等。其中，R-D模型作为符合SAR图像成像机理的经典构像模型，应用较多，但已有研究大多将R-D模型的多普勒中心频率假定为零，即采用正侧视R-D模型进行SAR图像的定位处理[9－12]，在进行斜侧视SAR图像的立体定位时误差较大[13]。

定向参数解算通常依赖一定数量的地面控制点，缺少地面控制点情况下，定向参数一般由SAR系统参数和轨道参数获取[14]，然而由于上述参数误差的存在，常导致无控制定位精度较差[15]。为了实现稀少控制的立体SAR图像高精度定位，本文设计了利用单个地面控制点(Ground Control Point, GCP)的SAR图像斜侧视立体定位方案，利用轨道参数获取成像瞬间天线相位中心的位置、速度，并利用 1个地面控制点精确标定近距延迟和多普勒中心频率，实现斜侧视SAR图像的高精度立体定位。采用中国测绘科学研究院获取的机载 SAR图像进行了立体定位实验，验证了该方案的精确性和有效性。

2 利用单个控制点的SAR图像斜侧视高精度立体定位

为了提高稀少控制下SAR图像立体定位精度，本文设计了如图1所示的SAR图像高精度立体定位方案，在由轨道参数获取各天线相位中心位置、速度的基础上，利用1个地面控制点标定各图像的近距延迟和多普勒中心频率，从而由同名像点坐标精确交会计算出相应地面点的3维坐标。其关键步骤包括：

(1) 利用单个控制点的斜侧视R-D模型定向参数标定

在由轨道参数获取天线相位中心位置、速度的基础上，根据R-D模型，可由1个或1个以上的地面控制点标定近距延迟和多普勒中心频率。其中，R-D模型的表达式为：

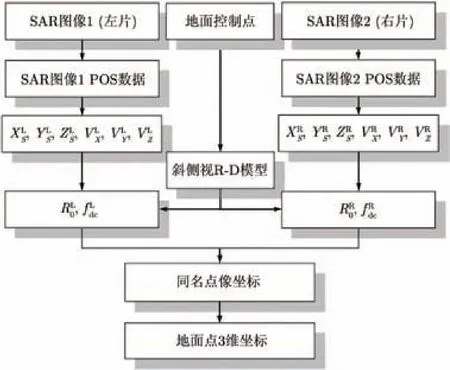
图1 利用单个地面控制点的SAR图像斜侧视高精度立体定位流程Fig. 1 Flow of accurate squint positioning of stereo SAR images with one GCP

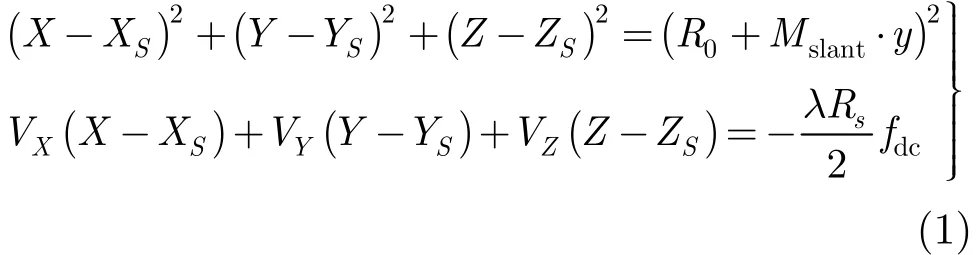
R-D模型根据成像时的距离条件和多普勒频移条件建立SAR成像瞬间相对严格的物像关系，符合SAR成像机理。考虑到R-D模型是关于近距延迟R0和多普勒中心频率fdc的非线性方程，本文采用线性化牛顿迭代答解的方法。

(2) 地面点3维坐标计算

由于式(2)是关于地面点3维坐标的非线性方程组，解算时采用线性化迭代答解方法。从而计算得到地面点3维坐标，完成相应同名像点的斜侧视立体定位。

3 SAR图像立体定位实验

采用中国测绘科学研究院获取的两个 SAR立体像对进行了稀少控制下的 SAR图像立体定位实验，SAR系统采用X波段，中心侧视角为48°, SAR立体像对的相关参数如表1所示。

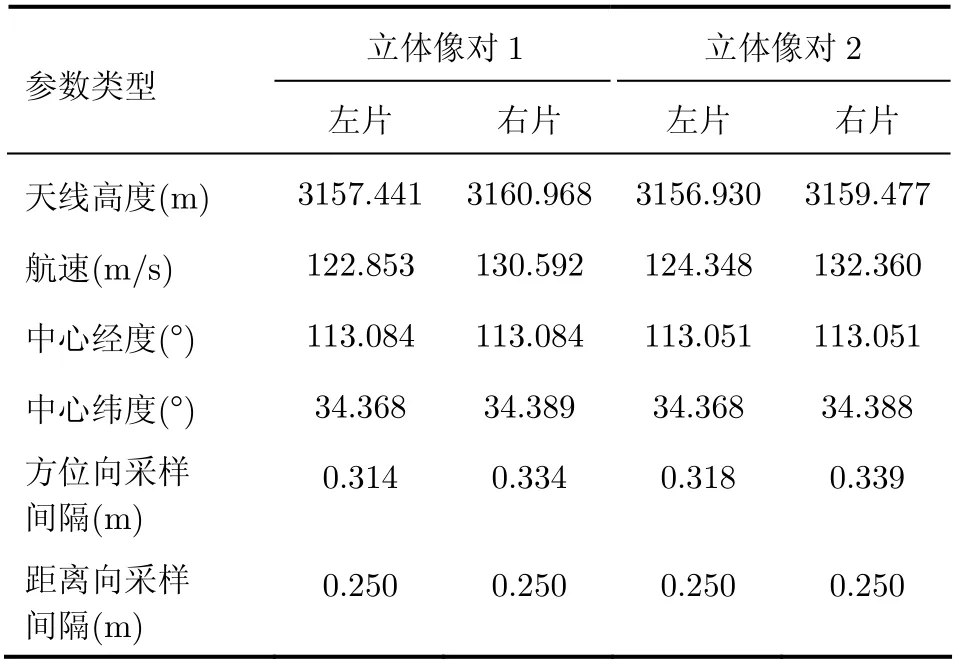
表1 立体SAR像对相关参数Tab. 1 Parameters of stereo SAR images

SAR立体像对1的控制点分布如图2所示，检查点分布如图3所示；SAR立体像对2的控制点分布如图4所示，检查点分布如图5所示；SAR立体像对 1，像对 2的控制点和检查点坐标分别如表 2和表3所示；为了控制数据的保密，将绝对坐标中的低位数值保留，高位数值以“***”代替。

现有的 SAR图像立体定位方法多利用多个控制点标定全部定向参数，为了充分验证本文方法的优势，对比实验中分别采用正侧视R-D模型和斜侧视R-D模型；采用正侧视R-D模型时利用3个或3个以上地面控制点标定天线相位中心3个位置分量和3个速度分量共6个定向参数，进而完成SAR图像的正侧视立体定位；采用斜侧视R-D模型时，由于近距延迟与天线相位中心位置、速度等参数相关，因此在对比实验中利用4个或4个以上地面控制点标定天线相位中心位置分量、速度分量和多普勒中心频率，共7个定向参数，进而实现SAR图像的斜侧视立体定位。

图2 SAR立体像对1控制点分布Fig. 2 GCP in stereo SAR images 1

图3 SAR立体像对1检查点分布Fig. 3 Check points in stereo SAR images 1

图4 SAR立体像对2控制点分布Fig. 4 GCP in stereo SAR images 2

图5 SAR立体像对2检查点分布Fig.5 Check points in stereo SAR images 2

表2 立体SAR像对1控制点和检查点坐标Tab. 2 Coordinates of GCP and check points in stereo SAR images 1

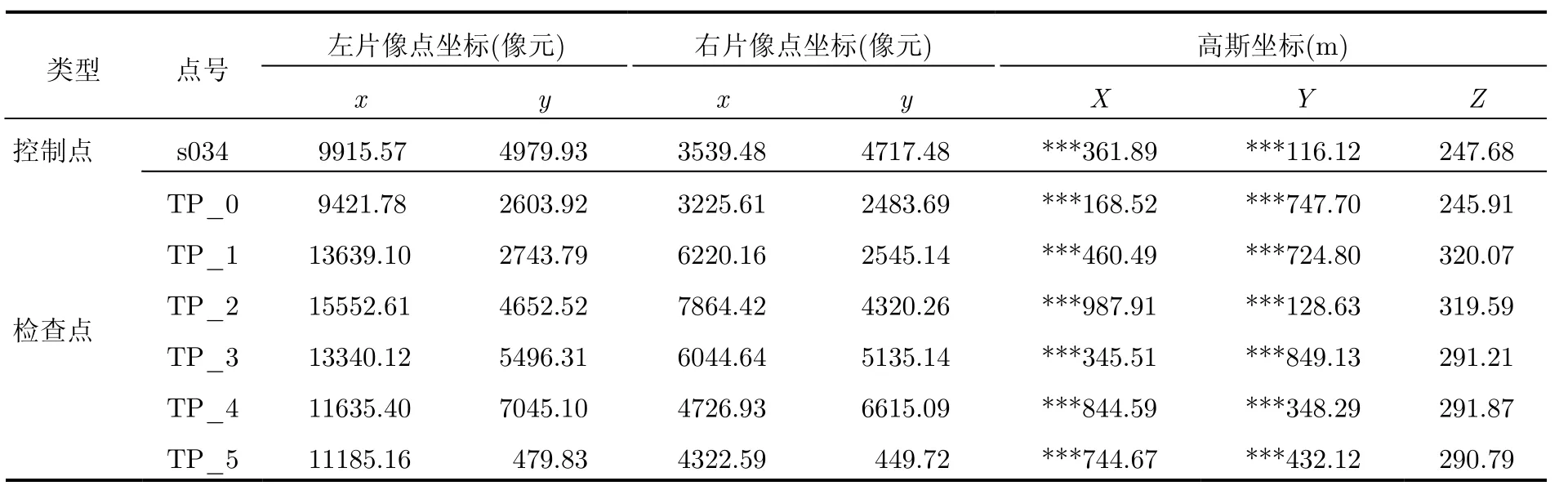
表3 SAR立体像对2控制点和检查点坐标Tab. 3 Coordinates of GCP and check points in stereo SAR images 2

采用上述多个控制点的正侧视立体定位方法、多个控制点的斜侧视立体定位方法和本文提出的单个控制点的斜侧视立体定位方法分别对立体像对 1和立体像对2进行了斜侧视立体定位，误差统计分别如表4和表5所示；采用本文方法的平面定位精度和高程定位精度如表6所示；标定前后的近距延迟和多普勒中心频率如表7所示。

由表4和表5可知，对于SAR立体像对1和SAR立体像对2，采用多个控制点的正侧视立体定位方法，检查点坐标误差最大；采用多个控制点的斜侧视立体定位方法，检查点坐标误差居中；采用本文提出的单个地面控制点的斜侧视立体定位方法，检查点坐标误差最小，约为 1 m。并且由表 6可知，采用本文方法，两个立体像对的平面定位精度和高程定位精度均为1 m量级。分析其原因在于：

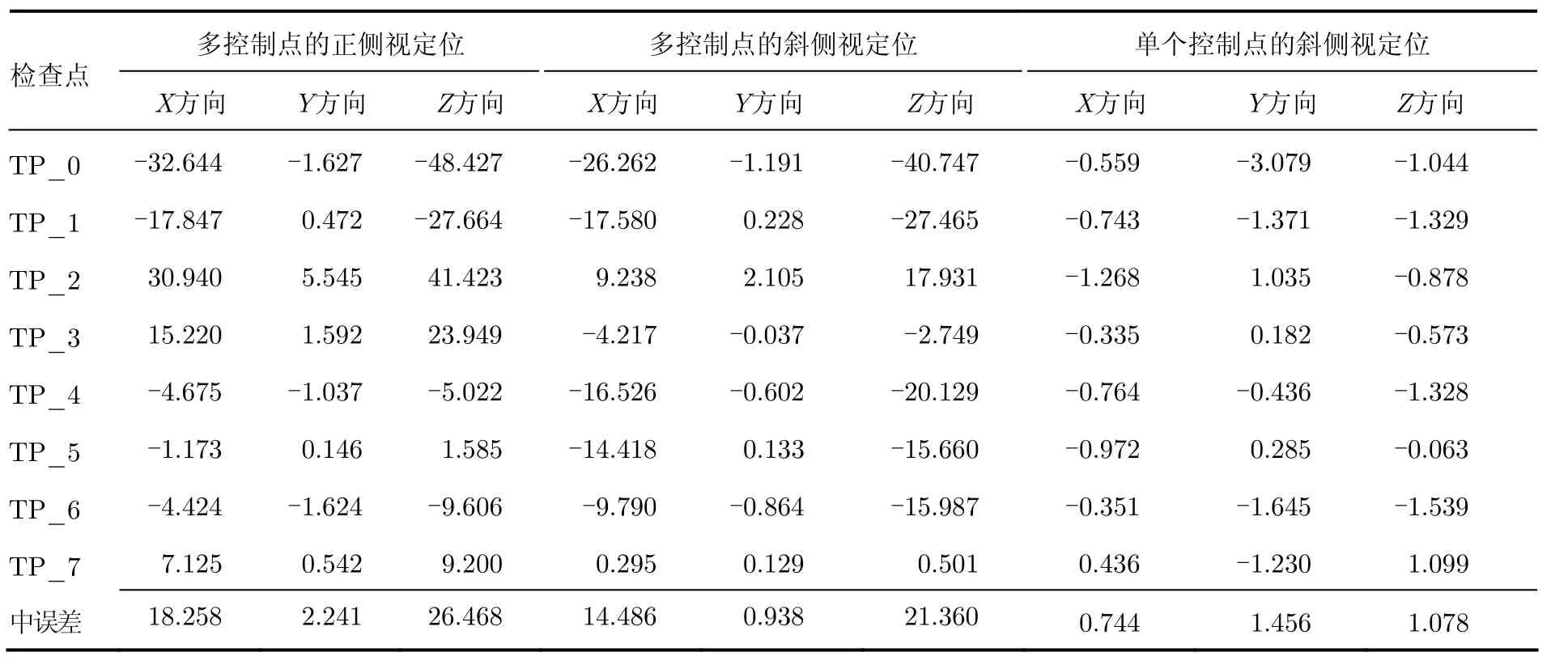
表4 SAR立体像对1斜侧视定位误差统计(m)Tab. 4 Squint positioning errors of stereo SAR images 1 (m)

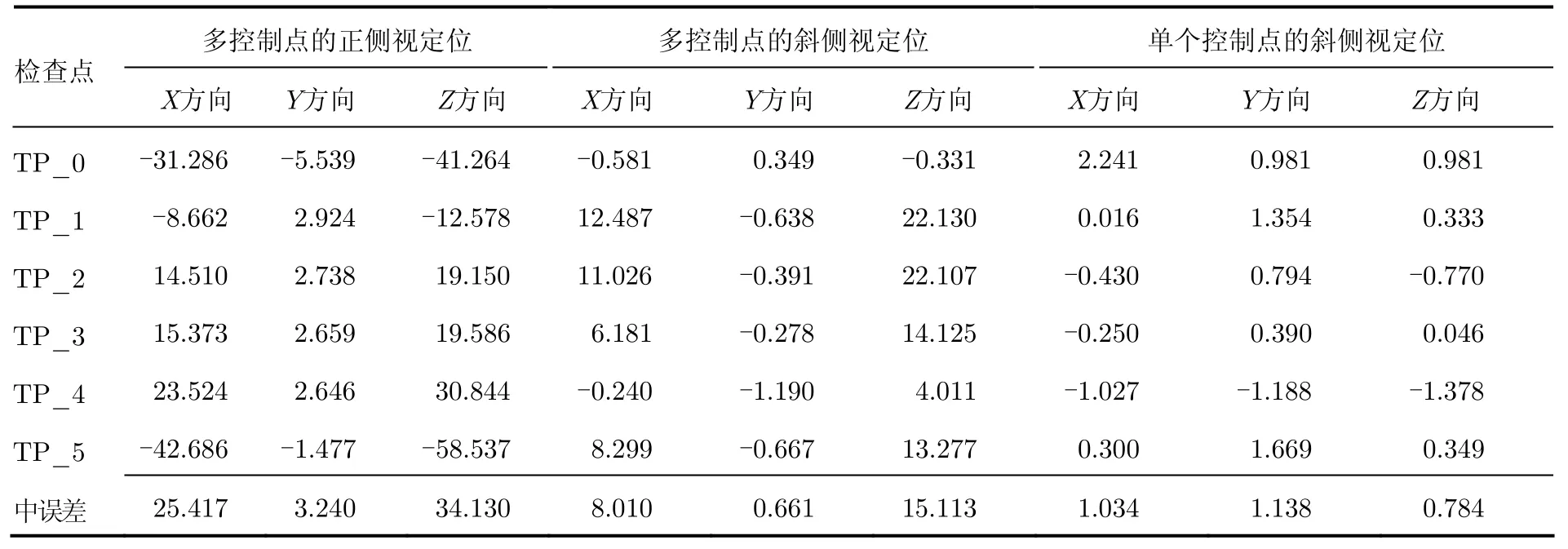
表5 SAR立体像对2斜侧视定位误差统计(m)Tab. 5 Squint positioning errors of stereo SAR images 2 (m)

表6 利用单个地面控制点的SAR立体定位平面及高程精度统计(m)Tab. 6 Plane precision and elevation precision of positioning with stereo SAR images and one GCP (m)

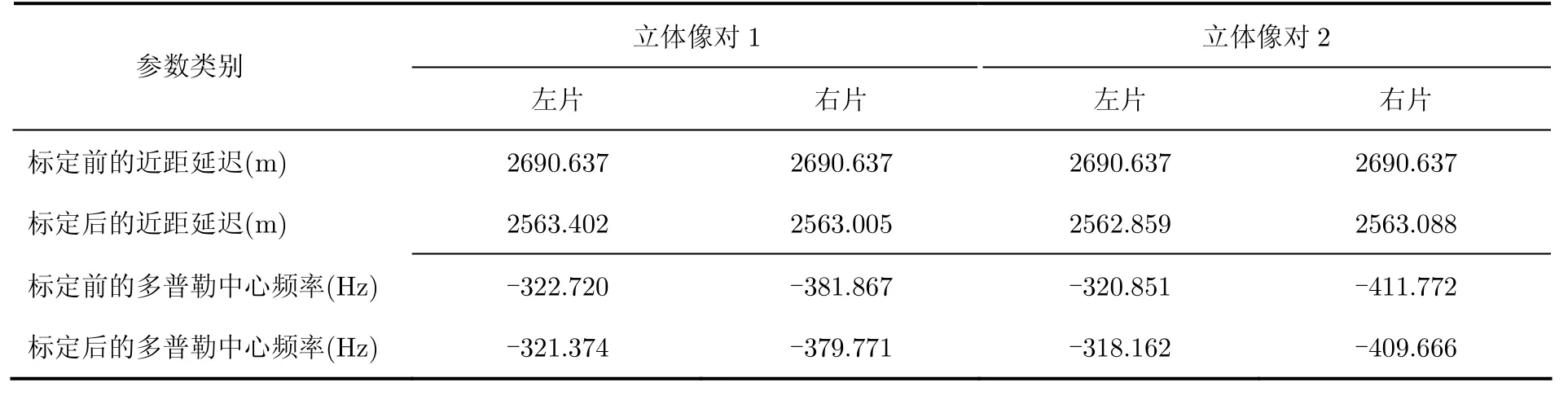
表7 标定前后的近距延迟和多普勒中心频率Tab. 7 The close range and the Doppler centroid before and after compensation

(1) 采用正侧视 R-D模型不符合机载斜侧视SAR图像构像机理，因此利用其进行立体定位，定位误差较大；为了提高斜侧视SAR图像定位精度，应采用斜侧视R-D模型；

(2) 由于近距延迟与天线相位中心位置、速度等参数相关，现有的斜侧视立体定位方法难以利用控制点同时标定全部定向参数，因此近距延迟通常采用系统参数提供，然而该系统参数存在一定误差，导致现有斜侧视定位方法误差较大；

(3) 本文方法利用了精度较高的POS数据获取天线相位中心位置、速度等参数，利用1个地面控制点标定近距迟延和多普勒中心频率，较好地修正了上述参数的误差(如表 7所示)，因此可实现高精度的SAR图像立体定位；

(4) 本文方法充分利用了轨道参数等已有信息，只需一个地面控制点即可实现1 m量级的立体定位，较好地降低了对地面控制点数量和分布的要求。

为了充分验证本文结果的正确性与可靠性，分别计算了上述两组数据各检查点对应的系数矩阵条件数，分别如表8和表9所示。

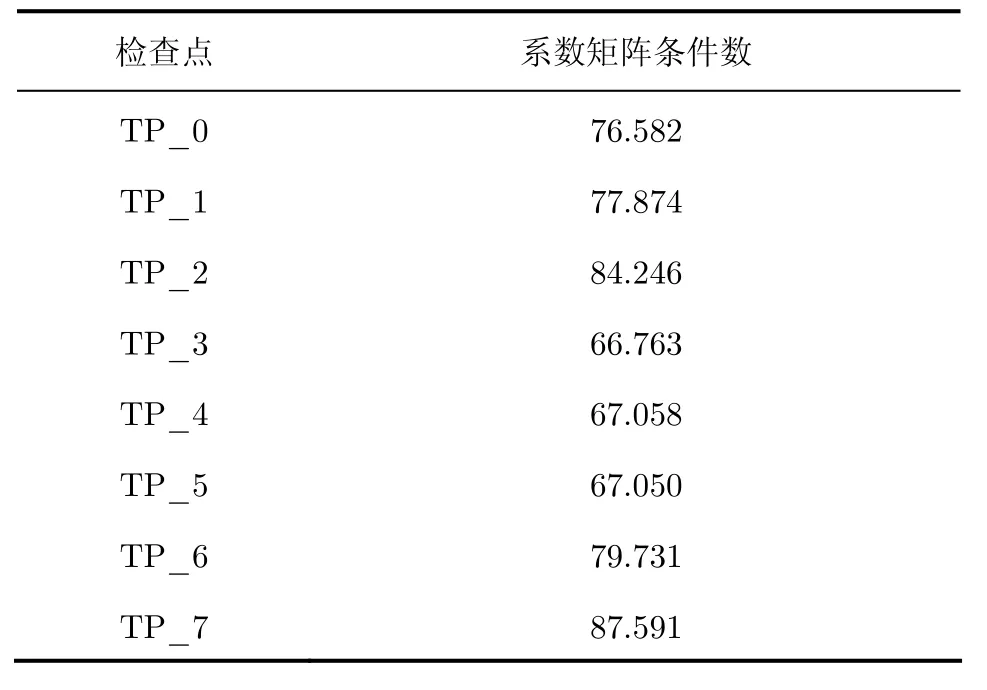
表8 立体像对1各检查点的矩阵条件数Tab. 8 Matrix condition number of each check point in stereo SAR images 1

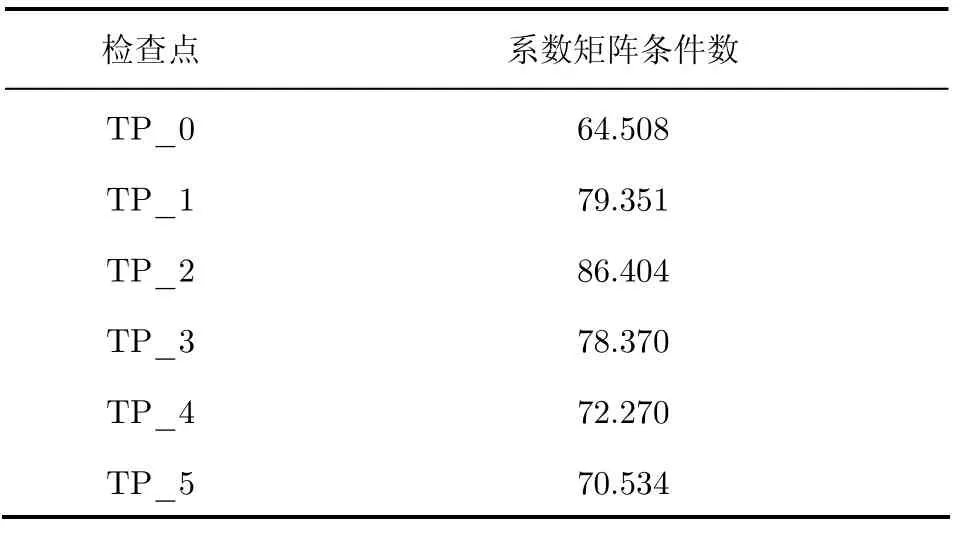
表9 立体像对2各检查点的矩阵条件数Tab. 9 Matrix condition number of each check point in stereo SAR images 2

根据式(2)可知，对于每个检查点而言，其地面3维坐标的求解都是由相应同名像点坐标列出的 4个方程来构成方程组。各检查点对应方程组的条件数与相应同名像点的坐标、视差、基高比(基线长度与相对高程值之比)等因素有关。

从表8和表9可以看出，两个立体像对中所有检查点的条件数均较小，对应的系数矩阵均满秩，各个方程组均无病态问题，保证了本文结果的正确性与可靠性，进而验证了本文方法对交会条件较好的SAR数据的有效性。在SAR图像的立体定位中，需要注意的是：

(1) 为了获得良好的立体定位结果，应尽量选取立体交会条件较好的两轨SAR图像；

(2) 若两次观测的轨迹、视角等近似一致，则难以通过立体测量方式得到可靠的定位结果。

4 总结

选择几何构像模型和定向参数解算方案是实现SAR图像高精度立体定位的关键。针对稀少控制下斜侧视SAR图像高精度立体定位难题，设计了利用单个地面控制点的 SAR图像斜侧视高精度立体定位方案。该方案利用轨道参数获取天线相位中心的位置和速度信息，利用1个地面控制点标定SAR图像的近距延迟和多普勒中心频率，在此基础上由立体像对中的同名像点坐标求解相应地面点的3维坐标。采用中国测绘科学研究院获取的机载SAR图像进行了立体定位实验，统计分析了定位误差，验证了本文方案的精确性和有效性。

实验中所采用的 SAR图像覆盖区域地形起伏较小，后续将进一步研究本文方法在高程起伏较大地区的适用性；为了进一步促进SAR图像立体定位技术的发展和应用，下一步将研究斜侧视SAR图像区域网空中三角测量技术，以实现大区域稀少控制的SAR图像控制点加密与高精度定位。

[1] 张红敏. SAR图像高精度定位技术研究[D]. [博士论文], 信息工程大学, 2013: 1-2.

Zhang Hong-min. Research on technologies of accurate positioning with SAR images[D]. [Ph.D. dissertation], Informational Engineering University, 2013: 1-2.

[2] 靳国旺. InSAR获取高精度DEM关键处理技术研究[D]. [博士论文], 信息工程大学, 2007: 1-3.

Jin Guo-wang. Research on key processing techniques for accurate DEM deriving from InSAR[D]. [Ph.D. dissertation], Information Engineering University, 2007: 1-3.

[3] 靳国旺. InSAR地形测绘若干问题研究[R]. 中国科学院电子学研究所博士后出站报告, 2011: 1.

Jin Guo-wang. Research on key technologies of InSAR topographic surveying and mapping[R]. Institute of Electronics Chinese Academy of Sciences Postdoctoral Report, 2011: 1.

[4] Brown W M. Synthetic aperture radar[J].IEEE Transactions on Aerospace and Electronic Systems, 1967, AES-3(2): 217-229.

[5] Leberl F W. Radargrammetry for image interpretation[R]. ITC Technical Report, 1978: 1-228.

[6] Konecny G, Schuhr W, and Howington-Kraus A. Mapping accuracy using side-looking radar images on the analytical stereoplotter[C]. 15th International Society for Photogrammetry and Remote Sensing Conference, Kyoto, 1988: 474-480.

[7] 张过, 费文波, 李贞, 等. 用RPC替代星载SAR严密成像几何模型的试验与分析[J]. 测绘学报, 2010, 39(3): 264-270.

Zhang Guo, Fei Wen-bo, Li Zhen,et al.. Analysis and test of the subsitutability of the RPC model for the rigorous sensor model of spaceborne SAR imagery[J].Acta Geodaetica et Cartographica Sinica, 2010, 39(3): 264-270.

[8] 程春泉, 张继贤, 邓喀中, 等. 雷达影像几何构像距离-共面模型[J]. 遥感学报, 2012, 16(1): 38-49.

Cheng Chun-quan, Zhang Ji-xian, Deng Ka-zhong,et al.. Range-coplanarity equation for radar geometric imaging[J].Journal of Remote Sensing, 2012, 16(1): 38-49.

[9] Curlander J C. Location of pixels in space borne SAR imagery[J].IEEE Transactions on Geoscience and Remote Sensing, 1982, 20(3): 359-364.

[10] 杨杰, 潘斌, 李德仁, 等. 无地面控制点的星载SAR影像直接对地定位研究[J]. 武汉大学学报(信息科学版), 2006, 31(2): 144-147.

Yang Jie, Pan Bin, Li De-ren,et al.. Location of spaceborne SAR imagery without reference points[J].Geomatics andInformation Science of Wuhan University, 2006, 31(2): 144-147.

[11] 陈尔学, 李增元, 卢颖, 等. 三颗高分辨率星载SAR的定位模型构建及其定位精度评价[J]. 遥感信息, 2010, 2: 43-48.

Chen Er-xue, Li Zeng-yuan, Lu Ying,et al.. Constructiong geo-location models and their geo-location accuracy evaluation of three high resolution satellite SAR [J].Remote Sensing Information, 2010, 2: 43-48.

[12] Leberl F W. Radargrammetric Image Processing[M]. Massachusetts: Artech House, 1990.

[13] 袁修孝, 吴颖丹. 缺少控制点的星载 SAR遥感影像对地目标定位[J]. 武汉大学学报(信息科学版), 2010, 35(1): 88-91.

Yuan Xiu-xiao and Wu Ying-dan. Object location of space-borne SAR imagery under lacking ground control points[J].Geomatics and Information Science of Wuhan University, 2010, 35(1): 88-91.

[14] 张兢, 杨杰, 郎丰铠, 等. 提高无控制点星载SAR影像的定位精度研究[J]. 测绘信息与工程, 2011, 36(5): 17-19.

Zhang Jing, Yang Jie, Lang Feng-kai,et al.. Improving location accuracy of space-borne SAR imagery with out reference points[J].Journal of Geomatics, 2011, 36(5): 17-19.

[15] 张红敏, 靳国旺, 徐青. 基于DEM和图像仿真的单幅SAR图像无控制定位[J]. 测绘科学技术学报, 2013, 30(3): 274-278.

Zhang Hong-min, Jin Guo-wang, and Xu Qing. Positioning with single SAR image based on DEM without ground control point[J].Journal of Geomatics Science and Technology, 2013, 30(3): 274-278.

[16] 李银伟, 韦立登, 向茂生. 机载干涉 SAR运动补偿中地物目标定位误差的影响分析[J]. 雷达学报, 2013, 2(4): 492-498.

Li Yin-wei, Wei Li-deng, and Xiang Mao-sheng. Effects of target positioning error on motion compensation for airborne interferometric SAR[J].Journal of Radars, 2013, 2(4): 492-498.

张红敏(1984-)，女，河北大城人，博士，讲师，主要从事 SAR图像高精度定位技术研究，发表论文10余篇，获得国家技术发明专利3项。

E-mail: zhmin1206@163.com

靳国旺(1977-)，男，河北滦南人，博士，副教授，主要从事摄影测量与遥感、InSAR技术研究。

徐 青(1964-)，男，浙江磐安人，博士，教授，主要从事摄影测量与遥感、空间仿真技术研究。

李向英(1977-)，男，吉林长春，硕士，工程师，主要从事摄影测量技术研究。

Accurate Positioning with Stereo SAR Images and One Ground Control Point

Zhang Hong-min①Jin Guo-wang①②Xu Qing①Li Xiang-ying③

①(Information Engineering University, Zhengzhou 450001, China)
②(Chinese Academy of Surveying and Mapping, Beijing 100039, China)
③(61512 Troops, Beijing 100088, China)

Geometrical imaging models and calculations of orientation parameters are the main factors affecting the positioning of stereo Synthetic Aperture Radar (SAR) images. For accurate positioning with squint stereo SAR images and less Ground Control Points (GCPs), a positioning algorithm with one GCP is designed. In this algorithm, the position and velocity of the radar antenna phase center are derived using orbit parameters, and the close range and Doppler centroid of the SAR images are compensated by one GCP. Thus, accurate orientation parameters are obtained and accurate positioning with stereo SAR images is completed. Airborne SAR images acquired by the Chinese Academy of Surveying and Mapping are used in experiments. The positioning errors of the checkpoints are calculated and analyzed, and it verified the accuracy and effectiveness of the proposed method.

Synthetic Aperture Radar (SAR); Stereo; Positioning; Range-Doppler; Ground Control Point (GCP)

中国分类号：TP75; P237

A

2095-283X(2014)01-0085-07

10.3724/SP.J.1300.2014.13138

2013-12-23收到，2014-03-17改回；2014-03-24网络优先出版

40771142, 40871213, 41071296)和中国测绘科学研究院基本科研业务费项目资助课题

*通信作者： 张红敏 zhmin1206@163.com