卫星姿态导引对Geo-SAR观测特性影响的分析

田雨润 禹卫东 熊名男②

①(中国科学院电子学研究所 北京 100190)

②(中国科学院大学 北京 100190)

卫星姿态导引对Geo-SAR观测特性影响的分析

田雨润*①②禹卫东①熊名男①②

①(中国科学院电子学研究所 北京 100190)

②(中国科学院大学 北京 100190)

卫星姿态导引技术被广泛应用于现有的低轨星载 SAR系统之中，目的在于减轻接收数据中距离/方位向耦合。该文深入分析了卫星姿态导引对地球同步轨道合成孔径雷达(Geosynchronous Synthetic Aperture Radar, Geo-SAR)的多普勒参数、测绘带宽以及距离徙动的影响，对比了Geo-SAR的3种姿态导引方式的效果。通过仿真验证了Geo-SAR进行姿态导引的必要性，表明了基于椭圆轨道的2维导引方法对于Geo-SAR是最有效的。

地球同步轨道合成孔径雷达；姿态导引；多普勒参数；测绘带；距离徙动

1 引言

合成孔径雷达(SAR)具有全天时全天候的观测优势，因此自提出以来就得到了迅速的发展。近几年，许多先进的星载合成孔径雷达系统都被成功发射并运行，提供了大量之前其它类型遥感器无法获得的信息[1]。SAR系统的空间分辨率、时间分辨率和测绘带宽往往是人们最关注的3个方面，因为这三方面决定了对地面目标的可辨识度、对突发事件的响应速度和对地面观测的覆盖范围。对于灾难监视和预测，热点地区监视等情况，高时间分辨率和大观测范围就显得更加重要。

卫星监测系统可以先工作在观测时间间隔较短且观测面积较大的“监控模式”下，一旦有突发事件，再转换到高空间分辨率的工作模式。但目前在轨SAR卫星一般都处于轨道高度200-1000 km的低轨道，卫星重访周期长且观测覆盖范围小。鉴于此，地球同步轨道SAR的概念应运而生[2]，其工作于约36000 km的高空，卫星重访周期为24 h，较之低轨道 SAR以星期为单位的重访周期有了大幅度缩短，并且由于轨道高度的升高，测绘带宽得到增大，因而可以完全胜任“监控模式”的任务需求[3－5]。

但是，随着轨道的升高，也有许多新的问题摆在了我们眼前[6－8]，其中一个重要问题就是地球同步轨道合成孔径雷达(Geosynchronous Synthetic Aperture Radar, Geo-SAR)的超长合成孔径时间所带来的严重距离/方位向耦合，低轨SAR处理此类问题的方法是采用卫星姿态控制技术来实现零多普勒中心[9]。本文对比了现有的几种波束控制方式，选出了一种适用于Geo-SAR的最优方式，并深入分析讨论了该波束控制方式对于 Geo-SAR观测特性的影响，包括其对高阶多普勒参数，测绘带和点目标距离徙动的影响。

2 Geo-SAR多普勒参数分析

2.1 星地几何关系

地心惯性坐标系Eo定义为：原点在地心，Xo轴指向春分点，Zo轴指向北极，Yo轴符合坐标系右手准则。地心转动坐标系Eg定义为：原点在地心，Xg沿赤道面指向本初子午线，Yg轴符合坐标系右手准则。轨道平面坐标系Ev定义为：原点在地心，Xv轴指向近地点；Zv轴垂直于轨道平面与卫星角速度方向相同，Yv轴符合坐标系右手准则。

星载 SAR系统的卫星坐标系一般初始化为一个坐标轴指向地心，本文定义卫星坐标系Es为：原点处于卫星质心，Xs轴由地心指向相位中心，Ys轴垂直于Xs指向速度方向，Zs轴符合坐标系右手准则垂直于轨道平面。各个坐标系定义如图1所示。

图中Rs为卫星在Eo中的位置向量，Rt为波束中心处点目标在Eo中的位置向量，γ为下视角，γ取负值时表示波束右视，正值表示波束左视。

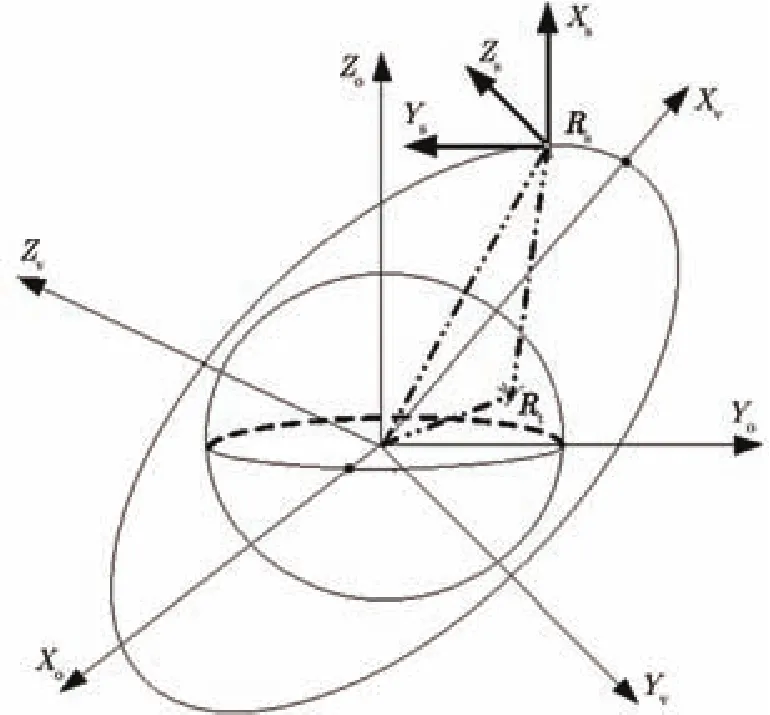
图1 Geo-SAR空间几何关系Fig. 1 Geometry structure of Geo-SAR

2.2 Geo-SAR和波束中心处目标的状态描述

设卫星在Eo中的速度向量为Vs，加速度向量为As, 2阶加速度向量为A2s, 3阶加速度向量为A3s。点目标在Eo中的位置向量为Rt，速度向量为Vt，加速度向量为At, 2阶加速度向量为A2t, 3阶加速度向量为A3t。

卫星运动矢量之间和目标运动状态矢量之间满足：

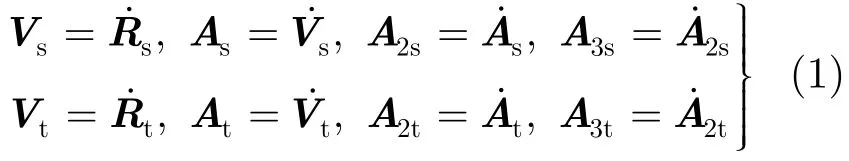
在Ev中求得卫星位置向量和速度向量为：

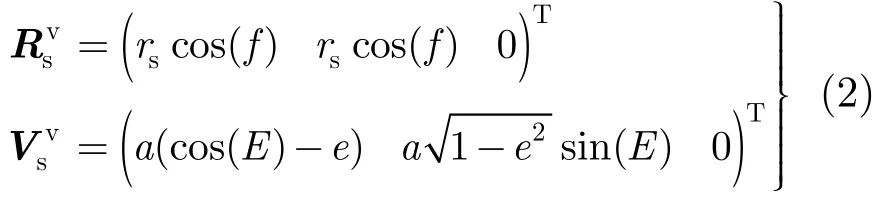
其中f为真近点角，a为轨道半长轴，E为平近点角，由Ev到Eo的旋转矩阵为：

其中w是近地点幅角，i是轨道倾角，ς是升交点赤经。故R

由万有引力定律可知：

其中，μ为引力常数。

按式(1)整理可得：

对于地面点目标，随地球在Eo中做匀速圆周运动，于是由式(1)可以求得：

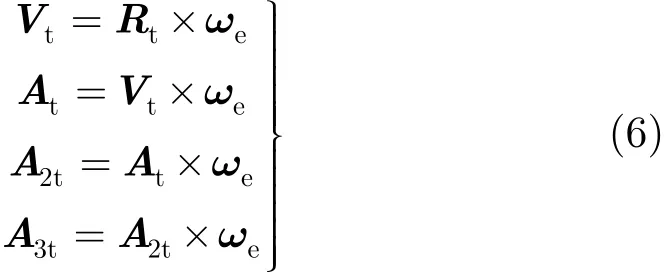
2.3 多普勒参数计算

任意坐标系下，多普勒中心fd，多普勒调频率f1r，多普勒2阶调频率f2r，多普勒3阶调频率f3r的计算表达式为：

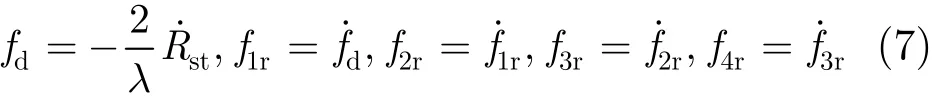
其中λ为载波波长，。将式(7)展开可得：

2.4 2维姿态导引

当卫星未进行姿态导引时，波束指向处点目标在Es中的坐标为：

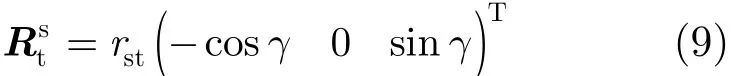
2维姿态导引控制需要通过调整波束偏航角和俯仰角实现，本文采用先偏航再俯仰的控制顺序。设偏航角为θy，俯仰角为θp，二者均以逆时针为正方向，则经过2维姿态控制之后的波束指向处点目标在Es中的坐标为：

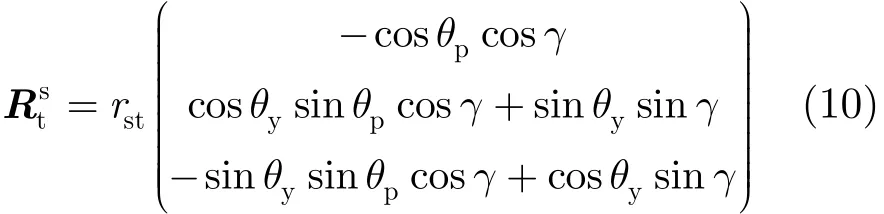
rst此时为未知量。由于点目标处在地球表面，因此只需将式(10)转换到地心转动坐标系Eg中，然后带入地球表面在Eg中的坐标方程即可。则根据地球WSG-84模型，地球在Eg中的椭球方程为：

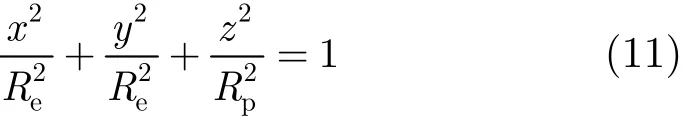
由于Eg与Eo之间的转换仅是沿Zg旋转1个春分点的格林威治角，且椭球方程中x与y对应的轴长都为Re，所以可简化一步转换，仅将式(10)转换到Eo之中就可直接带入式(11)进行求解。得到rst之后，将式(10)转化至Eo中，得到：

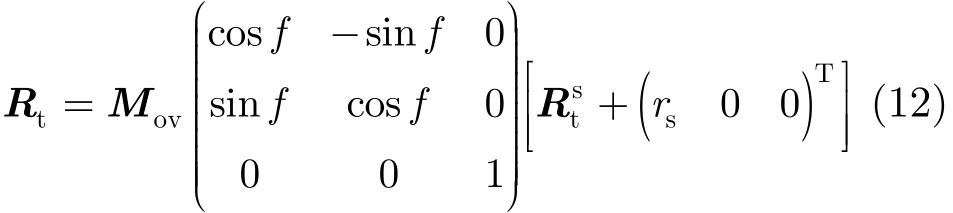
从而将Rt带入式(11)，可求得点目标运动的各个状态矢量。

3 仿真实验及结果分析

系统仿真参数如表1所示。

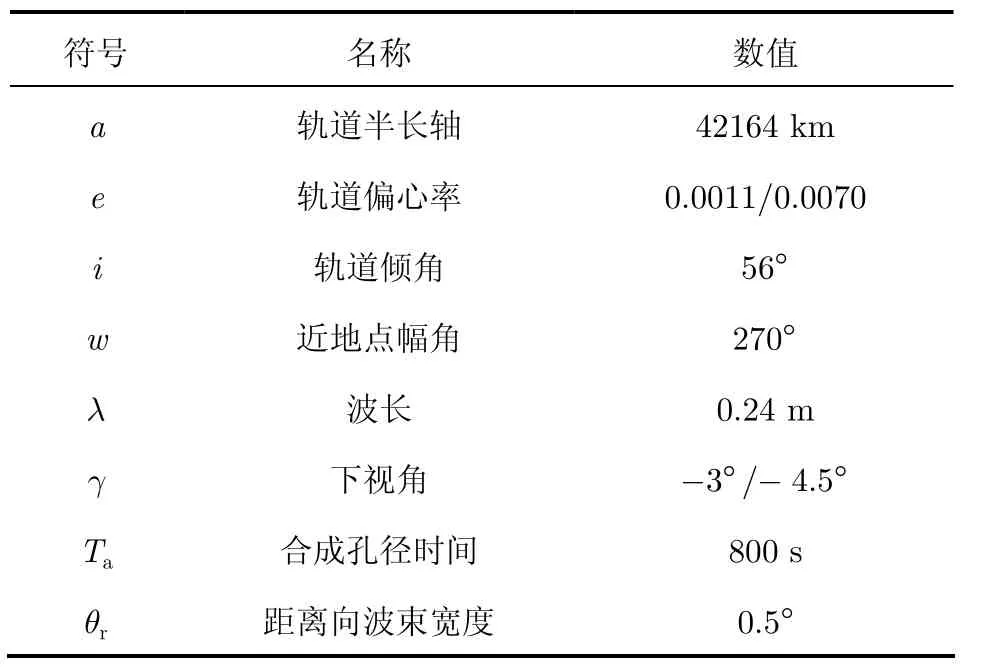
表1 仿真中所用Geo-SAR参数Tab. 1 Simulation parameters for Geo-SAR

地球自转和轨道偏心率是影响星载 SAR多普勒中心的两大因素。

卫星姿态导引的基本原理就是通过控制波束指向抵消地球自转和轨道偏心率对多普勒中心的影响。

取轨道离心率为0.0011，则当轨道高度在10000 km到43000 km之间变化时，对每种轨道高度下卫星单个轨道周期内多普勒中心的变化情况进行考察，如图2所示。

由图2可知，卫星轨道升高会使得卫星速度降低，从而地球自转效应变得不可忽略，其对多普勒中心的影响随着轨道高度的上升而增加。

选取轨道高度为42164 km，考察多普勒中心随轨道偏心率变化而变化的情况，如图3所示。

由图3可知，当轨道偏心率在0增至0.0070之间变化时，多普勒中心随之显著增加。

3.1 3种姿态导引方式对比

本节选取 3种波束导引方式进行对比，方式 1是文献[10]中提出的适用于圆轨道的方式，该方式仅利用1维偏航角导引，即：

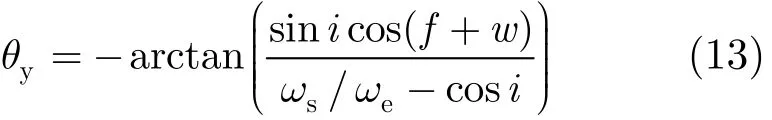
对于正圆轨道星载 SAR该方式可以实现零多普勒中心。

方式2为文献[11]中提出的应用于TerraSAR-X的2维导引方式，在方式1的基础上添加了俯仰角，即：

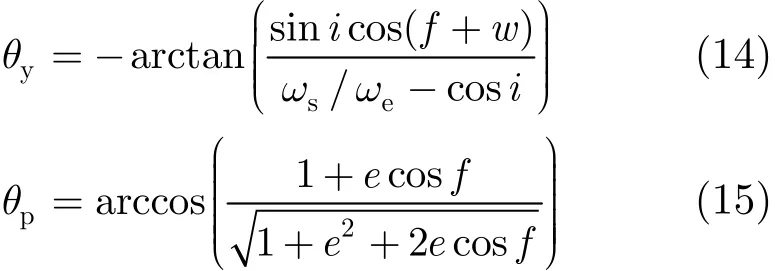
由式(13)、式(14)可知方式1与方式2的偏航角公式完全相同，方式2相对于方式1的改进就在于增加了俯仰控制。

方式3为文献[12]中提出的基于矢量分析法得到的偏航与俯仰角，可以实现在任意偏心率下全轨道周期内多普勒中心为0，与轨道高度无关，即：

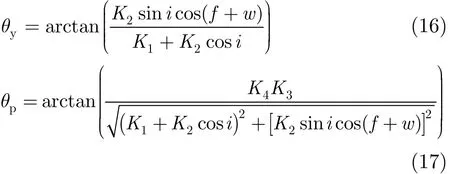
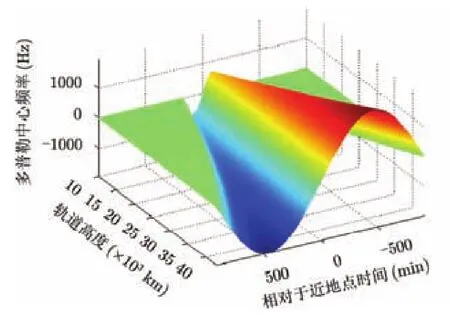
图2 多普勒中心随轨道高度的变化情况Fig. 2 The impacts of orbit height on Doppler

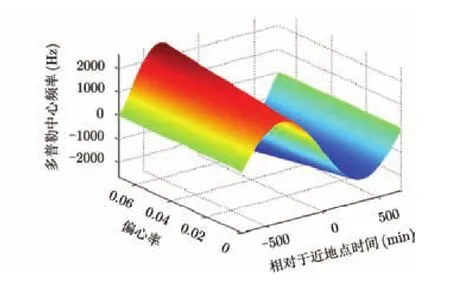
图3 多普勒中心随轨道偏心率变化 Fig. 3 The impacts of eccentricity on Doppler center

式中：

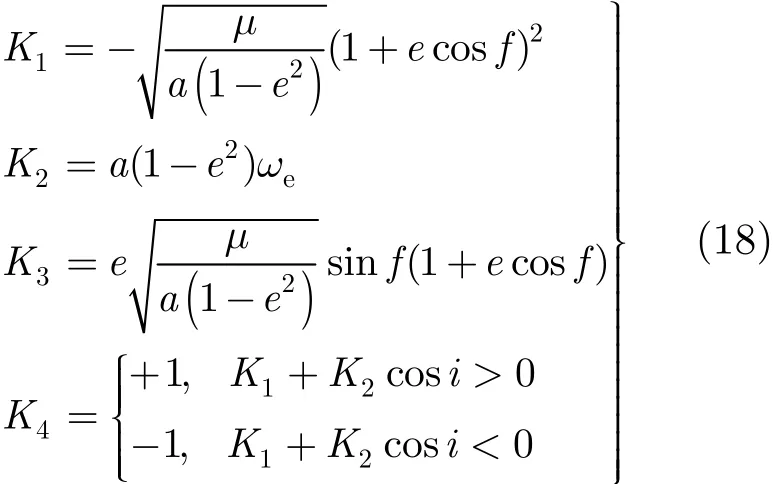
对比3种导引方式作用于Geo-SAR的残余多普勒中心，如图4所示。

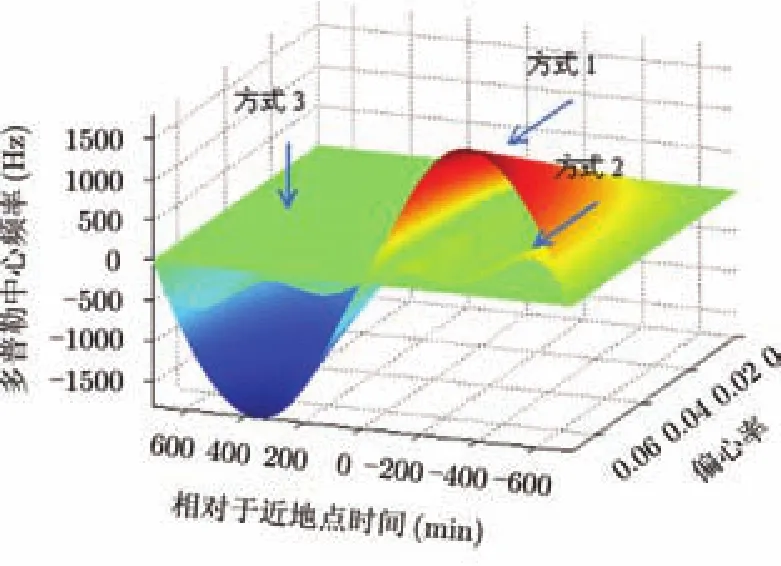
图4 3种导引方式对比Fig. 4 Comparison of the three attitude steering methods

由图4可知，方式1对轨道偏心率最敏感，方式2次之，方式3可以实现任意轨道偏心率下多普勒中心为0。方式1只有1维偏航角控制，虽然能抵消部分地球自转的影响，但完全没有顾及轨道偏心率，所以轨道偏心率增加时方式1导引的效果下降；方式2虽然比方式1有所改进，但是由于其俯仰角只是采用近似公式，不能使波束指向时刻垂直于相对速度方向，所以也不能保证任意偏心率下多普勒中心残余为0。虽然在偏心率为0.0011时，最大残余多普勒中心只在±20 Hz左右，但由于 Geo-SAR的高轨道特性，与目标相对速度较小，多普勒带宽一般在 100 Hz以内(例如卫星处于纬度幅角时，合成孔径时间为 800 s，多普勒带宽约为67 Hz)，所以可见20 Hz的残余多普勒中心也会给数据处理带来很大影响；方式3能够不受轨道偏心率及地球自转影响，始终保证在全轨道周期内多普勒中心为0，因此导引效果最佳。

以下分析均设定轨道偏心率为 0.0011，姿态导引采用方式3。

3.2 高阶多普勒参数分析

文献[13-15]中提出的针对高轨道 SAR的成像算法需要用高阶多普勒参数来拟合斜距，文献[16]对高阶多普勒参数进行了分析。因此有必要考察波束控制对其造成的影响。本节仿真了1至4阶多普勒调频率，对控制对高阶多普勒参数的影响，如图5所示。

从仿真结果可以看出，波束控制在保证多普勒中心为0的同时还会影响高阶多普勒参数，使高阶多普勒参数随卫星所处轨道位置的变化幅度增大，因而会增大方位向信号的空变性。

3.3 测绘带宽分析

姿态导引会对观测任务产生影响，因为与低轨道SAR相比，Geo-SAR的偏航与俯仰控制所需角度较大，其对测绘带形状及位置可能有较大影响，仿真结果如图6所示，其中图6(c)中测绘带宽对比e=0.0011，下视角为4.5°，波束宽度为0.5°。

由图6(a)，图6(b)可知，姿态导引对于测绘带形状的影响非常显著，尤其是在远地点附近，较之未导引的情况有极大的改变。又由图6(c)可以看出，其对测绘带宽的影响不是很明显，虽然会使测绘带宽在轨道周期内变化性更强，但对其变化范围影响不大，只有2 km左右。

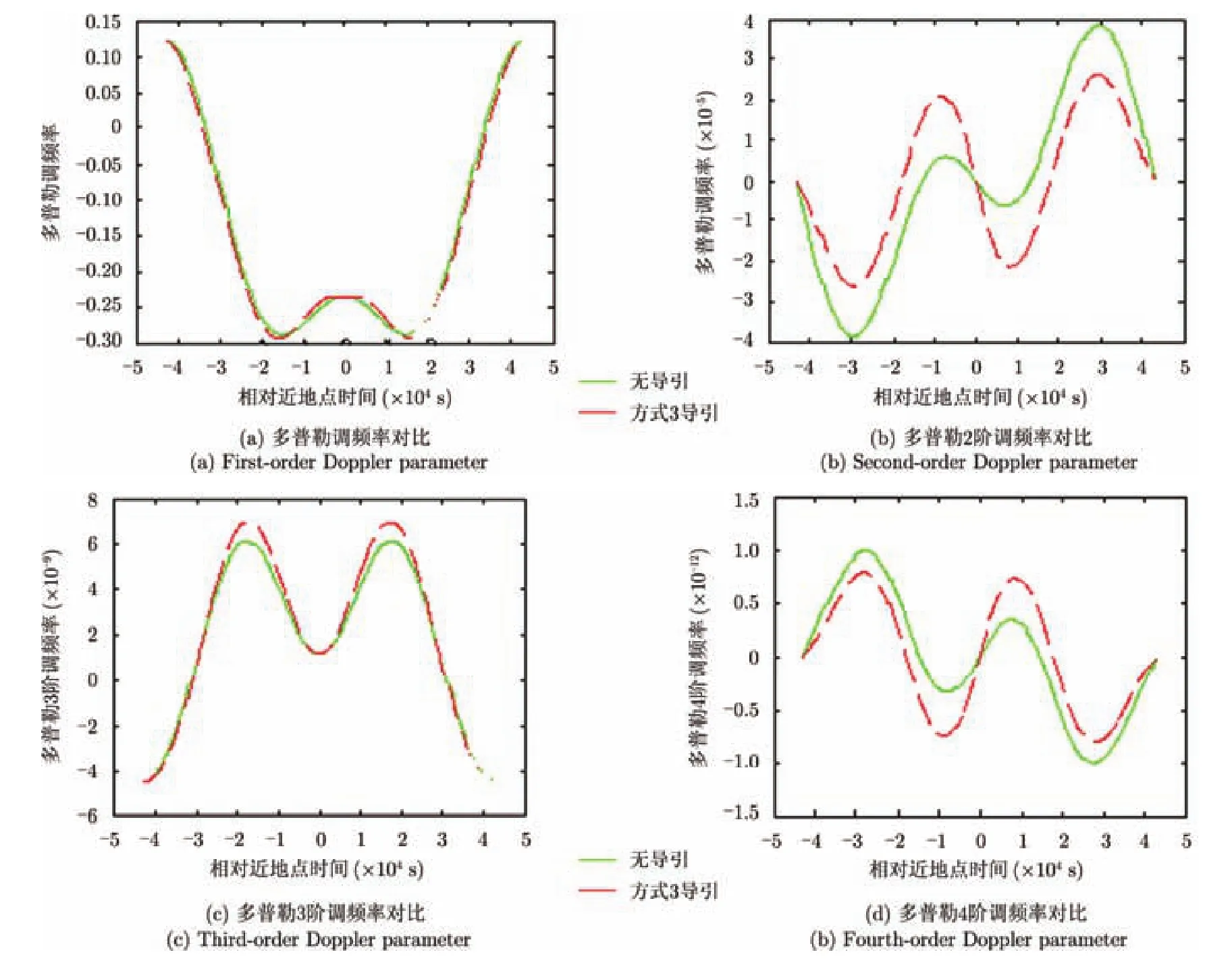
图5 姿态导引对高阶多普勒参数的影响Fig. 5 The impacts of attitude steering on high-order Doppler parameters

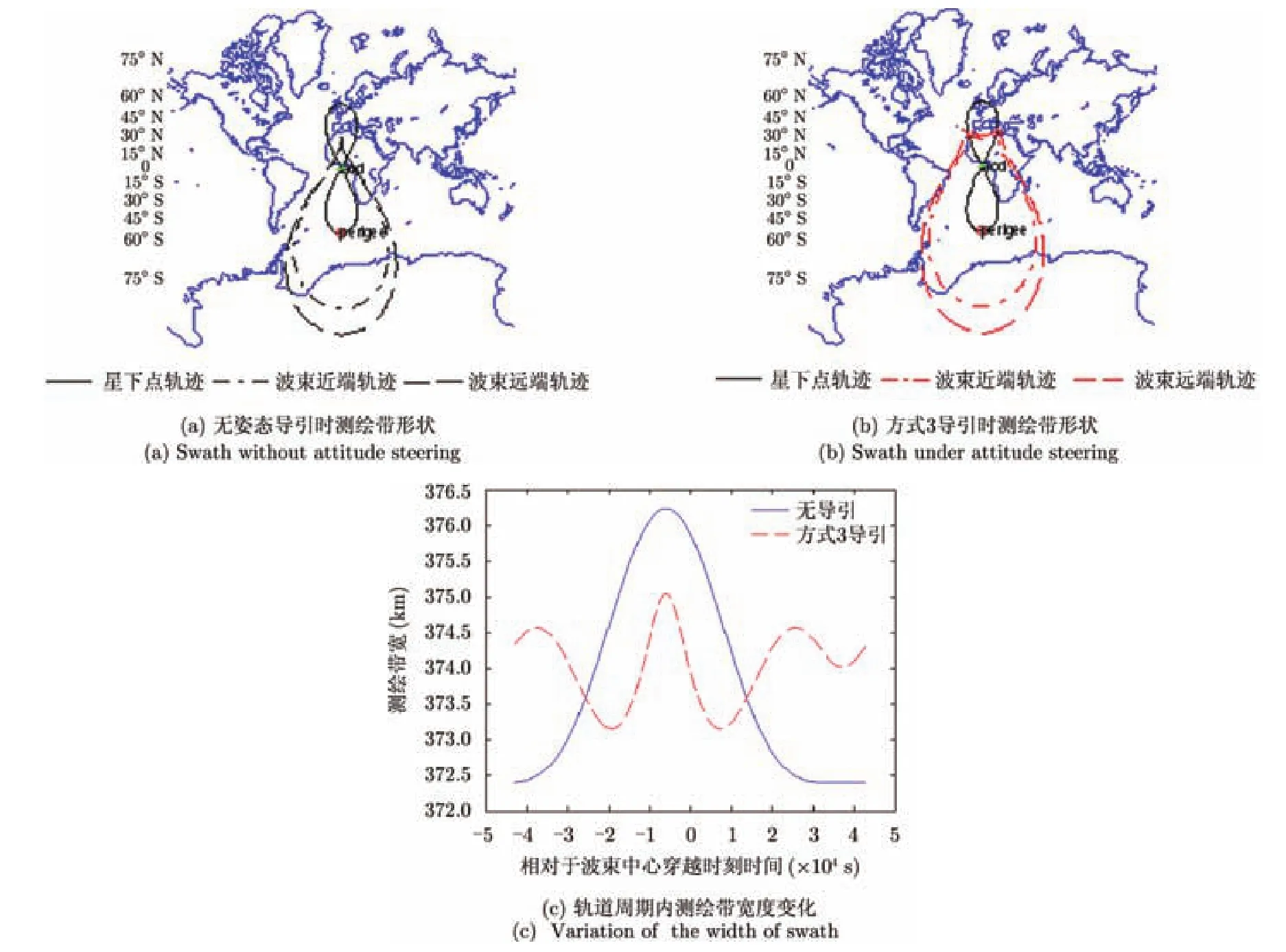
图6 姿态导引对测绘带特性的影响Fig. 6 The impacts of attitude steering on swath

由于Geo-SAR的超高轨道高度，故在一定的距离向波束宽度下，下视角的微小变化可能导致测绘带宽的剧烈变化。

图 7为雷达右视，下视角的变化范围为3°到4.5°的条件下，卫星在整个轨道周期内测绘带宽的变化情况，由图7可知，下视角只改变了1.5°(3°～4.5°)就导致了50 km测绘带宽的变化，因此可知，对于Geo-SAR，非常有必要结合卫星姿态导引方式来设计观测任务。

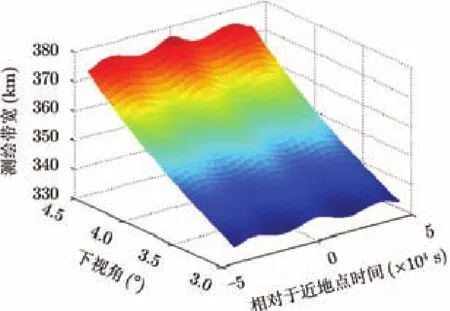
图7下视角对测绘带宽度的影响Fig. 7 The impacts of down look angle on swath width

3.4 距离历程分析

先选择3个卫星位置：近地点、远地点、升交点，来考察卫星在这个3个观测点时波束控制对点目标距离徙动的影响，如图8所示。

从图 8(a)和图 8(b)中可以看出姿态导引在近/远地点没有影响点目标的距离历程，这是因为在近/远地点即使不进行波束控制，其多普勒中心本身也为零。由图8 (c)和图8(d)可以看出在不进行姿态导引的情况下，距离历程“斜视”效果明显，波束中心穿越时刻不对应点目标的最近斜距，且相对于波束中心穿越时刻的距离徙动量大。当以方式3对波束进行控制后，波束中心穿越时刻对应点目标的最近斜距，完全克服了“斜视效果”。

从图8(c)和图8(d)可以看出，对于升交点来说，在不进行姿态导引时，距离徙动量随合成孔径时间增加快速增加，但通过姿态控制可以很好地抑制目标的距离徙动量。

远地点处点目标的距离历程为“近远近”形式，这是由于Geo-SAR的轨道高度和离心率造成的，对于低轨道SAR或者偏心率为0的Geo-SAR不会出现此现象。在远地点附近区域都会有此种距离历程，如图9所示。

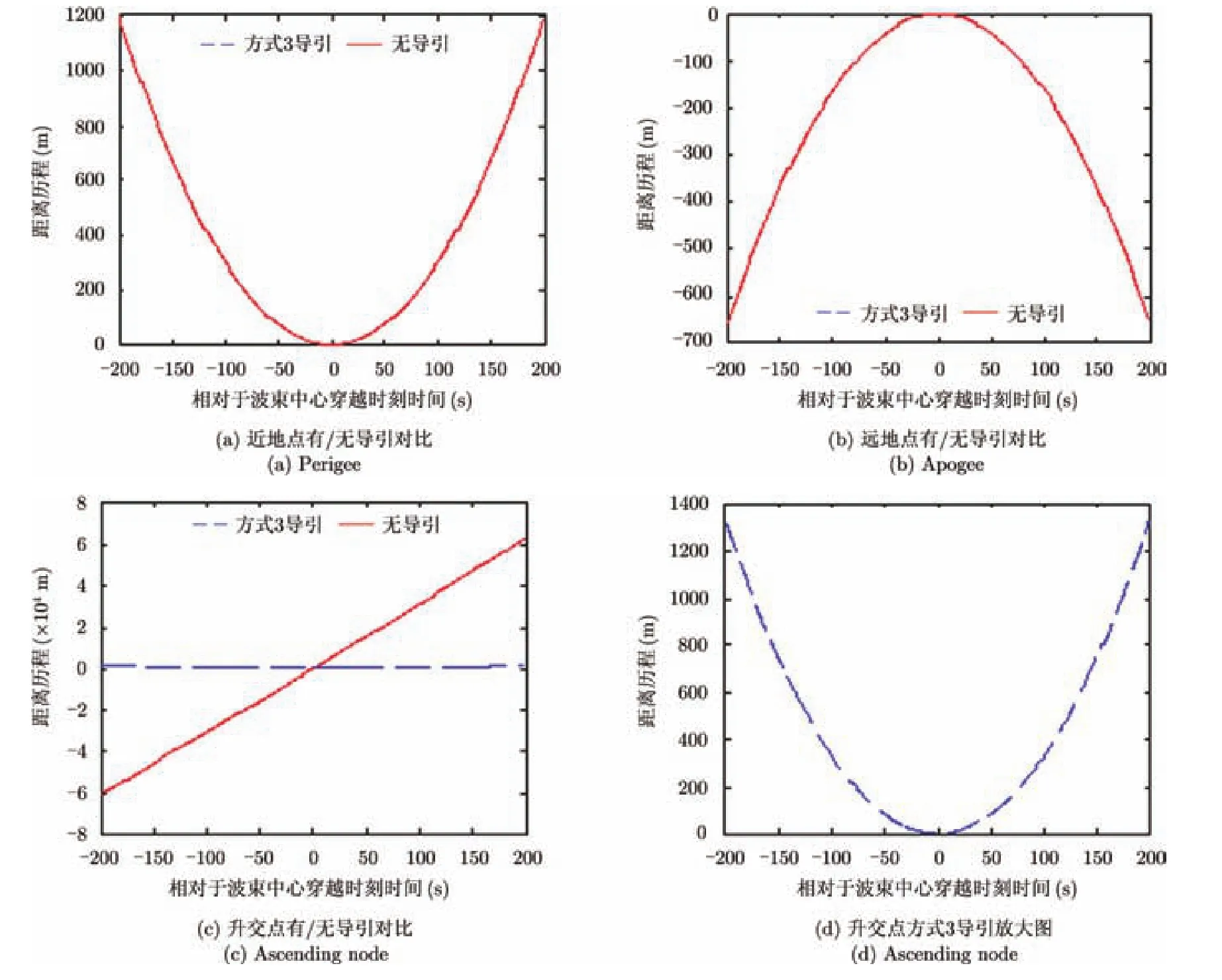
图8 卫星处于近/远地点和升交点时的点目标距离历程Fig. 8 The range migration of certain points target

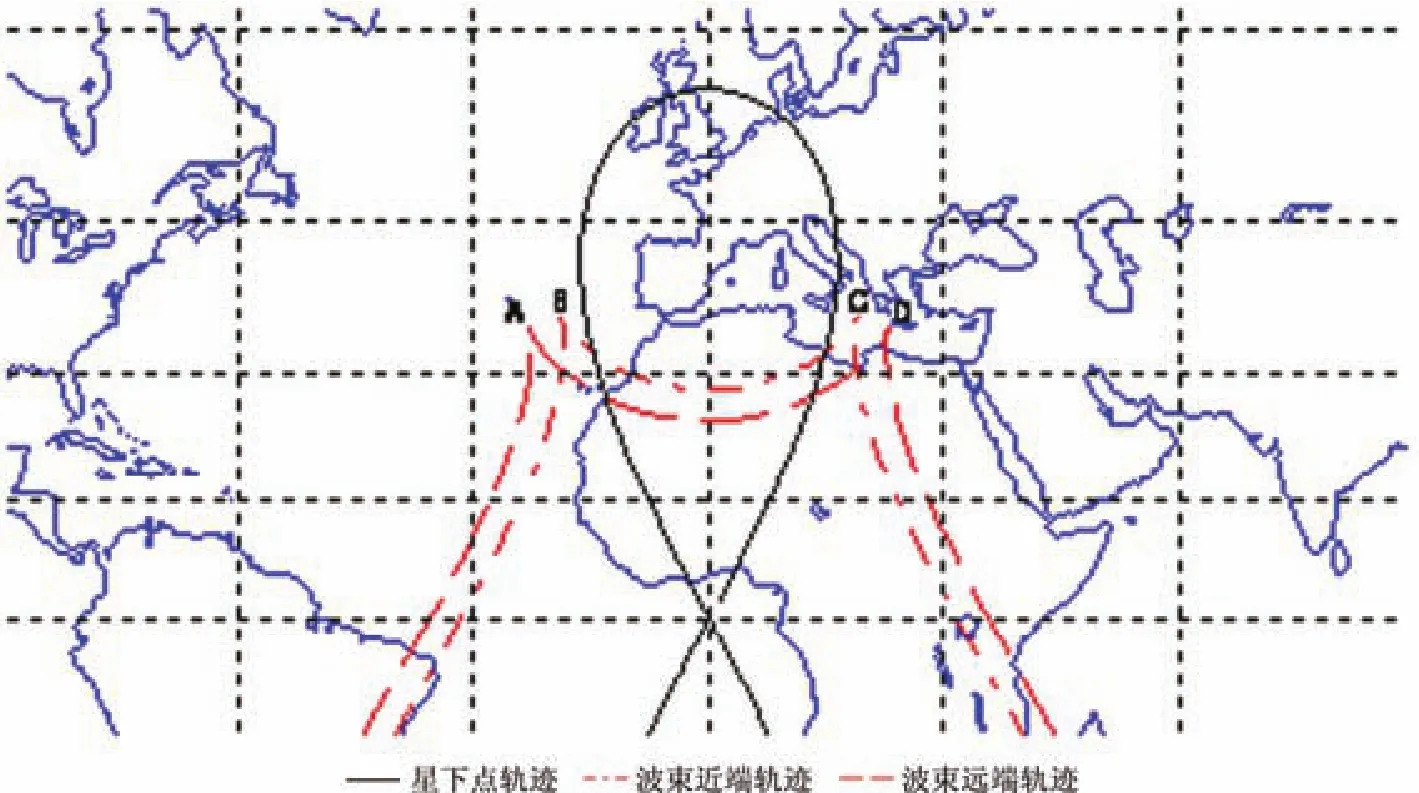
图9 远地点测绘带局部图Fig. 9 Swath near apogee

处于测绘带ABCD内的点目标的距离历程特行都会为“近远近”型，这种特殊的距离历程形式决定的无法再使用等效斜视角的概念(此时等效斜视角为复数)，因此有必要采用新的成像斜距模型，其中高阶多普勒参数拟合模型可以很好地解决这一问题。

在不进行姿态导引时，距离徙动量随合成孔径时间增加快速增加，但通过姿态控制可以很好地抑制目标的距离徙动量，考察卫星处于升交点时景中心点目标，仿真结果如图10所示。

由图10以看出，经过波束控制之后，最大距离徙动量随合成孔径时间的增长趋势明显减弱，多普勒中心变为 0 Hz，距离/方位向耦合明显减弱，对于后续成像处理有很大帮助。

4 结论

本文在地心惯性坐标系下推导了Geo-SAR的高阶多普勒参数。对比了现有的几种卫星姿态导引方式应用于Geo-SAR的效果，通过仿真实验比较得出了最优的导引方式，并分析了此最优波束控制方式对各阶多普勒参数、测绘带宽和地面目标距离徙动量的影响。由本文的仿真结果可知，Geo-SAR合成孔径时间长，多普勒带宽小，距离徙动量大，而通过卫星2维姿态导引可以有效地减轻回波数据的距离/方位耦合，因此非常有必要进行卫星姿态导引来降低数据处理难度，并且需要结合卫星姿态导引方式来设计观测任务。

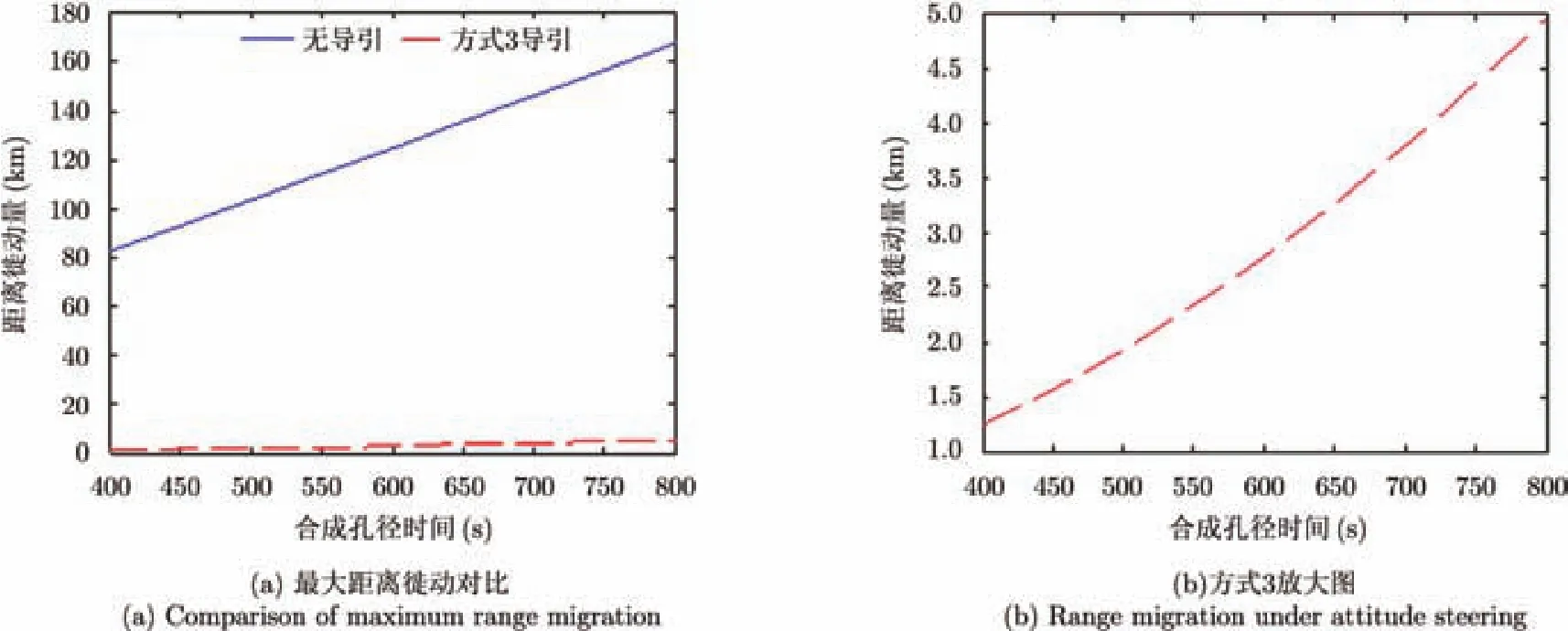
图10 距离徙动随合成孔径时间变化对比Fig. 10 The impact of synthetic aperture time on range migration

[1] 邓云凯, 赵凤军, 王宇. 星载 SAR技术的发展趋势及应用浅析[J]. 雷达学报, 2012, 1(1): 1-10. Deng Yun-kai, Zhao Feng-jun, and Wang Yu. Brief analysis on the development and application of spaceborne SAR[J].Journal of Radars, 2012, 1(1): 1-10.

[2] Tomiyasu K and Pacelli J L. Synthetic aperture radar imaging from an inclined geosynchronous orbit[J].IEEE Transactions on Geoscience and Remote Sensing, 1983, 21(3): 324-329.

[3] Madsen S N, Chen C, and Edelstein W. Radar options for global earthquake monitoring[C]. International Geoscience and Remote Sensing Symposium(IGARSS), Toronto, Canada, 2002: 1483-1485.

[4] Madsen S N, Edelstein W, and Didomenico L D. A geosynchronous synthetic aperture radar for tectonic mapping, disaster management and measurements of vegetation and soil moisture[C]. International Geoscience and Remote Sensing Symposium (IGARSS), NSW, Sydney, 2001: 447-449.

[5] Andrea M G, Stefano T, Fabio R,et al.. GEMINI: geosynchronous sar for earth monitering by interferometry and imaging[C]. International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 2012: 210-213.

[6] Mao Er-ke, Long Teng, Zeng Tao,et al.. State-of-art of geosynchronous SAR[J].Signal Processing, 2012, 28(4): 452-462.

[7] Gao Yang-te, Hu Cheng, Dong Xi-chao,et al.. Accurate system parameter calculation and coverage analysis in GEO SAR[C]. The 9th Eurpean Conference on Synthetic Aperture Radar (EUSAR), Nuremberg, Germany, 2012: 607-610.

[8] Runge H. Benefits of antenna yaw steering for SAR[C]. International Geoscience and Remote Sensing Symposium (IGARSS), Espoo, Finland, 1991: 257-261.

[9] Chang C Y and Curlander J C. Attitude steering for space shuttle based synthetic aperture radars[C]. International Geoscience and Remote Sensing Symposium (IGARSS), Houston, TX, USA, 1992, 1: 297-301.

[10] Raney R K. Doppler properties of radars in circular orbit[J].International Journal of Remote Sensing, 1986, 7(9): 1153-1162.

[11] Fiealer H, Boerner E, Mittermayer J,et al.. Zero dopplersteering—a new method for minimizing the doppler centroid[J].IEEE Geoscience and Remote Sensing Letters, 2005, 2(2): 141-145.

[12] Yu Ze, Zhou Yin-qing, Chen Jie,et al.. A new satellite attitude steering approach for zero doppler centroid[C]. Proceedings of IET International Radar Conference, Gulin China, 2009: 1-4.

[13] Huang Li-jia, Hu Dong-hui, Ding Chi-biao,et al.. A general two-dimensional spectrum based on polynomial range model for medium-earth-orbit synthetic aperture radar signal processing[C]. Proceedings of 2nd International Conference on Signal Processing Systems (ICSPS), Dalian, China, July 2010, 3: 662-665.

[14] Zhao Bing-ji, Qi Xiang-yang, Song Hong-jun,et al.. An accurate range model based on the fourth-order doppler parameters for geosynchronous SAR[J].IEEE Geoscience and Remote Sensing Letters, 2014, 11(1): 205-209.

[15] Wu Xiu, Zhang Shun-sheng, and Xiao Bo. An advanced range equation for geosynchronous SAR[C]. Proceedings of IET International Conference, Shenzhen, China, 2012: 1-4.

[16] Zhao Bing-ji, Qi Xiang-yang, and Song Hong-jun. The accurate fourth-order doppler parameters calculation and analysis for geosynchronous SAR[C]. The 9th Eurpean Conference on Synthetic Aperture Radar (EUSAR), Nuremberg, Germany, 2012: 615-618.

田雨润(1988-)，男，河北唐山人，中国科学院电子学研究所硕士研究生，研究方向为地球同步轨道SAR。

E-mail: leonbel@163.com

禹卫东(1969-)，男，中国科学院电子学研究所，研究员，博士生导师，研究方向为星载SAR系统设计、高分辨率SAR新体制、多极化SAR、干涉SAR等。

E-mail: ywd@mail.ie.ac.cn

熊名男(1989-)，男，湖北汉川人，中国科学院电子学研究所在读研究生，研究方向为新体制合成孔径雷达系统设计及信号处理。

E-mail: xiongmingnan@163.com

Observation Properties Analysis of Geo-SAR with Attitude Steering

Tian Yu-run①②Yu Wei-dong①Xiong Ming-nan①②

①(Institute of Electronics, Beijing 100190, China)
②(University of Chinese Academy of Sciences, Beijing 100190, China)

Attitude Steering has been widely applied to the current low orbit SAR system to decrease the rang/ azimuth coupling of the received data. This paper focuses on the impacts of attitude steering to the observation properties of Geo-SAR, namely, Doppler parameters, range swath, and rang cell migration effect, and a comparisonbetween 3 different ways of attitude steering is made. Based on the simulation results, the necessity of attitude steering for Geo-SAR is validated, and for Geo-SAR on elliptical orbit, 2D attitude steering is the most effective.

Geosynchronous Synthetic Aperture Radar (Geo-SAR); Attitude steering; Doppler parameters; Swath; Range cell migration

中国分类号：TN958

A

2095-283X(2014)01-0061-09

10.3724/SP.J.1300.2014.13114

2013-11-14收到，2014-01-26改回；2014-02-17网络优先出版国家部委基金资助课题

*通信作者： 田雨润 leonbel@163.com