基于极化干涉SAR反演植被高度的改进三阶段算法
2014-08-05许丽颖李世强邓云凯
许丽颖 李世强 邓云凯 王 宇
①(中国科学院电子学研究所 北京 100190)
②(中国科学院大学 北京 100049)
基于极化干涉SAR反演植被高度的改进三阶段算法
许丽颖*①②李世强①邓云凯①王 宇①
①(中国科学院电子学研究所 北京 100190)
②(中国科学院大学 北京 100049)
利用极化干涉合成孔径雷达(Polarimetric Interferometry SAR, PolInSAR)数据反演森林参数问题为当前PolInSAR研究的热点问题。经典的森林参数反演算法是基于随机散射体模型(Random Volume over Ground, RVoG)的阶段反演算法,该算法中直线拟合误差和体散射估计误差会严重影响反演精度。为了提高树高估计精度,该文使用整体最小二乘法直线拟合得到更精确的地表相位估计结果,并提出以Gamma函数为线性度量自适应地估计体散射去相干,得到了改进的PolInSAR三阶段反演算法,实验结果表明改进算法可靠有效。
极化干涉合成孔径雷达(PolInSAR);整体最小二乘法(TLS);树高反演;随机散射体模型(RVoG)
1 引言
植被高度反演对整个陆地系统稳定性和循环平稳性的研究具有重要意义。极化干涉雷达(Polarimetric SAR Interferometry, PolInSAR)通过对极化和干涉信息的有效组合,既具有干涉SAR对散射体位置、分布、运动、变化信息敏感的特点,也具有极化SAR对散射体结构、方向、对称性、纹理以及介电常数等敏感的特性[1]。它可以同时提取观测对象的空间3维结构特征信息和散射信息,使微波定量遥感如树高反演、高精度数字高程(DEM)提取和细微形变提取成为可能。经典的森林高度反演算法是由Cloude和Pathanassiou提出的三阶段反演算法,该算法将反演过程分为相干系数估计和直线拟合、地表相位估计、体散射去相干和参数估计3步[2]。其中高精度直线拟合是提高参数估计精度的基础,直线拟合误差会直接影响到地表相位估计精度,进而严重影响到参数反演精度。同时当体散射去相干估计存在误差时,三阶段反演方法也将面临严重的植被高度反演误差。近年来,为了提高树高反演精度很多学者研究了改进的三阶段反演算法[3],如陈兵等人[4]在2008年提出利用相位最优相干技术估计体散射去相干来提高反演精度,周广益等人[5]在2009年提出树高反演置信度参数并利用该参数改进三阶段反演算法等。但是这些改进算法并未研究直线拟合误差对树高估计精度的影响这一基础问题,直线拟合方法都采用最小二乘法(LS),这种拟合方法存在仅考虑自变量中的误差没有考虑因变量误差的缺陷,使拟合存在误差[6]。另外,通过深入研究体散射相干系数的估计方法,进一步提高体散射相干系数的估计精度对提高树高反演精度也有重要意义。
在理论情况下,Cloude等人[7,8]提出森林地区不同极化方式下的复相干系数在相干复平面上为一条线段,线段一端与单位圆的交点为地面相位点,拟合的可视线段中距离地表相位最远的相干系数点为随机体散射复相干系数。实际数据中存在很多误差,如SNR降低时,观测到的复相干系数存在误差,因此会偏离理想相干直线,从而使得直线段分布变为区域分布,且分布范围随误差增大而增大,复相干系数点在相干复平面上分布的线性度量可以用Gamma函数计算。传统三阶段反演算法直接选用HV通道的相干系数作为体散射相干系数值,会过低估计森林高度。本文利用线性度作为度量手段,自适应地选择参数估计方法:若线性度高,则满足随机散射模型,定义相干区域和拟合直线的交点作为体散射相干系数,使体散射相干系数的估计值更加精确;若线性度低,则采用相位最优相干系数作为体散射相干系数值,进而获得更高的植被参数的反演精度。另外,利用整体最小二乘法(TLS)进行直线拟合,能够同时考虑自变量与因变量中的误差(也就是同时考虑复相干系数实部和虚部的误差),减小直线拟合误差,提高地表相位的估计精度[9,10]。Cloude等人在文献[2]虽然提出过该方法,但是没有给出拟合及参数反演结果。本文利用TLS进行直线拟合,得到了更精确的地表相位估计精度,并提出采用自适应方法估计体散射去相干,因此可以改善树高反演精度。
论文第2节和第3节介绍了整体最小二乘算法和相干区域边界的提取方法,第4节和第5节分别给出了改进的三阶段反演算法和实验结果,实验结果表明本文算法能提高反演精度。
2 整体最小二乘法直线拟合
整体最小二乘法(TLS)能同时考虑自变量与因变量中的误差,可以达到更高的拟合精度[9,10]。若存在观测自变量x和因变量y,对应存在的测量误差分别为vxi和vyi,则直线拟合过程就是利用观测量估计直线斜率a和斜距b的过程。设直线方程为
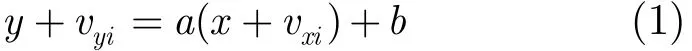
当有n对观测量时,将式(1)写为矩阵形式
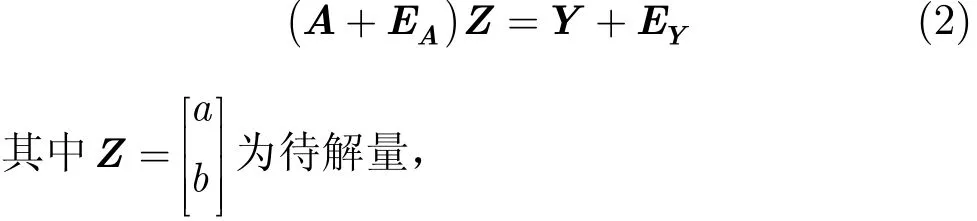
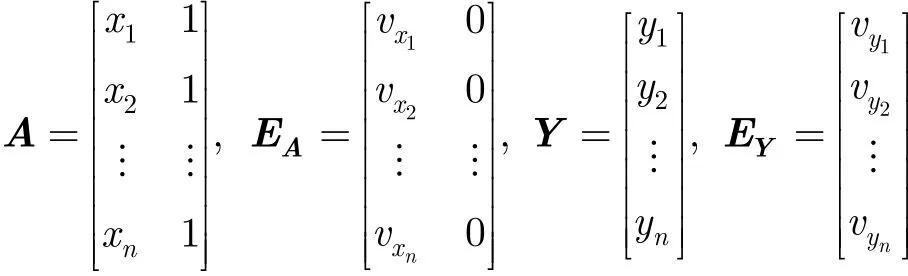
式(1)可等价写为
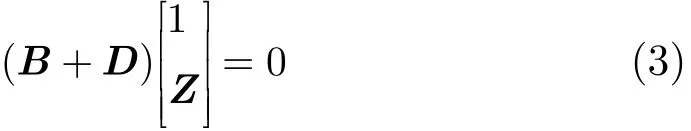
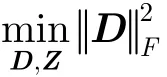
(1) 对增广矩阵B进行奇异值分解(SVD),其中B为n×3维矩阵。
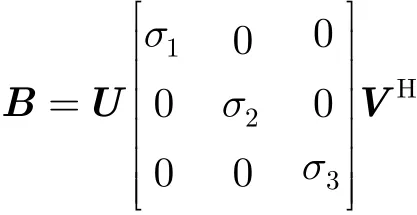
并存储矩阵V=[v1,v2,v3],V的3个特征向量分别对应3个特征值。
(2) 判断主奇异值的个数p,利用公式σp>σ3+ε≥σp+1≥…σ3。
(3) 令
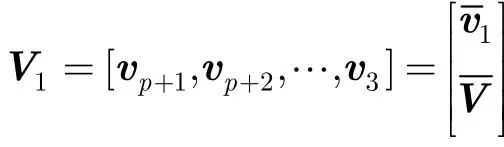
其中是V1的第 1个行向量,可以得到 TLS解也就是得到直线的斜率a和斜距b,进而得到拟合直线。
由于TLS方法同时考虑了自变量和因变量的误差,拟合结果更准确,所以可以利用TLS方法改进传统的三阶段反演算法得到更精确的反演结果。
3 相干区域边界提取
相干区域是指所有复干涉相干系数在复平面内的分布区域[11],相干区域边界可以利用相位旋转法计算。主辅通道极化方式相同的情况下,在任意散射基下的复相干系数定义为:
H
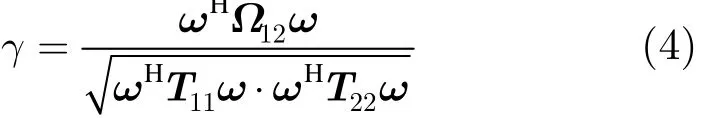
其中,ω是主辅图像对应的散射机制,Ω12是主辅图像的极化互相干矩阵,T11和T22分别是两幅图像的相干矩阵。为了简化计算,将相干系数修正为:

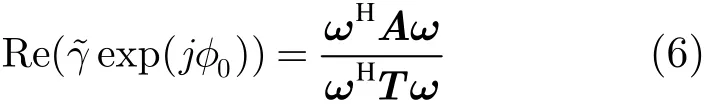
应当注意每个φ0对应一个地表相位,根据式(6)计算会产生一对相干区域边界点,所以相干区域边界密度由采样间隔决定。越密集就越精确,但是计算效率越低。利用拉格朗日乘子法求解式(6)的极值,复拉格朗日函数为:
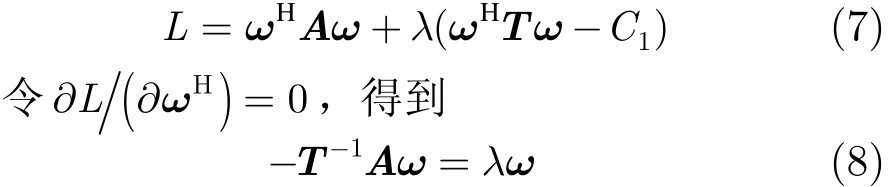
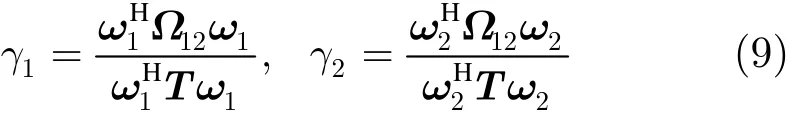
通常用相干区域边界来描述相干区域的形状。
4 改进的植被高度三阶段反演算法
4.1 三阶段反演算法
森林高度反演对研究生态系统循环有着重要意义,经典的森林高度三阶段反演算法基于RVoG模型,不同极化基下的相干系数γ(ω)在复平面(实部为自变量,虚部为因变量)上的分布为一条线段,复相干系数γ(ω)的表达式为:
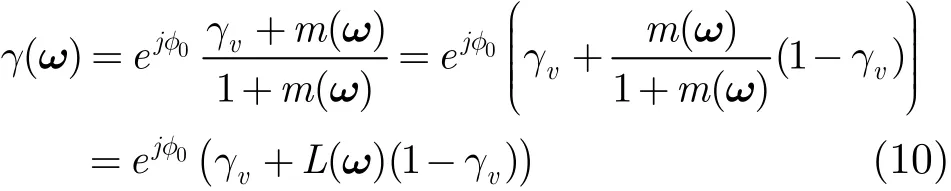
式中γv为体散射去相干,该线段称为可视线段,如图1所示。该线段所在直线与单位圆的交点中有一个点为地表相位点Q,可视线段中距离地表相位点最远的点定义为体散射相干系数点P。算法的3个步骤为直线拟合、地表相位估计、体散射去相干γv估计和建立查找表反演树高。理论上,应寻找使m(ω) = 0的点对应的相干系数作为体散射去相干的估计。但实际上一般假设在HV通道中 () 0mω= ,体相干系数的估计值为:
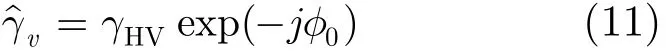
体散射去相干γv仅与植被高度hv及消光系数σ有关,如式(11)所示,建立查找表可以估计出植被高度hv。
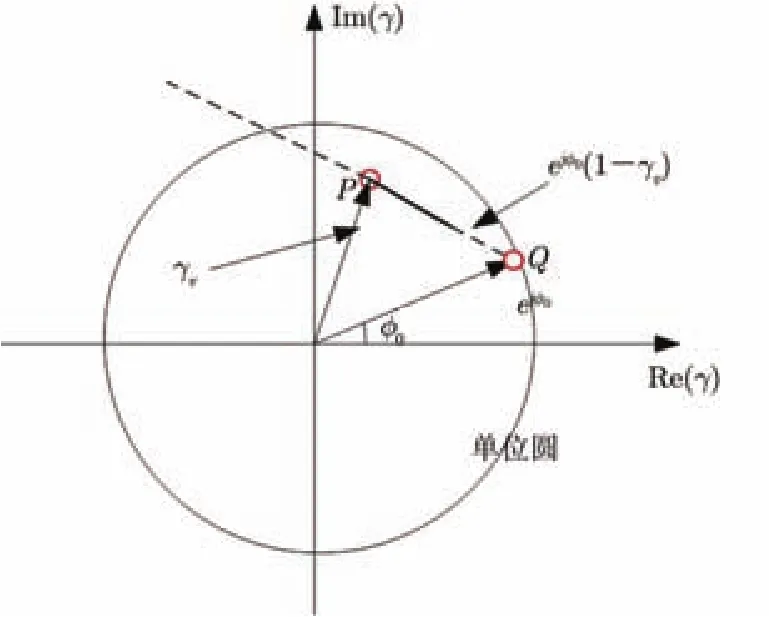
图1 传统三阶段反演算法原理示意图Fig. 1 The schematic of the traditional three-phase inversion algorithm
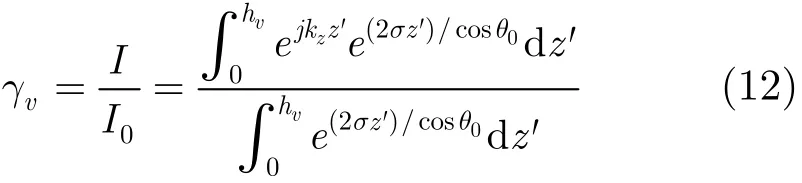
地表相位估计是三阶段反演的第1步,它的估计性能直接影响其它参数估计的准确性。在式(11)中,地表相位估计的误差直接影响体散射去相干的估计值。同时当体散射去相干估计误差也影响树高反演精度。
4.2 改进的三阶段反演算法
利用相干系数进行直线拟合的拟合误差会直接影响到地表相位估计精度,进而会影响树高反演结果,因此直线拟合是三阶段反演算法的基本步骤,必须降低拟合误差。传统的算法采用最小二乘法(LS)直线拟合法,存在只考虑自变量的缺陷。另外,传统算法假设 HV通道的相干系数γHV不包含地表散射成分,可将γHV近似为体散射相干系数;事实上,HV通道中还含有一定的地面散射分量,因此传统算法会造成森林高度的过低估计[10]。
本文利用TLS代替LS,因为TLS法同时考虑自变量与因变量中的误差,可以达到更高的拟合精度,进而可以反演得到更精确的地表相位精度;文中给出了TLS与LS直线拟合得到的地表相位的对比图。体散射相干系数理论上为拟合直线的可视线段上离地表相位点最远的点[2],这一点应该处在相干区域内,即必须存在一对极化矢量,使得相干系数的值满足该条件。若相干区域的线性度高,表明系统误差对相干系数的影响小,符合线性模型,则可把拟合直线与相干区域边界的两个交点中离地表相位最远的点定义为体散射相干系数值,如图2所示。若相干区域的线性度低,表明相干区域受系统误差影响大,则利用文献[4]提出的将相位最优相干点中离地表相位最远的点作为体散射点。具体步骤如下:
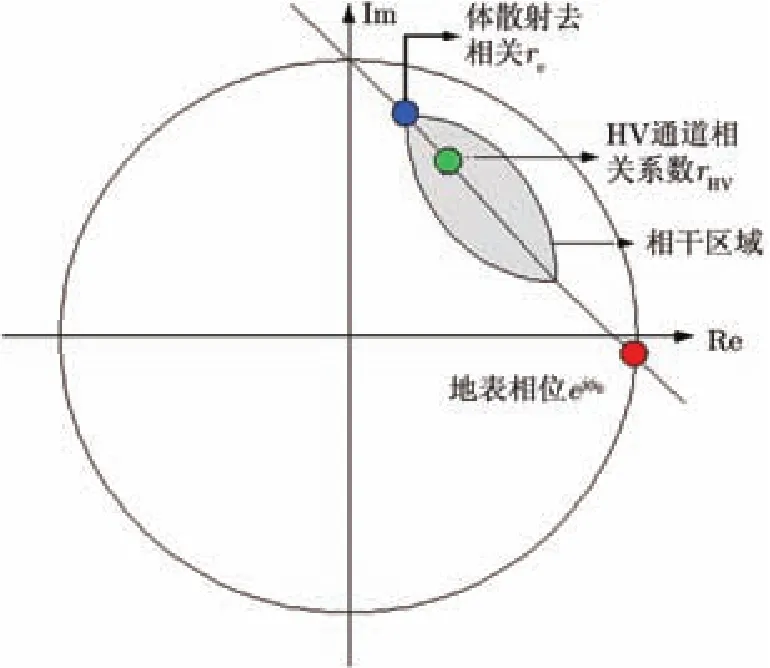
图2 体散射去相干估计示意图Fig. 2 The volume scattering decoherence estimation
(2) 根据文献[2]提出的三阶段反演算法中地表相位的计算方法可以得到地表相位,不在此赘述。
(3) 计算11个相干系数点分布的线性度量,可以用Gamma函数计算,如式(13)所示:
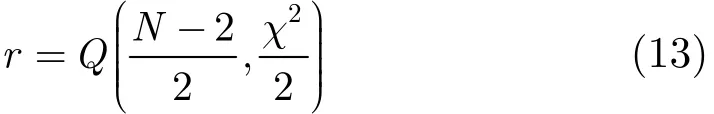
其中N为用于拟合直线的复相干点个数,2χ是各复相干点与拟合直线的绝对偏差的加权平均和,并根据相干系数点分布的线性度量设定置信度阈值,如
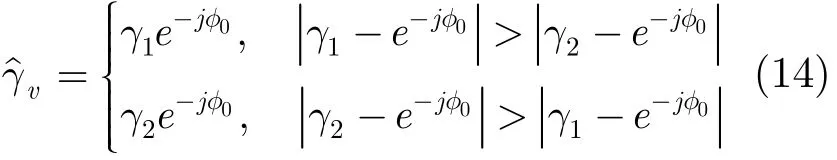
(5) 估计体散射相干系数后,建立查找表进行参数估计,可以得到更精确可靠的森林高度估计值。
5 仿真分析
采用由欧空局提供的PolSARpro软件产生一组L波段全极化干涉数据进行算法验证。仿真参数为:平台高度为3000 m,垂直基线为1 m,水平基线为10 m,入射角为45°,中心频率为1.3 GHz,树高为18 m,地表为平滑地表相位约为 0,图像大小为105×141。图3(a)所示的是本文选取的模拟极化干涉SAR数据Pauli基RGB彩色合成图,图3(b)中横线标注为方位向中心线,红色标注的点为位场景中心点,后文会对方位向中心线和场景中心点进行分析。
在图像中任取一个点,认为此时估计出的地表相位为正确值,将HV通道的相关系数作为体散射去相干系数,利用式(11)和式(12)得到原始树高反演值;保持其它参数值不变,引入固定的地表相位误差后得到存在误差时的体散射去相干和树高反演值,通过对比可分析地表相位对树高反演的影响。例如任取坐标为(25, 80)的点,原始树高反演的值为14.9 m,加入 0.1 rad地表相位误差时反演的值为14.1 m,误差为0.8 m;加入0.2 rad时反演的值为13.2 m,误差为1.7 m,可见很小的地表相位误差也会影响到树高估计精度。

图3 模拟数据Fig. 3 The simulated data
图4给出了利用TLS直线拟合方法得到的地表相位图,其中图 4(a)显示的是 LS的地表相位反演结果,图4(b)显示的是TLS算法地表相位反演结果。地表相位模拟时设为平滑地表相位约为0 rad,图4利用颜色表示地表相位,由蓝色到深红色表示地表相位由0 rad变化到2 rad。图4(c)所示为两种方法得到的地表相位统计直方图,地表相位的分布应该越靠近0越好。由图4可以看出TLS法直线拟合得到的地表相位更接近真实情况,因此可以获得更高的森林树高反演精度。
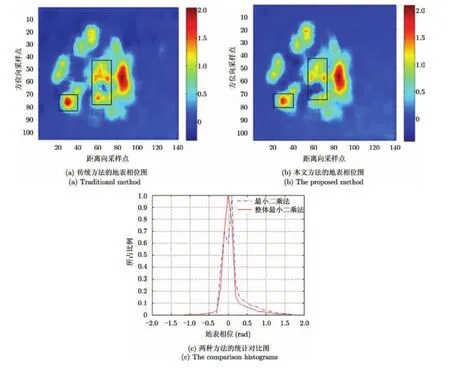
图4 地表相位反演结果Fig. 4 The inversion result of ground phase
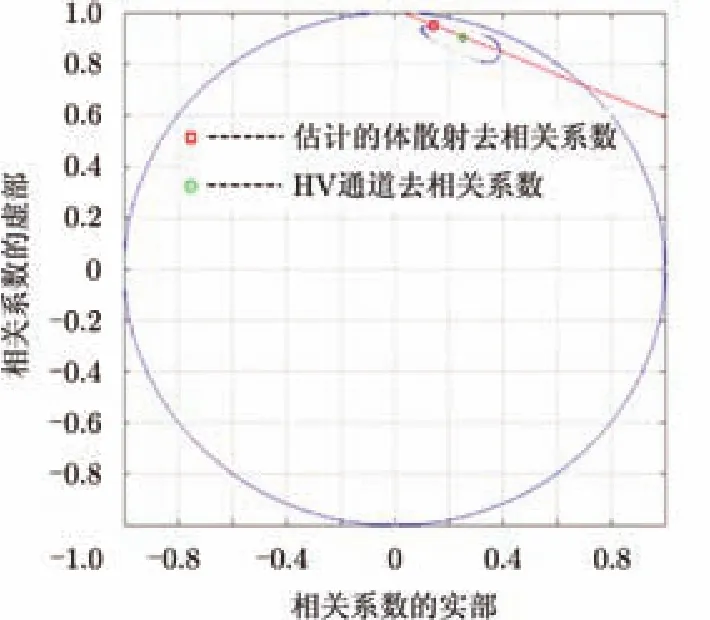
图5 拟合直线和相干区域以及两种方法得到的体散射相干系数Fig. 5 The fitting line, coherence shape, and the volume coherences using the two methods
图5所示是在场景中心点拟合出的相干直线、相干区域、以及本文算法估计出的体散射去相干系数和HV通道的相干系数。由图5可以看出,本文方法得到的体散射去相干系数的估计值比HV通道的相干系数值距离地表相位点更远。可以在一定程度上克服过低估计的问题。
图6给出了三阶段算法和本文算法反演出的森林高度估计结果,其中图 6(a)为传统三阶段方法的反演结果,图6(b)为本文算法反演结果,图6(c)为两种算法的树高反演统计的直方图对比图。
由图6可以看到,本文算法反演的树高值均匀分布在森林区域中,而在传统算法中反演的树高在森林区域中存在大量零值点,本文算法更接近真实情况。图 6(c)所示为整幅场景的树高反演直方图,实线和虚线分别表示本文反演方法和传统三阶段反演方法得到的整幅场景的树高反演直方图。由图6(c)可见,对于整幅场景,传统的三阶段反演算法造成树高过低估计,本文算法反演的树高直方图分布更接近理论高度18 m,由此可以说明本文的精确算法可靠有效。为了更有效的验证,本文选取图3(b)场景方位中心线的高度反演的结果进行更直观分析,如图7所示,其中实线表示本文方法反演出的树高,虚线表示传统三阶段方法反演出的树高,横线表示理论的树高。可以看出本文算法能在一定程度上克服传统反演算法植被高度被过低估计的问题,能提高反演精度。
为了更好地说明这个结果,本文对树高反演结果进行量化分析。表1列出了传统的三阶段反演算法和本文改进算法的树高反演平均误差和均方根误差的对比结果。通过定量对比可知,本文算法有效地提高了树高反演精度。
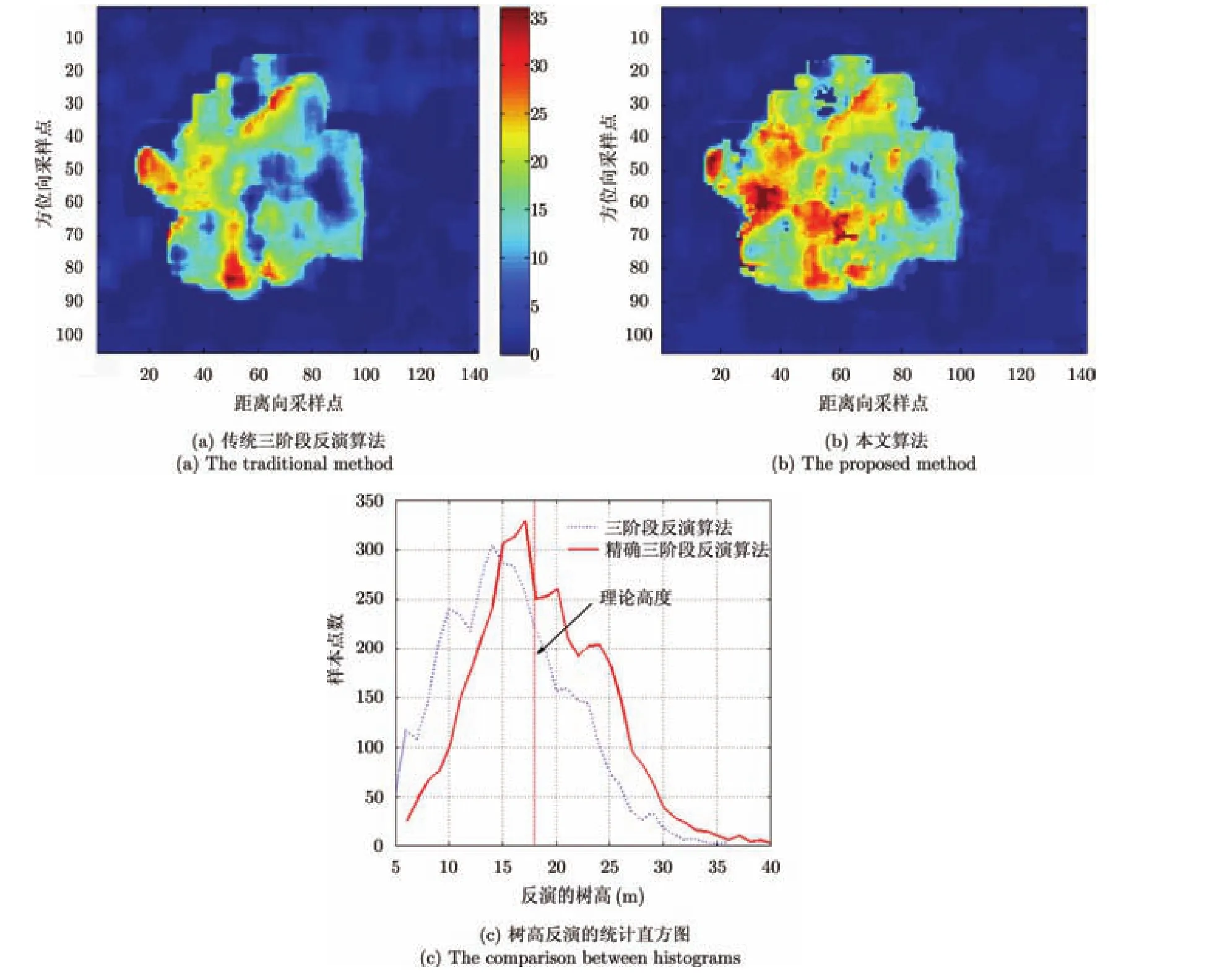
图6 树高反演结果Fig. 6 The inversion result of the forest height
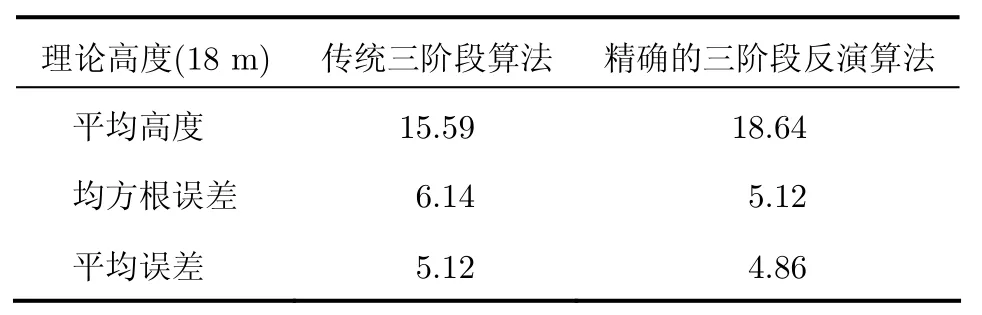
表1 两种算法的量化对比表(m)Tab. 1 The quantified comparison of the two methods
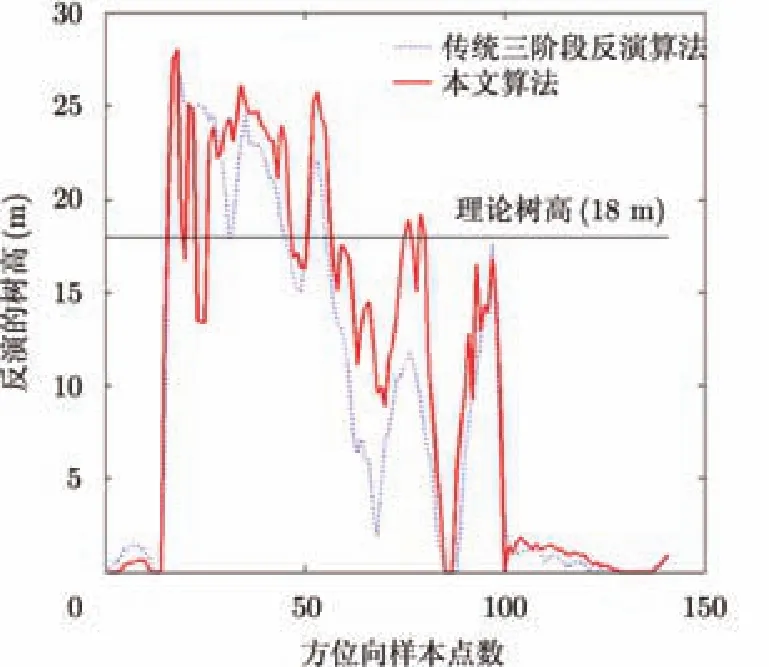
图7 方位中心线上反演的树高图Fig. 7 The inversed forest height in the azimuth center line
6 结束语
Cloude和Papathanassiou在RVoG模型的基础上根据相干系数的几何特性提出的三阶段树高反演算法在森林参数提取算法中取得了突破性进展,但是算法的每个步骤存在的误差会影响树高估计精度。其中直线拟合造成的地表相位估计误差和体散射去相干系数估计误差对树高反演精度的影响最为突出。本文利用整体最小二乘法进行直线拟合获得更精确的地表相位估计,针对体散去相干系数估计误差导致森林高度估计过低问题,本文利用Gamma函数作为线性度量自适应地提取法提取体散射相干系数,克服传统反演算法中估计不足的问题。通过仿真结果可以看到,本文算法的反演结果更加精确可靠。
[1] 吴一戎, 洪文, 王彦平. 极化干涉 SAR的研究现状与启示[J].电子与信息学报, 2007, 9(5): 1258-1262.
Wu Yi-rong, Hong Wen, and Wang Yan-ping. The current status and implications of polarimetric SAR interferometry [J].Journal of Electronics&Information Technology, 2007, 9(5): 1258-1262.
[2] Cloude S R and Papathanassiou K P. Three-stage inversion process for polarimetric SAR interferometry[J].IEE Proceedings-Radar,Sonar and Navigation, 2003, 150(3): 125-134.
[3] Tan Lu-lu, Zhang Jian-ming, Dai Da-hai,et al.. Improved three-stage inversion process for forest height inversion with PolInSAR data[C]. 2011 IEEE CIE International Conference on Radar, Chengdu, China, 2011: 1394-1397.
[4] 陈兵, 徐绍剑, 张平. 单基线PolInSAR反演算法研究[J]. 电子与信息学报, 2008, 30(7): 1744-1746.
Chen Bing, Xu Shao-jian, and Zhang Ping. Research on the single-baseline PolInSAR inversion algorithms[J].Journal of Electronics&Information Technology, 2008, 30(7): 1744-1746.
[5] 周广益, 熊涛, 张卫杰, 等. 基于极化干涉 SAR 数据的树高反演方法[J]. 清华大学学报(自然科学版), 2009, 49(4): 510-513.
Zhou Guang-yi, Xiong Tao, Zhang Wei-jie,et al.. Forestheight measurements based on polarimetric SAR interferometry[J].Journal of Tsinghua University(Science&Technology), 2009, 49(4): 510-513.
[6] 丁克良, 沈云中, 欧吉坤. 整体最小二乘法直线拟合[J]. 辽宁工程技术大学学报(自然科学版), 2010, 29(1): 44-47.
Ding Ke-liang, Sheng Yun-zhon, and Ou Ji-kun. Methods of line-fitting based on total least squares[J].Journal of Liaoning Technical University(Natural Science), 2010, 29(1): 44-47.
[7] Carlos L M and Papathanassiou K P. Cancellation of scattering mechanisms in PolInSAR: application to underlying topography estimation[J].IEEE Transactions on Geosience and Remote Sensing, 2013, 51(2): 953-965.
[8] Lee S K, Kugler F, Papathanassiou K P,et al.. Quantification of temporal decorrelation effects at L-band for polarimetric SAR interferometry applications[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(3): 1351-1367.
[9] 张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004: 408-413.
Zhang Xian-da. Matrix Analysis And Applications[M]. Beijing: Tsinghua University Press, 2004: 408-413.
[10] 孔建, 姚宜斌, 吴寒. 整体最小二乘的迭代解法[J]. 武汉大学学报(信息科学版), 2010, 35(6): 711-714.
Kong Jian, Yao Yi-bin, and Wu Han. Iterative method for total least-squares[J].Geomatics and Information Science of Wuhan University, 2010, 35(6): 711-714.
[11] Flynn T, Tabb M, and Carande R. Coherence region shape extraction for vegetation parameter estimation in Polarimetric SAR Interferometry[C]. International Geoscience and Remote Sensing Symposium, Toronto, Canada, 2002: 2596-2598.
[12] Chen Si-wei, Wang Xue-song, and Sato M. PolInSAR complex coherence estimation based on covariance matrix similarity test[J].IEEE Transactions on Geosience and Remote Sensing, 2012, 50(11): 4699-4710.

许丽颖(1987-),女,河北承德,博士生,研究方向为极化干涉与简洁极化干涉合成孔径雷达技术研究。
E-mail: xuliying3163@163.com

李世强(1967-),男,副研究员,硕士生导师,研究方向为星载 SAR系统设计与仿真/星载SAR成像新体制研究。
E-mail: lishq@mail.ie.ac.cn

邓云凯(1962-),男,研究员,博士生导师,研究方向为SAR系统设计与信号处理技术。
E-mail: ykdeng@mail.ie.ac.cn

王 宇(1980-),男,研究员,博士生导师,研究方向为SAR系统设计与信号处理技术。
E-mail: yuwang@mail.ie.ac.cn
Improved Three-stage Algorithm of Forest Height Retrieval with PolInSAR
Xu Li-ying①②Li Shi-qiang①Deng Yun-kai①Wang Yu①
①(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)
②(University of the Chinese Academy of Sciences, Beijing 100049, China)
Employing Polarimetric Interferometry Synthetic Aperture Radar (PolInSAR) data to inverse forest parameters is a hot topic in the research field of PolInSAR. The typical forest parameter inversion algorithm is the three-stage inversion algorithm based on Random Volume over Ground (RVoG) model. The errors of linear fitting and volume scattering correlation estimation are the major factors for parameter estimation accuracy. In this paper, straight line fitting employing the total least squares method is used to estimate the ground phase. Then, the Gamma function is applied as the line measure to adaptively estimate the volume scattering correlation. The improved three-stage inversion algorithm with PolInSAR is presented. The experiment result proves the forest parameters inversion result is accurate and reliable.
Polarimetric Interferometry SAR (PolInSAR); Total Least Squares (TLS); Forest height inversion; Random Volume over Ground (RVoG)
中国分类号:TN958
A
2095-283X(2014)01-0028-07
10.3724/SP.J.1300.2014.13089
2013-09-30收到,2014-01-21改回;2014-01-31网络优先出版国家自然科学基金(61072113)资助课题
*通信作者: 许丽颖 xuliying3163@163.com
