基于导航数据的Ka波段InSAR成像处理与分析

师 君 马 龙 韦顺军 时代奇 张晓玲 陈 刚

①(电子科技大学电子工程学院 成都 611731)

②(西安测绘研究所 西安 710054)

基于导航数据的Ka波段InSAR成像处理与分析

师 君*①马 龙①韦顺军①时代奇①张晓玲①陈 刚②

①(电子科技大学电子工程学院 成都 611731)

②(西安测绘研究所 西安 710054)

与其它波段相比，毫米波干涉SAR (InSAR)具有精度高、体积小的特点，是目前干涉SAR研究的重要方向之一。但由于较短的波长，其也给成像处理和干涉相位提取带来了一定困难。该文利用毫米波段干涉SAR数据，采用流结构后向投影(BP)算法结合IMU进行了毫米波SAR成像和干涉相位分析。研究发现，由于毫米波波长短，对天线相位中心变化更为敏感，为了保证系统的干涉相位，必须利用IMU数据进行精确的运动误差补偿。通过实测数据验证了采用各自计算天线相位中心的策略，后向投影算法可以在成像过程中精确补偿平地相位。

干涉SAR成像；成像性能分析；后向投影算法；基于导航数据的运动补偿

1 引言

与其它波段相比，Ka波段SAR穿透能力弱，能更好地反应积雪、植被等地貌的高程信息，且系统结构紧凑，重量轻。因此，近年来国外纷纷开展了Ka波段干涉SAR系统研制[1－5]。但另一方面，由于Ka波段波长更短，为了获得良好的干涉相位，需要系统具有较好的通道一致性且成像方法具有较好的相位保持能力。

对于机载 SAR系统，由于风场、湍流等因素的影响，天线相位中心轨迹较理想轨迹可能存在较大的偏差，严重影响SAR(特别是高波段SAR)图像质量，进而影响高精度DEM提取等SAR应用。由于传统的距离-多普勒(RD)算法、CS算法都基于SAR的多普勒质心、多普勒斜率模型，当IMU测量数据较为复杂时，上述方法需要较大改进才能实现对复杂运动误差的精确补偿。与之相比，后向投影(BP)算法[6－11]采用逐点匹配的处理方法，可实现IMU数据与成像处理的充分结合，更适合于复杂运动SAR成像处理。

本文基于实测Ka波段毫米波干涉SAR数据，对后向投影算法的在高分辨率 SAR成像以及干涉相位提取方面的性能进行了分析。第2节首先回顾了流结构BP算法的处理流程，并针对所处理数据由于距离向去斜率处理产生的存在的残留相位问题，对BP算法的补偿相位进行了修正。第3节从成像的角度出发，分析了实测数据的回波特征，IMU数据对成像结果的影响，以及去斜率处理对结果的影响。第4节从干涉相位的角度出发，对IMU数据、去斜率处理等对BP算法的保相性能进行了分析，并初步验证了地距投影条件下，BP算法所特有的去平地能力。

2 流结构后向投影算法

2.1 算法介绍

后向投影算法(BP)通过将回波数据逐点投影到图像空间各像素，实现各散射点能量的积累。与其它方法相比，BP方法成像原理简单，处理过程不存在任何近似误差，可适用于各种模式 SAR成像处理，且便于进行高精度运动误差补偿。BP算法工作示意图如图1所示。

一般地，BP算法包括如下步骤：

步骤1 确定图像空间

可以选择距离-方位向作为投影空间，以使得BP算法成像结果与其它算法成像结果兼容，也可以选择地面作为投影空间，以便于后续图像处理，像素间隔应略小于系统理论分辨率。

步骤2 距离压缩与插值

为了提高成像质量，需要对距离压缩后数据进行插值，可选择频域sinc插值。

步骤3 计算距离历史

给定某像素p，其距离历史为：

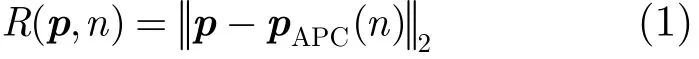
其中，pAPC(n)表示天线相位中心在第n个PRI的位置，表示向量2范数，n为慢时间域，p为散射点位置。

步骤4 计算回波位置

根据图1所示的雷达回波时序，某像素在第n个PRI对应的回波位置为：

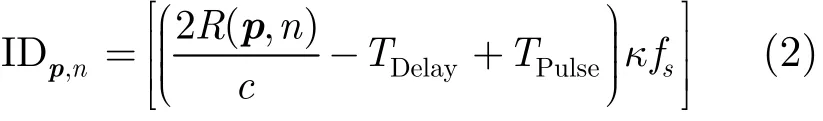
其中，[x]表示4舍5入取整，TDelay表示接收波门延时，c为光速，TPulse表示发射脉冲持续时间，κ表示频域插值倍数，fs表示采样频率。

步骤5 相参积累

补偿该散射点的多普勒相位，并将其投影到图像空间中，

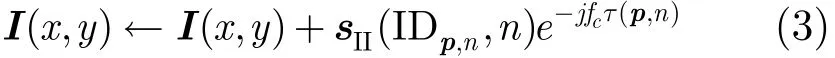
其中，fc为发射信号载频，I(x,y)表示图像空间，τ(n,p)为散射点到雷达的延时，“←”表示赋值操作。

步骤6 遍历所有像素和PRI

通过上述操作，即可实现对处理区域的成像处理。

2.2 去斜处理改进

由于目前实测数据距离压缩采用了去斜率处理技术，而去斜率处理会导致额外的方位向相位，因此在BP成像过程中，需要对残留相位进行补偿。假设系统发射线性调频信号，则单点目标回波可表示为：

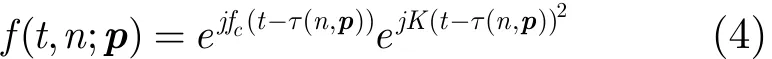
其中，t为快时间域，K为发射信号的调频斜率，

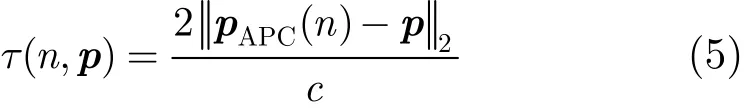
去斜处理将回波信号与发射信号共轭相乘，即：

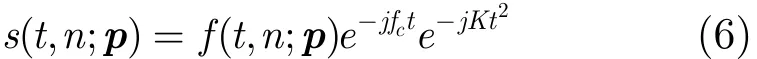
将线性调频信号相位的平方项展开，可以得到去载频和去斜率后的信号为：

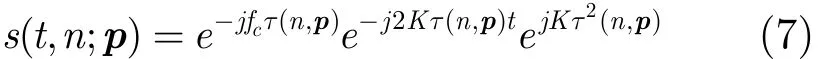
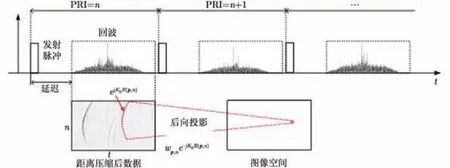
图1 BP算法工作示意图Fig. 1 Illustration on BP algorithm

式(7)中包含 3个复指数分量。第 1项为传统SAR系统的多普勒相位，产生方位向分辨率。第2项为快时间t的单频信号，且频率与目标的延时相关，因此，通过傅里叶变换即可实现对去斜率处理信号的距离压缩以及不同距离目标的分辨。去斜率处理距离向的分辨率由傅里叶变换的频率分辨率决定，并与发射信号的调频斜率和采样时间有关，两者乘积即为发射信号的带宽。因此，去斜率处理的距离向分辨率与脉冲压缩系统相同，ρR=c/(2B)。

式(7)中的第 3项为去斜率处理产生的残留相位，由于该项与快时间t无关，因此该项不会对距离压缩产生影响。但是另一方面，由于其与慢时间n有关，因此该项将会对系统的方位向处理产生影响，需要在相位补偿过程中加以补偿。此时，后向投影算法的相位补偿公式为：

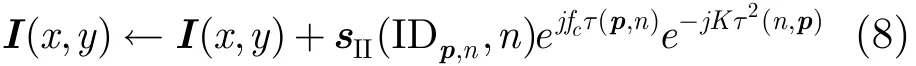
3 成像性能分析

为了获得较高的干涉相位，需要首先获得高精度的各通道 SAR图像，本节主要从信号特征，运动补偿和残留相位3个方面，分析后向投影算法的成像性能。

3.1信号分析

为了分析图像中强点目标的信号特征，首先根据天线相位中心轨迹，采用式(2)计算强点在距离压缩后数据中的位置，并逐一提取各位置处的复数据，如图2(a)所示，可以看出，计算所得ID(红色线段)与实测的强点回波良好吻合。

图2(b)为强点目标的方位向频谱，可以看出其表现出了 SAR方位向信号典型的带限信号特征。图2(c)为强点目标的时频谱，可以看出其表现出了SAR方位向信号典型的线性调频信号特征。图2(d)为强点目标的DCFT谱(Dechirp变换)，可以看出其与理想线性调频信号的DCFT谱类似，但并非精确的十字结构，表明该强点可能并非严格意义上的单点目标。

3.2 IMU数据分析

假设 SAR系统天线相位中心实际轨迹为，给定散射点p，回波对应的实际距离历史为：

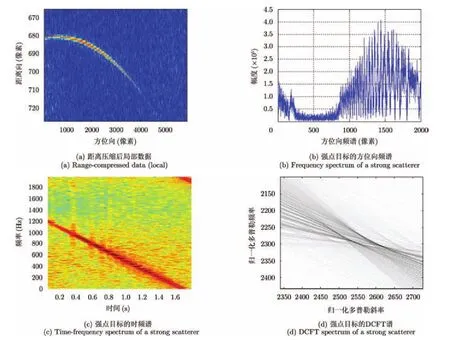
图2 Ka波段SAR强点目标的回波特征Fig. 2 Signal characteristics of Ka-band SAR data

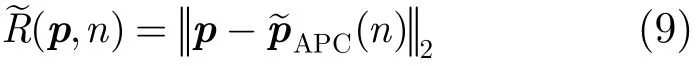
在实际轨迹未知的条件下，成像过程往往假设平台直线运动。此时，用于补偿的距离历史为：

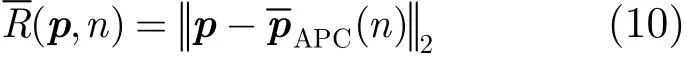
和之间的误差即为运动误差，其导致两方面的影响：在补偿距离走动效应时，计算ID可能存在偏差，导致遗漏散射点的部分回波，并进入了额外的噪声数据；在计算补偿相位时出现误差，导致无法完全补偿散射点的多普勒相位，影响图像聚焦和干涉相位精度。其中，第1类误差对距离历史精度要求为距离分辨率级，一般为分米级；第2类误差对距离历史精度要求为亚波长级，一般需要达到毫米级。

为了进一步分析，可以对式(9)和式(10)做差，得到距离历史误差近似公式为：

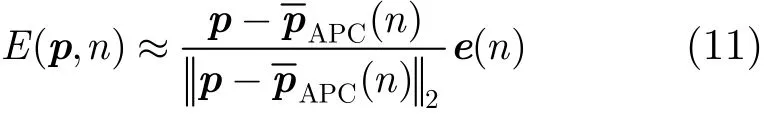
其中，e(n)为天线相位中心实际轨迹与直线近似轨迹之差。

式(11)的第1项为平台到散射点的方向矢量，式(11)的物理意义十分清晰，即距离误差为天线相位中心轨迹误差沿距离向的投影。按照合成孔径雷达理论，为了实现精确成像，相位误差应控制在波长的1/8以内，对于Ka波段，距离误差应小于0.5 mm。图3为IMU测量得到的实际误差。可以看出，平台较直线轨迹的偏移量达到了至少分米量级。

因此，必须利用 IMU测量数据进行补偿。相应地，根据SAR相位补偿对误差要求，IMU测量精度也应达到毫米量级。需要说明的是，1/8的相位误差条件基于随机噪声相位模型。针对 IMU测量系统，需要保证预处理后(滤波、拟合等)的天线相位中心轨迹足够光滑，随机抖动小于1 mm。对于 IMU测量单元的随机游走类偏差以及卡尔曼滤波导致的偏差，仍需要进一步根据误差类型加以分析。保守地说，上述误差在一个孔径时间内的积累应小于1 mm(此时，上述误差可以完全忽略不计，但误差如果大于1 mm，还需要根据误差的时间特性(线性特征、高阶特征、随机特征)加以进一步分析与讨论。

图4(a)和图5(a)为采用平均速度进行BP成像的结果(载频约为35 GHz，信号带宽约1 GHz，平台速度约60 m/s，作用距离约1200 m，入射角约45°，场景大小8192像素×8192像素，距离向像素间隔0.10 m，方位向像素间隔0.05 m)，可以看出，虽然图像实现的聚焦，但是整幅图像的对比度较低，强点目标在图像中存在较为明显的散焦，且图中的道路等目标轮廓较为模糊。

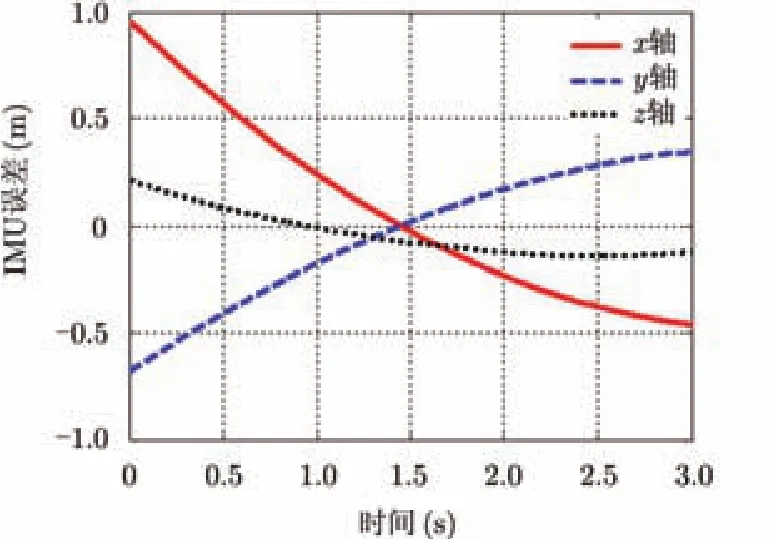
图3 航迹高阶误差Fig. 3 High-order trajectory errors

图4 整体效果对比Fig. 4 Comparison on the whole image

图4(b)和图5(b)为利用IMU数据进行非匀速运动误差补偿后的成像结果，可以看出，此时图像的对比度更大，局部区域的道路轮廓更为明显，且强点目标散焦现象较图5(b)大大减弱，但存在一定程度的散焦。

3.3 去斜率影响分析

由于目前阶段的系统在距离向采用了去斜率处理技术，导致图像在方位向存在一定的残留相位，可能会影响最终成像质量。因此，本节对残留相位的影响进行了分析。

图6为利用式(7)得到的多普勒分量和残留相位分量产生的方位向信号频谱。从中可以看出，多普勒分量导致的方位向频谱有大约1200 Hz，而由于残留相位产生的方位向频谱只有大约3 Hz左右。因此，多普勒分量在目前系统的方位向分辨率中占主要贡献，残留相位的影响较小。

图7为补偿残留相位后得到的BP成像结果，可以看出，补偿残留相位对图像整体效果影响不大。但对比局部图可以发现，补偿残留相位后图像的对比度要略微优于未补偿图像。

图8为补偿残留相位前后某强点目标成像效果比较，可以看出，目前成像处理对于强点目标仍存在一定的残留距离走动和方位向散焦，其可能原因首先是目前图像像素间隔很密(0.10 m×0.05 m)，对系统参数、运动误差补偿的要求较高，可能存在参数估计不准的问题。对比补偿残留相位前后的图像，可以发现，未补偿残留相位时，该强点散焦能量向左侧偏移，而补偿残留相位后，强点散焦能量较为对称。因此，在干涉处理中目前选择补偿残留相位后图像进行分析(研究过程中对两种补偿方法的干涉相位进行了分析，发现是否补偿该相位对两幅图像的相参性及残差点数目影响不大)。

4 相位性能分析

本节利用Ka波段干涉SAR的两幅图像对目前BP成像算法的相位特性进行分析。

4.1 BP算法的去平地能力

图5 局部区域对比Fig. 5 Comparison on the local region

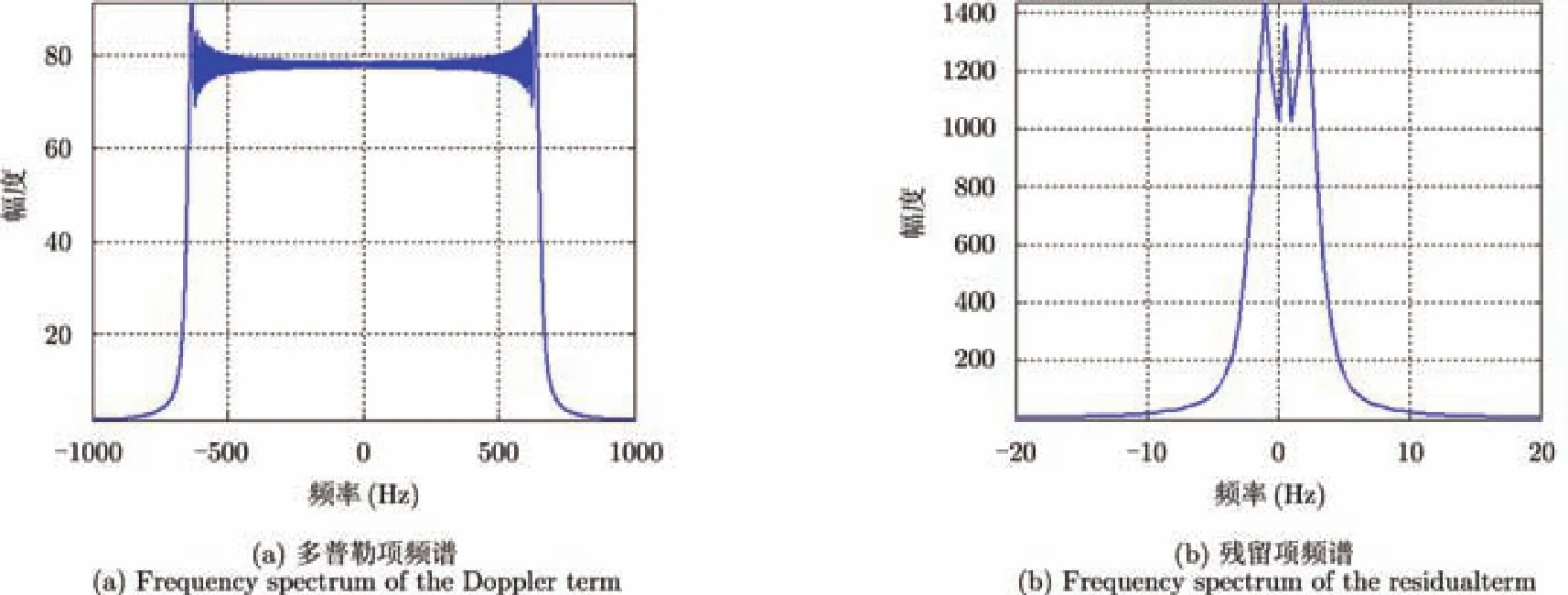
图6多普勒相位与残留相位方位向频谱Fig. 6 Frequency spectrums of the Doppler term and residualterm

传统的SAR成像算法基于多普勒质心和多普勒斜率模型，即通过补偿距离历史的1阶分量、2阶分量及高阶分量实现对散射点的能量聚集。由于实际距离历史的 0阶分量被保留，因此干涉相位为主、辅天线到散射点最短距离(理想正侧视条件下)之差。

图7 补偿残留相位后BP成像结果Fig. 7 Imaging result after compensating the residual phase

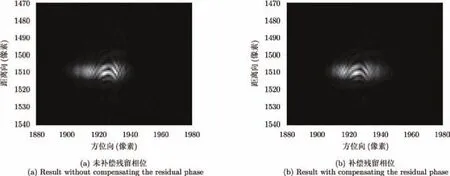
图8 补偿残留相位前后成像结果对比Fig. 8 Comparison on the imaging results with and without the residual phase

而对于BP算法，由于采用精确距离历史进行相位补偿，因此，用于进行干涉处理的0阶分量也在成像过程中剔除。为了保证BP算法与其它算法兼容，最简单的方法是在补偿干涉相位时保留距离历史的0阶相位、此时，补偿相位为(此处忽略由于去斜率引入的残留相位，并将相位表示为波数的形式)：

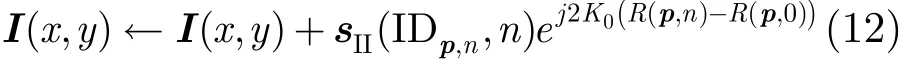
其中，K0为载波波数，R(p,0)表示中心时刻的斜距。

当忽略平台的姿态误差时，主天线的距离历史可以近似认为与辅天线的距离历史平行。此时，主天线BP与辅天线BP具有相同的多普勒斜率及高阶项。采用标准的BP算法(不减去0阶项)，利用主天线的参数可以实现辅天线通道成像处理。

观察式(12)可以发现，由于在成像过程中都减去了主天线的0阶分量(注意，如果主辅天线利用各自参数进行成像处理，则是减去各自天线的0阶分量)。该过程相当于利用式(12)进行成像处理后，在主辅天线上各乘了一个相同的相位。由于干涉相位提取时需要对主辅图像相位做差，相同的常数相位不会对成像过程产生影响。

因此，忽略主辅天线相位中心的位置差别，只利用主天线的参数对两幅图像进行成像处理得到的干涉相位与其它成像处理算法得到的干涉相位相同。同样地，此时BP算法也存在由于基线因素导致的图像偏移，需要在干涉相位提取中采用图像配准、去平地等技术进行补偿。

为了进一步提高成像处理精度，需要在处理过程中考虑姿态误差，此时主辅天线相位中心轨迹不再平行，无法统一利用主天线进行成像处理，而需要利用主辅天线各自参数分别成像。

为了得到与传统干涉 SAR一致的相位，则需要补偿的主辅天线相位项分别为：

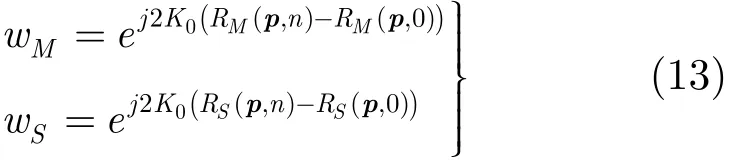
其中，M,S分别代表主天线和辅天线。如果不补偿0阶项，则干涉相位为：

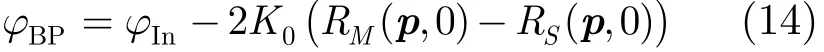
其中，ϕIn表示式(13)对应的理想的干涉SAR相位，ϕBP表示标准 BP算法分别用主辅天线参数成像得到的干涉相位。

观察最后一项可以发现，ϕIn和ϕBP之间相差的相位为假设散射点位于像素点时(一般情况下，散射点位于3维地理空间，像素点位于2维图像空间，散射点被“映射”到像素点，而非实际“位于”像素点)的干涉相位。由于像素点的高度为 0(选择水平面作为BP算法投影面)，所以该相位实际上是像素点位置的平地相位。

因此，通过在成像处理过程中精确计算主天线和辅天线的天线相位中心历史，并利用各自参数进行成像处理，可以剔除干涉相位中的平地相位。另外，BP算法的投影特性还可以补偿部分的主辅图像间的位置偏差，但无法补偿由于高程导致的主副图像像素偏移(由于散射点高度未知)。

4.2 实测数据分析

图 9为采用上述两种策略得到的干涉相位结果比较。图9(a)为只利用主天线进行双通道数据成像得到的干涉相位图(两幅图的相参性为 0.9174 (未剔除遮挡区域像素点)，残差占整幅图比例8.865%)，可以看出，此时图像存在明显的平地相位，需要进行相应的去平地处理。图9(b)为精确计算各自天线相位中心，并进行补偿，得到的干涉相位图(两幅图的相参性为 0.9156，残差占整幅图比例9.110%)。可以看出，此时干涉图中的平地相位并不显著，可以直接进行滤波、解缠等后续处理。图9(c)为图9(b)滤波后的干涉相位图，能反映出典型的地形特征。

图 10为图 9(c)局部区域的干涉相位图和对应的3维效果图(目前处理未包含相位解缠操作)，从中可以看出，对于A区域，干涉相位图中存在显著的条状纹理特征，能反映出实际地面上的规则高低起伏，对于B区域，干涉相位图中存在显著的块状纹理特征，也反映出实际地面上的规则高低起伏。

5 结论

通过对实测毫米波InSAR数据分析，可以看出：

(1) 目前的毫米波InSAR具有较好的相参性，能够得到较高精度的干涉相位。

(2) 由于毫米波波长短，对天线相位中心变化更为敏感，为了保证系统的干涉相位，必须利用IMU数据进行精确的运动误差补偿。

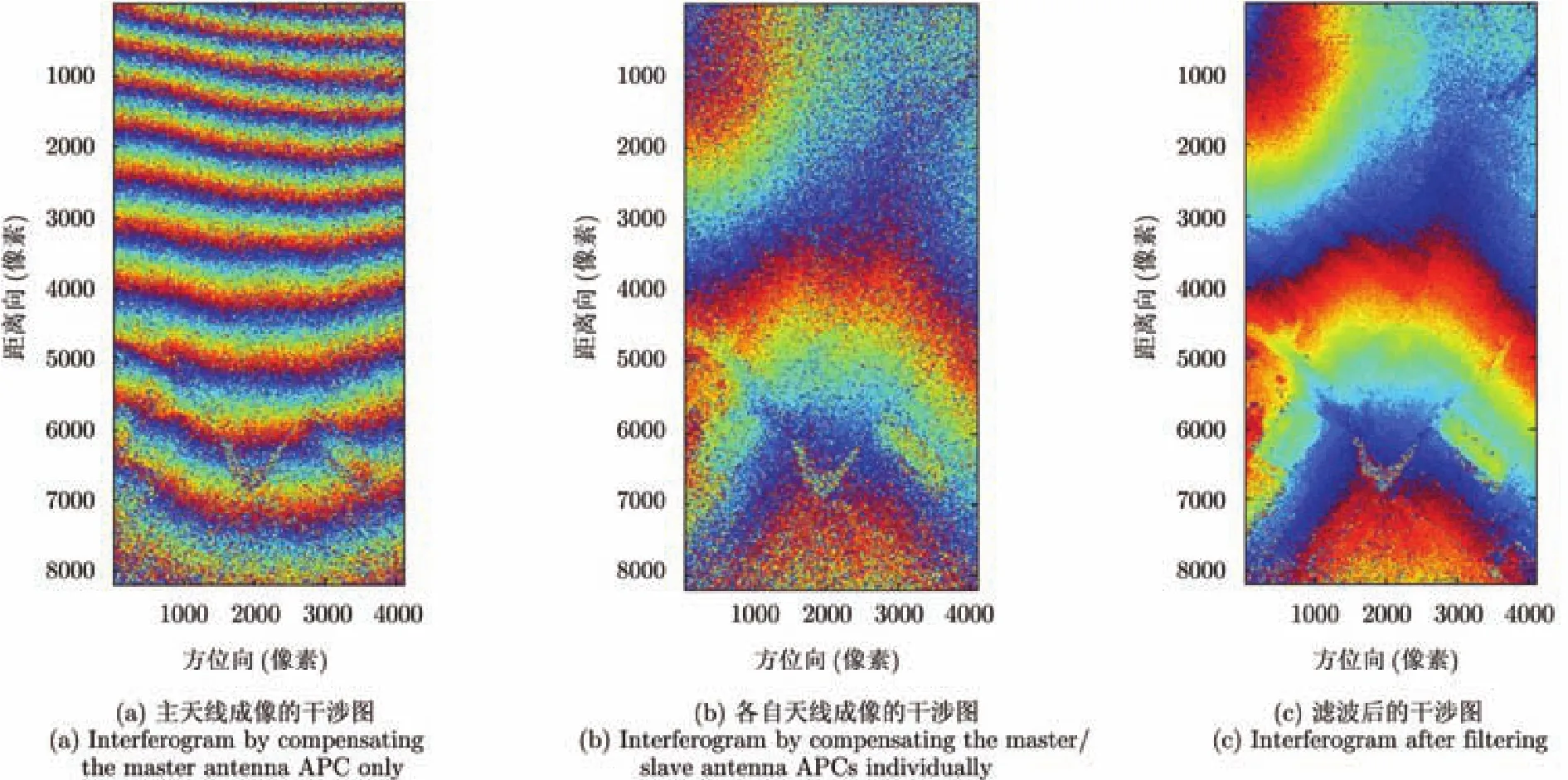
图9 BP算法得到的干涉相位图(方位向隔一抽取，保证整幅图像0.1 m×0.1 m比例)Fig. 9 Interferograms by using BP algorithm (down-sampling (base-2) in the azimuthdirection to ensure 0.1 m×0.1 m scale)

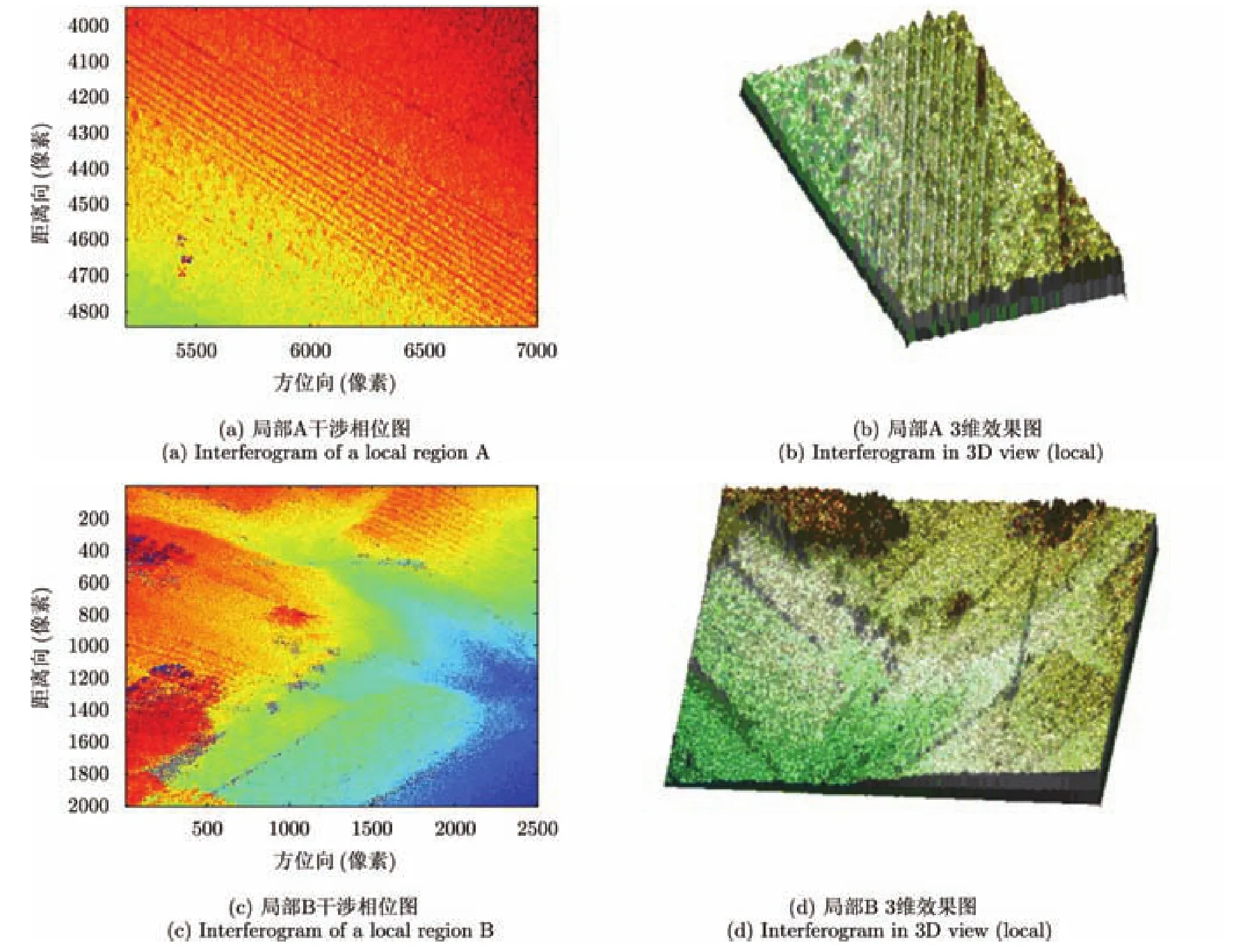
图10 局部干涉相位图Fig. 10 Interferograms of local regions

(3) 通过实测数据，验证了采用各自计算天线相位中心的策略可以在成像过程中精确补偿平地相位。

(4) 从干涉相位也可以看出，目前的干涉相位图仍存在较大的噪声，其可能由于未进行精确图像配准、未进行精确运动误差补偿等因素引起。因此需要进一步开展深入研究。

致谢感谢中航科工二院23所提供研究所需的Ka波段干涉SAR数据。

[1] D’Addio S and Ludwig M. Modeling analysis of rain effect on Ka-band single pass InSAR performance[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS2009), Cape Town, Republic of South Africa 2009, 4: 913-916.

[2] Ludwig M, D’Addio S, and Engel K. A spaceborne Ka-band SAR interferometer concept based on scan-on-receive techniques[C]. 2010 8th European Conference on Synthetic Aperture Radar (EUSAR), Berlin, Germany, 2010: 1-4.

[3] Schmitt M and Stilla U. Adaptive multilooking of airborne Ka-band multi-baseline InSAR data of urban areas[C]. 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 2012: 7401-7404.

[4] Schaefer C and Lopez-Dekker P. Interferometric Ka-band SAR with DBF capability[C]. 2012 9th European Conference on Synthetic Aperture Radar, Nuremberg, Germany, 2012: 7-10 .

[5] Mokadem A, Thirion-Lefevre L, and Colin-Koeniguer E. Analysing urban areas in the frame of non-line of sight target detection electromagnetic modelling, validation and application to real data in Ka-band[C]. 2013 IEEE International Conference on Electromagnetics in Advanced Applications (ICEAA), Torino, Italy, 2013: 543-546.

[6] Peters T M. Algorithms for fast back- and re-projection in computed tomography[J].IEEE Transactions on Nuclear Science, 1981, 28(4): 3641-3647.

[7] Ulander L M H, Hellsten H, and Stenstrom G. Synthetic-aperture radar processing using fast factorized back-projection[J].IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(3): 760-776.

[8] Cantalloube H and Dubois-Fernandez P. Airborne X-band SAR imaging with 10 cm resolution: technical challenge and preliminary results[J].IEE Proceeding-Radar,Sonar and Navigation, 2006, 153(2): 163-176.

[9] Ash J N. An Autofocus method for backprojection imagery in synthetic aperture radar[J].IEEE Geoscience and Remote Sensing Letters, 2012, 9(4): 104-108.

[10] Tan Wei-xian, Li Dao-jing, and Hong Wen. Airborne spotlight SAR imaging with super high resolution based on backprojection and autofocus algorithm[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS2008), Boston, Massachusetts, USA, 2008, 4: 1300-1303.

[11] Shi Jun, Ma Long, and Zhang Xiao-ling. Streaming BP for non-linear motion compensation SAR imaging based on GPU[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(4): 2035-2050.

师 君(1979-)，男，河南人，获电子科技大学工学博士学位，目前为电子科技大学副教授，主要从事SAR数据处理方面研究。

E-mail: shijun@uestc.edu.cn

马 龙(1990-)，男，安徽人，获电子科技大学学士学位，目前在电子科技大学攻读硕士学位，主要从事SAR成像技术研究。

E-mail: 1057616261@qq.com

韦顺军(1983-)，男，广西人，获电子科技大学工学博士学位，目前为电子科技大学讲师，主要从事SAR成像技术、干涉SAR技术研究。

E-mail: 249785144@qq.com

时代奇(1988-)，男，河北人，获电子科技大学学士学位，目前在电子科技大学攻读硕士学位，主要从事干涉SAR成像技术研究。

E-mail: 654729253@qq.com

张晓玲(1964-)，女，四川人，获电子科技大学工学博士学位，目前为电子科技大学教授/博导，主要从事 SAR成像技术、雷达探测技术研究。

E-mail: xlzhang@uestc.edu.cn

陈 刚(1976-)，男，陕西人，获国防科技大学工学硕士学位，目前为西安测绘研究所副研究院/副主任，主要从事InSAR数据处理、干涉定标技术研究。

E-mail: splitter@263.net

Ka-band InSAR Imaging and Analysis Based on IMU Data

Shi Jun①Ma Long①Wei Shun-jun①Shi Dai-qi①Zhang Xiao-ling①Chen Gang②

①(School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)
②(Xi’an Research Institute of Surveying and Mapping, Xi’an 710054, China)

Compared with other bands, the millimeter wave Interferometric Synthetic Aperture Radar (InSAR) has high accuracy and small size, which is a hot topic in InSAR research. On the other hand, shorter wavelength causes difficulties in 2D imaging and interferometric phase extraction. In this study, the imaging and phase performance of the streaming Back Projection (BP) method combined with IMU data are analyzed and discussed on the basis of actual Ka-band InSAR data. It is found that because the wavelength of the Ka-band is short, it is more sensitive to the antenna phase-center history. To ensure the phase-preserving capacity, the IMU data must be used with accurate motion error compensation. Furthermore, during data processing, we verify the flat-earth-removing capacity of the BP algorithm that calculates and compensates the master and slave antenna phase centers individually.

InSAR imaging; Imaging performance analysis; Back Projection (BP) algorithm; Motion compensation based on IMU data

中国分类号：TN957.52

A

2095-283X(2014)01-0019-09

10.3724/SP.J.1300.2014.13142

2013-12-24收到，2014-02-21改回；2014-03-06网络优先出版

61101170)，博士后基金(2011018511001)和高分专项(GFZX04031102)资助课题

*通信作者： 师君 shijun@uestc.edu.cn