基于高频渐近方法的导弹目标群动态RCS仿真

2014-08-05董纯柱任红梅殷红成

雷达学报 2014年2期

关键词：诱饵弹头插值

赵涛董纯柱任红梅殷红成

①(中国传媒大学信息工程学院北京 100024)

②(电磁散射重点实验室北京 100854)

基于高频渐近方法的导弹目标群动态RCS仿真

赵涛*①②董纯柱①②任红梅②殷红成①②

①(中国传媒大学信息工程学院北京 100024)

②(电磁散射重点实验室北京 100854)

针对导弹目标群的动态RCS仿真问题，该文提出一种基于高频渐近理论的高效预估方法。该方法基于最小能量弹道仿真得到弹头、诱饵和助推级等群目标的弹道，在测量雷达坐标系下解算得到各时刻目标的位置和姿态，建立分离过程的目标群动态场景，并利用物理光学法(PO)、等效边缘流法(EEC)和射线弹跳法(SBR)计算目标群的镜面反射、边缘绕射和多次反射贡献获得动态RCS数据。与采用静态全极化数据的常规插值方法获取的RCS数据对比分析表明，在场景中各目标距离较远且无相互遮挡时，两者吻合；当目标群密集分布存在相互遮挡时，插值方法实现难度大大增加，而该文方法仍能快速得到有效的结果。

雷达信号处理；导弹目标群；复杂场景；电磁散射；RCS

1 引言

导弹目标在沿弹道飞行过程中将释放或分离多种不同类型的目标，构成了密集目标群[1]，通常包括轻诱饵、重诱饵和助推级等，这些目标以近乎相同的速度伴随飞行，并具有相似的弹道特性，增加了导弹防御系统跟踪和识别的时间，显著提高了弹头生存能力，亦大大增加了弹头目标检测、跟踪和识别的难度。为了满足弹道目标检测和识别研究对海量电磁散射特性数据的要求，亟需开展弹道目标群动态RCS仿真方法研究。

目前，复杂目标动态RCS仿真方法主要有基于散射点模型的近似模拟方法和基于测量或理论仿真静态数据的插值拟合方法两种。前者将复杂目标等效成多个孤立的理想点散射中心，并假定目标的散射场由这些散射点贡献相干叠加而成，该方法实现简单，但无法准确考虑散射中心因频率、极化和相互遮挡关系等变化引起的散射特性差异，对复杂目标的模拟结果与真实情况存在较大偏差。后者首先通过测量或理论仿真得到复杂目标全空间静态RCS数据，然后根据目标-雷达之间的姿态角和极化变换关系插值生成目标的RCS数据。考虑到复杂目标RCS随姿态角(方位角和俯仰角)变化的敏感性，这种方法通常需要以很小的姿态角间隔(如0.1°)建立目标的全空间RCS数据集，测量和仿真的工作量巨大，并且不可避免地存在插值误差，因而限制了其工程应用范围。随着电磁散射计算技术的快速发展，基于电磁散射建模的复杂目标动态RCS仿真成为可能。电磁散射建模的数值方法，如矩量法(Method of Moment,MoM)[2]等，虽然精度高，但受计算时间和内存的限制，很难满足超电大尺寸目标群以及海量计算等对计算效率的要求。以物理光学法(PO)、等效边缘流法(EEC)、射线弹跳法(SBR)等为代表的高频渐近方法[3－5]在保证较高计算精度的同时效率极高，在(超)电大复杂目标动态回波场景仿真中具有显著优势。

针对典型目标的动态RCS或回波仿真，国内外已经有很多学者开展了研究。文献[6-8]基于点散射模型仿真了球头锥等目标不同运动形式下的动态RCS，受其模型精度的影响不能准确反映真实目标的散射特性；文献[9,10]利用典型弹头的全方位暗室测量数据，按弹头与雷达视线之间的角度变化关系抽取测量数据获得动态RCS，该方法不可避免地存在插值误差且测量的工作量巨大；文献[11-14]基于全波数值建模或高频散射建模方法获得了单个目标在高速运动或微动下的动态RCS或宽带回波。针对弹道中段分离过程导弹目标群的动态RCS仿真，既要考虑各目标之间的相互遮挡等因素以保证计算的准确性，又要尽量保证仿真方法通用、高效，目前尚未见国内外文献有相关报道。为此，本文提出一种高效仿真方法，基于最小能量弹道方法仿真得到弹头、诱饵和助推级等目标群的弹道，在北天东雷达坐标系下解算得到各时刻目标群的位置和姿态，建立分离过程的目标群动态场景，采用快速射线追踪技术完成对动态场景的实时消隐运算和耦合路径追踪，并利用PO+EEC+SBR计算各个飞行时刻来自目标群的镜面反射、边缘绕射和耦合散射贡献，快速预估导弹目标群动态RCS数据。以带尾翼的弹头和末级助推及轻、重诱饵组成的复杂场景为例，对本文方法的有效性和通用性进行了验证。

2 目标群动态RCS仿真方法

首先设定导弹的关机点参数以及诱饵、助推与导弹分离时刻的速度、轨道倾角等信息，基于最小能量弹道[15]方法求解开普勒方程得到各目标在任一时刻的偏近点角和运动参数，仿真计算目标群在测量雷达坐标系下各时刻的3维空间位置、方位、俯仰和横滚角，并导入目标群各目标的3维几何和材料模型，生成各时刻的动态场景数据；其次，通过设定入射方向、入射波频率和极化等参数，采用快速射线追踪技术完成对动态场景的快速消隐运算和耦合路径追踪，并基于PO+EEC+SBR计算来自目标群的镜面反射、边缘绕射和耦合散射贡献，相干叠加得到目标群的散射总场；最后对散射总场进行极化接收获得目标群的RCS。

采用本文方法仿真目标群动态RCS的过程如图1所示。

2.1 镜面反射计算

在高频条件下，PO用散射体表面的感应电流取代散射体本身作为散射场的源，然后对散射体的表面感应电流积分而求得散射场。在平面波入射情况下，略去时谐因子ejω t，根据Stratton-Chu方程，物体表面远区散射场的一般计算公式[3,16]为：

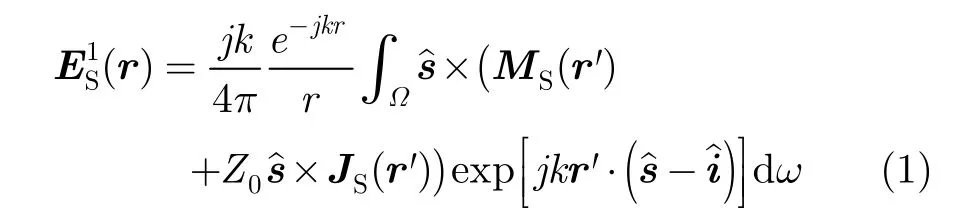
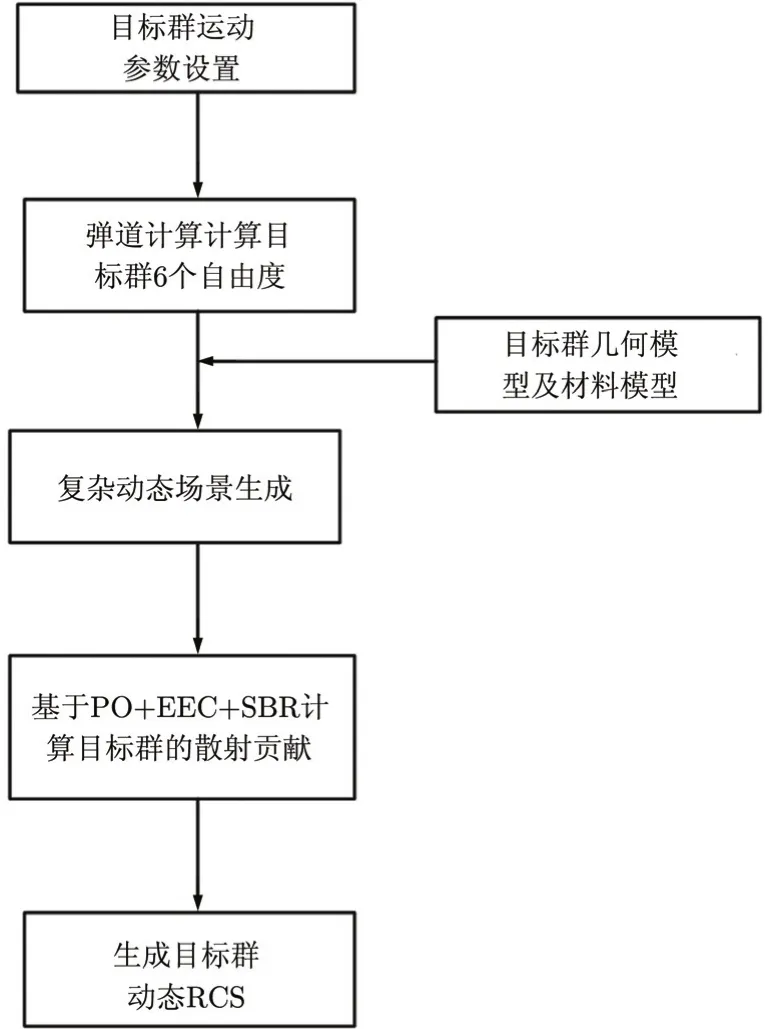
图1 目标群动态RCS仿真流程Fig. 1 The simulation procedure of dynamic RCS for target group

图2 目标表面的电磁散射Fig. 2 Electromagnetic scattering of target surface

Ω上电磁流的矢量幅度，其中的相位因子已经被分离出来，并包含在被积函数的指数项中。JS(r')和MS(r')可以根据两个基本物理光学假定利用等效原理获得

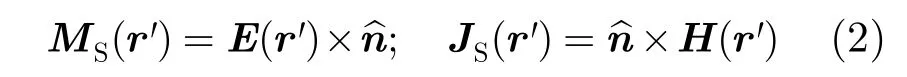
其中，E(r')和H(r')是目标表面上照明部分的总电场和总磁场。在物理光学近似的条件下，目标表面的总场可以认为是入射场和反射场之和。当目标采用平面三角面元表示时，目标散射场的积分可以采用Gordon的方法进一步简化[17]。

2.2 边缘绕射计算

根据Michaeli的等效电磁流的概念，对边缘为C的任意劈，它的远区边缘绕射场可表示为：

2.3 多次反射计算

射线弹跳法在计算目标自身或目标-目标间的耦合散射时主要包括射线追踪、幅度跟踪和口面积分3个主要步骤：

(1)射线追踪

对于采用平面元拟合的复杂目标群，可以将入射平面波分解为一组组密集的平行射线从源点(发射雷达处)沿入射方向发射，入射线与目标面元的交点以及各次反射的方向可以由快速射线自动追踪算法[5]确定，追踪过程如图3所示。射线追踪完毕后，可以获得对应每一条入射线的一组目标内的反射点(包括射线与口面的交点)和射线离开目标时的出射方向。

(2)幅度跟踪

通过快速射线追踪算法找到目标体内的射线路径之后，射线上的电场矢量可以通过下列递推关系确定[19]：

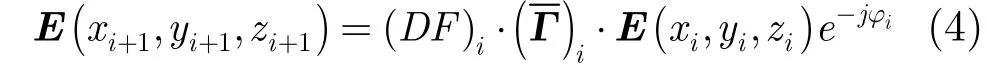
(3)口面积分

在给定口径面Σ上，由于射线管i的顶点位置和几何光学场(Eap,Hap)已经由射线追踪和幅度追踪确定，其远区散射场表达式为：

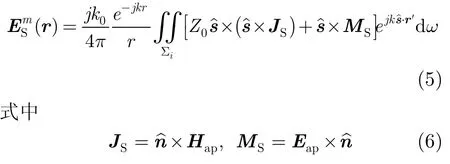
其中，k0为入射波波数，ŝ为接收方向上的单位矢量，Σi为射线管i在口径面Σ上的投影面，nˆ为Σi的单位外法矢量。目标群总的多次反射贡献是上述各个射线管散射贡献之和。

2.4 动态RCS计算

由弹道计算仿真各时刻各目标的6个自由度，并导入各目标的几何和材料模型，建立在雷达坐标系下的复杂动态场景。假定雷达默认跟踪弹头为主目标，以弹头的几何中心为跟踪中心，由此确定入射波方向和电场极化矢量，计算复杂场景目标群的镜面反射、边缘绕射和多次反射贡献，最后对散射总场进行极化接收获得目标群的全极化动态RCS。

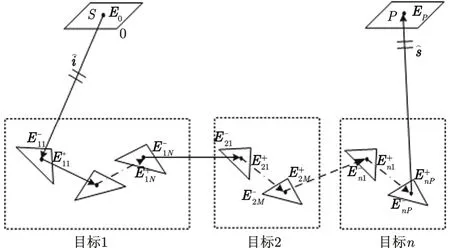
图3 射线追踪示意图Fig. 3 Sketch map of SBR

假定跟踪中心在雷达坐标系中的坐标为(xR,yR,zR)，则雷达视线在雷达坐标系下的方位角α定义为雷达视线在雷达坐标系中平面的投影与X轴的夹角，俯仰角β定义为雷达视线与Y轴的夹角，分别表示为：

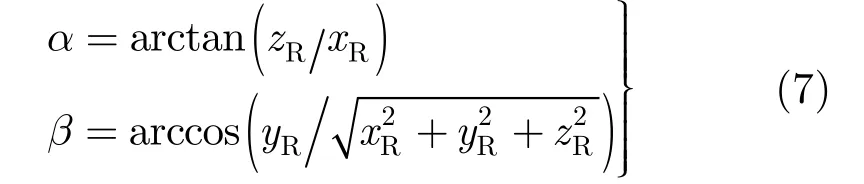
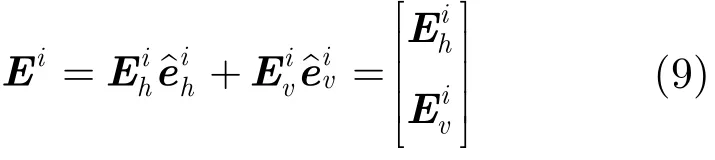
再利用PO,EEC和SBR得到目标群在给定入射方向和极化条件下的镜面反射

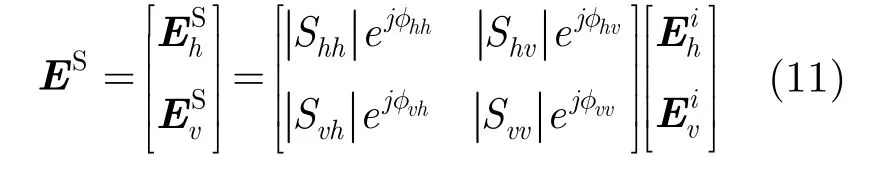
则目标动态全极化RCS可以表示为：

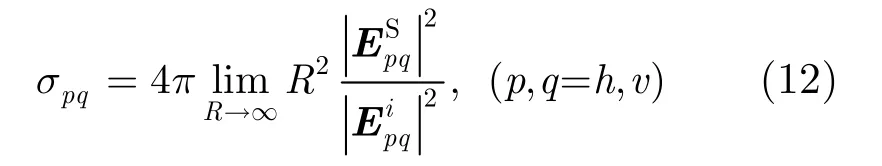
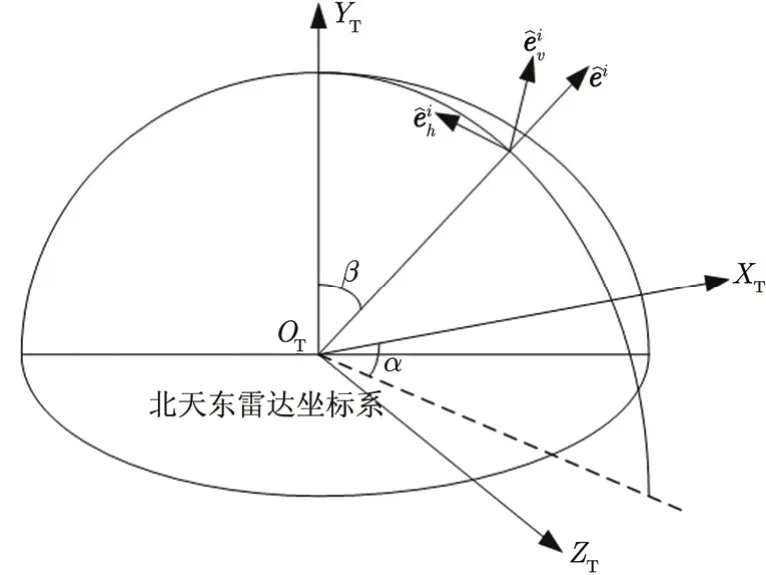
图4 雷达坐标系下的极化定义示意图Fig. 4 Sketch map of polarization under the radar coordinate system

3 算例和分析

设定某典型弹道目标群，包含弹头、助推、轻诱饵和重诱饵4个目标。弹头为一典型带尾翼弹头，结构如图5所示，目标群4个目标的结构参数如表1所示。

弹头与助推分离时间是第90 s，弹头分别于111 s和126 s时释放轻诱饵和重诱饵，弹道仿真得到各目标飞行高度随时间的变化如图6(a)所示，图6(b)是第90～161 s助推、重诱饵和轻诱饵与弹头质心间的距离。

3.1 仿真方法验证

图7是80～90 s时针对弹头目标的本文仿真结果与采用极化基变换插值得到的RCS幅度和相位对比曲线，极化基变换插值的数据为采用矩量法(MoM)获得的以0.1°间隔采样的弹头目标全极化RCS数据。其中，本文方法与极化基变换插值法之间的HH,VV,HV极化RCS幅度均方根差值分别为0.21 dB,0.12 dB,0.52 dB，相位均方根差值分别为2.3°,3.4°,8.0°，从而验证了本文方法的有效性。

图5 典型弹头结构Fig. 5 The structure of typical warhead

表1 目标群尺寸参数Tab. 1 The size parameter chart of target group

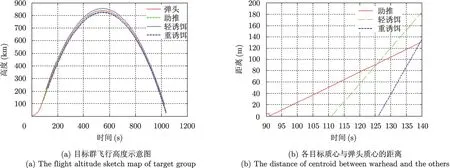
图6 目标群的飞行高度及分离时刻与弹头质心的距离Fig. 6 The flight altitude of target group and the distance of centroid in the separation time

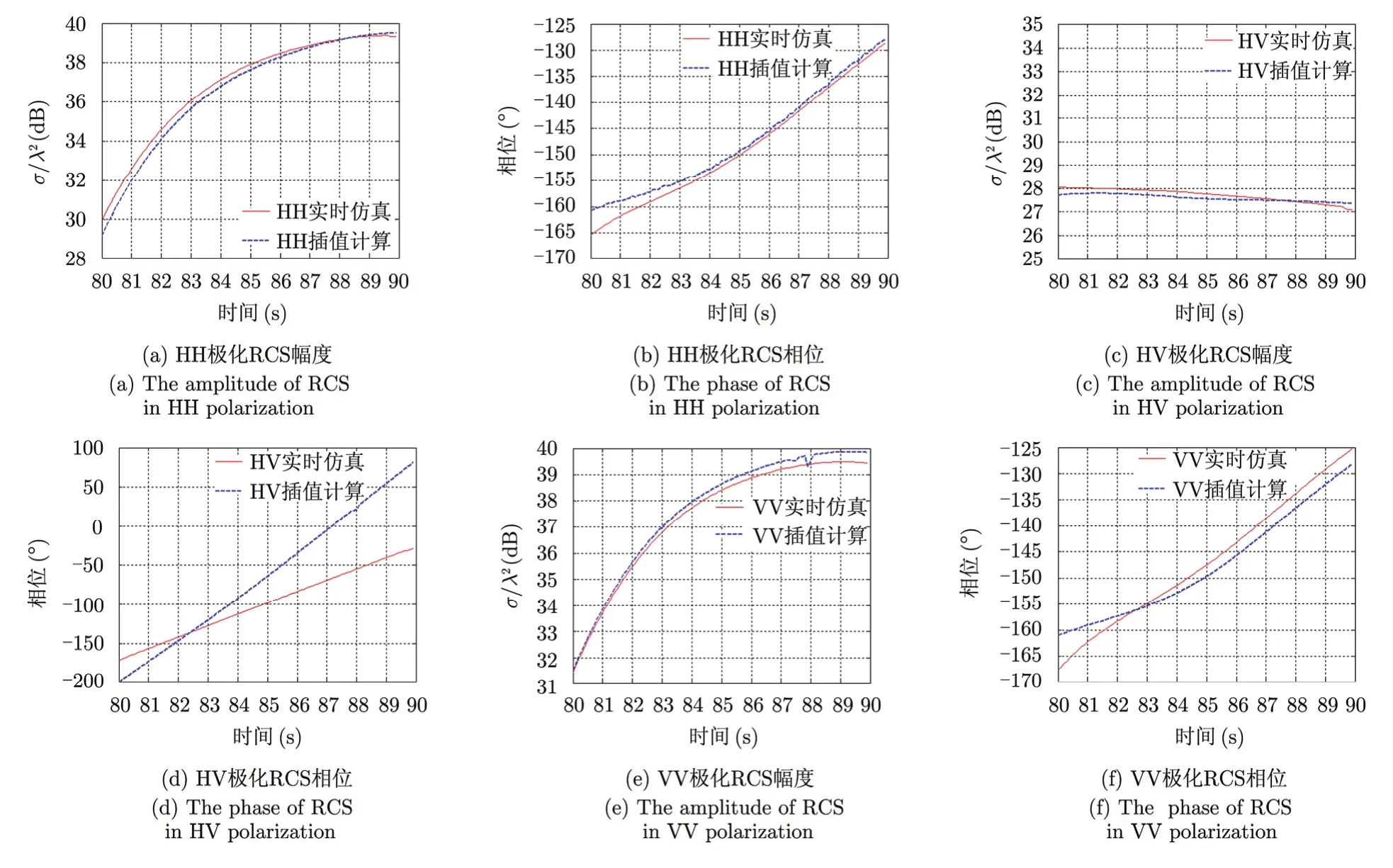
图7 弹头目标RCS仿真和插值计算比较Fig. 7 The comparison between dynamic RCS and interpolation method for missile target

在普通PC机上，本文方法计算一个采样时刻的点频RCS耗时10 s，仿真分离时段(约100个采样点)共耗时15 min；极化基变换插值法须事先利用MoM获取弹头目标全极化RCS静态数据集，即使在HP Z820高性能工作站上仍需时168 h。可见，本文方法能够在保证一定精度的条件下实现动态RCS的快速预估。

3.2 目标群场景仿真

图8是目标群在110～140 s时本文方法与极化基变换插值法得到的RCS对比曲线，极化基变换插值法的数据源是采用MoM单独计算目标群中各个目标再根据位置关系相干叠加获得的全极化RCS数据。由于目标群是动态时变的，并且未知数庞大，利用MoM无法高效获取目标群整体的RCS。

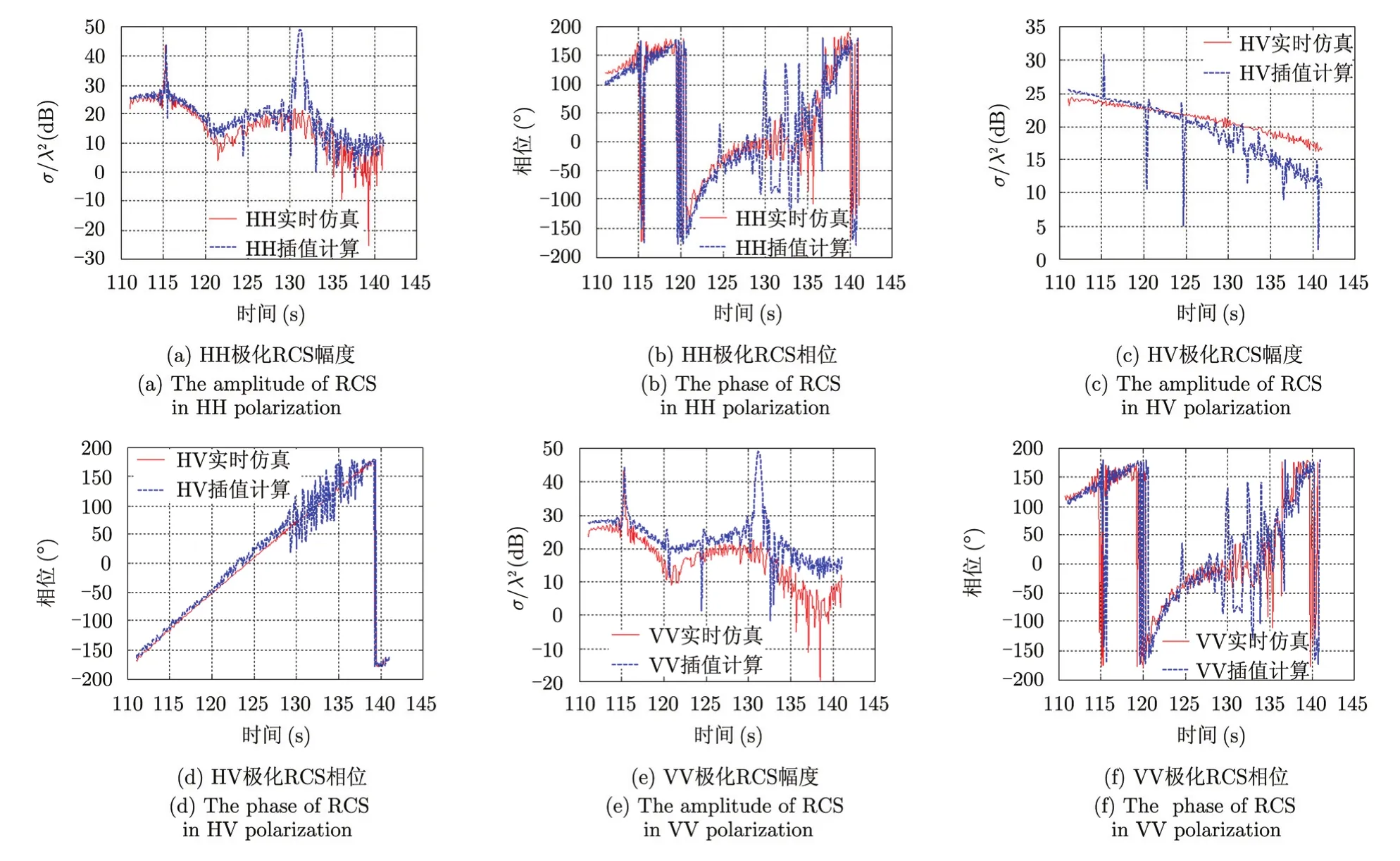
图8 目标群动态RCS仿真与插值计算比较Fig. 8 The comparison between dynamic RCS and interpolation method for target group

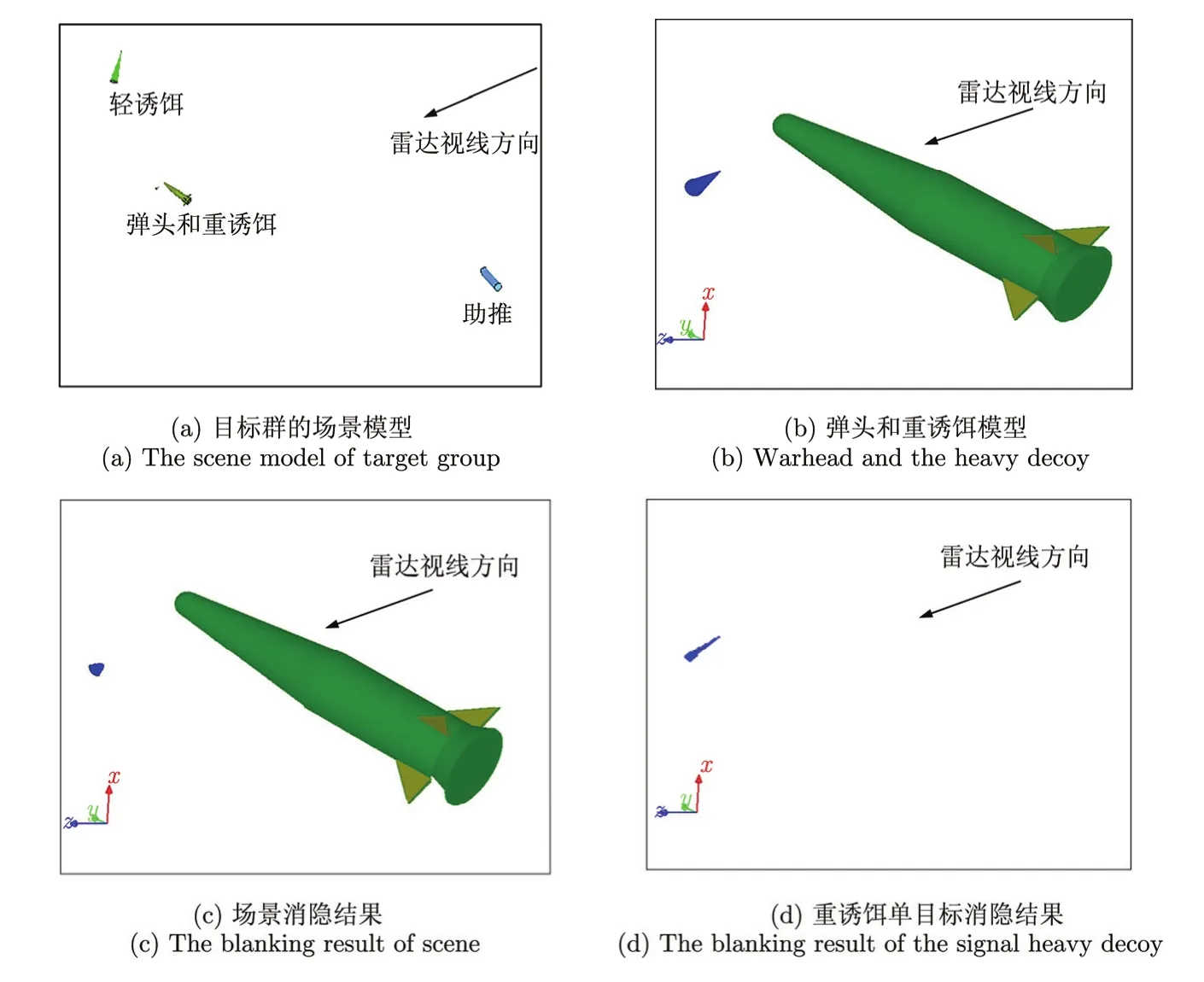
图9 分离时刻的场景模型和消隐结果Fig. 9 The scene model and the blanking results in the separation time

从图6(b)可以看出，在126～133 s之间是重诱饵与弹头分离阶段，且质心之间的距离较近，选取其中一个时刻点128 s时，雷达视线此时在雷达坐标系中的俯仰角和方位角分别为88.9°,-71.3°，图9(a)是目标群在该时刻的场景，助推级和轻诱饵离弹头较远，其相互耦合强度弱，但弹头和重诱饵离的很近。将弹头和重诱饵两目标局部放大，图9(b)是此时沿雷达视线方向弹头和重诱饵的位置关系，图9(c)是两目标沿雷达视线的消隐结果，可以判断出重诱饵被弹头遮挡。图9(d)是对此时场景中重诱饵单目标进行消隐的结果，与图9(c)的场景中的重诱饵消隐结果有明显区别，由此可见按单目标计算相干叠加的结果是不准确的。因此，在重诱饵分离的这段时间，目标群中弹头-重诱饵间存在遮挡，致使极化基变换插值方法仿真RCS误差很大，而本文方法则可获取稳定的结果。

综上所述，当目标群中各目标相互距离变大、没有遮挡和耦合时，利用单个目标静态散射数据进行极化基变换插值计算，可以得到与本文方法接近的结果，但多个目标的静态数据需要很小间隔的采样，无论是通过测量还是用数值法计算，要求的工作量巨大，通常是无法忍受的。但是，如果动态目标群在雷达视线上存在相互遮挡，或目标与目标之间存在耦合等作用时，利用单个目标进行极化基变换再插值计算的仿真方法难以实现，而本文方法依然能够得到有效的结果。

4 结论

针对弹道目标群动态RCS仿真问题，本文提出了一种基于PO+EEC+SBR的通用仿真方法实现各个飞行时刻复杂场景动态RCS快速计算。仿真试验表明，与常用的基于极化旋转基变换的插值仿真方法相比，本文方法考虑了复杂场景目标群间遮挡和多次反射影响，在保证较高计算精度的同时，具有很高的计算效率，且不存在插值误差，可为弹道目标检测和识别研究提供可靠的海量电磁散射特性数据。

[1]Chen Peng,Liu Xing,et al.. Cooperative dynamic weapon-target assignment algorithm of multiple missiles based on networks[C]. Proceedings of 2009 Control and Decision Conference (CDCC),Guilin,China,2009: 126-130.

[2]Rao S M,Wilton D R,and Glisson A W. Electromagnetic scattering by surfaces of arbitrary shape[J]. IEEE Transactions on Antennas and Propagation,1982,30(3): 409-418.

[3]Klement D,Preissner J,and Stein V. Special problems in applying the physical optics method for backscatter computations of complicated objects[J]. IEEE Transactions on Antennas and Propagation,1988,36(2): 228-237.

[4]Michaeli A. Equivalent edge currents for arbitrary aspects of observation[J]. IEEE Transactions on Antennas and Propagation,1984,32(3): 252-258.

[5]Lee S W,Ling H,and Chou R. Shooting and bouncing rays: calculating the RCS of an arbitrarily shaped cavity[J]. IEEE Transactions on Antennas and Propagation,1989,37(2): 194-205.

[6]陈行勇,陈海坚,等. 弹道导弹目标回波信号建模与雷达特征分析[J]. 现代雷达,2010,32(3): 27-31.Chen Xing-yong,Chen Hai-jian,et al.. Analysis of echo model and radar signature for a ballistic missile target[J]. Modern Radar,2010,32(3): 27-31.

[7]Zhang Xiang-kun,Zhang Yun-hua,and Chen Xiu-wei. Radar echo simulation system with flexible configuration[C]. Proceedings of 2009 2nd Asian-Pacific Conference on Synthetic Aperture Radar (APSAR),Xi’an,China,2009: 365-369.

[8]呼玮,杨建军,龙光正,等. 弹道导弹被动段动态RCS建模与仿真[J]. 电光与控制,2010,17(4): 22-25.Hu Wei,Yang Jian-jun,Long Guang-zheng,et al.. Dynamic modeling and simulation of RCS for TBM’s post-boost guidance phase[J]. Electronics Optics & Control,2010,17(4): 22-25.

[9]张居凤,冯德军,等. 雷达目标动态RCS仿真研究[J]. 系统仿真学报,2005,17(4): 834-837.Zhang Ju-feng,Feng De-jun,et al.. Simulation of dynamic RCS data of radar targets[J]. Journal of System Simulation,2005,17(4): 834-837.

[10]马梁,李永帧,等. 空间微动目标动态全极化回波仿真技术研究[J]. 系统仿真学报,2012,24(3): 628-631.Ma Liang,Li Yong-zhen,et al.. Research on simulation of dynamic full-polarization radar echo for spatial targets[J]. Journal of System Simulation,2012,24(3): 628-631.

[11]郭琨毅,盛新庆. 基于全波数值算法的扩展目标微动特征仿真[J]. 北京理工大学学报,2010,30(9): 1103-1106.Guo Kun-yi and Sheng Xin-qing. Micro-Doppler characteristics research for extended target based on full-wave numerical method[J]. Transactions of Beijing Institute of Technology,2010,30(9): 1103-1106.

[12]杨正龙,刘爱芳,等. 高速运动目标的宽带回波仿真和成像[J].现代雷达,2007,29(6): 43-48.Yang Zhen-long,Liu Ai-fang,et al.. Broadband echo simulation and imaging for fast-moving object[J]. Modern Radar,2007,29(6): 43-48.

[13]Ning Chao,Xiao Zhi-he,Wang Chao,et al.. Modeling and simulation of micro-motion in the complex warhead target[C]. Second International Conference on Space Information Technology,Wuhan,China,2007: 67955I1-7.

[14]Sun Wen-feng,Yao Han-ying,et al.. Dynamic echo simulation of precession target based on electromagnetic scattering model[C]. 2012 International Workshop on Metamaterial (Meta2012),Nanjing,China,2012: 1-4.

[15]白鹤峰,吴瑞林. 战术弹道导弹(TBM)弹道的构造方法[J].现代防御技术,1998,26(1): 39-43.Bai He-feng and Wu Rui-lin. Way of constructing TBM trajectory[J]. Modern Defense Technology,1998,26(1): 39-43.

[16]黄培康,殷红成,许小剑. 雷达目标特性[M]. 北京: 电子工业出版社,2005: 24-26. Huang Pei-kang,Yin Hong-cheng,and Xu Xiao-jian. Radar Target Characteristics[M]. Beijing: Publishing House of Electronics Industry,2005: 24-26.

[17]Gordon W B. High frequency approximations to the physical optics scattering integral[J]. IEEE Transactions on Antennas and Propagation,1994,42(3): 427-431.

[18]余定峰,何思远,等. 基于PO-EEC的各向同性介质薄层涂覆目标电磁散射[J]. 系统工程与电子技术,2012,34(12): 2427-2432.Yu Ding-feng,He Si-yuan,et al.. Electromagnetic scattering from targets coated with thin layer of isotropic dielectric based on PO-EEC method[J]. Systems Engineering and Electronics,2012,34(12): 2427-2432.

[19]汪茂光. 几何绕射理论[M]. 第2版,西安: 西安电子科技大学出版社,1994: 11-16.Wang Mao-guang. Geometrical Theory of Diffraction[M]. Second Edition,Xi’an: Xidian University Press,1994: 11-16.

Dynamic RCS Simulation of a Missile Target Group Based on the High-frequency Asymptotic Method

Zhao Tao①Dong Chun-zhu①②Ren Hong-mei②Yin Hong-cheng①②

①(Information Engineering School,Communication University of China,Beijing 100024,China)

②(National Electromagnetic Scattering Laboratory,Beijing 100854,China)

To simulate dynamic Radar Cross Section (RCS)of missile target group,an efficient RCS prediction approach is proposed based on the high-frequency asymptotic theory. The minimal energy trajectory and coordinate transformation is used to get trajectories of the missile,decoys and roll booster,and establish the dynamic scene for the separate procedure of the target group,and the dynamic RCS including specular reflection,edge diffraction and multi-reflection from the target group are obtained by Physical Optics (PO),Equivalent Edge Currents (EEC)and Shooting-and-Bouncing Ray (SBR)methods. Compared with the dynamic RCS result with the common interpolation method,the proposed method is consistent with the common method when the targets in the scene are far away from each other and each target is not sheltered by others in the incident direction. When the target group is densely distributed and the shelter effect can not be neglected,the interpolation method is extremely difficult to realize,whereas the proposed method is successful.

Radar signal processing; Missile target group; Complex scene; Electromagnetic scattering; Radar Cross Section (RCS)

TN957

2095-283X(2014)02-0150-08

10.3724/SP.J.1300.2014.13153

2013-12-31收到，2014-03-06改回；2014-03-14网络优先出版国家部委基金资助课题

*通信作者：赵涛 zhaot717@163.com