含模糊修复速率的生产库存模型

赵双双，郭嗣琮

辽宁工程技术大学理学院，辽宁阜新 123000

含模糊修复速率的生产库存模型

赵双双，郭嗣琮

辽宁工程技术大学理学院，辽宁阜新 123000

1 引言

经典的EPQ模型，通过确定最优的生产批量来实现降低总成本的目的，它通常假设生产产品完好无损。但现实生产过程中，往往由于机器故障、人员失误等原因，使得生产的过程中含有缺陷产品。而缺陷产品的存在会对最佳生产批量产生一定的影响，因此研究含有缺陷产品的生产库存问题对于企业的成功发展至关重要。

目前在含有缺陷产品的生产库存问题中，已有很多学者做出了研究。文献[1]在假设缺陷率为常数的情况下，研究了允许缺货和不允许缺货两种情况下的单周期生产库存模型；文献[2]基于检验速度的不同，建立了两种含模糊缺陷率的经济生产批量问题；文献[3]在考虑缺货的情况下，给出了含有模糊缺陷率的生产库存模型的优化求解方法，并探讨了缺陷率对生产批量的影响；文献[4]建立了库存有限且含随机缺陷率的两种EPQ模型；文献[5]研究了含有均匀分布的缺陷率且缺陷产品可全部修复为合格品的EPQ模型；文献[6]在假设缺陷率服从正态分布情况下，研究了缺陷产品可重新生产为合格产品的EPQ模型；文献[7]在假设生产过程中出现缺陷产品和废品，而缺陷产品可以全部修复的EPQ模型；文献[8]研究了库存有限且缺陷产品可修复的模糊生产库存模型；文献[9]分析了缺陷率随机且缺陷产品可修复的EPQ模型；文献[10]研究了含有一定比例的缺陷产品和一定比例的废品且缺陷产品可全部修复的EPQ模型；文献[11]在文献[2]的基础上进行了扩充，研究了缺陷产品可修复的EPQ模型；文献[12]讨论了缺陷产品可修复的模糊生产库存模型。

文献[1-4]所研究的EPQ问题虽然均考虑了缺陷产品的存在，但没有考虑对缺陷产品的重新生产问题；文献[5-12]研究了对缺陷产品进行修复的生产库存模型，但修复速率均为常数。然而，在实际生产过程中，由于生产过程中的人为失误、机器故障等因素，会产生缺陷产品，而往往缺陷产品的损坏程度是具有不确定性的，进而直接导致修复速率的不确定性，因此修复速率应为一个模糊变量；在以往诸多的模糊EPQ模型求解过程中，均涉及到了形如A～+B～X=0方程的求解，但在通常的模糊数运算过程中，此类方程是没有意义的，因为等式左端为一些模糊数的四则运算，其结果应仍为模糊数，而等式右端是一个精确数。因此，它不是普通意义下的模糊线性方程，而是在限定运算[13]意义下的一种新的模糊方程，即一种模糊限定线性方程。

综上所述，考虑到修复速度的不确定性，本文对已有的含有缺陷产品的EPQ模型进行了修改，建立了含有模糊修复速率且允许缺货的EPQ模型，为实现总成本的最小化，在求解过程中，运用模糊结构元[14]对模糊限定线性方程进行求解，进而确定模型的最优生产批量。

2 预备知识

2.1 限定运算

设Aλ为模糊数A～的λ截集，对于二元算子*，相应的限定算子*R被定义为：

2.2 模糊结构元

定义2.2.1对模糊集E而言，若它的隶属函数E(x)有下列性质：

（1）E(0)=1；

（2）在[-1,0)上E(x)单增右连续函数，在(0,1]上是单降左连续函数；

（3）当-∞＜x＜-1或者1＜x＜+∞时，E(x)=0。则将E称作模糊结构元。

若模糊结构元E满足：①∀x∈(-1,1)，E(x)＞0；②在[-1,0)上E(x)是连续且严格单调增的，在(0,1]上是连续且严格单调降的，则称E为正则模糊结构元。若E(-x)=E(x)，则称E为对称的。

定理2.2.1对于给定的正则模糊结构元E和任意有界闭模糊数A～，总存在一个在[-1,1]上单调有界的函数f，使得=f(E)。

2.3 模糊限定线性方程及结构元表示

3 含模糊修复速率的EPQ模型的建立

3.1 模型假设与符号说明

模型假设：（1）允许缺货，缺货量在下一生产周期补充；（2）产品检验周期内不会发生缺货；（3）整个生产周期的所有产品都需要检验，检验合格品在满足需求的同时，对上期缺货进行最大可能地补充；（4）仅考虑单一产品，需求连续；（5）缺陷产品经修复后，将废品一次性低价处理。

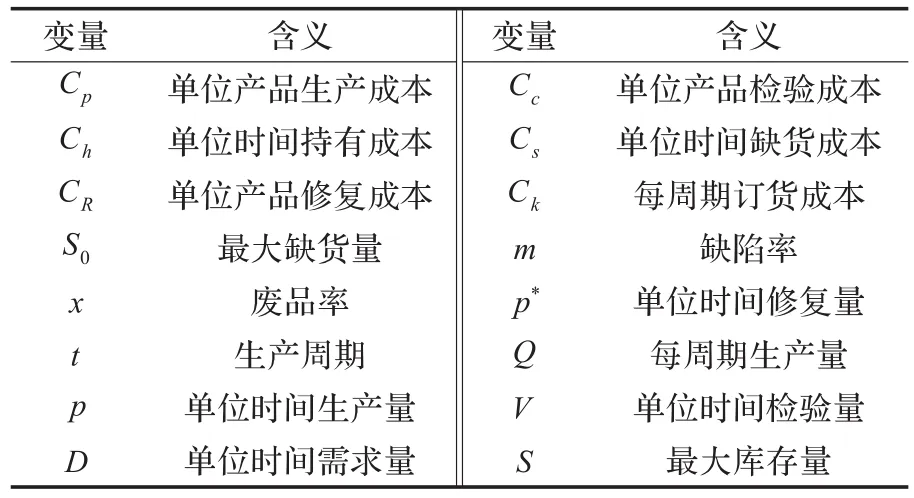
表1 各变量及其含义

3.2 模型建立

在实际生产过程中，鉴于生产速率与检验速率存在两种大小关系，本文将按生产速率与检验速率的两种大小关系对模型进行分类讨论。

模型1当检验速率小于生产速率时，即V＜p，库存量状态图如图1所示。在[0,t1]时间内，为缺货期，缺货量以速率D增加，在t1时刻形成最大缺货量S0，并以速率p开始生产，且对所生产的产品以速率V进行检验，检验合格的产品不仅要满足需求，而且要最大限度地补充缺货；[t1,t2]时间内，库存量以速率p-V(1-m)增加，缺货量以速率V(1-m)-D减少，在t2时刻缺货量补充完毕；[t2,t3]时间内，库存量以速率p-D增加，且在t3时刻，停止生产，达到最大库存量S；[t3,t4]时间内，库存量以需求速率D减少，在t4时刻，全部产品检验完毕，此时立即将缺陷品mQ以速率p*进行修复，并以速率V对修复后的产品进行检验；[t4,t5]时间内，库存量以速率p*-D增加，在t5时刻，缺陷产品修复完毕；[t5,t6]时间内，库存以需求速率D减少，在t6时刻，修复产品检验完毕，立即将废品mxQ以低价一次性处理；[t6,t]时间内，库存量继续以速率D减少，在t时刻库存量降为0，直到再次形成最大缺货量S0，开始下一周期的生产。

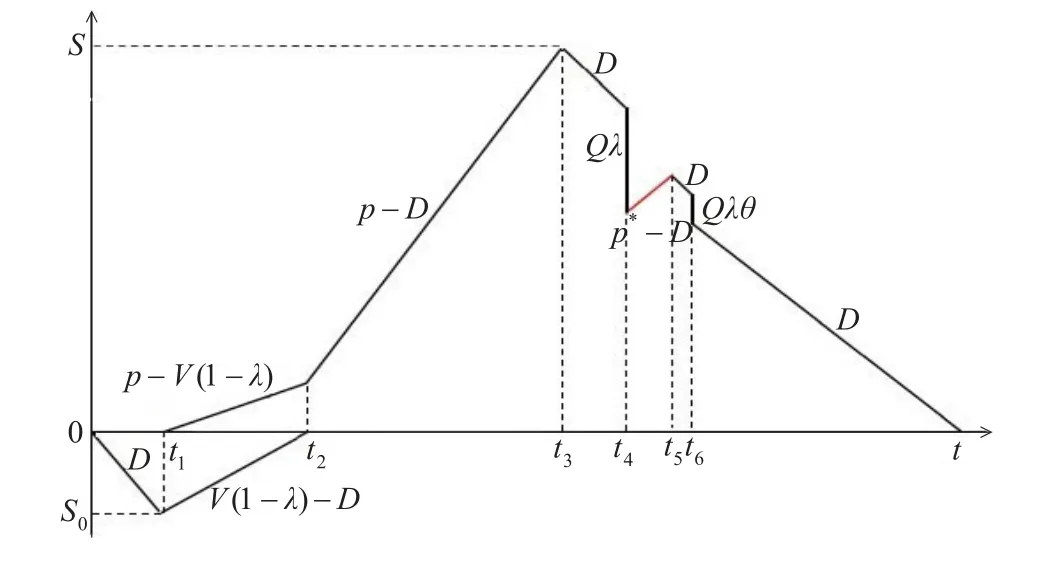
图1 V＜p时库存量状态

由以上模型分析有：

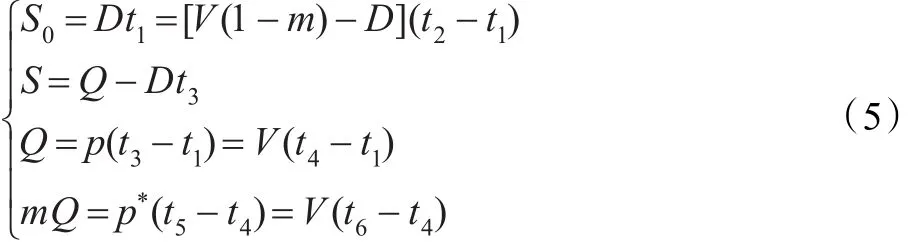
周期t内的总成本由生产成本、订货成本、修复成本、检验成本、缺货成本及库存持有成本组成，故单位时间的总成本函数：

当修复速率p*为模糊变量时，单位时间的模糊总成本函数：

模型2当检验速率不小于生产速率时，即V≥p。由于V≥p，所以，产品与缺陷品的生产停止时刻等于其检验完毕时刻，即t3=t4,t5=t6。

4 基于结构元理论的模糊EPQ模型求解

4.1 模型求解

采用模糊结构元方法进行求解，并应用Hessian矩阵的正定性来确定最小总成本的存在性。

具体求解步骤如下：

步骤1求单位时间模糊总成本函数的偏导数

由式（8），得：

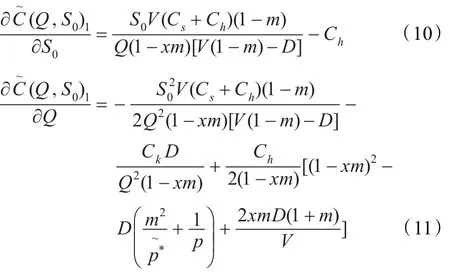
步骤2给出各模糊参数的结构元表示

由定理2.2.1可知，给定任意的正则模糊结构元E，则存在[-1,1]上的单调函数f(x)有

步骤3应用极值原理求最优生产批量

利用极值原理，令式（10）、（11）等于零，求得：

步骤4验证最小模糊生产成本的存在性

单位时间模糊总成本的Hessian矩阵可表示为：

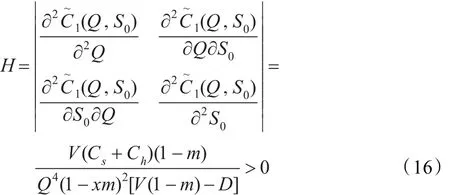
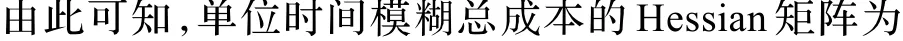
4.2 结果分析

5 实例

某生产加工厂单位产品生产成本20元，单位产品修复成本4元，单位产品检验成本1元，单位产品的缺货费10元，单位产品的日库存持有成本5元，每周期的订货成本100元，市场的日需求量200件，日生产量400件，缺陷率为0.1，废品率为0.3，缺陷产品的日修复量（480，500，520）件。试求产品的日检验量V=300时，求该加工厂的最优生产批量。

算例分析：

由图2所示，随着修复速率的模糊度的减小，最优生产批量的模糊度也减小。这是由于当订货到达时，如果修复速率的模糊度越大，那么相应的不合格品被修复的越慢，即合格品越少，则在该订货周期内不能被满足的需求数量越大，即该周期内的缺货量越大，而该周期内的缺货量将会在下一周期内进行填补，所以会导致下一周期的生产批量增大。

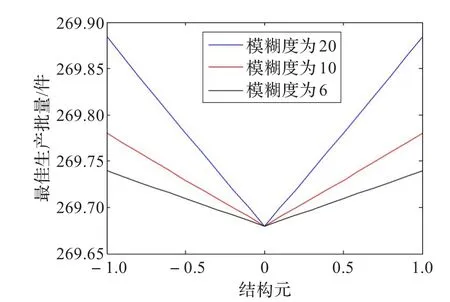
图2 修复速率对最佳生产批量的影响

由图3所示，单位时间总成本的模糊度随着修复速率的模糊度的减小而减小。这是由于修复速率的模糊度越大，那么相应的不合格品被修复的越慢，即不合格产品越多，则在该订货周期内的不合格产品大量被持有，使得持有成本增加，进而导致该周期的生产总成本增加。

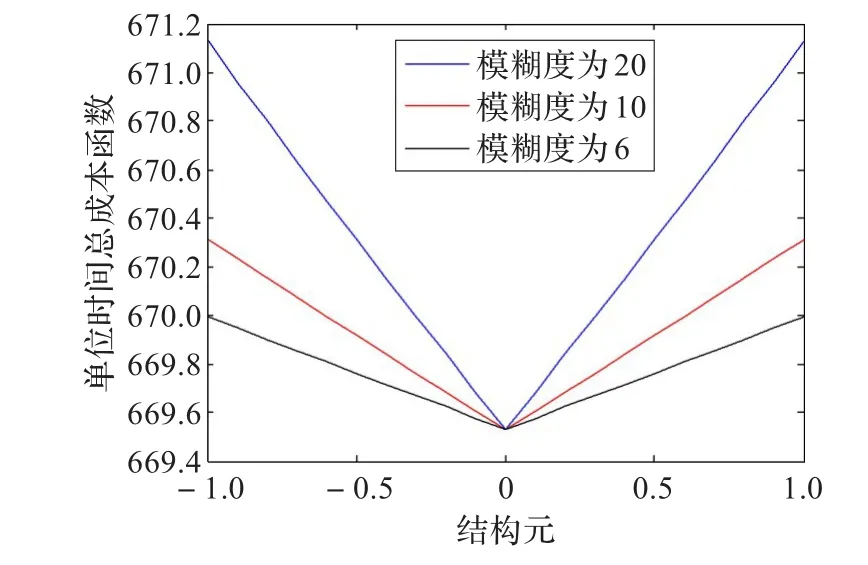
图3 修复速率对单位时间总成本的影响

6 结论

（1）在以往的缺陷品可进行修复的模糊EPQ模型基础上，鉴于缺陷产品的损坏程度的不确定性，对模型中的修复速度进行了模糊化。

（2）探讨了基于两种检验速度的含模糊修复速率的模糊生产库存问题，并给出了基于模糊结构元理论进行模糊生产总成本最小化的求解方法，同时，通过模糊生产总成本的Hessian矩阵的正定性验证了模糊生产成本最小值的存在性。

（3）通过具体的实例，证明了本文提出的EPQ问题模型的结构元解法具有较强的现实意义，且方法行之有效。结果表明，在一定的修复速率内，最佳生产批量的模糊度随着修复速率的模糊度的减小而减小。因此，在实际生产过程中，需要认真对企业生产库存条件进行分析，合理地确定修复速率的模糊度，以便获得尽可能准确的预测值。

（4）在今后的工作中，将进一步针对缺陷率及修复速率均为模糊数的生产库存模型进行研究。

[1]Jamal A M M，Sarker B R，Mondal S.Optimal manufacturing batch size with rework process at a single-stage productionsystem[J].Computers&IndustrialEngineering，2004，47（1）：77-89.

[2]郭彩云，胡劲松，王磊.模糊环境下含缺陷率且允许缺货的EPQ模型[J].计算机集成制造系统，2008，14（11）：2161-2166.

[3]李群霞，张群.考虑缺货和品的模糊生产库存模型的优化求解[J].系统工程理论与实践，2011，31（3）：480-487.

[4]韩良智.仓库容量有限时考虑产品缺陷的EPQ模型[J].系统工程与电子技术，2004，26（7）：911-913.

[5]Hayek P A，Salameh M K.Production lot sizing with the reworking of imperfect quality[J].International Journal of Production Economics，2000，67.

[6]Hayek P A，Salameh M K.Production lot sizing with the reworking of imperfect quality items producted[J]. Production Planning and Control，2001，12（6）：584-590.

[7]Chiu Y P.Determining the optimal lot size for the finite production model with random defective rate，the rework process，and backlogging[J].Engineering Optimization，2003，35（4）：427-437.

[8]贺丽，曾玲.库存有限且缺陷产品可修复的模糊生产库存模型[J].桂林电子科技大学学报，2011，31（2）：147-150.

[9]Chiu S W，Gong D C，Wee H M.Effects of random defectiverateandimperfectreworkprocessoneconomic production quantity model[J].Indust Appl Math，2004，21（3）：375-389.

[10]Chiu S W，Chiu Y P.Mathematical modelling for production system with backlogging and failure in repair[J]. Journal of Scientific and Industrial Research，2006，65（6）：499-506.

[11]胡劲松，郭彩云.含缺货且缺陷产品可修复的模糊生产库存模型[J].计算机集成制造系统，2009，15（59）：932-938.

[12]Arindam R，Kallpada M.A production inventory model with remanufacture for defective and usable in fuzzy environment[J].Computers&Industrial Engineering，2009，25（1）：87-96.

[13]Klir G J.Fuzzy arithmetic with requisite constraints[J]. Fuzzy Sets and Systems，1997，91：165-175.

[14]郭嗣琮.基于结构元理论的模糊数学分析原理[M].沈阳：东北大学出版社，2004.

[15]王世辉，郭嗣琮.一类模糊限定线性方程及其结构元求解方法[J].计算机工程与应用，2012，48（3）：37-39.

ZHAO Shuangshuang,GUO Sicong

College of Science,Liaoning Technical University,Fuxin,Liaoning 123000,China

This paper studies the problem of the Economic Production Quantity（EPQ）with repairable imperfect items and fuzzy repairable rate;The optimal production policies are determined using fuzzy structured element theory to solve the fuzzy models;The optimal production quantity with fuzzy structured element is obtained;The positive definite characteristic of Hessian matrix shows that the objective function has the minamal production inventory cost at the optimal production quantity point;The relationship between model and classical EPQ is revealed through theoretical analysis;A numerical example is given to illustrate the feasibility of using the fuzzy mathematics to solve the inventory problem.

Economic Production Quantity（EPQ）;fuzzy structuring element;fuzzy defective rate;rework;shortage

研究了缺陷产品可修复且修复速率为模糊变量情况下的生产库存模型；给出了基于模糊结构元理论的求解模糊库存总成本最小化的方法步骤；得到了含有模糊结构元的最佳生产批量的表达式；应用Hessian矩阵的正定性验证了最小成本的存在性；分析了其与经典EPQ公式之间的联系；最后通过具体算例，证明了模型求解方法的可行性。

生产库存模型；模糊结构元；缺陷率；修复；缺货

A

O159；O227

10.3778/j.issn.1002-8331.1402-0231

ZHAO Shuangshuang,GUO Sicong.Economic Production Quantity（EPQ）with fuzzy repairable rate.Computer Engineering and Applications,2014,50（22）：233-237.

教育部高校博士学科点专项科研基金（No.20102121110002）。

赵双双（1990—），女，硕士研究生，研究领域为模糊库存；郭嗣琮（1951—），男，教授，研究领域为模糊分析学、模糊预算与决策等。E-mail：460519959@qq.com

2014-02-21

2014-06-12

1002-8331（2014）22-0233-05

CNKI网络优先出版：2014-06-24,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1402-0231.html