广义犹豫模糊信息集成及其多属性群决策

胡冠中，周志刚

天津大学管理与经济学部，天津 300072

广义犹豫模糊信息集成及其多属性群决策

胡冠中，周志刚

天津大学管理与经济学部，天津 300072

1 引言

多属性群决策[1]是管理科学与决策科学相交叉的研究方向，其基本理论和决策方法已广泛应用于经济管理、模式识别、医疗诊断、投资风险等领域，因此，对多属性群决策问题的研究有着重要的理论意义和实用价值。由于客观事物的复杂性、不确定性以及人类思维的模糊性，采用确定的信息来刻画复杂问题在很多情况下并不现实，也不符合实际，因此Zadeh首先提出了模糊集（FS）[2]的概念，自此之后，模糊集理论就广泛地应用于各个领域。之后，人们提出了模糊集的几种广义形式，包括：区间模糊集[3]、直觉模糊集[4]、区间直觉模糊集[5]以及犹豫模糊集[6]等等。

算子理论是模糊理论中的一个重要组成部分。基于算术集成方法[7-10]，徐泽水和Yager提出了几种新的直觉模糊算数集成算子和直觉模糊几何集成算子[11-13]。文献[14]提出了区间直觉模糊算数平均算子，并且将其应用于区间直觉模糊环境下的多属性决策过程中。基于犹豫模糊集和直觉模糊集间的关系，夏梅梅和徐泽水[15]提出了犹豫模糊信息集成算子。Wang和Liu[16]基于Einstein运算，提出了（区间）直觉模糊Einstein加权平均算子、（区间）直觉模糊Einstein加权几何算子、（区间）直觉模糊Einstein有序加权平均算子、（区间）直觉模糊Einstein有序加权几何算子等，同时研究了这些算子间的关系与各种性质。

上述的模糊信息集成算子都是基于阿基米德T-范数和S-范数[17]的某种特殊运算提出的。基于此，本文将阿基米德T-范数和S-范数理论运用到犹豫模糊多属性群决策问题中，提出了广义的犹豫模糊有序加权平均算子，并详细讨论了它的性质，同时研究了这类算子的几类特殊形式，最后基于提出的广义信息集成算子构建了一种新的犹豫模糊多属性群决策方法，并将其应用于区域经济协调发展研究过程中。

2 相关概念

定义2.1[6]令X={x1,x2,…,xn}为一个给定的集合。形如

的二元组称为X上的犹豫模糊集（HFS）。其中(xj)是由区间[0,1]上若干个不同的数构成的集合，表示集合X中元素xj属于集合A的若干种可能隶属度。

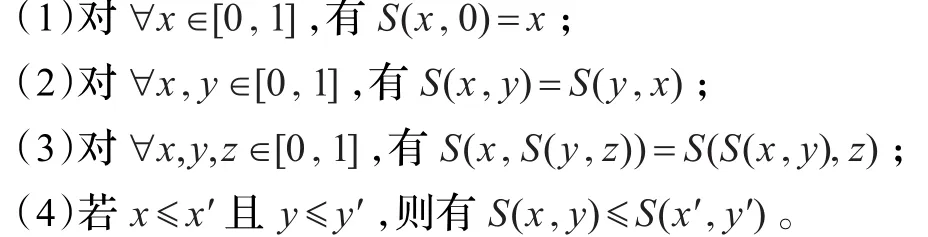
定义2.5[17]如果一个T-范数T(x,y)在定义域内连续，且满足对∀x∈(0,1)，有T(x,x)＜x，则称T(x,y)是一个阿基米德T-范数。如果一个S-范数S(x,y)在定义域内连续，且满足对∀x∈(0,1)，有S(x,x)＞x，则称S(x,y)是一个阿基米德S-范数。

由文献[17]可知，阿基米德T-范数T(x,y)可用加性算子g(x)表示为如下形式：

类似的，阿基米德S-范数S(x,y)可以表示为：

这里h(t)=g(1-t)。由于加性算子g(x)是一个严格单调递减函数，且满足g(1)=0[17]，则h(x)是一个严格单调递增函数，且h(0)=0,h(1)=1。

基于上述的阿基米德S-范和T-范数，定义如下的广义犹豫模糊运算法则。

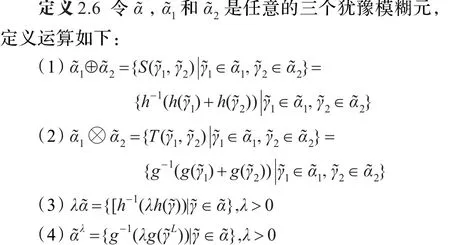
3 广义犹豫模糊有序加权平均算子及其性质

本章将基于上文中定义的犹豫模糊运算法则，提出广义犹豫模糊信息集成算子，并研究其优良性质。

为了得到广义犹豫模糊有序加权平均算子的具体表达形式，并且证明其集成结果仍是一个犹豫模糊元，则有以下定理。

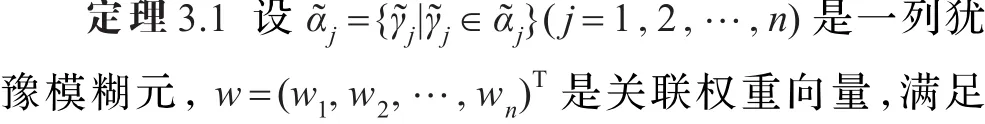
即当n=k+1时，等式（5）成立。因此，对于所有的n，等式（5）成立。

（2）接下来，将证明通过广义犹豫模糊有序加权平均算子得到的集成结果仍是一个犹豫模糊元。

即通过广义犹豫模糊有序加权平均算子得到的集成结果仍是一个犹豫模糊元。

综上，定理得证。

G-HFOWA算子具有单调性、幂等性、有界性以及置换不变性等性质。

4 广义犹豫模糊有序加权平均算子的几类特殊形式

如果对加性算子g赋予某些特定形式的函数，则可以得到一些常用的T-范数和S-范数，进而可以得到几类常见的犹豫模糊信息集成算子。

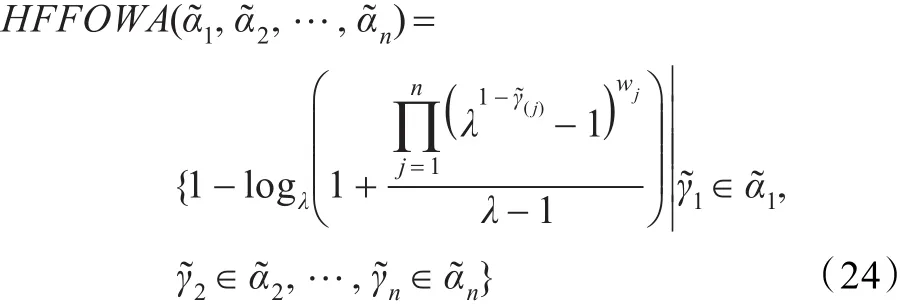
特别地，当λ→1时，HFFOWA算子就转化为HFOWA算子。

5 基于广义犹豫模糊有序加权平均算子的多属性群决策方法及其在区域经济协调发展研究中的应用

步骤5基于综合属性值(i=1,2,…,m)的序关系选择最优备选方案。越大，对应的备选方案Yi越优。

例：区域经济是在一定区域内经济发展的内部因素与外部条件相互作用而产生的生产综合体，每一个区域的经济发展都受到地方教育资源C1、社会经济条件C2、技术条件C3及人文环境C4等因素的制约。某一区域的经济发展和改革委员会欲研究本地区所属的五个辖区Yi(i=1,2,3,4,5)在上述属性指标集C={C1,C2,C3,C4}下的经济发展状况。已知属性指标集中各个因素指标的权重向量为w=(0.3,0.2,0.4,0.2)T。该区域的经济发展和改革委员会聘请若干专家对所属的五个辖区Yi(i=1,2,3,4,5)分别在上述四种属性因素下的表现进行评价，并给出了表1中的犹豫模糊决策矩阵=(j)5×4，其中(i=1,2,3,4,5;j=1,2,3,4)为犹豫模糊元。为了选出所属的五个辖区中经济能力最强劲、表现最优的辖区，将运用本文提出的多属性群决策方法，具体步骤如下：

步骤1由于所有的属性因素Cj(j=1,2,3,4)都为效益型，则决策矩阵不需要进行标准化。

步骤2基于表1中的犹豫模糊决策矩阵～=()5×4，为了简化起见，运用HFHOWA算子（即公式（23）（不失一般性，令λ=1）将五个辖区Yi(i=1,2,3,4,5)的所有属性值j(j=1,2,3,4)集结为综合属性值(i=1,2,3,4,5)，集成结果如表2所示。

表1 犹豫模糊决策矩阵D＝5×4

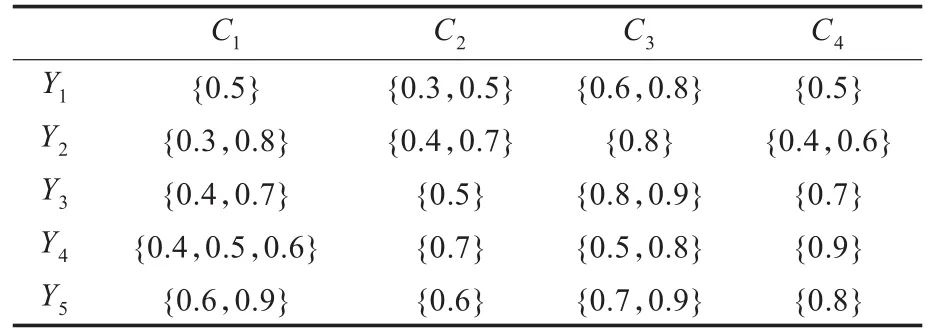
表1 犹豫模糊决策矩阵D＝5×4

C1C2C3C4 Y1 Y2 Y3 Y4 Y5 {0.5} {0.3，0.8} {0.4，0.7} {0.4，0.5，0.6} {0.6，0.9} {0.3，0.5} {0.4，0.7} {0.5} {0.7} {0.6} {0.6，0.8} {0.8} {0.8，0.9} {0.5，0.8} {0.7，0.9} {0.5} {0.4，0.6} {0.7} {0.9} {0.8}

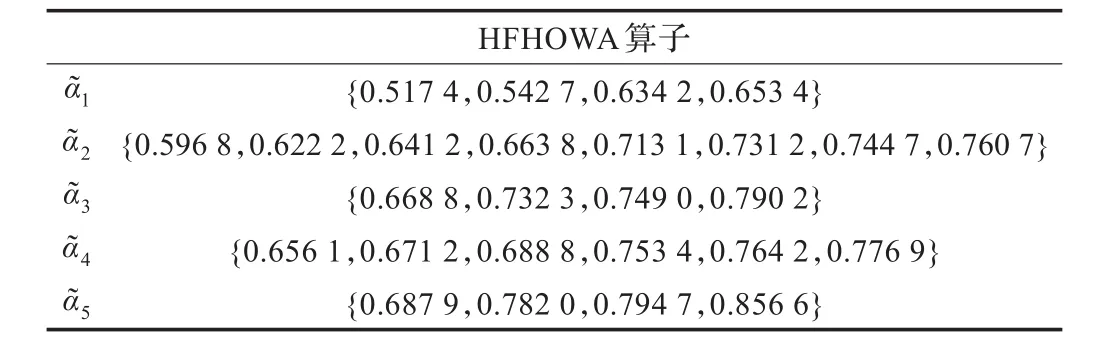
表2 利用HFHOWA算子集结得到的各辖区综合属性值

步骤3计算五个辖区综合属性值(i=1,2,3,4,5)的得分函数s()(i=1,2,3,4,5)，结果见表3。

表3 各所属辖区综合属性值的得分函数

步骤4依据定义2.2，将综合属性值(i=1,2,3,4,5)进行大小排序，如表4所示。

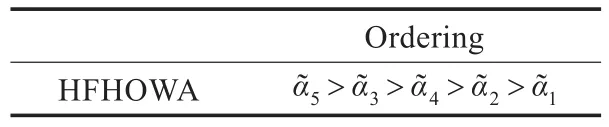
表4 各综合属性值的排序结果

步骤5根据综合属性值(i=1,2,3,4,5)的序关系对所属五个辖区Yi(i=1,2,3,4,5)进行优劣排序，见表5。从表5可知，利用HFHOWA算子集成得到的经济能力最强劲、表现最优的辖区为Y5，其结果与应用文献[15]中的决策方法所得到的结果一致。

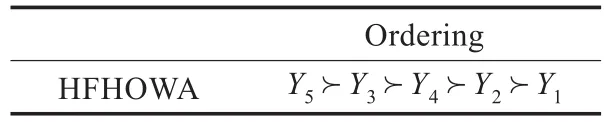
表5 备选方案的排序结果

6 结论

目前，犹豫模糊环境下的信息集成算子已出现在很多文献中，但是都没有将这些算子进行推广统一。本文基于阿基米德T-范数和S-范数，首先定义了广义犹豫模糊运算法则，接着提出了广义犹豫模糊有序加权平均算子，并研究了其性质，包括：单调性、幂等性、有界性以及置换不变性；接着探讨了广义犹豫模糊有序加权平均算子的几类常见的形式，如：犹豫模糊有序加权平均算子、犹豫模糊Einstein有序加权平均算子等等；在犹豫模糊环境下，基于广义犹豫模糊有序加权平均算子构建了一种新的多属性群决策方法，并将其运用于区域经济协调发展研究过程中。

[1]Hwang C L，Yoon K.Multiple attribute decision making and applications[M].New York：Springer-Verlag，1981.

[2]Zadeh L A.Fuzzy sets[J].Information and Control，1965，8（3）：338-356.

[3]Turksen I B.Interval valued fuzzy sets based on normal forms[J].Fuzzy Sets and Systems，1986，20：191-210.

[4]Atanassov K T.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，1986，20（1）：87-96.

[5]Atanassov K，Gargov G.Interval-valued intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，1989，31：343-349.

[6]TorraV.Hesitantfuzzysets[J].InternationalJournalof Intelligent Systems，2010，25：529-539.

[7]Zhang G Q，Lu J.An integrated group decision-making method dealing with fuzzy preferences for alternatives and individual judgments for selection criteria[J].Group Decision and Negotiation，2013，12（6）：501-515.

[8]Yager R R，Filev D.P.Induced ordered weighted averaging operators[J].IEEETransactionsonSystems，Man，and Cybernetics-Part B，1999，29：141-150.

[9]Liu X W，Chen L.On the properties of parametric geometric OWA operator[J].International Journal of Approximate Reasoning，2004，35：163-178.

[10]Liu X W.On the properties of equidifferent OWA operator[J].InternationalofApproximateReasoning，2006，43：90-107.

[11]XuZ.S.Intuitionisticfuzzyaggregationoperators[J]. IEEE Transactions on Fuzzy Systems，2007，15：1179-1187.

[12]Xu Z S，Yager R R.Some geometric aggregation operators based on intuitionistic fuzzy sets[J].International Journal of General Systems，2006，35：417-433.

[13]Yager R.R.Induced aggregation operators[J].Fuzzy Sets and Systems，2003，137：59-69.

[14]Xu Z S，Chen J.Approach to group decision making based on interval-valued intuitionistic judgment matrices[J].Systems Engineering-Theory and Practice，2007，27：126-133.

[15]Xia M M，Xu Z S.Hesitant fuzzy information aggregation in decision making[J].International Journal of Approximate Reasoning，2011，52：395-407.

[16]Wang W Z，Liu X W.Intuitionistic fuzzy information aggregationusingEinsteinoperations[J].IEEETransactions on Fuzzy Systems，2012，20：923-938.

[17]Sugeno M.Theory of Fuzzy Integral and its Application[M]. Tokyo Institute of Technology，1974.

[18]金飞飞，裴利丹，陈华友，等.犹豫模糊EWAA算子及其多属性决策方法[J/OL].计算机工程与应用，http://www.cnki. net/kcms/detail/11.2127.TP.20130521.1027.010.html.

HU Guanzhong,ZHOU Zhigang

College of Management and Economics,Tianjin University,Tianjin 300072,China

Based on the Archimedean t-norm and s-norm,the generalized hesitant fuzzy information aggregation operator is proposed under hesitant fuzzy environment,and a new method for multi-attribute group decision making is developed. The generalized hesitant fuzzy operational laws are defined,which is based on the Archimedean t-norm and s-norm.The generalized hesitant fuzzy ordered weighted averaging operator is proposed,and then discusses some of its desirable properties in detail.Discuss in some special circumstances,the generalized hesitant fuzzy ordered weighted averaging operator will be convert into some common hesitant fuzzy information aggregation operators,such as hesitant fuzzy ordered weighted averaging operator,hesitant fuzzy Einstein ordered weighted averaging operator,hesitant fuzzy Hamacher ordered weighted averaging operator and hesitant fuzzy Frank ordered weighted averaging operator.A new approach to hesitant fuzzy multi-attribute group decision making is presented based on the proposed operator,and then apply the developed approach to research on the coordinated development of regional economy,and illustrate the behavior of the proposed approach.

hesitant fuzzy set;multi-attribute group decision making;Archimedean t-norm and s-norm;aggregation operator

在犹豫模糊环境下，主要研究了基于阿基米德范数的广义信息集成算法，并提出了一种新的多属性群决策方法。基于阿基米德T-范数和S-范数，定义了广义犹豫模糊运算法则；运用新定义的广义犹豫模糊运算法则，提出了广义犹豫模糊有序加权平均（G-HFOWA）算子，研究了其优良性质；探讨了在某些特殊情况下，广义犹豫模糊有序加权平均算子将转化为一些常见的犹豫模糊信息集成算子，包括犹豫模糊有序加权平均算子、犹豫模糊Einstein有序加权平均算子、犹豫模糊Hamacher有序加权平均算子以及犹豫模糊Frank有序加权平均算子；基于广义信息集成算子，构建了一种新的犹豫模糊多属性群决策方法，并将其应用于区域经济协调发展研究过程中，以验证提出的决策方法是可行的与有效的。

犹豫模糊集；多属性群决策；阿基米德T-范数和S-范数；集成算子

A

O22

10.3778/j.issn.1002-8331.1407-0370

HU Guanzhong,ZHOU Zhigang.Generalized hesitant fuzzy information aggregation and applications to multi-attribute group decision making.Computer Engineering and Applications,2014,50（22）：38-42.

教育部科学研究重大课题攻关项目（No.11JZD038）。

胡冠中（1985—），男，博士研究生，研究方向：管理科学，区域经济；周志刚（1950—），男，博士，博士生导师，教授，研究方向：管理科学，人力资源开发与管理。E-mail：shexian19880129@163.com

2014-07-23

2014-09-09

1002-8331（2014）22-0038-05

CNKI网络优先出版：2014-10-21,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1407-0370.html

◎理论研究、研发设计◎