基于改进蚁群算法的应急救援路线选择
2014-08-03崔丽群张明杰
崔丽群,张明杰,许 堃
1.辽宁工程技术大学 软件学院,辽宁 葫芦岛 125105
2.辽宁工程技术大学 通信学院,辽宁 葫芦岛 125105
基于改进蚁群算法的应急救援路线选择
崔丽群,张明杰,许 堃
1.辽宁工程技术大学 软件学院,辽宁 葫芦岛 125105
2.辽宁工程技术大学 通信学院,辽宁 葫芦岛 125105
1 引言
随着我国经济的快速发展,城市规模迅速扩大,人民生活水平显著提高,由此带来的交通问题和社会安全问题日益突显出来。自然灾害、公共卫生事件、生产安全事故和恐怖袭击等紧急、突发事件时有发生,应急救援已成为社会生活方面不可缺少的一个部分。为实现快速高效的应急救援,路线的选择问题不容回避。应急救援路线是指在当时的交通条件下,为实现快速高效的应急救援如何选择交通线路的问题。应急救援最突出的要求是时间,因为面对突发事件和灾害,救援人员和物质如能在最短的时间到达,才能发挥其作用,最大限度地减少灾害后果[1]。
为此,国内外对应急救援路线的优化做了大量研究。国外仿生智能优化算法解决路径优化问题是一个研究热点问题,蚁群算法的研究尤其突出。蚁群算法最早称为AS(Ant System),其成功应用于解决旅行商问题[2-3]。随后又出现了精英策略蚂蚁系统(Elitist Strategy Ant System,ESAS)、基于排列的蚂蚁系统(A-ant SystemRank,ASR)、最大最小蚂蚁系统(MAX-MIN Ant System,MMAS)[4]。1996年 Gambardella和 Dorigo提出的蚁群系统(Ant Colony System,ACS)受到普遍关注[5-6]。对于用蚁群算法解决应急救援路线选择的研究,目前还没有成熟的理论成果。
国内关于路径优化问题的研究主要借鉴国外成果,理论研究已经很成熟,但实际应用不多。国内的蚁群算法研究始于1998年末,主要围绕TSP(旅行商问题)及相关问题进行研究,以及应急救援路线的选择和蚁群算法在连续系统的应用。本文针对蚁群算法的缺陷和应急救援路线选择的特点,主要研究了改进蚁群算法在应急救援路线选择中的应用,为城市应急救援路线选择提供了有效的解决方案。
2 应急救援路线选择的数学模型
应急救援线路的选择[7-9],强调的是时间,因为在越短的时间内做出救援,挽救生命和财产的概率就越大。这个问题同最短路线的选择有很大的不同,路线最短并不能代表所用时间是最少的。影响时间的因素[10]有很多,比如道路等级、路面质量、交通流量、车辆限制、气象条件、道路实时信息等等,都对救援时间产生影响,在救援行动时都要考虑在内,因此应急救援线路的选择要考虑更多的情况,比求解最短路线有更大的复杂性。
2.1 影响应急救援路线选择的因素
应急救援路线选择是基于城市交通路线的[11-12],因为相比较于乡村的路线,城市交通路线有很大的复杂性,乡村道路比较单一,救援相对简单易行。鉴于城市交通的特点,影响应急救援路线选择的因素概括为以下几个方面。
(1)实际路线距离d。路线距离的长短,显著的影响着路线行驶时间,对于现有的交通工具来说,其速度v取值波动范围不是很大,故路线行驶时间受路线长短的制约。
(2)道路状况θ。这里所讲的道路状况包含所有的路面情况,如道路等级、路面质量等。道路状况分为不通(1)、凹凸土路(0.9)、窄土路(0.8)、宽土路(0.7)、窄砖路(0.6)、宽砖路(0.5)、窄水泥路(0.4)、窄柏油路(0.3)、宽水泥路(0.2)、宽柏油路(0.1)。
(3)交通状况ω。这里的交通状况也是包含了所有的交通信息,比如道路上交通车辆的多少、道路管制情况、交通实时信息等。交通状况可分为阻塞不通(1)、严重阻塞(0.9)、车辆拥挤(0.8)、交通混乱(0.7)、人车混合(0.6)、过饱和(0.5)、车辆饱和(0.4)、车辆适中(0.3)、稍有车辆(0.2)、车辆稀少(0.1)、道路空闲(0)。
(4)实时天气情况w。实时天气信息对于应急救援路线的选择也是一个比较重要的因素,实时天气状况分为暴雨或雪(0.8)、中雨或雪(0.6)、小雨或雪(0.4)、阴(0.2)、晴(0)。
2.2 应急救援交通网的数学描述
交通路线从地图上看,是点和线的交织。对应到数学上为一无向图G(V,E),其中V是点的集合,E是线的集合,也就是点和线构成了无线图。根据这一相似性,将交通路线网中的道路交点看成无向图中的点,道路交点间的路线看成无向图中的线,这样交通网抽象到数学上就是一个无向图。
城市应急救援是从一个地点到另一个地点的救援,但从一个地点到路口的那段距离是必须要走的,不管那段路线状况如何,救援车辆必须经过,因此,在寻求最优路线时,这段路程可以不予考虑,直接是路口到路口间的路线选择,在数学实现上,也就是求无向图中点到点的最优路线。
按照上述原理,救援路线的选择也就是求无向图中节点到节点的最优线路。因此可以将实际交通路线选择的问题转化为数学上的求解问题。基于蚁群算法在求解优化问题上的优越性,数学模型的求解应用蚁群系统[13]来实现。
2.3 应急救援线路选择数学模型的建立
应急救援路线选择的数学模型的目标函数是求城市中两点之间用时最少的行驶路线,即TAB=min∑tij,其中i,j为所选路线上的点,A,B分别为出发点和终点。
在求出发点到达终点之间用时最少的路线时,考虑到影响应急救援选择的因素,在进行算法循环迭代过程中,分别引入 wij、θij、ωij等“状态参数”表示实时天气情况、道路状况、交通状况等不确定因素对救援线路选择的影响。考虑到这些影响后,本文使用当量长度Dij来代替实际路径长度dij:

其中 wij、θij、ωij这些影响因素系数的计算如下:设某一影响因素的影响程度的系数为β,且有该影响因素时通过i、j之间的路径的时间为Tij,无此影响因素时通过i、j之间路径的时间为tij,则通过此路径时的影响因素系数 β为:

假设当前路段车辆所占车道的交通流量为φ,i、j之间路段当前理想流量为ϕij,当前车辆行驶速度为v,则可计算出当前i、j之间路段(dij)上的平均行车速度vij为:

那么救援路线行驶时间t为:

3 改进蚁群算法对应急救援路线选择的过程
比较于基本蚁群算法[14]的求解步骤,改进蚁群算法求解具体的求解步骤如下:
(1)选取k个较差救援路线。根据路线已知的属性信息,利用TOP-K排序算法输出k个较差路线。算法模型中涉及的路线属性有4个,分别为路线距离d、道路状况θ、交通状况ω以及实时天气情况w,相关的打分函数为:

(2)算法参数的初始化。算法参数的初始化按经验实验值选取,在算法模型里k个较差边的信息素初值给予很小的数值,以区别于其他的路线。
(3)人工蚂蚁的初始分布。利用应急救援路线数学模型,是求解两点间的时间最优路线,故蚂蚁的初始分布是所有的蚂蚁都位于出发点或终止点。

(5)进行信息素更新,并清空禁忌表。信息素更新分为两部分,全局更新和局部更新,分布按下式进行,信息素更新完毕,一轮搜索结束,将禁忌表清空,为下一轮搜索做好准备。

信息素挥发因子ρ的大小直接影响着蚁群算法的全局搜索能力及其收敛速度,ρ过大会降低全局搜索能力,ρ过小会降低算法的收敛速率。信息素挥发因子ρ按下式进行更新。

(6)计算最优路线,判断是否满足结束条件。如满足结束条件,输出最优路线;否则,转入第(3)步,开始新一轮的搜索。
4 仿真实验及结果分析
用Matlab7.0在Windows XP平台上对本文改进算法的效果进行验证,为进一步验证算法的有效性,同时与文献[15]中提供的K-均值算法的结果进行了比较,文献中的参数与本文改进的算法的参数一样。在算法模型里k个较差边的信息素初值给予较小的数值,具体参数设置:m=50,τ=α=β=1,ρ=0.4,γ=3,最大搜索次数为100,距离取实际值。实验选取具有20个节点(道路交叉点)的城市交通图进行分析,图1表示该城市的交通简化图。
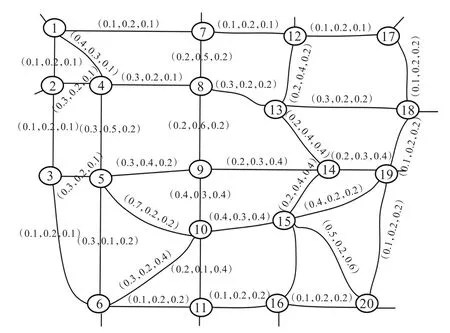
图1 城市交通简化图
依据算法理论编写应用程序,分别用K-均值蚁群算法和改进后的算法求解节点1到节点14的应急救援路线,并对实验结果进行对比。
(1)K-均值蚁群算法和改进后算法的运行结果
K-均值蚁群算法运行20次所得最优结果如图2所示,路线为1→2→4→8→13→14,所用时间为0.415 5 h,路线长度为23.120 6 km。
改进算法运行20次所得最优结果如图3所示,路线为1→7→8→13→14,用时为0.414 8 h,路线长度为23.120 5 km。
(2)实验结果及总结
通过图2和3比较,改进的算法得到了最优结果,K-均值蚁群算法没有得到最优结果。算法改进前后各自运行10次所得结果对比见表1,表中数据显示,改进算法的寻优能力增强,能找到全局最优路线,而K-均值蚁群算法收敛到了局部最优,没有找到最优结果。

图2 K-均值算法运行结果

图3 改进算法运行结果
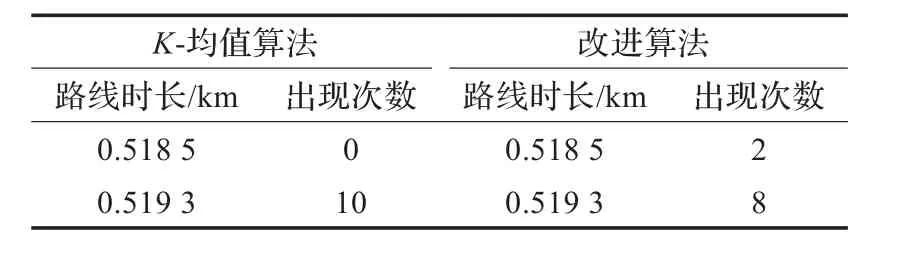
表1 算法结果对比
对K-均值算法和改进算法分别运行3次的平均时间和最短时间的对比如图4和5所示。K-均值算法运行3次,如图4所示,只有1次稳定到了最优解,稳定到最优解时的迭代次数为58,其余2次都未能最终收敛到最优路线,其波动性大,具有不稳定性;改进后的算法3次全部稳定到了最优解,如图5所示,系统稳定性强,稳定到最优解时的最少迭代次数为15,比K-均值算法提前43次。

图4 K-均值算法平均时间和最短时间3次结果

图5 改进算法平均时间和最短时间3次结果
实验结果对比研究分析,在改进后的蚁群算法求解应急救援路线在仿真实验中,证明了改进后的算法不论在收敛速度、全局最优,还是稳定性方面都得到了显著的改善,为解决实际问题提供了可行的方法和思路。但改进的算法还存在有不足之处,比如寻找全局最优解的能力还不稳定等,针对大规模问题的研究还没有实验验证等。还有待进一步的研究和学习。
5 结束语
本文在基本蚁群算法的基础之上,分析了其特点,在提高蚁群算法的收敛速率和算法稳定性方面给出了改进方案,并结合现有的研究成果将改进后的蚁群算法应用到应急救援路线选择问题上。提出了应急救援路线选择的蚁群算法的数学模型,并给出了改进蚁群算法求解模型的方法和步骤。实验验证了该数学模型可以很好地应用到求解应急救援路线选择问题上,能为应急救援指挥提供决策依据。本文所研究的改进蚁群算法求解应急救援路线选择的问题取得了初步成果,但应急救援路线的选择是一个很复杂的问题,下一步要研究的问题主要有:实时性的应急救援路线选择的问题以及大规模的应急救援路线选择及多个应急救援的组合问题等。
[1]刘勇,马欣,审志兵.基于改进蚁群算法的应急救援最优路径选择[J].工业安全与环保,2009,35(11):56-57.
[2]Dortgo M,Maniezzo V,Colorni A.Ant system:optimization by a colony cooperating agents[J].IEEE Trans on Systems,Man,and Cybernetics Part B:Cybernetics,1996,26(1):29-41.
[3]Dortgo M,Gambardella L M.Ant colony system:a cooperative learning approach to the traveling salesman problem[J].IEEE Trans on Evolutionary Computation,1997,1(1):53-56.
[4]Stutzle T,Belgium B.Max-min ant system[J].Elsevier Sci,1999,17.
[5]Dorigo M,Gambardella L M.Ant colony system:a cooperative learning approach to the traveling salesman prob-lem[J].IEEE Trans on Evolutionary Comp,1997,1(1):53-66.
[6]Le Louarn F X,Gendreau M,Potvin J Y.GENI ants for the traveling salesman problem[J].Annals of Operations Research,2004,131(10):187-201.
[7]Li Ziyao.Fuzzy clustering analysis of emergency rescue route[C]//2011 2nd International Conference on Artificial Intelligence and Electronic Commerce,2011:1148-1151.
[8]Li Baojie,Gu Hehe,Ji Yazhou.Selection of optimal emergency rescue route based on improved ant colony algorithm[C]//2010 18th International Conference on Geoinformatics,2010:1-4.
[9]Zhang Jie,Wang Zhiyong,Xu Weisheng,et al.Model and solution of rescue path selection in emergency[J].Application Research of Computers,2011,28(4):1311-1314.
[10]刘勇.基于蚁群算法的应急救援最优路径研究[D].北京:中国地质大学,2010.
[11]Wang Qiuping,Du Yefan,Wu Jinpu.Study on traffic impedance based on grey theory[C]//The 9th International Conference of Chinese Transportation Professional,2009.
[12]Wang Qiuping,Du Yefan,Wu Jinpu.Study on the vertical optimization arrangement of nodes in comprehensive industrial pipelines[C]//International Pipelines and Trenchless Technology Conference,2009.
[13]Mullen R J,Monekosso D,Barman S,et al.A review of ant algorithms[J].Expert Systems with Application,2009,36(6):9608-9617.
[14]吴斌,赵燕伟.蚁群算法的研究现状[J].自动化仪表,2004,25(1):1-3.
[15]乔梁,金华,李云霄,等.K-均值算法混合蚁群算法城市应急救援最佳路径决策[J].中国公共安全:学术版,2011,23(2):53-57.
CUI Liqun,ZHANG Mingjie,XU Kun
1.College of Software,Liaoning Technical University,Huludao,Liaoning 125105,China
2.College of Communication,Liaoning Technical University,Huludao,Liaoning 125105,China
The choice of emergency rescue route is related to the success or failure of emergency rescue,and it has great significance for saving lives and properties to select a reasonable and effective emergency rescue route,and it belongs to the field of combinatorial optimization.For the slow solution,poor algorithm stability,prone to premature or stagnation and other defects of ant colony algorithm and characteristics of emergency rescue route choice,this paper mainly studies the application of improved ant colony algorithm in emergency rescue route choice and provides an effective solution for city emergency rescue route choice and according to the practical application proposes mathematical model of ant colony algorithm of emergency rescue route choice.It is proved by experiments that the model which applied to solving problems of emergency rescue route choice has fast and efficient features.
emergency rescue;ant colony algorithm;Top-K sorting algorithm
应急救援路线的选择关系到应急救援的成败,合理有效地选择应急救援路线对挽救生命和财产具有重要意义,其属于组合优化问题。针对蚁群算法求解速度慢、算法稳定性差、易出现早熟或停滞等缺陷和应急救援路线选择的特点,主要研究了改进蚁群算法在应急救援路线选择中的应用并根据实际应用提出了应急救援路线选择的蚁群算法的数学模型,为城市应急救援路线选择提供了有效的解决方案。通过实验证明该模型可以应用到解决应急救援路线选择问题方面,具有快速、高效的特点。
应急救援;蚁群算法;TOP-K排序算法
A
TP301
10.3778/j.issn.1002-8331.1301-0098
CUI Liqun,ZHANG Mingjie,XU Kun.Improved ant colony algorithm for emergency rescue route choice.Computer Engineering and Applications,2014,50(23):256-260.
辽宁省教育厅高等学校科研项目(No.2009A349);辽宁省教育厅基金项目(No.2009A350)。
崔丽群(1969—),女,副教授,硕士研究生导师,主要研究方向为嵌入式系统和软件工程;张明杰(1987—),男,主要研究方向为嵌入式系统。E-mail:zhangmj_keda@163.com
2013-01-10
2013-04-22
1002-8331(2014)23-0256-05
CNKI网络优先出版:2013-05-13,http://www.cnki.net/kcms/detail/11.2127.TP.20130513.1601.005.html
