虚拟结点法在多出口疏散方案中的适用性分析
2014-08-03谢君,万庆,张弛,李强,李响
谢 君,万 庆,张 弛,李 强,李 响
1.华东师范大学 地理信息科学教育部重点实验室,上海 200241
2.中国科学院 地理科学与资源研究所,北京 100101
3.中国科学院 新疆生态与地理研究所,乌鲁木齐 830011
4.中国人民解放军95806部队
5.清华大学 建筑学院,北京 100084
虚拟结点法在多出口疏散方案中的适用性分析
谢 君1,万 庆2,张 弛3,李 强4,5,李 响1
1.华东师范大学 地理信息科学教育部重点实验室,上海 200241
2.中国科学院 地理科学与资源研究所,北京 100101
3.中国科学院 新疆生态与地理研究所,乌鲁木齐 830011
4.中国人民解放军95806部队
5.清华大学 建筑学院,北京 100084
1 引言
城市的规模及人口密度随着城市化进程的推进而不断扩大,在此背景下,制定合理的撤离方案快速地组织人员在存在危险时有序地撤离到安全地区已经成为一个重要的问题。
目前,已有一些学者对突发事件应急疏散问题进行了多方面的研究。一些研究从宏观模型的角度考虑[1],对疏散地区或建筑建立模型,应用网络流解决疏散问题,以达到系统最优的目的。如Bretschneider及Kimms用混合整数规划模型设计避免冲突的疏散路线,并采用启发式方法解决高频的计算量[2]。Yamada将城市模拟为无向图,采用网络流中的最短路径方法制定疏散人群到避难场所的路径,最小费用流方法解决避难场所的容量限制问题[3]。Liu等利用元胞传输模型将网络按照突发事件的影响程度分成几个区域,越靠近事发地点遭受的影响越严重,需要越快撤离。因此,采用分阶段疏散策略确定各个区域疏散时间。在分阶段疏散建模中,只有每个区域的开始撤离时间是可控制的。此分阶段疏散策略通过在允许的安全时间窗内达到更统一的需求分布,从而大大减少疏散网络的拥堵[4]。Li等提出了一种基于网络的分阶段疏散算法(下文简称分阶段算法),该方法将地理位置相近的人员划分为一个疏散小组,通过为每个疏散小组安排疏散出发时间并设计疏散路线,避免在疏散过程中不同疏散组之间可能产生的冲突,提高总体疏散效率。该方法为单个安全出口的应急疏散提供了一个较为有效的解决办法,但尚不支持多出口情形,因此有一定的局限性[5]。Saadatseresht等采用多目标进化算法进行疏散规划,在选择每个建筑群的安全撤离区后,利用多目标优化问题求解疏散规划问题,同时考虑距离与安全区容量两个因素,应用MATLAB中的NSGA-II完成疏散规划[6]。
较之宏观模型强调均一交通流特征,微观模型更多考虑待疏散人员的个体行为差异,旨在模拟预测过程,或评估影响疏散过程的各种参数。如Pel等总结了以往学者的研究成果,认为重复的二进制逻辑模型适用于是否参与撤离以及开始撤离时间的预测,混合路径选择模型适用于疏散路径选择,该模型将疏散人员的行为与个人信息综合到EVAQ模型当中[7-8]。Chen等提出采用庞特里亚金最小值原理获得最短的应急时间,并动态考虑交叉口容量,但此方法仅适用单个个体[9]。何大治等采用几何方法规划人员的最佳疏散路径,此方法突破传统网格法限制人员只能在网格中移动,充分考虑人员的运动方向,具有很大的灵活性,设计人员个体和障碍物、人员个体之间的碰撞检测方法,以移动路径最短为目标,规划人员疏散方向和路径[10]。Zheng等基于粒子群优化算法(PSO)改进其更新规则,既考虑个体行为的影响又考虑环境相互作用,使得距离安全出口最近的人员先疏散,但是当出现拥堵时,安排人员在拥堵区附近等待,这将有可能发生争抢有效道路资源的问题[11]。Uno及Kashiyama利用多智能体模拟器“artisoc”开发应急疏散模拟软件,用以分析疏散过程的演变规律[12]。最优疏散调度算法中交通模拟模型和最小风险交通分配算法不可或缺。DYNASMART-P是一个在智能网络设计,规划,评估,交通仿真等领域有效的工具。疏散模型中安全区域需要被指定,但是分配给安全区的交通流是不能预设,因此,将所有指定的安全区域聚合到一个虚拟安全地区。同时在最小风险流建模中聚合区域以利于多个交通分析区(TAZ)被指定为一个安全区。实验表明,所提出的方法在非预期极端事件中为大规模的紧急疏散管理提供了一个重要规划[13]。
总结来看,宏观模型与微观模型侧重点不同,前者强调统一疏散方案的制定,后者强调疏散个体在整个疏散过程中的表现与相互影响。Chen采用基于智能体的微观模拟技术,研究同时和分阶段疏散策略对加尔维斯顿岛飓风疏散的效率。实验结果显示同时疏散不一定获得有效的疏散方案而最有效的分阶段疏散能够减少约1 h的疏散时间[14]。也有实验表明,如果分阶段疏散合理地应用,能够显著减少疏散和延迟时间[15]。Li等设计实验场景比较同时疏散与分阶段疏散效率。在各个场景中,同时疏散需要的时间比分阶段疏散少。现实中,同时疏散无法总是保证所有疏散者能够自发地移动,但分阶段疏散是可控制的。并且随着疏散规模的增大,分阶段疏散花费的时间越接近同时疏散[5]。而本文提出的方案正是为解决大规模疏散问题,因此,着重分析利用虚拟结点法完善分阶段算法在多安全出口情况下的适用性问题。
2 问题定义
本文采用典型的结点-弧段模型描述道路网络[16]。即设G= A,N 表示一个道路网络,其中A={a1,a2,…,an}表示对应 n条道路的弧段集,N={n1,n2,…,nm}表示对应m个道路交叉口的结点集。本文将待疏散人员根据其所处的地理位置聚合到道路网络中的各结点并将同一结点的疏散人员归为一组,然后由该结点进入道路网络中。相关变量定义如下:
δ表示疏散组的数量。
Nexit表示安全出口结点(虚拟结点法将新增的虚拟结点对应此结点)。
t0表示疏散命令发出时刻。

routev=表示疏散组v的疏散路径,共k条弧段,由以上定义可知,nv0和 Nexit分别对应routev中a和a二者的终点。
(3)用于疏散的道路具有近似的通行容量。
(4)无背景交通流。
根据以上变量及假设,总疏散时间TET定义如下:

TET表示从t0开始到第δ个疏散组完全通过Nexit过程中耗费时间最长一组的疏散时间。疏散方案的目的在于有组织地快速撤离人员,因此,本文将总疏散时间TET的长短作为评价方法适用性的标准。
3 方法
3.1 分阶段算法
当突发事件的影响范围较大,需要疏散居民较多时,同时疏散会使得短时的交通需求过大,而疏散路网容量是相对固定的,因此,疏散道路会处于饱和或者超饱和状态,疏散车流拥挤十分严重,甚至会堵塞很长时间,总的疏散时间也会相应延长。因此,分阶段算法的目的在于确保总疏散时间最小化的同时能够使得整个道路网络不发生拥堵,人员能够有组织、有序撤离。因此,当公式(1)中TET获得最小值时,总疏散时间达到最小。然而,对于给定疏散组v,t0和已知,最小化即可达到算法目的。根据变量定义,疏散组选择到达安全出口的最短路径即最小化在此算法中采用Dijkstra最短路径算法[17]计算v到Nexit的最短路径routev。因此,最小化成为算法的目标。理论上,当最接近Nexit的疏散组到达Nexit后,其他的疏散组连续地跟随进入Nexit直到所有疏散组完成疏散是最优的方案,但现实实现依赖于被疏散者的分布和道路网络的空间配置。


一旦算法为所有疏散组设置好开始撤离时刻和撤离路径,就告知疏散者,避免人员在交叉口发生拥堵,同时也避免人员在遇到拥堵时发生争抢有效道路资源从而延长整个疏散过程。但此算法只能满足一个安全出口的情况,有一定的局限性。因此,本文在上述算法的基础上结合了虚拟结点法以适应多安全出口情况。
3.2 虚拟结点法
3.1节中介绍的分阶段疏散算法尚不支持多出口情形,可利用虚拟结点修改网路结构以突破此局限性,将多源多汇问题转换为多源单汇,也更容易满足先进先出(FIFO)原则。此方法的目的在于减少网络中所有疏散者的总出行成本[18]。具体步骤如下:首先,在网络中添加一个虚拟结点,即网路流问题中的汇,并将它作为足以容纳网络中所有疏散者的最终安全出口,再将所有已知安全出口通过虚拟弧段连接到该虚拟结点,从而所有待疏散人员就作为该“汇”的输入[1]。其中,所有安全出口在连接到虚拟结点后将作为路网中的待疏散容量为零的普通结点,虚拟弧段的长度为零,即通过时间为零。然后,将其应用到分阶段算法中以解决道路网络的人员疏散问题。如图1所示,在原有道路结点图层中增加一个虚拟结点 D*,将实际安全出口D1,D2连接到 D*,再次构建新的拓扑关系。疏散人员的最短疏散路径即为出发结点到D*的最短路径。在重建拓扑关系之后,道路网络中只有一个安全出口,多安全出口问题转化为单个安全出口问题,满足分阶段算法的适用条件,因而可对整个道路网络应用分阶段算法。
4 适用性分析
本文提出的方法采用C#语言在Microsoft Visual Studio 2010开发平台,酷睿2 2.0 GHz CPU,2 GB内存环境下实现,并对其适用性进行分析。实验设置如表1所示的6种多出口情景,随机生成均匀分布和不均匀分布2类人口分布,并以图2所示的包含247个结点,312条道路的某道路网络为例,疏散者平均速度为10 m/s,采用虚拟结点法进行模拟疏散。

图1 虚拟结点法示意图

表1 实验情景定义
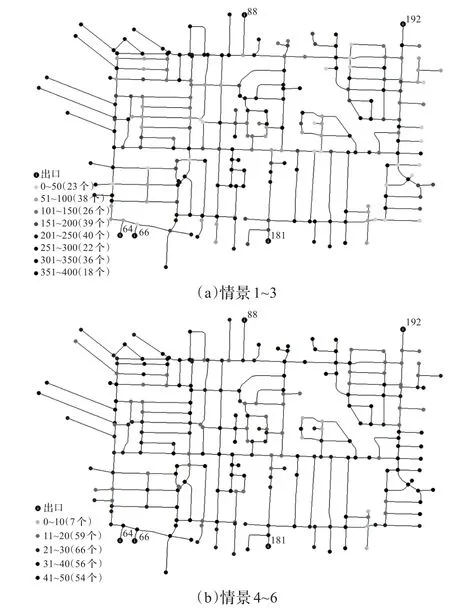
图2 道路网络、出口和人口分布图
图3表示各实验情景下以远离安全出口的疏散组先撤离原则进行疏散时出口被疏散小组占用情况,实验结果在0.58~1.2 s之内获得。出口被占用情况间接反映出总疏散时间。最后占用出口的疏散组结束占用的时刻越晚,总疏散时间越长,方法适用性越差。反之,总疏散时间越少,方法适用性越好。从图3中还可以获得以下几点信息。
首先,横向比较图3中各场景,情景1,情景4中各出口被占用时间差距最大。在情景1中,通过出口66,64的人数分别为37 186和10 360,出口66疏散的人数是出口64的3.589倍。而在情景4中,通过出口66,64的人数分别为5 795和1 422,出口66疏散的人数比出口64多出了3.075倍,各出口疏散的人数分配十分不均。结合图2出口位置分布可知两个安全出口地理位置集中,且分布在路网的一角,而各个疏散组按到虚拟结点的最短路径选择安全出口,导致多数疏散组选择某一距离更近的出口(出口66)却不选择通往空闲出口(出口64)。因此在有组织疏散人群的前提下,部分疏散组的出发时间被延迟,最终导致疏散时间的明显增长。

图3 各情景出口被占用情况
其次,纵向观察图3中各场景,情景2、3、5、6各个出口被占用时间较为均匀。上述情景中,按各情景中出口编号顺序,疏散人数比例依次为:1.053∶1,1.520∶1.342∶1.212∶1,0.994∶1,1.199∶1.106∶1∶1.093,由此可见,各安全出口需要疏散的人群总数约相当。且安全出口分散地分布在路网边缘,因此,能够充分利用两个安全出口进行疏散。
此外,情景3下各出口疏散人数比例比情景2、5、6人数大,因道路网络中结点的人数随机分布,使得在情景3下通往出口64的人口数较其他出口更多,导致各出口需疏散的人口数不均,被占用时间差距大,从图3中也可以得到印证。
图4~6为情景1~3下以远离安全出口的疏散组先撤离为原则的一系列时刻的快照图。该系列时刻分别为第 2 200 s,2 300 s,2 400 s,2 500 s,2 600 s,2 700 s。不同颜色的结点表示聚集在此出发结点并等待出发时刻的各组疏散人员,不同颜色的线段表示正在撤离的各疏散组,线段的长度表示疏散组的大小,标有编号的结点表示安全出口。如图4~6可知,开始出发的疏散人员能够有序地通往各自的安全出口,而未开始疏散的人员则在原地等待其开始疏散的时刻,并未出现交叉口拥堵的情况。
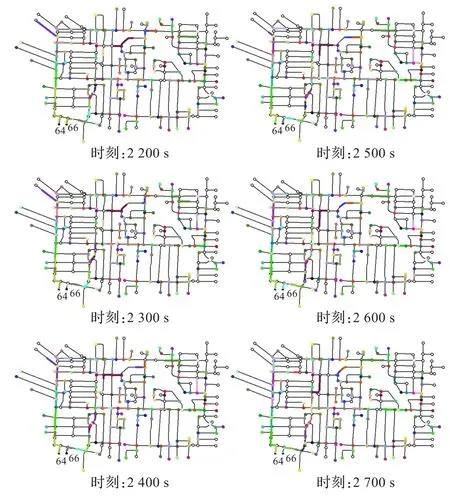
图4 情景1下疏散过程系列快照图

图5 情景2下疏散过程系列快照图
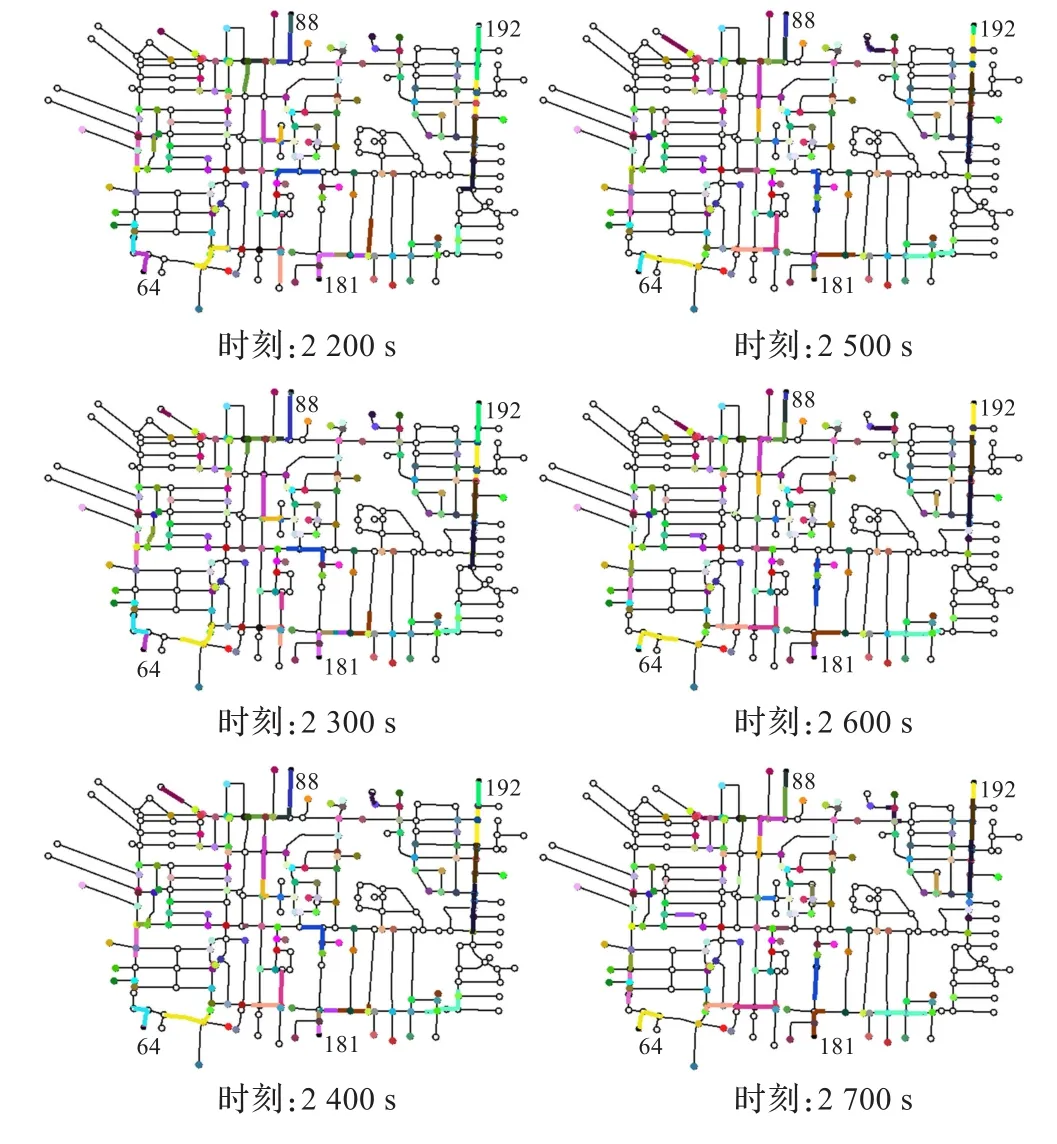
图6 情景3下疏散过程系列快照图
由实验结果可知虚拟结点法在情景2、3、5、6这些出口分布较为分散且各出口待疏散的总人口数相当的情况下,各个出口的被占用时间差距较小且最后占用出口的疏散组结束占用的时刻较其他场景早,总疏散时间也缩短,具有较好的适用性。然而,对于情景1、4这种出口分布较为集中,且各出口待疏散人口差距显著的情景虚拟结点法的适用性较差。
5 结论
本文在已有的分阶段疏散算法基础上进行完善,结合虚拟结点法以解决多个安全出口的人群疏散问题,同时分析虚拟结点法的适用性。虚拟结点法即在原有道路结点图层中新增一个虚拟结点作为最终安全出口,把原有实际出口作为普通结点并虚拟路径将实际出口连接到该虚拟结点,重新构建拓扑关系后应用分阶段疏散算法疏散人群。同时,本文以某路网为例设置在不同总疏散人口场景下,2个安全出口距离远,2个安全出口距离近,4个安全出口均匀分布这3类不同安全出口位置分布情景进行实例验证。模拟结果显示,此方法能够有效解决大规模人群的多安全出口应急疏散。但适用性因安全出口分布和各出口待疏散的人口总数差距不同而不尽相同,虚拟结点法更适合当各个安全出口的位置比较分散,且各安全出口需要疏散的人数分配较为均匀,使得各安全出口能够接近同时完成疏散的情形。当多个安全出口较为集中,待疏散人群不能较均匀地分配到各安全出口,从而各出口不能保持大致同时处于疏散状态时,方法的适用性较差。因此,调整各安全出口通过的待疏散人群,以使多个安全出口保持大致同时在疏散状态,达到疏散时间的最优化,这部分将会是下一步需要研究的问题。
[1]Hamacher H W,Tjandra S A.Mathematical modelling of evacuation problems-a state of the art[J].Pedestrian and Evacuation Dynamics,2002:227-266.
[2]Bretschneider S,Kimms A.A basic mathematical model forevacuation problemsin urban areas[J].Transportation Research Part A:Policy and Practice,2011,45(6):523-539.
[3]Yamada T.A network flow approach to a city emergency evacuation planning[J].InternationalJournalofSystems Science,1996,27(10):931-936.
[4]Liu Y,Lai X,Chang G L.Cell-based network optimization model for staged evacuation planning under emergencies[J].Transportation Research Record:Journal of the Transportation Research Board,2006,1964:127-135.
[5]Li X,Huang B,Liu Z J,et al.A novel method for planning a staged evacuation[J].Journal of Systems Science and Complexity,2012,25(6):1093-1107.
[6]Saadatseresht M,Mansourian A,Taleai M.Evacuation planning using multiobjective evolutionary optimization approach[J].European JournalofOperationalResearch,2009,198(1):305-314.
[7]Pel A J,Bliemer M C J,Hoogendoorn S P.A review on travel behaviour modelling in dynamic traffic simulation models for evacuations[J].Transportation,2012,39(1):97-123.
[8]Pel A J,Hoogendoorn S P,Bliemer M C J.Evacuation modeling including traveler information and compliance behavior[J].Procedia Engineering,2010,3:101-111.
[9]Chen Y,Xiao D.Emergency evacuation model and algorithms[J].Journal of Transportation Systems Engineering and Information Technology,2008,8(6):96-100.
[10]何大治,王长波,谢步瀛.基于几何方法的人员疏散最佳路径[J].工程图学学报,2006,27(5):23-28.
[11]Zheng Y,Chen J,Wei J,et al.Modeling of pedestrian evacuation based on the particle swarm optimization algorithm[J].Physica A:StatisticalMechanics and Its Applications,2012,391(17):4225-4233.
[12]Uno K,Kashiyama K.Development of simulation system for the disaster evacuation based on multi-agent model using GIS[J].Tsinghua Science& Technology,2008,13:348-353.
[13]Chiu Y C.Traffic scheduling simulation and assignment for area-wide evacuation[C]//7th International IEEE Conference on Intelligent Transportation Systems,2004:537-542.
[14]Chen X.Microsimulation of hurricane evacuation strategiesofGalveston Island[J].The ProfessionalGeographer,2008,60(2):160-173.
[15]Chien S I,Korikanthimath V V.Analysis and modeling of simultaneous and staged emergency evacuations[J]. Journal of Transportation Engineering,2007,133(3):190-197.
[16]Sheffi Y.Urban transportation networks:equilibrium analysis with mathematical programming methods[M].Englewood Cliffs,NJ:Prentice Hall,1985.
[17]Dijkstra E W.A note on two problems in connexion with graphs[J].Numerische Mathematik,1959,1(1):269-271.
[18]Han L D,Yuan F,Chin S M,et al.Global optimization of emergency evacuation assignments[J].Interfaces,2006,36(6):502-513.
XIE Jun1,WAN Qing2,ZHANG Chi3,LI Qiang4,5,LI Xiang1
1.Key Laboratory of Geographic Information Science,Ministry of Education,East China Normal University,Shanghai 200241,China
2.Institute of Geographical Sciences and Natural Resources Research,Chinese Academy of Sciences,Beijing 100101,China 3.Xinjiang Institute of Ecology and Geography,Chinese Academy of Sciences,Urumqi 830011,China
4.Unit 95806 of PLA,China
5.School of Architecture,Tsinghua University,Beijing 100084,China
The expansion of city scale and ceaseless rise of population density are advanced by urbanization process.It’s an urgent problem to make an effective emergency evacuation plan with the purpose of evacuating pedestrian to safe places fast and orderly when danger happens.Many researches are done on this field,and virtual node approach is applied to network flow problem a lot.The staged evacuation algorithm based on road network for single exit is combined with virtual node approach which is applied to multiple exits evacuation planning,with the purpose of analyzing applicability of virtual node approach in this paper.The simulation results show that the approach can organize massive pedestrian to safe places orderly and fast.
multiple exits;virtual node approach;emergency evacuation;staged evacuation
城市化进程的迅速推进促使城市规模日益扩大、人口密度不断提高,制定一个有效的应急疏散方案,使得人员在存在危险时快速且有序地撤离到安全场所,已经成为迫切需要解决的问题。目前已有一些研究成果,而虚拟结点法在网络流中已有较多应用。结合基于道路网络的单出口分阶段疏散算法,将虚拟结点法应用在多出口疏散方案中,旨在对虚拟结点法的适用性进行分析。模拟结果显示,该方法能够有序、快速地组织大规模人群到安全场所。
多安全出口;虚拟结点法;应急疏散;分阶段疏散
A
U491
10.3778/j.issn.1002-8331.1301-0194
XIE Jun,WAN Qing,ZHANG Chi,et al.Applicability analysis for virtual node approach to evacuation plan with multiple exits.Computer Engineering and Applications,2014,50(23):245-250.
国家高技术研究发展计划专项研究基金(No.2013AA122302);华东师范大学科研创新基金资助课题;国家自然科学基金(No.41271441);上海市自然科学基金(No.11ZR1410100)。
谢君(1988—),女,硕士生,研究领域为空间分析与建模;万庆(1964—),男,研究员,研究领域为空间数据的组织与表达;张弛(1973—),男,研究员,研究领域为城市地理信息系统;李强(1973—),男,高级工程师,研究领域为地理过程模拟;李响(1975—),通讯作者,男,博士,教授,研究领域为空间分析与建模。E-mail:xli@geo.ecnu.edu.cn
2013-01-18
2013-03-11
1002-8331(2014)23-0245-06
CNKI网络优先出版:2013-04-08,http://www.cnki.net/kcms/detail/11.2127.TP.20130408.1646.006.html
