基于WSN的数据融合在水质监测中的研究

张明阳，沈明玉

合肥工业大学 计算机与信息学院，合肥 230009

基于WSN的数据融合在水质监测中的研究

张明阳，沈明玉

合肥工业大学 计算机与信息学院，合肥 230009

1 引言

无线传感器网络（Wireless Sensor Network，WSN）是近几年来兴起的一个热点研究领域。如果把WSN应用到水质监测领域，再结合其他相关学科知识建立水质监测体系，可以实现水质监测的自动化、智能化[1]。传统的水质监测体系中，通常都是用大量的传感器来监测每个相关参数，通过无线网络通信将监测数据传送到监测系统的数据中心服务器，数据中心服务器再对接收到的各类传感器所采集的数据分别进行处理，这样不仅导致网络数据传输量非常庞大，而且切断了各类传感器间的信息关联，丢失了信息之间有机组合所包含的一些特征。数据融合技术的研究，为解决这一问题提供了方法。

2 研究背景

数据融合技术因其在多传感器信息处理领域的突出优点，现在已经成为国内外研究的热点。其基本思想是将具有一定冗余度的多源数据进行融合，减少数据的传输量，节约传感器节点的能量，并将多源信息在一定准则下加以自动分析、综合，按需完成评价及决策任务。许多学者已经在这方面研究出了大量的研究成果[2-8]，例如文献[4]的作者证明了多传感器数据融合的估计效果要比任何一个单一传感器的估计效果好。

目前，研究多传感器数据融合的算法已经很多，大致可以归纳为两大类。一类是基于随机理论的一些算法，主要有加权平均法[5]、贝叶斯估计法、D-S证据法等；一类是基于人工智能理论的一些算法，主要有人工神经网络法、模糊推理法[6]、粗糙集理论法等。在许多应用领域中依据领域内的具体背景，许多成熟有效的数据融合方法已经被研究者们应用，解决了许多实际问题[7-8]。本文在自适应加权理论和模糊综合评价理论的基础上，通过在水质监测的应用背景下，研究基于WSN的多传感数据融合。

3 水质监测体系的数据融合模型

数据融合技术研究通常是与具体研究背景相关的。在WSN的技术平台下进行水质监测数据的融合，其显著特点是具体研究背景有高度的复杂性和综合性。图1是某一局部监测区域网络拓扑结构示意图，A1、A2、…、An为水下传感器节点，A为水面传感器节点，即水下节点 A1、A2、…、An的簇头节点，部署在水下的节点采集数据，通过水声通信[9]方式传输数据到水面节点；部署在水面的节点，一方面与水下节点之间通过水声通信方式通信，另一方面直接以GPRS通信或其他无线通信方式将监测数据传输到基站（远程数据中心）。

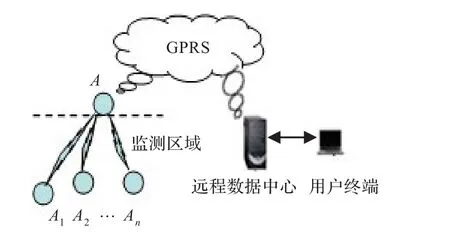
图1 水质监测网络拓扑结构图

结合水质监测的研究背景，以及相应种类传感器的感知能力，选择5类既有相互联系又比较有代表性的化学指标进行监测[10]，即选择溶解氧（DO）、化学需氧量（COD）、氨氮（NH3-N）、总氮（TN）和总磷（TP）共5项水质因素，并将相应种类传感器作为监测网络的水下传感器节点。

由图1可以看出，整个监测体系属于层次型网络。针对监测网络的层次型结构，结合水质监测的特殊性，可以相应地设计出两级数据融合模型：在水面节点，通过自适应加权理论进行第一级数据融合；在远程数据中心服务器，通过模糊综合评价理论进行第二级数据融合，其结构层次如图2所示。

图2 数据融合层次示意图

在第一级融合过程中，将簇内同类型传感器获得的数据加以融合处理，得到被监测对象更加精确的监测值；在第二级融合过程中，远程数据中心将从监测区域接收到的各类监测数据进行综合分析，多源信息融合后转化成关于被测区域水质的更可靠、更准确的状态描述。

4 自适应加权理论

同一簇内各个传感器由于彼此之间的测量精度不同，以及所在环境中噪声等因素影响，各个传感器所得数据往往与真值之间存在较大偏差，需对同一簇内同类型传感器监测数据加以融合处理，以防止个别传感器节点数据误差过大而造成最后监测结果失真严重。应用在水质监测中的传感器，也同样存在需要进行数据融合的问题。鉴于水质监测的研究背景，选用自适应加权理论在监测区域在簇头节点内将簇内节点的监测数据进行融合，即在总均方误差最小这一判决条件下，对各传感器节点的监测数据自适应地配以不同的权值（最优加权因子），使得融合结果达到最优。图3是采用自适应加权理论进行数据融合的示意图。

图3 自适应加权数据融合示意图

式中，Wi为第i个传感器的加权因子。而且：则融合结果的总均方误差为：

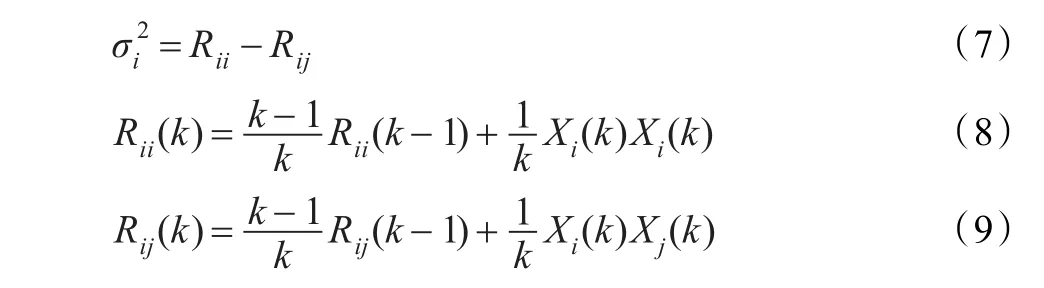
由式（7）、（8）、（9）可知，根据一组传感器的监测数据，可以递推计算法出各传感器监测数据的方差。

于是，可以根据概率论相关理论继续进行递归推导。将测量值的均值计算公式：

代入到均方差值计算公式：

式（12）即为传感器(k+1)时刻的方差递推计算式，其作用可以用于实时计算测量数据的方差。将计算所得的方差值代入式（4）即可得到各传感器自适应加权值，从而由式（1）得到融合结果。

5 模糊综合评价理论

对来自多种异类传感器所感知的数据，在一定数学理论和准则下进行多方面、多级别的综合分析处理，获得单传感器所无法获得的具有综合意义的信息，这种把多种信息进行交融的过程即是异类多传感器数据融合，亦称多源信息融合[12]。研究在水质监测中基于WSN的数据融合，其主要目的是通过融合多种评价因子以获得所监测水体的水质综合状况，目前在此研究领域常用的理论主要是模糊数学学科相关理论。鉴于应用于水质监测的远程数据中心服务器的数据处理能力较强，所以本文在模糊综合评价理论的基础上，改进部分计算过程，形成更加能够准确反映水质的方法，即采用模糊综合评价指数作为数据融合结果。

参照《地表水环境质量标准（GB3838-2002）》[13]，假设监测水体质量的因素所组成的集合为：U={u1，u2，…，un}，其中 u1，u2，…，un为参与评价的 n 个水质因素的数值；水体质量的评价集合为：V={v1，v2，…，vm}，其中 v1，v2，…，vm为m个水质评价标准。

被考虑的n个因素构成了一个论域V，需要在论域V上模糊地刻划各因素在评价中所起的作用，这样考虑各因素在模糊综合评价中影响轻重程度的过程是一种加权处理过程。决定各类评价因子对综合评价的权重，本文采用在各自超标倍数的基础上加以处理的方法[14]，计算表达式如下：

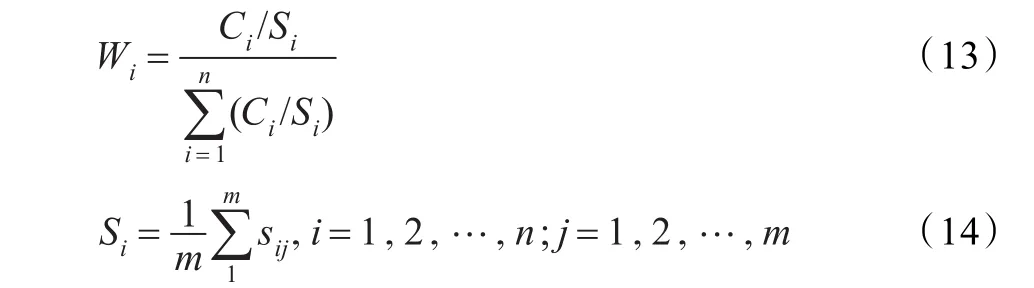
式中，Sij为第i类水质因素在 j级水质的标准值；Si为第i类水质因素的浓度标准值的算术平均值；Wi为第i类水质因素的权重值。Ci为第i类水质因素的浓度值。由《GB3838-2002》可知，一般情况下各因素的监测值相对于水质标准的超标倍数越大对水体综合评价的贡献率就越大，权重也就越大；但对于某些因素却相反，那么在确定其权重值时取其倒数。将各单项权重值进行归一化处理，可以得到权重矩阵W={W1，W2，…，Wn}。

建立一个从U到V的模糊映射 f:U→V，∀ui∈U，由 f诱导出模糊关系，得到模糊关系矩阵R，以确定因素 Ui(i=1，2，…，n)对评价标准集元素 Vj(j=1，2，…，m)的隶属度。本文采用升、降半梯形函数法来确定隶属函数。如公式（15）：

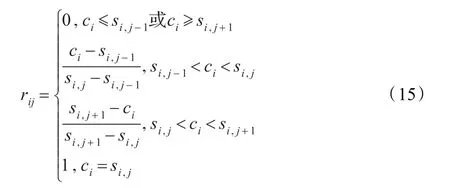
根据隶属函数公式（15）计算出各单因素的隶属度，将n个单因素的模糊隶属度进行归一化处理，构成了模糊关系矩阵，即Rn×m={rij}。如下：

该模糊关系矩阵R中，rij表示第i个因素对第 j级质量标准的隶属度。

在模糊综合评价理论中，模糊综合评价模型的选择很重要，不同的综合评价模型能够产生不同的评价效果。将权重矩阵W和模糊关系矩阵R进行模糊矩阵的合成运算Y=W·R，得到矩阵Y，一种常用方法是单因素决定模型，其中的计算过程即为：这是模糊数学中“取小取大计算”方法，容易丢失信息，甚至引起综合评价的失效[15]。本文根据模糊综合指数模型[16]，用经典线性代数中矩阵乘法来改进式（17）的计算过程，即

通过计算Y=W·R得到综合评价矩阵Y后，单因素决定模型按照“最大隶属度”原则取Y向量中的最大量，即

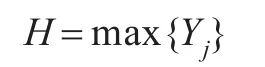
本文根据《GB3838-2002》中将水质分为5类的原则，建立水质标准类别向量，即

将水质标准类别矩阵ST与综合评价矩阵Y进行矩阵乘法的合成运算，得出模糊综合指数FCI（Fuzzy Colligation Index），即

该结果即为根据模糊综合评价理论，进行多传感器数据融合后的结果。模糊综合指数FCI反映出传感器采集到的各类数据的综合效应，能够比较客观地反映水质状况。

综上，模糊综合评价理论的算法流程可概括描述如下：

6 实验结果及分析

实验选用巢湖流域的4条水源河流入湖口处的水样作为监测对象，分别标记为A、B、C、D，用实验选用的5类传感器进行水质监测实验，搭建实验平台。

在A处水样的实验过程中，布局簇内水下节点 A1、A2、A3以及簇头水面节点 A0，水下节点 A1、A2、A3监测水体内溶解氧（DO），并在水上节点 A0内进行数据融合。例如，实验中一次监测实验中测得DO：XA1=5.511，XA2=5.057，XA3=5.712，节点方差分别为：σ21=0.05，σ22=0.1，σ23=0.2，所 对 应 的 权 值 为 W1=0.571 5，W2= 0.285 7，W3=0.142 8，融合结果 XA=5.410。如此实验50次，所得结果如图4所示，以此所得数据来分析实验中第一级数据融合的作用。

图4 对A处水样DO的50次监测数据

图4结果显示，个别节点（如 A3）监测数据波动较大，通过自适应加权理论进行数据融合后，监测数据波动较大的节点并未对实验结果产生较大影响。

将样本数据的算术平均值作为测量结果，是一种常用的降低测量误差的方法，其可以看作是样本数据在相等权值的条件下加权融合的过程。图5所示为算术平均值计算法与自适应加权计算法的融合结果，很清楚地看出，自适应加权计算法的融合结果明显优于算术平均值计算法。

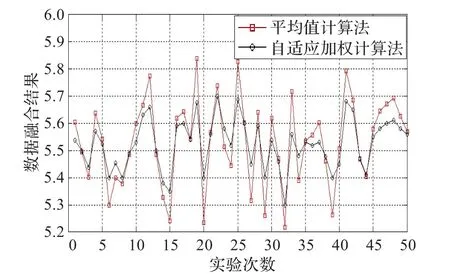
图5 算术平均值计算法与自适应加权计算法的性能比较

通过自适应加权理论进行第一级数据融合，所得到的是水样各项评价因子的同类型数据融合结果。表1所示，即为一次实验中4条河流入湖口处水样通过第一级数据融合所得到的结果。

表1 第一级数据融合结果

将第一级数据融合结果通过模糊综合评价理论，进行第二级数据融合。表1所示的数据，经第二级数据融合后，所得到的数据融合结果如表2所示。

表2 第二级数据融合结果

通过模糊综合评价理论将不同类型数据进行融合，其结果是关于水质的模糊综合指数，是对水样各项评价因子进行综合分析的融合结果，结合水质标准等级[13]，FCI指示出水体水质的全局状态评价值。

模糊综合指数模型，是一种比较理想的异类数据融合模型，与常见的单因素决定理论模型相比，其优势在于能够充分考虑到各项评价因子的作用，表3所示是本次实验表1所示数据采用单因素决定模型进行数据融合的结果。

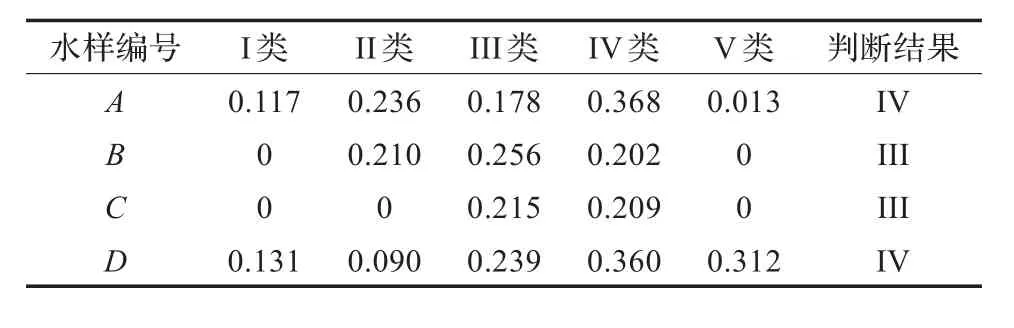
表3 单因素决定模型的数据融合结果

对比表3和表2的数据可以看出，单因素决定模型，往往会过度突出某一项偏高的评价因子的作用，如A处水样中化学需氧量（COD）偏高，导致对水体水质的判断结果为IV级；同时也会过度消弱某一项偏低的评价因子的作用，如D处水样中氨氮（NH4+-N）很低，采用单因素决模型所得到的结果却是IV级。模糊综合指数模型能够充分体现各个参评因子对整体综合评价的作用，其评价结果是各个参评因子综合作用的结果，所以，在第二级数据融合过程中，采用模糊综合指数模型进行数据融合，能够大大减小由于单一评价因子信息量的局限性引起的误判和错判，增加水质监测的可信度，提高并改善了监测系统的性能。

7 结束语

本文根据水质监测的特殊性，在解决水质监测应用平台内水下节点不能直接通过水声通信与远程数据中心（基站）进行通信的问题时，巧妙使用自适应加权理论和模糊综合评价理论相结合的方法，设计出一种针对水质监测的两级数据融合模型。构建无线传感器网络实验平台进行实验验证，对于同类型传感器使用自适应加权理论进行数据融合，以提高监测数据的准确性；对不同类型的监测数据，使用模糊综合评价理论，将多传感器在监测区域获得的一组评价因子进行模糊数据融合，所得结果具有更高的可信度，提高并改善了监测系统性能。

[1]王骥，徐国保，沈玉利.基于无线传感器网络的海水检测系统设计[J].通信技术，2008，41（12）：385-387.

[2]Wen Chenglin，Pan Quan，Zhang Hongcai，et al.Multi-sensor single modelmulti-scale fusion[J].ControlTheory and Applications，2000，17（6）：841-864.

[3]文成林.多传感器单模型动态系统多尺度数据融合[J].电子学报，2001，29（3）：341-345.

[4]周福娜，周梅，文成林.多传感器数据融合效果分析[J].河南大学学报，2003，33（2）：33-36.

[5]翟翌立，戴逸松.多传感器数据自适应加权融合估计算法的研究[J].计量学报，1998，19（1）：69-75.

[6]党宏社，韩崇昭，王立琦，等.基于模糊推理原理的多传感器数据融合方法[J].仪器仪表学报，2004，25（4）：527-530.

[7]付华，沈中和，孙红鸽.矿井瓦斯监测多传感器信息融合模型[J].辽宁工程技术大学学报，2005，24（2）：239-241.

[8]孙红鸽，臧义，曹毅，等.模糊数据融合在多传感器环境监测中的应用[J].工矿自动化，2009，35（8）：22-24.

[9]许克平，许天增，许茹，等.基于水声的水下无线通信研究[J].厦门大学学报：自然科学版，2001，40（2）：311-319.

[10]吴邦灿，费龙.现代环境监测技术[M].北京：中国环境科学出版社，2005.

[11]李莉，高冰.自适应加权数据融合加权因子的动态调整[J].战术导弹技术，2011，5（3）：109-111.

[12]杨露菁，余华.多源信息融合理论与应用[M].2版.北京：北京邮电大学出版社，2011.

[13]中华人民共和国环境保护总局.GB3838-2002地表水环境质量标准[S].北京：中国环境科学出版社，2002.

[14]王罗春.环境影响评价[M].北京：冶金工业出版社，2012.

[15]王道勇.模糊综合评判的失效与处理[J].工科数学，1994，10（1）：45-49.

[16]邓峰.水质评价的一种新方法——模糊综合指数法[J].中国环境科学，1991，11（1）：63-66.

ZHANG Mingyang,SHEN Mingyu

College of Computer and Information,Hefei University of Technology,Hefei 230009,China

Multi-sensor data fusion is a kind of data processing method.It refers to fusing data from a large number of sensors for various and multi-level treatment,creating a sort of information more meaningfully,while this sort of information is almost impossible to get for any single sensor.Researching of WSN-based data fusion in water quality,it puts forward a multi-sensor data fusion model of two levels,suitable for water quality monitoring,which combines self-adaptive weighted theory and fuzzy comprehensive evaluation theory together.Processing the same type of data collected from monitored area,it uses the self-adaptive weighted theory,while it uses the fuzzy comprehensive evaluation theory for different types of data.The experimental result,made by lake water sample to Chaohu Basin,shows that using the model can effectively reduce the amount of data traffic,reduce the rate of deviation,improve the credibility of monitoring result.

Wireless Sensor Network（WSN）;water quality monitoring;data fusion;self-adaptive weighted theory;fuzzy comprehensive evaluation theory

多传感器数据融合是一种数据处理方法，可以对来自多个传感器的数据进行多方面、多层次的处理，从而产生更有意义的信息，而这种信息是单一传感器难以获得的。通过在水质监测应用背景下研究基于WSN的数据融合，提出了一种针对水质监测的两级数据融合模型：处理传感器所采集到的监测数据时，对于同类型的数据采用自适应加权理论进行第一级数据融合；对于不同类型的数据采用模糊综合评价理论进行第二级数据融合。对巢湖流域水样监测的实验结果表明，这种采用自适应加权理论和模糊综合评价理论相结合的数据融合模型，能够有效降低监测网络的数据传输量，降低监测数据的误差，提高水质状态监测的可信度。

无线传感器网络（WSN）；水质监测；数据融合；自适应加权理论；模糊综合评价理论

A

TP393

10.3778/j.issn.1002-8331.1301-0123

ZHANG Mingyang,SHEN Mingyu.Research of WSN-based data fusion in water quality monitoring.Computer Engineering and Applications,2014,50（23）：234-238.

合肥工业大学博士专项基金（No.GDBJ2009-005）。

张明阳（1988—），男，硕士研究生，研究领域：无线传感器网络；沈明玉（1962—），男，博士，副教授，硕士生导师，CCF高级会员，研究领域：无线网络、网络信息安全。E-mail：anhuizhmy@163.com

2013-01-14

2013-02-28

1002-8331（2014）23-0234-05

CNKI网络优先出版：2013-04-08,http://www.cnki.net/kcms/detail/11.2127.TP.20130408.1648.011.html