Matlab在《高等数学》中的应用*

吴 磊

(包头师范学院 数学科学学院，内蒙古 包头 014030)

1 引言

目前，高等数学已成为我校一门十分重要的基础课程。随着越来越多的学生选择考研，高等数学尤为重要。然而，我们可以通过引入数学软件Matlab简化并解决那些较为复杂的问题，更便于学生理解。

Matlab是由美国Mathworks公司发布的一种数学软件。目前，国内的各大学陆续将Matlab软件正式列入研究生和本科的教学计划。Matlab软件与数学的结合简化许多数学计算。

我们先来介绍一下Matlab的优点：

(1)Matlab的工作界面简单，编程环境提供了比较完备的调试系统，并且程序不必经过编译可以直接运行，能够及时报告错误并进行错误原因分析。

(2)Matlab具有强大的科学计算和数据处理能力。Matlab是一个包含大量计算算法的集合，拥有600多个工程中要用到的数学运算函数，这些函数包括从最简单基本的函数到多维数组的计算。

(3)Matlab具有出色的图形处理能力。Matlab具有方便的数据可视化功能。能将二维和三维的可视化，图像处理，可用于科学计算和工程绘图。

2 Matlab在高等数学中的应用

2.1 Matlab在极限中的应用

极限是高等数学中最重要、最基本的概念，极限方法是研究变量的一种基本方法。极限思想是“在自变量的某个变化过程中，对应的函数值无限接近于某个数。”求极限的方法多种多样，如：重要极限，洛必达法则等。但对于某些比较复杂的求极限，利用Matlab软件更为简单。

在Matlab的命令窗口输入：

>> syms x

>> y=((sin(x)-sin(sin(x)))*sin(x))/(x^4);

>> f=limit(y,x,0)

f =1/6

在Matlab的命令窗口输入：

>> syms x y

>> z=log(x+exp(y))/(x+y);

>> f1=limit(z,x,1);

>> f2=limit(f1,y,0)

f2 =log(2)

得到的结果为：极限值等于ln2

2.2 Matlab在积分中的应用

积分主要处理变量“无限连续求和”问题。在教学过程中我们主要介绍一元函数的积分，包括一元函数积分的定义及求解一元函数积分的方法，但在实际生活中，二元和三元函数的积分应用更为广泛。

在Matlab的命令窗口输入：

>> syms x y

>> f=x+2*y;

>> v1=int(f,x,y^2-4,5);

>> v2=int(v1,y,-3,3)

v2 =252/5

我们先来观察直线y=x，y=4x，x=1所围成的区域，在Matlab的命令窗口输入：

>>x=0:0.1:4; %x从0到4步长0.1

>> y1=x; %变量表达式

>> y2=4*x;

>> plot(x,y1,'b-',x,y2,'M',x,1,'r-');

%在同一图中分别做y=x，y=4x，和x=1直线

>> axis([0 4 0 4]); %设置坐标

>> title('y=x,y=4x,x=1所围成区域') %加图形标题

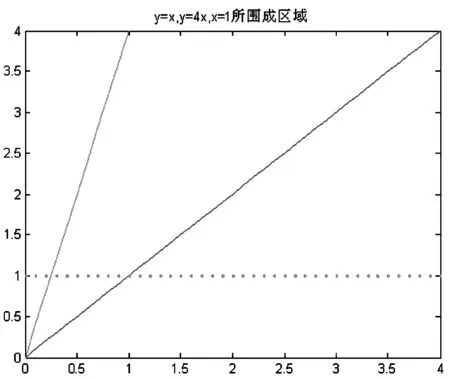
求直线的交点，在Matlab的命令窗口输入：

>> syms x y

>> y1=('y=x');

>> y2=('y=4*x');

>> [x,y]=solve(y1,y2,x,y) %求y=x和y=4x的交点，输出积分限

x =0

y =0

求二重积分值，在Matlab的命令窗口输入：

>> syms x y

>> f=exp(x+y);

>> y1=x;

>> y2=4*x;

>> fy=int(f,y,y1,y2);

>> fx=int(fy,x,0,1)

fx =1/5*exp(5)-1/2*exp(2)+3/10

>> syms x y z

>> f1=('z=0.5*(x^2+y^2)');

>> f2=('z=2');

>> [x,y,z]=solve(f1,f2,x,y,z)

x =(4.-1.*y^2)^(1/2)

-1.*(4.-1.*y^2)^(1/2)

y =y

y

z =2.

求积分，在Matlab的命令窗口输入：

>> syms x y z

>> f=x^2+y^2;

>> z1=0;

>> z2=0.5*(x^2+y^2);

>> x1=-(4-y^2)^(1/2);

>> x2=(4-y^2)^(1/2);

>> fz=int(f,z,z1,z2);

>> fx=int(fz,x,x1,x2);

>> fy=int(fx,y,0,2)

fy =16/3*pi

2.3 Matlab在微分方程中的应用

在实际问题中，方程中不只含变量和未知函数，还包括导数，我们把这样的方程称为微分方程。常见的求解微分方程有可分离变量法，齐次方程，伯努利方程等。方法比较多，针对不同题型应用不同的方法。我们通过Matlab求微分方程更简单，得到更精确的解。

在Matlab的命令窗口输入：

>> dsolve('Dy+y=(y^2)*(cos(x)-sin(x))','x')

ans =-1/(sin(x)-exp(x)*C1)

例7:求解微分方程2y″+5y′=5x2-2x-1的通解

在Matlab的命令窗口输入：

>> dsolve('2*D2y+5*Dy=5*x^2-2*x-1','x')

ans =1/3*x^3-3/5*x^2-2/5*exp(-5/2*x)*C1+7/25*x+C2

得到的结果为：

例8:求初值问题

的解。

在Matlab的命令窗口输入：

>> dsolve('D2y-3*Dy-4*y=0','y(0)=0','Dy(0)=-5','x')

ans =exp(-x)-exp(4*x)

得到的结果为：y=e-x+e4x

3 结束语

在一些较难理解、计算的高等数学知识，我们通过引入Matlab软件，使学生更容易理解，更能调动学生学习的积极性，也使学生对所学知识进行巩固。尽管Matlab在计算方面有许多优点，但高等数学还是应该以课本知识为主，Matlab只是辅助工具，Matlab只是为了帮助学生理解一些比较抽象的知识。

〔参考文献〕

[1]李东平、田强、吴培生.高等数学(上)[M].呼和浩特：内蒙古大学出版社,2010,09.

[2]王洪珂、黎彬、李可人.高等数学(上)[M].北京：教育科学出版社,2011,09.

[3]刘光旭、张桥真.高等数学(下)[M].北京：北京邮电大学出版社,2011,11.

[4]张国辉.MATLAB在高等数学中的应用探究[J].当代教育理论与实践,2009,06.

[5]张雪峰、李文林.MATLAB在高等数学中的几点应用[J].安阳师范学院学报,2009,10.

[6]李娜、仁庆道尔吉.MATLAB在高等数学教学中的应用研究[J].大学教育,2012,11.

[7]张景、石琳、张换香.MATLAB在高等数学教学中的应用[J].阴山学刊,2010,09.

[8]詹涌强.MATLAB在高等数学教学中的应用[J].新课程研究(中旬刊),2012,10.

[9]尹云辉.MATLAB在高等数学教学中的应用[J].软件导刊,2011,05.

[10]王彪.MATLAB在高等数学教学中的应用[J].计算机与数字工程,2013,08

[11]王钟斐.MATLAB在大学数学实验课程中的应用[J].计算机与数字工程,2013,09.

[12]刘蒙.MATLAB在大学数学教学中的应用[J].新课程研究(中旬刊),2014,01.

[13]朱艳科.MATLAB在大学数学教学和实验中的应用[J].广西科学院学报,2010,02.

[14]菅小艳.MATLAB在高等数学教学中的应用[J].计算机时代,2011,05.