Numerical Traveling Wave Solutionfor the General Korteweg-de Vries Equation*

GUO Zhong-zhao

(Faculty of Mathematics,Baotou Teacher's College;Baotou 014030)

1 Introduction

The well known KdV equation had been derived in 1885 by the two scientists Korteweg and de Vries to describe long wave propagation on shallow water. The KdV and the KdV-type equations not only play an important role in soliton theory, but also represent very good prospect in many applied fields such as fluid, mechanics, plasmas, crystal lattice vibrations at low temperatures, etc .

During the last few decades, the construction of exact solutions for KdV and the KdV-type equations has been done by many researchers. The Jacobian elliptic function, the powerful inverse scattering transform, the Backlund transformations technique, the Painleve analysis, the Lie group theoretical method, the direct algebraic method and the tangent hyperbolic method have been used in construction of exact solutions of KdV-type equations[1-9].Adomian decomposition method and finite difference method have been used to find numerical solution of GKdV equation[10]. Helal have studied analytically and numerically some physical problems that lead to the KdV equations and the soliton solutions have been obtained[11,12].Exponential finite difference method (EFD) has been used to find the numerical solution of KdV equation[13].

The General Korteweg-de Vries equation (GKdV) has the following form:

ut+εunux+μuxxx=0,

(1)

whereunuxanduxxxrepresent the nonlinear convection and dispersion effects.

In this work, we construct a new Exponential finite-difference (EFD) method and use it to discuss the numerical traveling wave solutions of GKdV equation. The GKdV equation we discussed is presented by Eq. (1). Specific exact solution will be determined for each value ofngiven by

(2)

2 The new exponential finite difference method

We assume thatF(u)denote arbitrary continuous differential function. Multiplying Eq. (1) by the derivative ofF(u) leads to the following equation:

That is

(3)

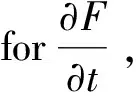
(4)

whereτis the time step. Different from Ref. [13], lettingF(u)=eu, we obtain the exponential finite difference scheme as follows

(5)

The finite differences for the derivatives have been taken as

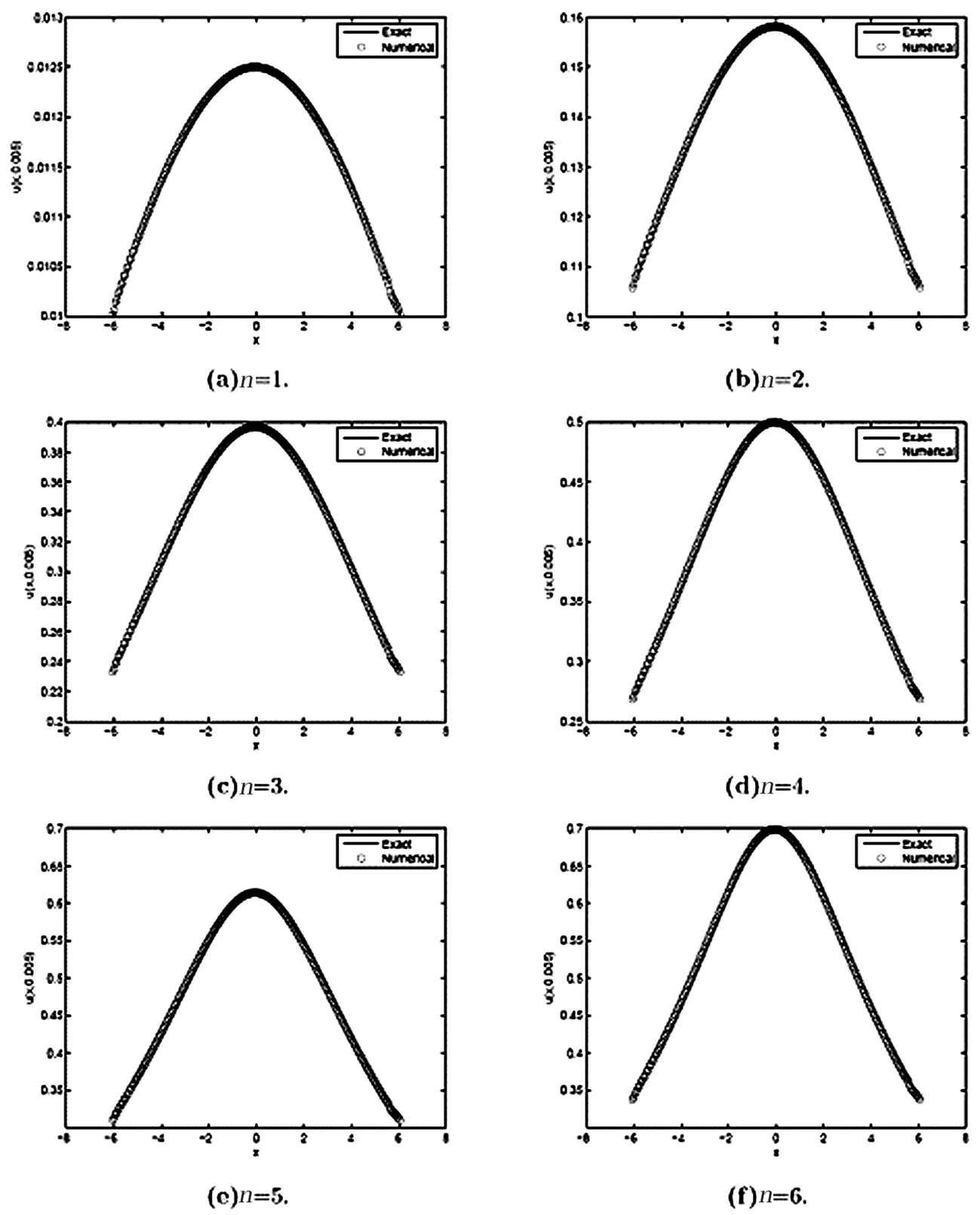
Fig.1:Comparison of exact and numercal solutions for different n at time 0.005 when c=0.025

(6)

(7)

(8)

wherehrepresents the space step. For calculation convenience, we use the initial condition

(10)

3 Numerical results and some illustrations

Letε=6,μ=1,c=0.0025in Eq. (1). Numerical solutions will be determined by Eqs. (5)-(9). All numerical computations are performed with the space steph=0.06and the time stepτ=0.0001. The EMD’s absolute errors are displayed in table 1. At the same time, Fig.1 shows the soliton solution of the GKdV equation forn=1,2，3andn=4,5,6 at t = 0.005.According to the results presented here, the EFD behaves well. EFD can be used for approximating traveling wave solutions of KdV-type equations. Comparisons of numerical solution with exact solution for differentncan be found in Fig.2 forc=0.25 Fig.3 and Fig.4 give the numerical results at time 0.5 and 1.0. The numerical results show that the EFD scheme works well.

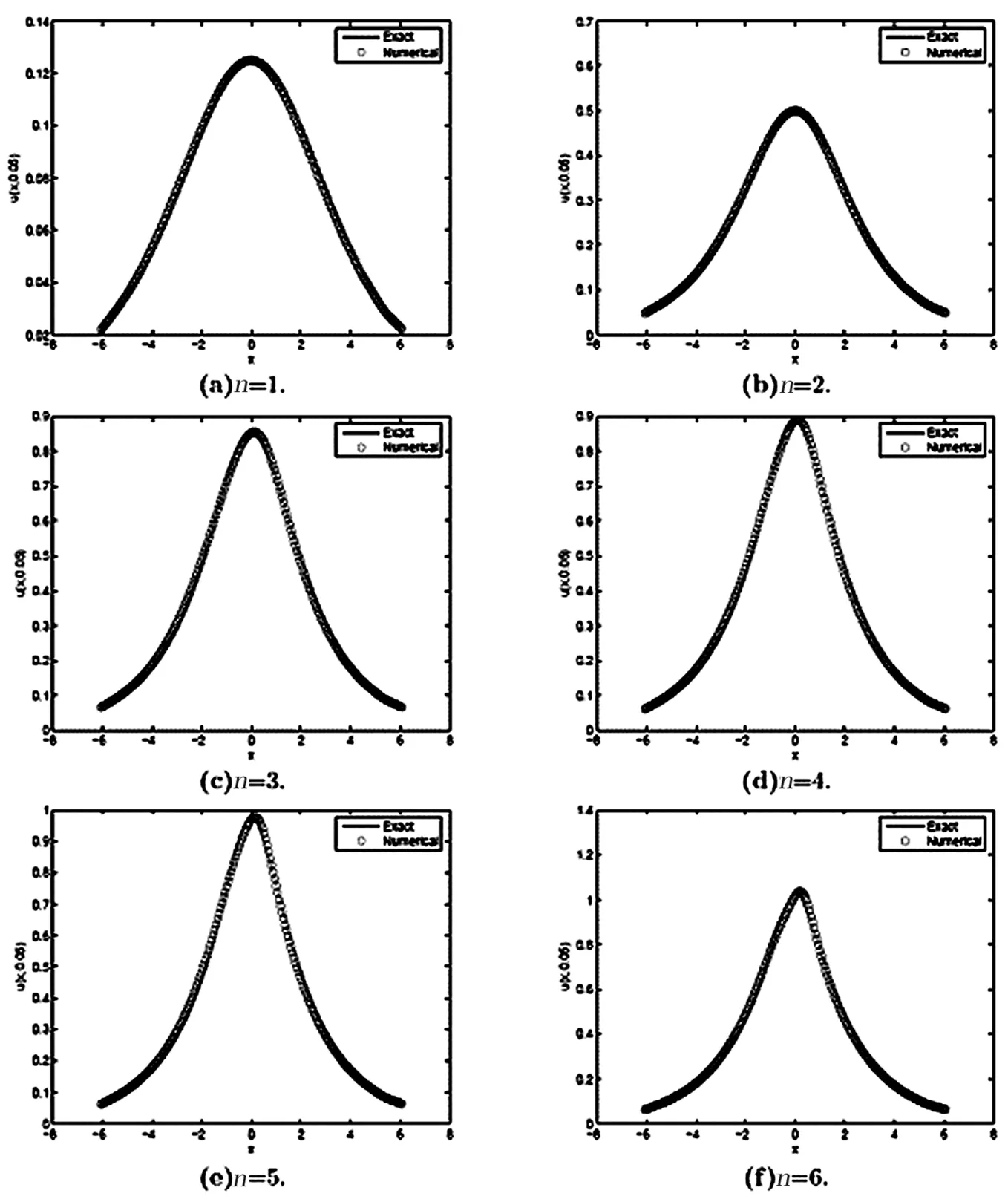
Fig.2:Comparison of exact and numercal solutions for different n at time 0.05 when c=0.25

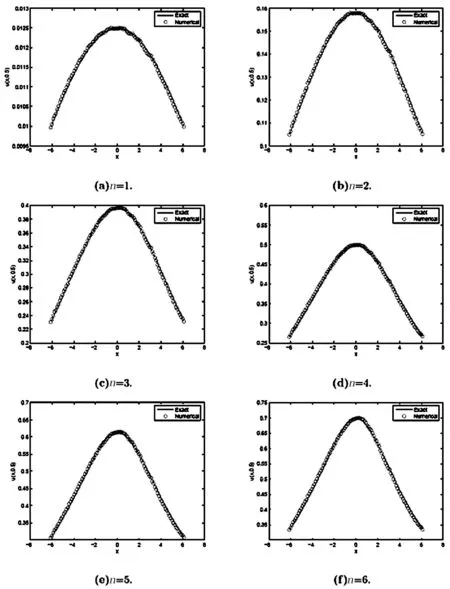
Fig.3:Comparison of exact and numercal solutions for different n at time 0.5 when c=0.025

Table1:AbsoluteerrorsfoundedbyusingEFDattimet=0.005

xn=4n=5n=6α=0.1-5.41.70662E-040.00280199060.00039146539.37512E-05-32.37651E-040.00400723420.00057642618.31771E-0502.51717E-060.00000432860.00000636628.44667E-0532.41954E-040.00040765190.00058587648.48665E-055.44.56803E-040.00073801450.00101496674.76929E-05

4 Conclusions

We constructed a new EFD scheme for simulating the traveling wave solutions of the GKdV equation. The numerical results show that our numerical method is efficient. The EFD method is very simple and easy to use. It is useful in seeking the approximate traveling wave solutions of other nonlinear evolution equations.

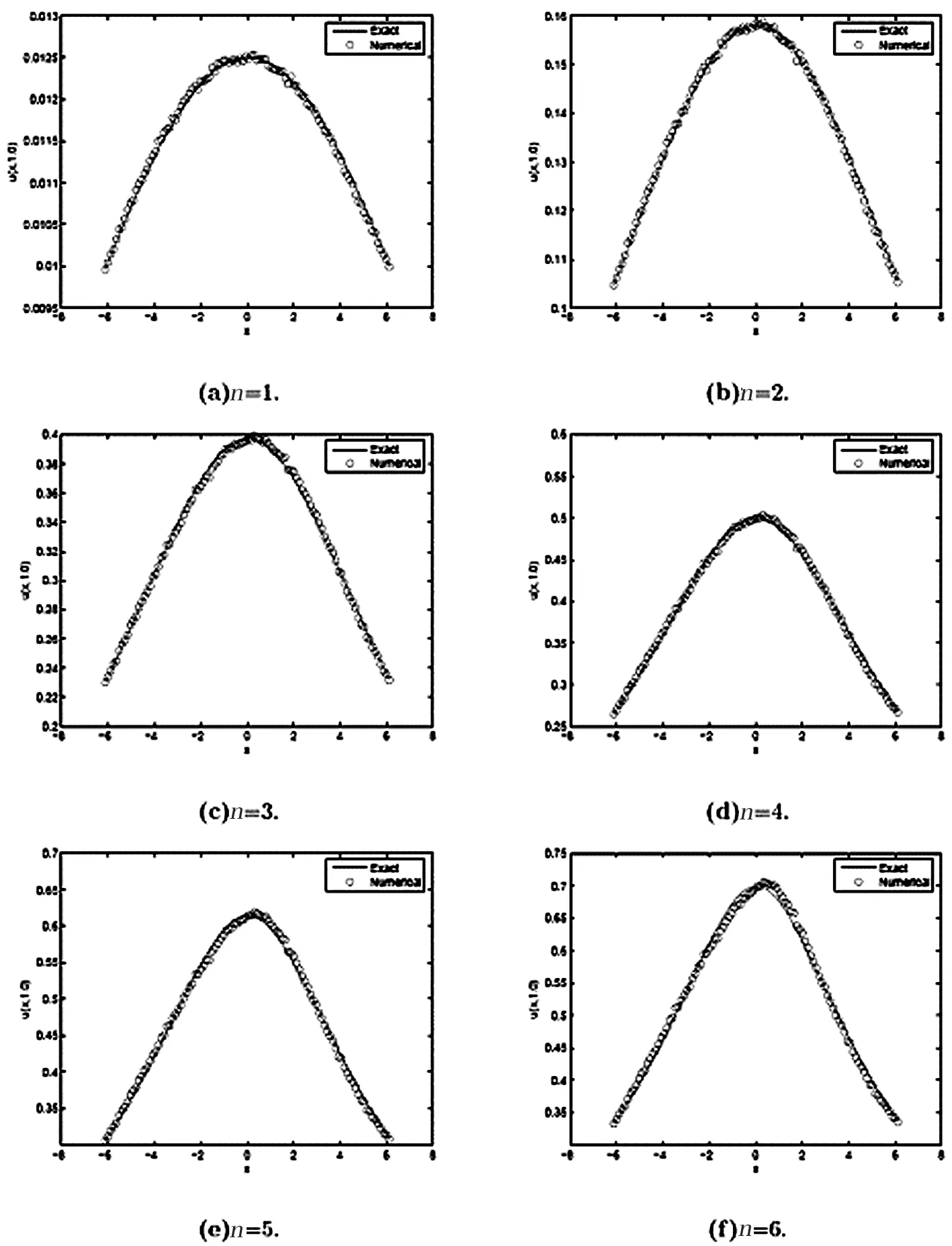
Fig.4:Comparison of exact and numercal solutions for different n at time 1.0 when c=0.025

〔参考文献〕

[1]Helal M A, Mehanna M S. A comparative study between two different methods for solving the general Korteweg-de Vries equation (GKdV) [J]. Chaos, Solitons & Fractals, 2007, 33: 725-739.

[2]Feng Z S, Knobel R. Traveling waves to a Burgers-Korteweg-de Vries-type equation with higher-order nonlinearities [J].J. Math. Anal. Appl., 2007, 328: 1435-1450.

[3]Zhang W G, Chang Q S, Jiang BG. Explicit exact solitary-wave solutions for compound KdV-type and compound KdV-Burgers-type equations with nonlinear term of any order [J]. Chaos, Solitons & Fractals, 2002, 13: 311-319.

[4]Feng Z. Traveling solitary wave solutions to evolution equations with nonlinear terms of any order [J]. Chaos, Solitons & Fractals, 2003, 17: 861-868.

[5]Li B, Chen Y, Qing Z H. Explicit exact solutions for new general two-dimensional KdV-type and two-dimensionalKdV-Burgers-type equations with nonlinear term of any order [J].J. Phys. A, 2002, 35: 8253-8265.

[6]Parkes E J, Duffy B R. An automated tanh-fucntion method for finding solitary wave solutions to nonlinear evolution equations [J]. Comput. Phys. Comm., 1996, 98: 288-300.

[7]Parkes E J, Duffy B R. Traveling solitary wave solutions to a compound KdV-Burgers equation [J]. Phys. Lett. A, 1997, 229: 217-220.

[8]Wang M L. Exact solutions for a compound KdV-Burgers equation [J]. Phys. Lett. A, 1996, 213: 279-287.

[9]Feng Z. On explicit exact solutions to the compound Burgers-Korteweg-de Vries equation [J]. Phys. Lett. A, 2002, 293: 57-66.

[10]Khater A H, ElKalaawy O H, Helal M A. Two new classes of exact solutions for the KdV equation via Backlund transformations [J]. Chaos, Solitons & Fractals, 1997, 8: 1901-1909.

[11]Helal M A. Chebyshev spectral method for solving KdV equation with hydro dynamical application [J]. Chaos, Solitons & Fractals, 2001, 12: 943-950.

[12]Helal M A. Soliton solution of some nonlinear partial differential equations and its applications in fluid mechanics [J]. Chaos, Solitons & Fractals, 2002, 13: 1917-1929.

[13]Bahadir A R. Exponential finite-difference method applied to Korteweg-de Vries equation for small times [J]. Appl. Math. Comput., 2005, 160: 675-682.