近共沸制冷剂R290/R134a PVTx性质的实验研究

杨 喜 祁影霞 陈 伟 张 华

(上海理工大学 上海 200093)

由于CFCs对臭氧层的破坏作用，国际上已经禁止生产和使用。现在所使用的替代制冷剂如R410A、R134a和R407C等虽然对臭氧层无害，但是由于其具有较高的GWP，对全球变暖依旧起着作用。

R290是一种天然的制冷剂，其 ODP值为零，GWP值小于12，符合当前对制冷剂环境性能的要求。此外，R290的基本物理性质与R22很接近，而且能与矿物油很好的互溶。目前，R290已经应用到冰箱、热水器等方面。但是，由于其具有较强的可燃性和爆炸性，最大充注量不高，只能用于制冷量较小的设备，应用范围受到限制［1－2］。

R134a的沸点为 －26.26℃，凝固点为 －96.6℃，不燃烧，不爆炸。以R134a作为阻燃剂，可以有效的减少可燃工质的燃烧范围或者完全抑制其燃烧。文献［3］的研究表明，当混合工质中R134a的体积分数超过13.87%，即质量分数超过27.1%时，任何浓度下混合工质都是不会发生燃烧爆炸的。当R134a的质量在55% ～65%之间时，R134a/R290混合物是近共沸混合物，它可以作为R22的替代制冷剂，具有优秀的循环性能［4］。目前国际上没有公开发表的R290/R134a混合工质的气相PVTx性质的文献报告，这里将用Burnett法测定三种质量配比的R290/R134a高精度PVT数据，并拟合状态方程。

1 实验装置

1.1 PVTx测试装置

制冷工质PVTx性质测试系统主要由恒温槽、压力测量系统、PVTx测试装置及自动化测试分析软件、真空系统、ASL F600温度测量系统组成。图1为制冷工质PVTx性质测试系统连接简图。

实验装置是以Burnett法为基础，用于高精度工质PVTx性质的测试。Burnett法是1936年由美国工程师Burnett S．E提出的的一种PVT性质测定方法，随后又有许多研究人员对其具体测量和数据处理的方法进行了深入研究［5－7］，目前该方法已经非常成熟。它最大的优点是避免了测量容积的体积标定和装置中气体质量的测量。通过等温膨胀的方法，测量一系列气体的压缩因子，然后利用气体压缩因子的定义计算获得相应的气体密度值。

图1制冷剂PVTx性质测试系统图Fig．1 The measurement systerm diagram of refrigerants PVTx properties

如图2所示，实验本体是由两个高压容器构成，一个作为主容器VA，其内容积为728 mL，另一个作为膨胀容积VB，其内容积为241 mL，两个容器间通过管道阀门连接。通过主容器向膨胀容器的膨胀放气即可以实现工质压缩因子的测量。

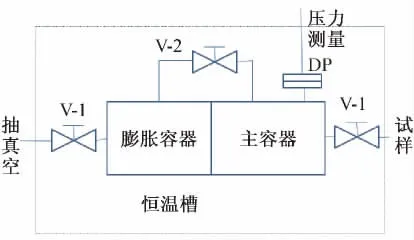
图2 Burnett法测量气相PVT性质原理图Fig．2 The schematic diagram of the gas PVT properties measurement with Burnett method

1.2 自动化测试分析软件

应用的自动化测试分析软件包括PVTx测试软件和数据分析软件。PVT测试软件可用于对恒温槽温度的控制，测量实验装置中样品的温度、压力，最后可以拟合测量点下相应的密度值;PVT数据分析软件可以用于分析拟合工质的气体状态方程。

1.3 实验原理

根据热力学基本知识，气体的压缩因子Z的定义式为:

式中:p为气体压力;T为气体温度;V是气体容积;n为气体摩尔质量;R为理想气体常数。

如果向实验装置中的主容器VA(抽过真空)中充入一定质量n0的待测工质气体，则待测工质的气体压缩因子Z0为:

式中:p0和T分别为待测工质的压力和温度，通过实验测量获得。

当主容器VA中的温度压力稳定后，打开阀门V－2，气体将流向膨胀容器，等到温度和压力值稳定后，通过测定主容器的气体压力p1，得出气体在第一次膨胀后的气体压缩因子值Z1:

关闭膨胀阀门V－2，对膨胀容器和相关管路进行抽真空，然后关闭阀门V－1。等主容器中气体的压力和温度值稳定后，打开膨胀阀门V－2进行第二次膨胀，并测量稳定后的压力p2，同理我们可以得到第二次膨胀后的气体压缩因子Z2。重复上述过程，直至膨胀压力足够低。这样就可以得到一条在温度T下的等温膨胀线。

根据膨胀过程的特点，第r次膨胀前后容器内的工质量是相同的，则我们可以得到:

由此得到Burnett法压缩因子的递推关系式:

通过定义容积常数Nr:

式(5)可以写成:

对于一套实验装置，Nr的值变化很小。因此，可以认为其为常数，简化为N。得到下式:

多次重复上面的式子，我们可以得到 Zr和Z0的关系式:

由上式可知:在测定pr后，我们想确定地r次的膨胀气体的压缩因子，还得确定两个常数，N和Z0/p0，一般把Z0/p0记为A，并且成为充气常数。

对于容积常数N的确定，我们由(8)可以得出:

我们知道如果气体为理想气体，即为压力趋近于零时，则气体的压缩因子为1，于是可得:

可以看出，N值可以通过等温线上的一系列压比值外插到压力零点得到。从N值的定义式我们知道，其与测量工质的种类无关。大量研究表明:氦气、氢气、氮气对上述关系式有很好的线性关系，而且线性关系可以保证有需要的压力。因此，在实际工质的PVT测量实验中，大多是选择上述三种气体进行N值标定。

一定温度下，对于待测气体的统一系列Burnett法实验，A为定值。

把维里方程中Berlin展开式Z=1+Bp+Cp2带入上式整理得到:

拟合得到的b0即为1/A，则充气常数为:

再利用上面的方法得到容器的N和A值后，就可以计算得到每次等温膨胀后的气体压缩因子Zr值了，然后利用气体压缩因子的定义式可以得到每次膨胀后气体的密度值:

2 实验步骤

实验对R134a/R290的质量分数分别为50%/50%、55%/45%和60%/40%的三种配比进行测量，实验测试步骤:

1)利用配气系统按要求的质量比配取实验所需的混合工质。

2)打开充气阀Φ1，给实验装置主容器中充入混合工质，一般要保证待测工质处于饱和状态或近饱和状态，可以根据主容器的体积计算出该温度下达到饱和态所需要充入工质的大概质量。关闭阀门Φ1，将待测气体容器与压力采集系统连接。

3)利用PVT测试软件设定恒温槽温度，待温度波动小于±10 mK/15 min时采集温度。

4)压力测量:等压力值稳定选取一段压力值，得到 T0，p0，打开Φ2，等待膨胀容器与主容器平衡，当温度波动在10 mK/5 min以内、压力波动为±0.01%以内时关闭Φ2，测量一段压力值，得到 T0，p1。打开Φ3及 Φ4，进行排样、卸压。关闭 Φ4，打开 Φ5抽真空，抽到10 Pa以下，等待半个小时到一个小时。关闭Φ3及 Φ5，打开 Φ2阀门，等待膨胀容器与主容器平衡。当温度波动在10 mK/5 min以内、压力波动为±0.01%以内时关闭Φ2，测量一段压力值，得到 T0，p2，依次往下进行…T0，pn，直到压力在100 kPa左右，停止实验。

5)选取另一温度点T1，重复第3步，直至温度所需温度Tn。

此外，Burnett法测定工质的PVTx性质最关键的是容积常数N的标定和充气常数的确定。在测量混合工质的PVTx性质前，采用纯度为99.999%的氮气对实验系统进行了N值标定，标定实验的操作步骤同前面介绍的实验步骤相同，具体的实验数据见下表1。

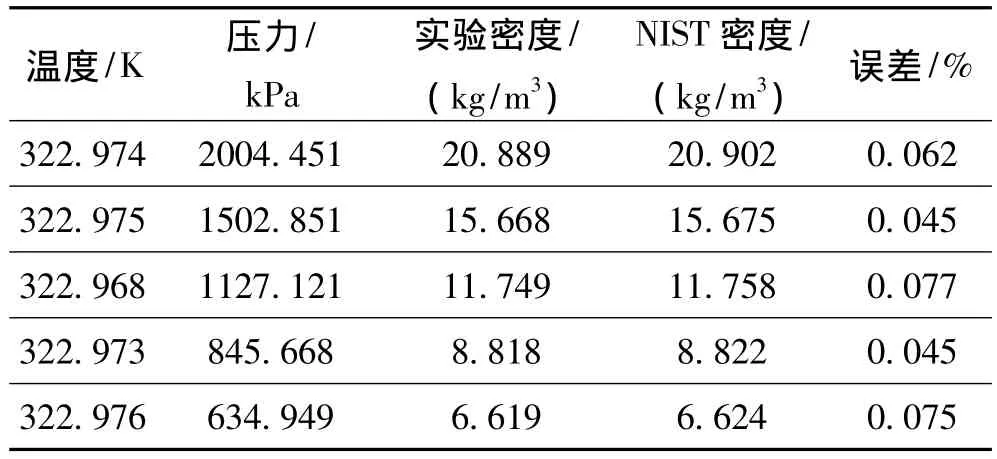
表1 N值标定实验数据Tab．1 The experiment data of N calibration

根据前文介绍的容积常数N值的标定办法和最小二乘法，取压力值为加权因子，本文得到了322.97 K的容积常数N值为1.332045。

3 实验结果及分析

对温度252～320 K区域范围内三种不同质量配比的混合工质的气相PVTx性质进行了测量，为了能够比较清楚的了解三种质量配比R290/R134a的气相PVTx性质的实验数据分布状况，图3，图4，图5为三种配比混合工质的所有实验数据在p-T图上的分布，其中各图所示曲线为其饱和蒸汽压力曲线。表2给出了R290/R134a质量配比为50%:50%时的实验饱和蒸汽压数据与refprop8.0数据的比较。从表2可以看出，实验饱和压力与refprop数据的最大误差为1.17%，最小误差0.01%，平均误差为0.74%，精度很高。其中，误差很大一部分是由配气过程中混入了少量空气等杂质引起的，如果采取更精密的配气系统，可进一步提高其测量精度。

表2 R290/R134实验饱和蒸汽压与Refprop8.0数据的比较(R290/R134a质量配比50%:50%)Tab．2 The comparison of saturated vapor pressures of R290/R134a between experiments and Refprop 8.0 data

图3混合工质A的PVT实验数据在p-T图上的分布(R290/R134a质量配比50%:50%)Fig．3 The PVT experimental data in the p-T chart distribution of mixed refrigerant A

图4混合工质B的PVT性质实验数据在p-T图上的分布(R290/R134a质量配比45%:55%)Fig．4 The PVT experimental data in the p-T chart distribution of mixed refrigerant B

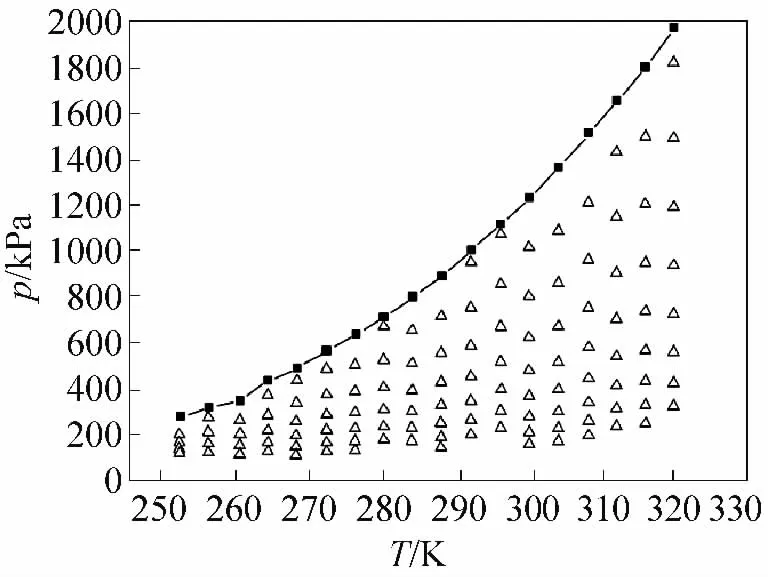
图5混合工质C的PVT性质实验数据在p-T图上的分布(R290/R134a质量配比40%:60%)Fig．5 The PVT experimental data in the p-T chart distribution of mixed refrigerant C

利用混合工质的第二，第三维里系数方程，分别得到三种混合工质气相维里状态方程:方程如下式(16):

把混合工质的第二、第三维里系数拟合成如下所示方程形式:

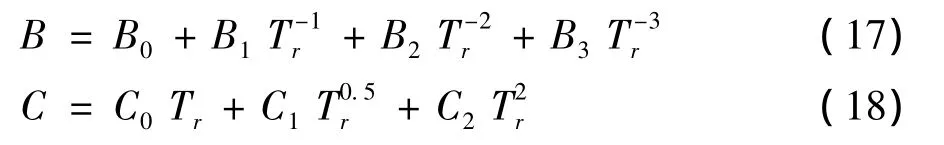
上式中:

Tc为工质的临界温度。多元混合工质的临界温度Tcm一般而言有以下两种比较简便的计算方法:

上式中Tci为混合工质中各纯组分的临界温度，xi为各纯组分的摩尔分数，我们取式(5)和(6)的平均值作为混合工质临界温度的计算值:

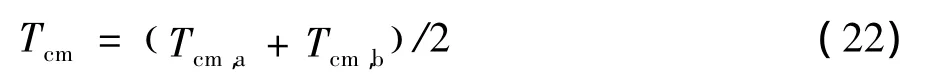
由式(7)计算得到混合工质A，B，C的临界温度分别为 Tcm，A=371.19 K，Tcm，B=371.38 K，Tcm，C=371.58 K。上面气体方程中，温度、压力和密度的单位分别为:K，MPa，mol/cm3，R为普适气体常数。三种工质的维里方程各参数分别见表3～表5。

表3混合工质A维里方程各参数的值Tab．3 The parameters’values of virial equation of mixed refrigerants A

表4混合工质B维里方程各参数的值Tab．4 The parameters’values of virial equation of mixed refrigerants B

表5混合工质C维里方程各参数的值Tab．5 The parameters’values of virial equation of mixed refrigerants C

为了比较实验所得第二，第三维里系数与上述方程(17)，(18)的吻合情况，同时为了了解混合工质的第二，第三维里系数与温度存在的关系，图6～图11分别给出了三种混合工质第二，第三维里系数与温度的关系图，图中的曲线即为方程，可以看出实验数据与方程的吻合状况良好。第二维里系数B随着温度的升高而增大，第三维里系数随着温度的升高而降低。维里系数不仅是温度T的函数，还与气体本身特性有关。当压力p→0，体积V→∞ 时，维里方程还原为理想气体状态方程。统计力学指出，第二维里系数反应了两个气体分子间的相互作用对气体PVT关系的影响，第三维里系数则反应了三分子相互作用引起的偏差。

理论上来说，新方程可以外推至临界温度Tc和三相点温度Ttr，所取温度范围越大、温度点越多，方程的精度就越高。但是由于接近相变区域，精度会不断下降，因此，不适用于相变点附近区域。

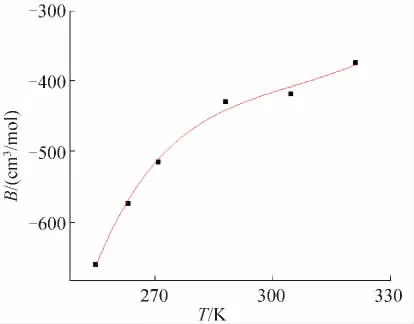
图6混合工质A第二维里系数B与温度关系Fig．6 The relationship between the second virial coefficient B and the temperature of mixed refrigerants A

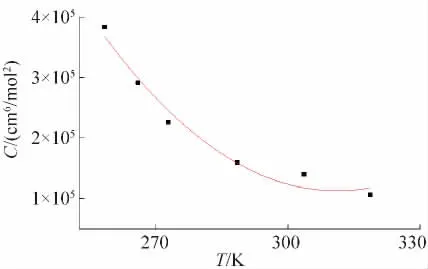
图7混合工质A第三维里系数C与温度关系Fig．7 The relationship between the third virial coefficient C and－200 The temperature of mixed refrigerants A

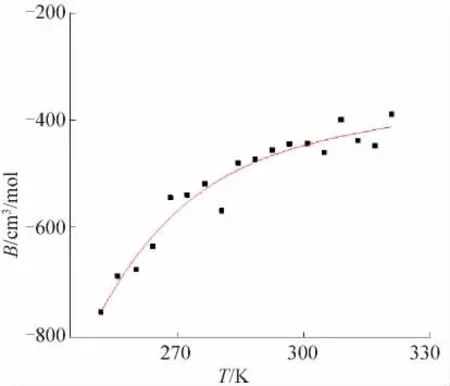
图8混合工质B第二维里系数B与温度关系Fig．8 The relationship between the second virial coefficient B and the temperature of mixed refrigerants B

4 结论

通过高精度的PVTx实验系统，以Burnett等温膨胀法研究了近共沸制冷剂R290/R134a三种配比的热力学性质。根据实验结果拟合出相应的气体状态方程。实验结果与方程的平均误差仅为1%左右，具有较高的精度，为目前正在进行的制冷工质替代研究提供了重要的参考。

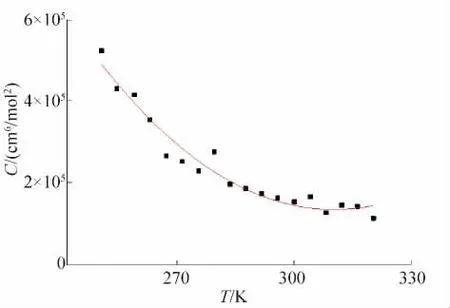
图9混合工质B第三维里系数C与温度的关系Fig．9 The relationship between the third virial coefficient C and the temperature of mixed refrigerants B

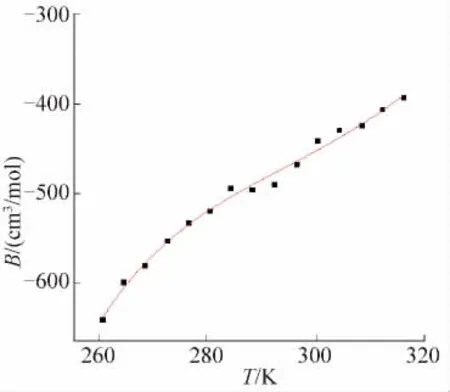
图10混合工质C第二维里系数B与温度的关系Fig．10 The relationship between the second virial coefficient B and the temperature of mixed refrigerants C

图11混合工质C第三维里系数C与温度的关系Fig．11 The relationship between the third virial coefficient C and the temperature of mixed refrigerants C

本文受上海市重点学科建设项目(S30503)，上海市教育委员会科研创新项目(11YZ119)，上海市优秀学科带头人计划项目(10XD1403100)资助。(The project was supported by Shanghai Leading Academic Discipline Project(No．S30503)，Innovation Program of Shanghai Municipal Education Commission(No．11YZ119)，Excellent Academic Leaders Project of Shanghai(No．10XD1403100)．)

［1］陈光明，高赞军，韩晓红．HCFC-22替代制冷剂研究进展及其相关问题讨论［J］．制冷与空调，2011，11(1):101-109．(Cheng Guangming，Gao Zanjun，Han Xiaohong．The research progress and discussion of alternative refrigerants to HCFC-22 and related issues［J］．Refrigeration and Air-condition，2011，11(1):101-109．)

［2］朱明善，史琳．在家用/商用空调中用R32替代R22的探索［J］．制冷与空调，2009，9(6):31-34．(Zhu Mingshan，Shi Lin．Re-analysis on Using R32 to Substitute for R22 in Househould/commercial Air-condition［J］．Refrigeration and Air-condition，2009，9(6):31-34．)

［3］田贯三，马一太，杨昭，等．可燃制冷剂爆炸极限及抑制的理论与实验研究［J］．山东建筑工程学报，2001，16(2):58-63．(Tian Guansan，Ma Yitai，Yang Zhao，et al．The theoretical and experimental research of flammable refrigerant explosion limit and inhibition［J］．Journal of ShanDong institute of ARCH and ENG，2001，16(2):58-63．)

［4］徐明仿，杜维明，晏刚．近共沸制冷剂R134a/R290的研究［J］．制冷与空调，2004，4(5):71-74．(Xu Mingfang，Du Weiming，Yan Gang．Study of the near-azeotropic mixture of R134a and R290［J］．Refrigeration and Air-condition，2004，4(5):71-74．)

［5］Silberberg I H，Kobe K A，McKetta J J．Gas compressibility with the Burnett Apparatus methods and apparatus［J］．Journal of Chemical and Engineering Data，1959，4(4):314-323．

［6］Kramer G M，Miller J G．Compressibility of gases III．The second and third virial coefficients of mixtures of helium and nitrogen at 30 ［J］．Journal of Physical Chemistry，1957，61(6):785-788．

［7］Wielopolski P，Warowny W．A fast least-squares method for reduction of Burnett data to compressibility factors and virial coefficients［J］．Physica A，1978，91(1/2):66-72．