新型乡村社区中心村空间最优布局研究
2014-08-02崔许锋蒋月华
崔许锋,蒋月华
(1.中南财经政法大学 工商管理学院,武汉 430073;2.湖南师范大学 资源与环境科学学院,长沙 410081)
新型乡村社区中心村空间最优布局研究
崔许锋1,蒋月华2
(1.中南财经政法大学 工商管理学院,武汉 430073;2.湖南师范大学 资源与环境科学学院,长沙 410081)
构建新型乡村社区、实现农村发展是中国城镇化的重要路径之一。构建空间最优布局模型,可为中心村空间布局选择提供方法支撑,实现中心村空间选址的最优化。可根据中心村基本内涵建立科学的中心村空间最优布局 综合评价体 系,基于综 合评价方法 和 Dijkstra算法,构建居民点 综合评价模 型和最短 路 径 模 型 。 以 鄂 西 南 M镇为例,以调研数据为依据,采用居民点综合评价模型和最短路径模型对居民点进行计量分析,可得出各评价单元中心村综合评价指数,通过比较评价指数从而筛选出最优的中心村布局,实现中心村的科学选址。研究结果表明居民点综合评价模型和最短路径模型的在中心村空间最优布局的选择上具有有效性。中心村居民点综合评价模型是中心村内涵的数量化表达,以图论法寻求最优空间区位,提高了中心村选址决策的科学性,对于城镇化进程的中心村科学建设具有重要的意义。
乡村社 区;中心村 ;居民点建 设;Dijkstra算 法;综 合评 价模型 ;空 间布局
改革开放三十多年来,中国城镇化发展迅速,城镇化率已经由 1978年的 17.91%提高到 2012年的52.6% (陆 大 道,2013)[1],并预计 到 2020年,中 国城市化率将达 60%。相关研究表明,城镇化率达到30%—70%,城镇化将进入快速发展阶段 (Ray M N,Northam L,1979)[2]。 当 前 中国 正 处 于 快 速 的 城镇化进程中,城镇化问题成为中国发展的重要问题之一。城镇化是在一定的阶段构建现代城市体系,改善经济社会活动,改革土地利用方式的进程,是社会、经济 和 政 治 发 展 的 积 极 结 果 (Rimal,2011)[3],在农业社会向工业社会、乡村文明向现代文明的转变,在城镇化过程中,如何改变农村落后的面貌、推进农村向现代乡村社区的转变成为研究的重要课题,中心村的规划与建设无疑是实现现代乡村社区的重要路径之一。
中心村是基于农村经济、社会、人口等因素的发展,在一定的区域范围内以原居民点或者新选居民点为中心,由若干村落组成,形成区位条件较好、人口较为集中、经济发展条件相对优越、基础设施配套齐全及公用服务相对完善,对周边一定范围内经济发展起到带动和辐射作用的新型农村社区(徐全勇,2005)[4]。在 其 内 涵 上,首 先,中 心 村 是 由 若 干村落构成,在空间上处于辐射和带动作用,是当前新型农村社区建设的主要选择 (王福定,马骁,2006)[5]。其次,中 心 村 是 城 乡 居 民 点 布 局 的 一 种形式,是能支撑最基本生活服务等基础设施和公用设施要求的最小规模的居民点,其介于乡镇和行政村之间,是农村居民点最基层的完整的规划单元。再次,中心村是城乡体系的基本单元,是“中心村—乡镇—城市”体系的重要构成(刘彦随,2011)[6]。
中心村的建设是促进农村发展的重要选择,将有力推动农村经济社会进步,对实现城乡统筹发展、缩小城乡差距具有重要意义。首先,中心村是新农村建设的重要要求。在目前全面建设小康社会的背景下,国家提出要按照新农村建设 20字方针要求,其中“乡风文明”、“村容整洁”是新农村建设方针的重要内容。但是目前农村居民点的分散布局现状阻碍了新农村建设的实施,因为只有当农村居民点集聚到一定程度,才能够进行基础设施和公用设施建设而不造成资源的浪费,使农村居民享受到城镇居民同等 的 基 础 设 施 和 医 疗 科 学 教 育 文 化 服 务[7]。中心村建设实现了农村居民点的空间集聚,实现了农村基础设施和公用设施建设成本的边际递减。其次是实现“中国梦”的要求。“中国梦”是 2012年习总书记和新一届中央领导集体在国家博物馆参观《复兴之路》展览过程中提出的。“中国梦”具体在农村发展过程中,就体现在让农民享受国家发展的成果,实现城乡的共同发展。第三,中心村建设是实现土地集约利用的重要模式。当前农村建设用地的利用十分粗放,而且在城市化过程中农民迁移流动频繁,许多农民定居城市,其原住宅处于闲置状态,这也造成了极大的浪费,所以农村建设用地还有较大的潜力可以释放。通过中心村建设,可以提高农村建设用地的集约利用度(欧阳安蛟,蔡锋铭,陈立定,2009)[8],同时废弃的原农村居民点可以采用整理复垦的方法恢复为农用地,从事农业生产活动,防止了土地浪费。鉴于以上的认识,在中国城镇化发展过程中,新型乡村社区中心村建设意义重大,如何实现中心村空间的最优布局择优成为重要的研究课题。
一、研究进展评述
目前对于中心村规划与建设的研究已有不少的文献,研究多集中在空间最优布局、规模设计、融资管理、政策与制度安排等方面,这为研究提供了较为丰富的文献资料。在中心村空间最优布局研究方面,已经有不少有益的研究和探索。有研究在调研上海市“迁村并点”政策的基础上,认为中心村建设应该遵循一般村落向交通便利的村落集中、经济落后村落向经济发达村落集中、小规模村落向大规模村落集中的原则(任春洋,姚威,2000)[9];有研究认为中心村应该形成一定的合理规模,有利于基础设施建设和公用设施的配套,方便生产和生活,所以空间最优布局选择应该遵循区位优势、联系功能、规模经济、集约用 地 的 原则 (王 士兰,陈 前 虎,2001)[10];也有研究认为,中心村建设以实现农业产业化经营,推动城镇化为目的,中心村选址应遵循区位优势、联系合理(经济、交通、社会、历史等联系)、规模经济、节约用地的原 则 (张 京 祥,张小 林,张 伟,2002)[11];还有研究以中心村建设的中心地理论、城镇服务业的规模经济理论以及村域空间结构演变理论为基本理论,在分析了中国发达地区中心村建设的可操作性的基础上,提出了中心村选址的交通不便的村向交通便利的村集中、经济落后的村向经济发展领先的村集中、集镇附近的村向镇区集中、符合城镇体系规划等基本 原 则 (徐 全勇,2005)[12]。在 方 法 方 面,有研究采用构建综合评价方案,对村落进行综合评价,并对评价结果采取聚类分析的方法进行处理,形成 I、II、III、IV几种类别,以筛选最优类别进行中心村建设(谢晓鸣,2007)[13]。还有研究将 GIS技术用于中心村择优。以巩义市西村镇为研究区域,采用AHP法建立综合评价体系,通过 GIS空间分析得到各村评价参数,最后运用多因素综合分析计算村庄潜力评价综合分值,选出最优村落布局(张艳粉、刘科问、陈伟强,2013)[14]。
上述这些研究有助于加深对中心村空间最优布局的原则、方法的认识,拓展了对中心村空间最优布局研究的深度,为本文的研究提供了有益的参考和借鉴。但是,综合以上关于中心村空间最优布局的研究,可以看到目前研究多重理论而缺乏实践,一般从规范性角度去探讨中心村空间最优布局的原则,而缺乏对中心村空间最优布局实证角度的研究,定量研究工具利用不足,这无疑存在进一步研究的必要。本文的研究将从中心村基本内涵切入,根据中心村基本内涵建立科学的中心村空间最优布局综合评价体系,构建综合评价模型和最短路径模型,对居民点进行计量分析,从数量角度,寻求中心村空间最优位置。
二、空间最优布局模型构建
1.居民点综合评价模型
根据中心村的一般定义,可以知道中心村是区位因素、社会因素、经济因素的综合体,那么设 CI为中心村综合评价指数,于是中心村综合评价指数是以区位因素、社会因素、经济因素为自变量的函数,所以中心村指数模型可以用方程 I表示。
方程 I:CI=f(LOC,SOC,ECOF)
其中,CI表示中心村综合评价指数,LOC表示区位因素,SOC表示社会因素,ECOF表示经济因素。社会因素和经济因素是宏观因素,需要用具体的指标表示,那么根据中心村的定义,结合新农村建设用对中心村的具体要求,可以将中心村内涵归结为六个方面:区位优势;人口相对集中;具有一定的非农产业支撑,提供农民就业并具有人口集聚力;经济发展相对优越;基础设施配套齐全;公用服务相对完善。根据这五个方面的内涵选择区位因素(LOC)、人口规模(POP)、非农产业规模(NAI)、经济发 展 水 平 (ECO)、基 础 设 施 (INF)、公 共 服 务(PUBS)这五个评价指标为中心村评价指标,那么方程 I可以转化为方程 II。
方 程 II:CI=f(LOC,POP,NAI,ECO,INF,PUBS)
或者可以写成:
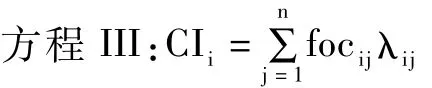
其中 CIi为第 i个村落的中心村综合评价指数,focij为 第 i个 村 落 j个 要 素 的 评 价 指 标 的 评 价 值 ,λij为第 i个村落 j个要素的权重。
中心村最优位置的选择是一个最优化问题,对CIi求最大值,最大值对应的村落即为中心村的最优布局,于是得出方程 IV。
方程 IV:KEYV=MAX(CIi)
2.最短路径模型
采用 Dijkstra算 法 对 区 位 进 行 计 算,迪 杰 斯 特拉(Dijkstra)算 法,其 基 本 思 想 是 按 距 u0从 近 到 远为顺序,依次求得 u0到各顶点的最短路和距离,直至 v0(或直至 G的所有顶点),算法结束。为避免重复并保留每一步的计算信息,采用了标号算法。下面是该算法的基本原理。
(i)令 l(u0)=0,对 v≠ u0,令 l(v)=∞,S0={u0},i=0。

(iii)若 i=|V|-1,停止;若 i<|V|-1,用 i+1代替 i,转(ii)。
算法结束时,从 u0到各顶点 v的距离由 v的最后一次的标号 l(v)给出。在 v进入 Si之前的标号 l(v)叫 T标号,v进入 Si时的标号 l(v)叫 P标号。算法就是不断修改各项点的 T标号,直至获得 P标号。若在算法运行过程中,将每一顶点获得 P标号所由来的边在图上标明,则算法结束时,至各项点的最短路也在图上标示出来了(罗先会,2006)[15]。
三、空间最优布局模型的应用
研究以湖北省西南部 M镇为研究区域,采用居民点综合评价模型 和 基 于 Dijkstra算法 的 最 短 路 径模型,对该镇东部 7个村庄的中心村影响因素进行评价,得出最优化的中心村布局。
1.研究区概况
M镇(见图1)位于湖北省西南部,辖区下辖 11个村及一个林场。出于耕地资源保护的目的,中心村建设不采用新选址的方法,避免对农用地占用,而是采用区位、经济、社会等较优越位置的已有村落,利用原有农村建设用地开展中心村建设,这样可以提高土地利用效率,符合国家耕地保护的基本国策。研究拟在 M镇东部 7个村中,选择某一原有村落,以此为中心开展中心村建设。选址的原则是具有中心地区位优势、人口相对集聚、对其他村落有一定辐射力、经济发展相对发展较好、基础设施及公用设施相对其他农村居民点具有优越性。

图1 M镇空间布局图
2.区位条件指标计算
Dijkstra算法一种典型的最短路径计算方法,是数据结构、图论、运筹学等领域的基本算法之一。Dijkstra算法用于 计 算 一 个 节 点 到 其 他 所 有 节 点 的最短路径,主要原理是以起点为中心层层扩展,直到终点为止[16]。研究中 心 村 最 优 选 址 选 用 此 算 法 的原因是由于农村居民点之间的最短距离不是直线距离,而是二者之间路径长度集合的最小值。比如 A、B两个农村居民点,它们之间的联结可能有多种方案,存在多条没有直接的路径联结,而通过第三农村居民点的联系,通过第三农村居民点的中转才能实现了两个居民点的联系,也就是说 A、B两个居民点直接的联结路径可能存在多条,要加以不断的比较,然后 才 能 选 出 最 短 的 路 径。 通 过 Dijkstra算 法、利用计算机的迭代技术,可以很方便地找到农村居民点与剩余农村居民点之间的最短路径。
根据图1,由图论知识可以得出,图1为简单图,因为其既没有环也没有重边,于是可以将图1抽象为图2。G=(V,E,ψ),其中,V为顶点集,V={v1,v2,…,vn},E为边集,E={e1,e2,…,en},ψ为关联函数,在此表示为路径的长度。图 G如图2所示。

图2 无向图 G
根据图2所示,计算的路径长度,得到 M镇东部七个农村居民点的邻接矩阵见表1。

表1 M镇东部七个农村居民点的邻接矩阵
根据 图 的 邻 接 矩 阵,采 用 Dijkstra算 法 计 算 出最短路径矩阵见表2。

表2 M镇东部七个农村居民点最短路径矩阵

表3 Vi的区位指数
3.中心村综合评价
根据方程 II选用的综合评价指标,选择中心村指数为目标层,区位优势与社会经济发展指标为因素评价层,社会经济发展指标又划分为人口规模(POP)、非 农 产 业 规 模 (NAI)、经 济 发 展 水 平(ECO)、基础设施(INF)、公共服务(PUBS)五个评价指标。区位条件的 数 据来 源 于 Dijkstra算 法 模 型的计算结果,农村居民点发展数据来源于调研访谈。鉴于区位优势与农村居民点发展同等重要,权重各取 0.5。在社会经济发展内部人口规模(POP)、非农产业规模(NAI)、经济发展水平(ECO)、基础设施(INF)、公共服务(PUBS)同等重要,各取 0.1。将各指标标准化后可得,标准化矩阵见表4。

表4 中心村综合评价指标标准化矩阵
最后得出的各个村庄的得分为表5,根据表5中各个农村居民点的得分,可以看出 V4,得分最高,V6次之,V1得分最低。故而选择 V4,V6可以作为备选方案,而 V1、V2得分较低,在中心村选址中须避免选址此两处位置。

表5 Vi中心村综合评价结果
四、结论与讨论
采用居民点综合评价模型和最短路径模型对中心村位置最优化问题进行了定量分析,根据定量分析的结果,实现了对乡村社区中心村位置最优布局,表明了居民点综合评价模型和最短路径模型在中心村最优布局方面的有效性,为中心村空间位置的选择提供了新的思路。居民点综合评价模型和最短路径模型在中心村空间最优布局研究中主要有以下优势:
首先,居民点综合评价模型全面涵盖了中心村的内涵,是中心村内涵的数量化。居民点综合评价模型的正确设定决定了评价结果的可信度,是中心村空间区位选择从定性研究转化到定量研究的纽带。该评价模型从中心村区位优势、人口相对集中、具有一定的非农产业支撑、经济发展相对优越、基础设施配套齐全、公用服务相对完善六个内涵出发,将抽象的概念具体化,实现了对居民点的综合评价,并对比分析评价结果实现中心空间位置的最优选择。
其次,利 用 Dijkstra算 法 并 结 合 计 算 机 技 术 可以方便地 实 现 最 优 区 位 条 件 的 选 择。 Dijkstra算 法作为计算最短路径的优秀方法,将其引入到中心村区位条件评价中,可以方便析出居民点到其他居民点最短路径,再赋权重求和便可以方便得出最优的空间 区 位。研 究 基 于 图 论 理 论,采 用 Dijkstra算 法将图论知识应用于居民点位置选择,是图论理论在中心村空间布局选择中应用的有益尝试。
研究为中心村位置的最优化研究提供了新方法、新思路,由于空间异质性的存在,不同的区域需要根据实际情况进行修正。研究采用的评价体系是一般化、普遍化的评价体系,不同区域可以根据自身具体的情况进行调整。比如居民点综合评价模型中,对区位条件、经济因素、社会因素的评价指标及权重计算各地有不同的具体情况,可以根据具体的区域实际,选择适合区域自身发展的评价指标体系。指标权重的计算也需要根据实际情况选择和计算,方法有德尔菲法、层次分析法、因素成对比较法、熵权法等,根据情况取舍,或者多种方法加权求值。
总之,在中国城镇化发展过程中,新型乡村社区建设意义重大,没有城乡的共同发展就不能实现全社会的和谐和可持续发展。中心村的科学布局作为新型社区建设的重要环节,在乡村社区规划与建设中决定了乡村社区的发展空间和潜力。将经济学评价模型与空间最优理论引入到中心村空间位置评价中,为中心村的规划布局提供了新的研究工具,具有相当的应用价值和现实意义。
[1]陆大道.地理学关于城镇化领域的研究内容框架[J].地理科学,2013(8):897-901.
[2]Ray M N,Northam L.Urban Geography[M].New York:John W illey&Sons,1979.
[3]Rimal B.Urban Development and Land Use Change of Main Nepalese Cities[D].W roclaw:University of W roclaw(Unpublished),2011.
[4]徐全勇.中心村建设理论与我国中心村建设的探讨[J].农业现代化研究,2005(1):48-52.
[5]王福定,马骁.中心村规划建设实践中的问题与对策——以浙江省温岭市为例[J].城市规划,2006(7):48-51.
[6]刘彦随.科学推进中国农村土地整治战略[J].中国土地科学,2011(4):3-8.
[7]汪胜洋.城乡统筹的阶段特征与发展战略思路——以上海为例[J].江汉学术,2013(2):5-13.
[8]欧阳安蛟,蔡锋铭,陈立定.农村宅基地退出机制建立探讨[J].中国土地科学,2009,23(10):26-30.
[9]任春洋,姚威.关于“迁村并点”的政策分析[J].城市问题,2000(6):45-48.
[10]王士兰,陈前虎.浙江沿海地区中心村建设规划的思考——以温岭市为实例[J].城市规划,2001(8):62-64.
[11]张京祥,张小林,张伟.试论乡村聚落体系的规划组织[J].人文地理,2002(1):85-88.
[12]徐全勇.中心村建设理论与我国中心村建设的探讨[J].农业现代化研究,2005(1):48-52.
[13]谢晓鸣.论江汉平原地区中心村的建设与选择[D].武汉:华中农业大学,2007:35-44.
[14]张艳粉,刘科问,陈伟强.基于 AHP和 GIS的中心村建设选址研究——以巩义市西村镇为例[J].地域研究与开发,2013(3):149-153.
[15]罗先会.多波长光网络的路由算法和仿真的研究[D].南京:南京邮电大学,2006:27.
[16]于德新,杨薇,杨兆升.重大灾害条件下基于 GIS的最短路径改进算法[J].交通运输工程学报,2011(4):123-126.
责任编辑:刘洁岷
(E-mail:jiemin2005@126.com)
F299.22
A
1006-6152(2014)06-0105-05
2014-05-09
本 刊 网 址·在 线 期 刊 :http://qks.jhun.edu.cn/jhxs
国家自然科学基金青年项目“基于负外部性治理的农地城市流转管制研究”(71303260);中南财经政法大学博士生科研项目“中低山区区域耕地资源安全研究”(2013B0813)
崔许锋,男,河南襄城人,中南财经政法大学工商管理学院博士生;蒋月华,女,河南商丘人,湖南师范大学资源与环境科学学院硕士生。
