基于K-means的北京地铁路网重要度聚类分析

高 勃，秦 勇,肖雪梅，祝凌曦

(北京交通大学 a.信息中心；b.交通运输学院，北京100044)

基于K-means的北京地铁路网重要度聚类分析

高 勃*a,b，秦 勇b,肖雪梅b，祝凌曦b

(北京交通大学 a.信息中心；b.交通运输学院，北京100044)

以图论为基础，以北京地铁为研究对象，结合地铁运营客流时空分布的特点，构建北京地铁有向加权路网模型；采用K-means聚类分析方法，根据地铁路网中车站和区间的两个基本的物理拓扑属性（度、介数），以及客运量对其进行分类，确定关键车站和区间.其中，度反映的是节点的局部聚集能力，介数反映的是节点和边对全局的影响能力，而客运量则反映了不同时间段节点和边在运输中的重要性.实证分析表明，该方法可以从系统网络的角度动态辨识系统中的关键车站和区间.

城市交通；重要度；K-means；地铁路网；异质性

1 引 言

地铁因其运量大、速度快、安全可靠等特点成为缓解城市交通需求矛盾的重要工具.随着地铁新线的不断规划、建设和投入运营，我国部分特大城市的地铁线路已进入网络化运营阶段.在地铁网络不断扩大的同时，路网客流量与日俱增，站与站之间关联性增强，局部问题对整个路网的波及效应和联动性更加突出.Sybil对世界上33个国家的地铁路网研究证明，地铁路网属于无标度网络[1].在蓄意攻击条件下，无标度网络非常脆弱.1%的“核心节点”一旦受到攻击失效，网络性能将下降50%左右[2].因此，研究地铁路网运营中的“核心节点”具有重要意义.

网络节点（边）重要度研究最早来源于图论中MVNP（最关键节点问题）和MVEP（最关键边问题）的研究.评估方法主要包括度、接近度、中心性、删除法和综合评估法等，目前已经在通讯网络、公路网等多个领域得到了应用[3,4].对于地铁路网而言，在对其关键车站和关键区间进行评估时，一方面要从物理拓扑结构的角度考虑车站、区间在路网中的作用和影响力；另一方面要考虑车站、区间在运营中所承载的客运量对路网的影响.

本文以北京地铁为研究对象，采用聚类分析方法，根据地铁路网中车站和区间的两个基本物理拓扑属性（度、介数），以及客运量对其进行分类，确定关键车站和区间.

2 北京地铁加权路网模型

2.1 模型构建

随着北京地铁路网规模的不断扩大，客流量持续增长，部分车站和区间的承载能力已达到饱和，路网运营风险增大.为确保路网安全、高效运营，需要对地铁路网中的关键车站和区间进行辨

2.2 节点属性

节点度是图论中最基本的测度指标之一，能够衡量节点在路网中的局部凝聚能力.节点度di表示G中与节点vi相关联的边的个数.节点vi连接的识、分析和管理监控，以便针对性地制定应急预案.

图1 2013年北京地铁路网图Fig.1 Beijing urban rail transit network in 2013

本文以2013年4月北京地铁路网（如图1所示，共15条线路、225个车站）为例，对其关键车站和区间进行聚类分析.基于网络理论和方法，以车站为节点，相邻车站的区间为边，区间断面客流量为边权重构建地铁加权路网模型.

地铁加权路网模型由集合G=(V，E)表示，其中：

（1）V代表节点（车站）的集合，V={vi}，i=1,2, ···，N，N表示路网中车站的数目；vi代表G中第i个节点，是拓扑结构和功能属性的集合，vi={di,bi, ci(Δt)}，其中：di表示第i个节点的度，bi表示第i个节点的介数，ci(Δt)表示单位时间内第i个节点的客运量.

（2）E代表有向边（区间）的集合，E={eij}，i, j=1,2,···，N，i≠j，N表示路网中车站的数目；边eij是由相邻节点vi和vj构成的有序对(vi,vj)、结构属性和权重构成的集合，eij={(vi,vj),bij,ωij(Δ t)}，其中：bij表示边eij的介数，ωij(Δt)表示单位时间内边的eij权重.边越多，节点vi度越大，其局部拓扑重要度越大.

对图1建模，得到全部225个车站节点度分布.其中，约13%的车站节点度值较大，西直门车站的节点度值最大（d=10），东单、呼家楼、崇文门、国贸等29个车站节点度值其次（d=8），均为换乘车站.车站连接的线路越多，车站节点度越大，节点度值较大的车站，在地铁网络中的重要度会较高.

乘客在选择公共交通出行时，总是期望乘坐最少的区间到达目的地.定义地铁加权路网模型中区间的距离为1，地铁加权路网模型中任意两点间的最短距离即为节点vs和节点vt间的最短路径中的边的个数.

节点介数(Betweenness Centrality)用来衡量节点在路网中的全局拓扑结构重要程度，反映了该节点在整个路网中的地位和影响力.

节点介数bi表示路网所有最短路径中经过节点vi的比例，即

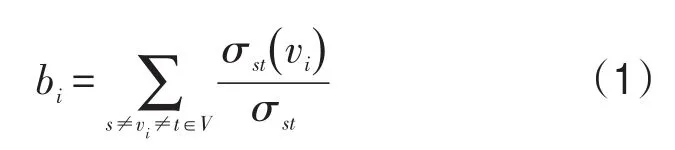
式中 bi——节点vi的介数；

σst——节点s到t的最短路径数量；

σst(vi)——节点s到t经过节点vi的最短路径的数量.

经计算，节点介数排名前15的车站如表1所示，其中西直门车站依然排在首位，部分换乘站如军事博物馆、建国门、宣武门、崇文门、知春路、白石桥南等在节点度、节点介数的指标上都排名居前；车公庄、朝阳门、大钟寺等非换乘站虽然在节点度的排名居后，但从节点介数分析，其重要程度甚至超过很多换乘车站；这表明车公庄、朝阳门等非换乘车站在路网中同样起到重要作用.

表1 不同车站节点介数Table1 Stations ranking by node betweenness

节点客运量ci(Δt)，单位时间内节点进站客流量、出站客流量和换乘客流量的总和：

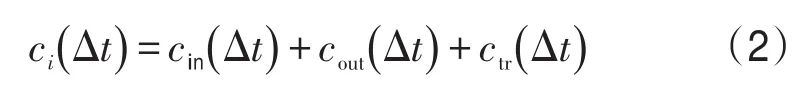
式中 ci(Δt)——节点客运量，单位：人次/小时；

cin(Δt)——单位时间内进站客流量；

cout(Δt)——单位时间内出站客流量；

ctr(Δt)——单位时间内换乘客流量.

表2列出了在早、晚高峰和平峰三个时间，段客运量排名前6的车站.

表2 不同时间车站节点客运量Table2 The stations ranking by volume

北京地铁客流具有典型的“潮汐”特点，早晚高峰期间客运量远大于其它平峰时段.拓扑属性相同条件下，客运量越大，运输地位越重要.不同时段，由于客流的走向和需求不同，车站客运量排序是不相同的.西直门、国贸、建国门、东直门等换乘站，在全天都是节点客运量较大的车站.

2.3 边属性

边介数bij反映了该边在整个路网中的地位和影响力，表示路网所有的最短路径中经过边eij的比例，即

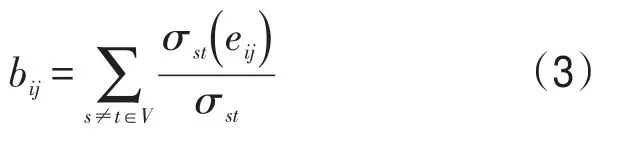
式中 bij——边eij的介数；

σst(eij)——节点s到t经过边eij的最短路径的数量.

边介数排名前15的区间如表3所示.

表3 不同车站区间边介数Table3 Intervals ranking by edge betweenness

边介数排名靠前的区间，都至少连接了一个换乘站.这说明，与换乘站相连的区间，在路网结构中具有较高的地位和影响力.

边权重ωij(Δt)表示单位时间内，单向通过运营线路特定方向的区间断面客流量，单位：人次/小时.单位时间内通过区间的断面客流量越大，区间权重越大，在路网运输中的地位越重要.

地铁的一个典型特点就是运输的方向性，同一时间同一区间上、下行区间断面客流量是不相同的，即ωij(Δt)≠ωji(Δt).图2为北京地铁某区间2013年3月某天不同时间段上下行的客运量，早晚高峰期间客运量大于平峰时段.虽然二者拓扑结构相同，但在客流运输中的重要程度是不同的，且随着时间的不同而变化.

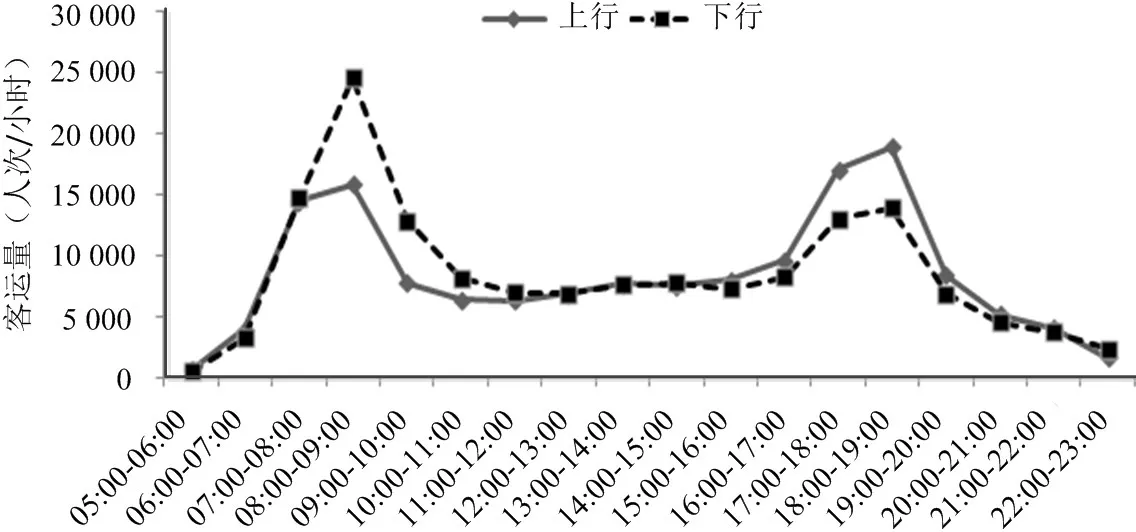
图2 某一区间上、下行全天不同时间段客运量Fig.2 The passenger volume of interval at different times

通过分析可知，考虑到客运量后，结构拓扑属性相同的节点和边，由于其承载的客运量不同，其功能属性及在路网运营中的地位是不同的.

3 车站和区间重要度聚类分析

3.1 关键节点（边）重要度定义

关键节点（边）是指对维持地铁加权路网正常运输起到重要作用的车站（区间）.路网中关键节点和边一旦失效，会导致路网连通性、路网运能大幅度下降；在极端情况下，部分关键节点和边失效，会导致路网结构和功能的整体失效.

K-means聚类算法，具有简单、高效等优点[5-7].本文应用K-means聚类算法，根据表征地铁路网中车站和区间的局部拓扑重要性指标（度）、全局拓扑重要性指标（介数），以及运输功能（客运量）进行聚类分析，确定关键节点和边.

3.2 基于K-means的重要度聚类分析算法

路网模型中各节点（或者边）构成样本集Y= {y1,y2,···,yi,···,yn}，其中，n是节点（或者边）的数量；每个样本yi={yi1,yi2,···,yid}，yid表示第i个节点（或边）的第d个属性值.

基于K-means的车站和区间重要度聚类分析基本步骤：

Step1确定分类数K.从整体样本Y中，随机选取K个对象作为初始的簇中心mj(I)(j=1,2,···, K)，令I=1.

Step2采用欧式距离作为相似度的衡量标准，计算Y中每个样本yi到K个簇中心的欧式距离d(yi,mj(I))，找到每个样本yi的最小d(yi,mj(I))，将yi归入到与mj(I)相同的簇中.

Step3遍历完所有对象之后，重新计算mj(I)的值，以簇中所有点均值作为新的簇中心.

Step4计算误差平方和E(I).

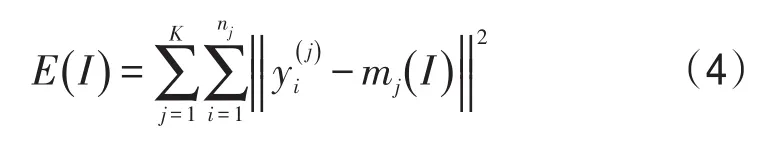
nj——第 j个簇中样本的个数.

若|E(I)-E(I-1)|<ξ则算法结束；否则I=I+1，返回Step2.

3.3 重要度分布异质性

研究表明，网络的异质性和脆弱性相关[7].信息熵用来衡量地铁加权路网模型的节点（边）重要度分布的异质性.地铁加权路网中节点和边的重要度分布越不均匀，熵值越大，重要度分布的异质性越大，整个路网的风险越高.

通过可靠性理论中的分组经验公式[8]确定节点和边重要度的分类数K：

式中 n——路网中节点或者边的总数.

重要度分布熵H代表网络中节点（边）重要度分布的不均匀程度.

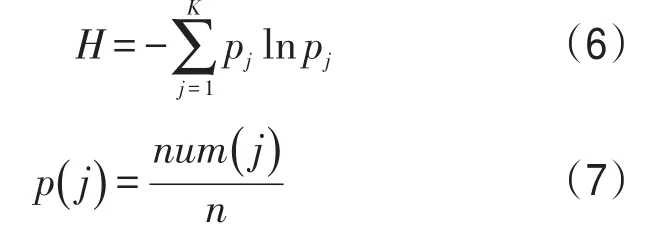
式中 pj——路网中重要度等级为j节点（或者边）的比例；

num(j)——重要度等级为j的节点（或者边）的数量.

4 聚类分析

选取北京地铁路网3月某一工作日三个时间段，分别是早高峰（8:00-9:00）、平峰（11:00-12:00）和晚高峰（18:00-19:00），对于车站以节点度、节点介数和节点客运量为变量，对于区间以区间介数、区间客运量为变量，进行重要度聚类分析.

为观察重要度的分布情况，根据分组经验公式K=1+3.3lgn，同时考虑到分组数一般是5或者10的倍数，将车站和区间分为10组.通过SPSS软件，分类数K=10，最大迭代数NC=10，收敛标准取0，聚类结果如表4和表5所示.

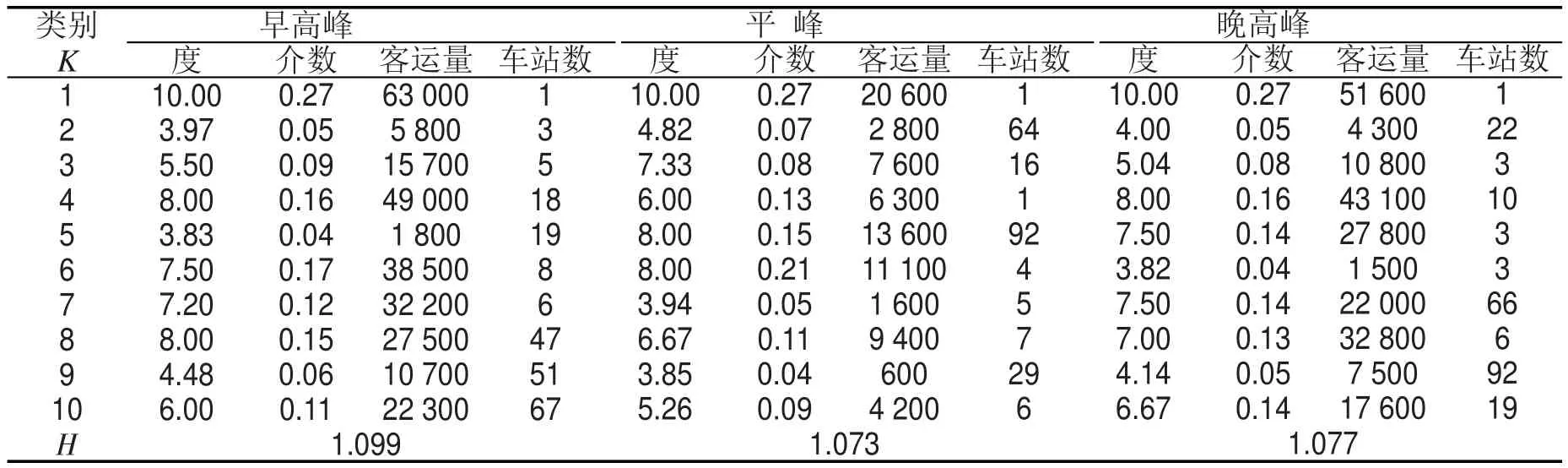
表4 不同时间车站聚类结果分析Table4 Clustering center at different times

表5 不同时间区间聚类结果分析Table5 Clustering center at different times

由表4、表5可知，由于不同时间段各车站和区间客运量的不同，不同时间段聚类中心各指标分类标准（均值）是不一样的.从而证明，结合物理拓扑和运输功能属性，采用K-means方法可以实现地铁路网车站和区间重要度的动态聚类分析.同一聚类中的车站和区间在物理拓扑属性和运输功能属性上具有较高的相似度，物理拓扑和客运量值均较大的聚类中的车站和区间对路网的正常运营起到关键作用.

以早高峰为例，车站K1聚类中的西直门站，以及区间K7聚类中的菜市口→陶然亭方向，无论其拓扑结构属性或者客运量都较大，其在路网运营中的地位非常重要.而车站K4聚类中的国贸站和K7聚类中的朝阳门、雍和宫和崇文门等站，以及区间K1聚类中的西直门→动物园方向和K5聚类中的北京西站→军事博物馆方向，虽然它们的拓扑结构属性相近，但是由于国贸站和西直门→动物园方向客运量较大，它们的重要性并不属于同一类，从而证明在对车站和区间重要度进行聚类分析时需要考虑客运量.通过对不同时间段路网中车站和区间重要度聚类发现，随着时间变化，客运量不断变化，路网中车站和区间的重要度异质性也是随之变化.如表4和表5所示，在早晚高峰期间重要度的分布异质性大于平峰时间，风险增加.

图3给出了，在不同时间段，度、介数和客运量都较大的聚类中的车站和区间名称，这些聚类中的车站和区间在路网拓扑结构，以及路网运输功能方面都发挥着重要作用.

图3 不同时段关键车站和区间Fig.3 The key stations and intervals at different times

由图3可知，在不同时间段，基于物理拓扑和客运量属性的各聚类中的车站和区间是动态变化的.例如：国贸站位于北京的中央商务区，西直门站处于2号线、4号线和13号线的交汇点，不论早晚高峰还是平峰时间，其在路网运营中的地位都极其重要；西单站位于北京的重要商业圈，平峰和晚高峰期间，在路网运营中的地位非常重要；西二旗站作为13号线和昌平线的换乘站，同时周边聚集了联想、百度、软件园等大型公司企业以及一系列居民住宅区，在早晚高峰期间运营地位同样很重要；区间西单至东单方向，由于其途径天安门西和王府井等旅游地点，在平峰时间段地位很重要.因此，在不同时间，运营管理部门应针对不同重点车站加强管理和监控，从而确保路网正常运营.

5 研究结论

本文在构建北京地铁加权路网模型的基础上，根据地铁路网中车站和区间的物理拓扑属性（度、介数）以及运输功能（客流量），应用基于K-means的节点（边）重要度动态聚类方法分析地铁网络，并从信息熵的角度分析其异质性.

通过对北京地铁路网的实证分析，验证了该方法的可行性和合理性.分析发现，在不同时间段，北京地铁车站和区间在路网中的重要度是动态变化的，路网中车站（区间）的重要度异质性也是随时间而改变的.北京地铁路网运营管理部门，在路网异质性较大的时间段内，对处于高聚类等级中的车站和区间应进行重点监控、管理，保障其正常运行.这对于确保路网结构安全、可靠，以及路网整体性能发挥具有重要意义.

[1]Sybil D,Christopher K.The complexity and robustness of metro networks[J].Physica A,2010，389:3678～3691.

[2]王延庆.基于接连失效的复杂网络节点重要性评估[J].网络安全技术与应用，2008（03）:59-61 1[WANG Y Q.Node importance evaluation of complex network based on successive failure[J].Net Security Technolo⁃gies and Application,2008(3):59-61.]

[3]陈静,孙林夫.复杂网络中节点重要度评估[J].西南交通大学学报，2009，44（03）:426-429.[CHEN J,SUN L F.Evaluation of node importance in complex networks [J].Journal of Southwest Jiaotong University,2009,44 (3):426-429.]

[4]Zhao K,Kumar A,Yen J.Achieving high robustness in supply distribution networks by rewiring[J].IEEE Transactions on Engineering Management,2011,58(2)：347-362.

[5]莫春玲.复杂网络中聚类方法及社团结构的研究[D].武汉：武汉理工大学,2007.[MO C L.The Research of clustering methods and community structure in complex networks[D].Wuhan University of Technology,2007.]

[6]黄韬,刘胜辉,谭艳娜.基于K-means聚类算法的研究[J].计算机技术与发展,2011,21(7):54-57,62.[HUANG T,LIU S H,TAN Y N.Research of clustering algorithm based on K-means[J].Computer Technology and Devel⁃opment,2011,21(7):54-57,62.]

[7]Zhao K,Kumar A,Harrison TP,et al.Analyzing the resil⁃ience of complex supply network topologies against ran⁃dom and targeted disruptions[J].IEEE Systems Journal, 2011,5(1)：28-39.

[8]赵宇,杨军,马小兵.可靠性数据分析教程[M].北京：北京航空航天大学出版社,2009.[ZHAO Y,YANG J, MA X B.Reliability data analysis[M].Beijing Universi⁃ty of Aeronautics and Astronautics Press,2009.]

K-means Clustering Analysis of Key Nodes and Edges in Beijing Subway Network

GAO Boa,b,QIN Yongb,XIAO Xue-meib,ZHU Ling-xib
(a.Information Center；b.School of Traffic and Transportation,Beijing Jiaotong University,Beijing 100044,China)

This paper modeled a subway system as a directed and weighted network with consideration of the temporal and spatial distribution of passengers in the subway system.Based on the K-means clustering, stations(nodes)and intervals(edges)in a subway network were grouped by three metrics:two basic topological properties(degree and betweenness),and their roles in transporting people(passenger volume).Degree reflects the nodes’local accumulation ability;betweenness reflects a node or edge’s the impact on the global network topology,and passenger volume reflects a node or edge’s importance in transport people at different times.Taking the Beijing Subway network as a case study,the paper tested the effectiveness of the proposed approach.The results suggested that the method could identify key nodes and edges and provide dynamic decision support for subway network operators.

urban traffic;key edges and nodes;K-means;subway network;heterogeneity

1009-6744（2014）03-0207-07

U121

A

2013-11-05

2014-05-02录用日期：2014-05-07

高勃（1980-），男，山东泰安人，工程师，博士生.*通讯作者：gaobo@bjtu.edu.cn