瓶颈路段上拥挤收费水平与收费时段的优化问题0

魏玉光，薛 莹，任华玲

（北京交通大学 城市交通复杂系统理论与技术教育部重点实验室，北京100044）

瓶颈路段上拥挤收费水平与收费时段的优化问题0

魏玉光＊，薛 莹，任华玲

（北京交通大学 城市交通复杂系统理论与技术教育部重点实验室，北京100044）

本文主要在瓶颈路段建立单一收费方案，并且优化瓶颈路段上的拥挤收费水平和收费时段.首先，应用Greenshields模型描述了瓶颈路段上流量的演化过程，并计算每个时刻出行者的出行时间和出行费用.通过出行费用与流量的关系调整每个时刻流量的分配，得到稳定状态时排队的长度和运动部分的速度.然后，建立双层规划模型，其中上层模型是最小化最大排队车辆数和最大化运动部分的最小速度，下层模型是应用Greenshields模型模拟出行者的出行行为.应用改进的遗传算法求解双层规划模型，得到最优的收费水平和收费时段.最后，应用一个简单的算例来验证本文所建立的模型及其算法，并且通过变换参数来分析所得到的现象和结论.

城市交通；拥挤收费水平；拥挤收费时段；Greenshields模型；双层规划；瓶颈

1 引言

小汽车保有量的迅速增加使得很多城市都出现了严重的交通拥堵.影响了人们的出行、环境的质量及城市的规划.1975年新加坡率先实施拥挤收费政策，1998年成为全球第一个实施公路电子收费的城市.2003年英国伦敦开始实施拥挤收费政策，收费区域主要集中在城市中心区.2006年斯德哥尔摩开始实施拥挤收费政策，经过6个月的试运行，证明拥挤收费政策确实能够缓解交通拥堵情况[1].

而我国如北京、上海、成都、香港等地都出现了不同程度的交通拥堵[2].但是由于产生交通拥堵的地区较多，地理位置较分散，因此很难在某一段区域实施拥堵收费政策.

多数的动态拥挤收费模型的拥挤收费是随时间连续变化的，以获得最优的社会效益.然而，现实中难以实施.尽管动态拥挤收费可以完全消除排队时间，但却存在很多实际问题，如收费决策体系不完善和收费统计成本过高等.因此分段收费方案成为替代的减少拥挤排队的收费方案.

Lindsey R等研究了瓶颈路段拥堵排队的分步收费模型[3].Arnott等研究了瓶颈路段的分段收费模型[4].这种模型的平衡状态假定收费结束时有大量的出行者选择出行，同时每个出行者选择出行的位置是随机的.Laih的分段收费模型则可以避免收费结束时大量出行者选择出行的问题[5].此外，还有其它的瓶颈路段分段收费模型.Van der Zijpp和Koolstra研究的在同一瓶颈路段多用户出行者对出发时间选择的相互作用，高峰期拥挤收费方案对出发时间的选择和每类出行者总费用的影响[6].此外，还有其它的瓶颈路段分段收费模型，以及对于异质出行者早高峰出行行为的研究[7，8].

上述的单一收费模型都是通过解析方法求得的，并基于车辆没有长度的假设，这种假设既不实用也很难应用于一般网络中.本文基于Greenshields模型[9]建立了一种单一收费的模型，应用双层规划模型优化收费水平和收费时段，并且最小化排队车辆最大值和最大化运动部分的最小速度.

2 基于Greenshields模型的单一收费模型

本文提出了基于Greenshields模型的单一收费模型.在该模型中，车辆是有正常长度的，在路段上行驶的车辆满足Greenshields模型的速-密关系，排队车辆的长度即为排队部分的长度.这种假设更适合于将收费方案推广到一般路网中.

2.1 模型的符号

在瓶颈模型中D为同一类型出行者的总需求量，出行工具即为小汽车（每人每车），从存在拥挤排队现象的瓶颈路段起点出发行驶到路段的终点.

下面先给出本文所需要的符号：

L——路段长度；

X(t)——t时段路段上的车辆数；

u(t)——t时段路段入口处的流入率；

v——瓶颈处的通过能力；

X2(t)——t时段路段上排队部分的车辆数；

r(t)——t时段路段上运动部分的速度；

rmax——路段上的最大行驶速度；

rmin——路段上的最小行驶速度；

kj——路段上的阻塞密度；

k1(t)——t时段路段运动部分的密度；

C(t)——t时段进入路段的车辆的出行费用；Cmin——最小出行费用；

Ctoll——路段上的拥挤收费水平；

t(t)——t时段车辆进入路段的总出行时间

t1(t)——t时段路段运动部分的行驶时间；

t2(t)——t时段路段排队部分的延误时间；

[t+，t-]——收费时段；

[wl，wr]——上班开始时间区间（此时段内没有早到和迟到惩罚）；

α——出行时间的单位费用；

β（γ）——早到（迟到）惩罚的单位费用.

2.2 Greenshields模型

在本文中，我们只考虑了瓶颈部分和某一段时间[0,T]，设定上班开始时间区间为[wl,wr].根据Greenshields模型可知，人们在wl之前到达会有早到惩罚，在wr之后到达会出现晚到惩罚.为避免出现严重的交通拥堵情况，我们选择在某一时段[t+,t-]内收取一定的拥挤费用.动态路段出行时间分为两部分：运动行驶时间和排队延误时间.

车辆在t时刻进入该路段后，该路段上的车辆数与t-1时刻的流入率和瓶颈处通过能力v以及t-1时刻的车辆数之间满足如下关系[10，11]：

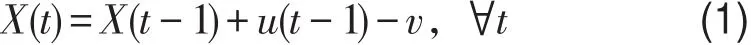
则t时刻排队长度为

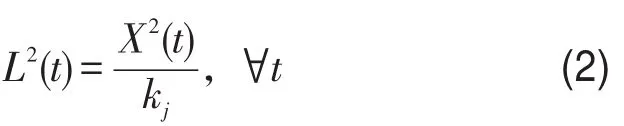
t时刻运动部分的密度为

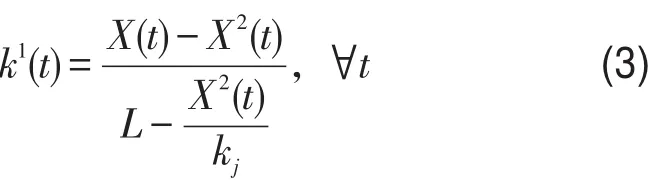
车辆在t时段进入该路段后，该路段上的排队车辆数X2(t)与t-1时刻的排队车辆数和瓶颈处通过能力v，以及t-1时刻的运动部分的速度和密度存在如下关系：可以得到t时刻该路段的出行时间为

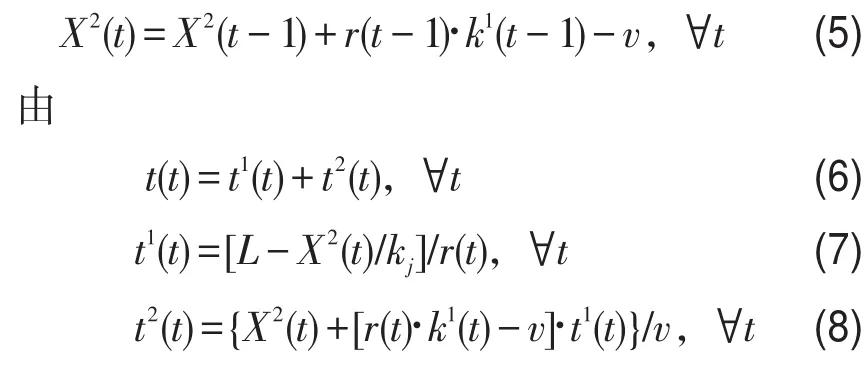
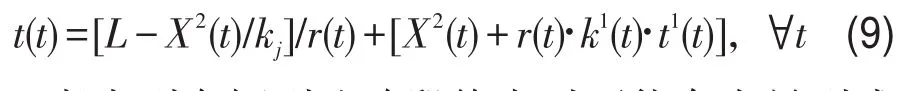
考虑到车辆到达路段终点时可能存在早到或晚到惩罚，定义该路段的出行费用如下[9，12-14]：

则t时刻运动部分的速度为

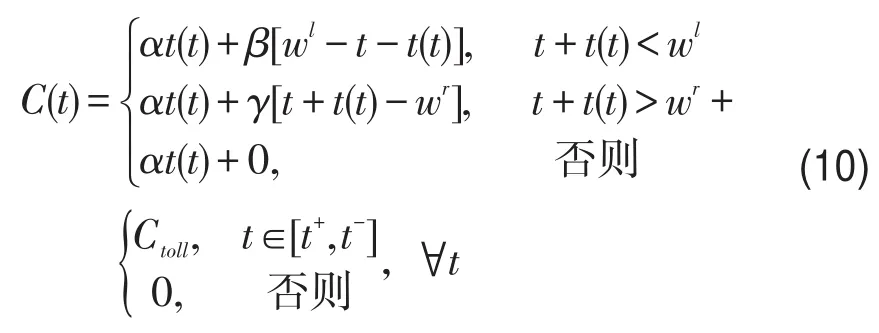
式中 α为出行时间的单位成本；β为早到惩罚的单位成本；γ为晚到惩罚的单位成本.根据经验取值γ＞α＞β.

根据用户平衡原则调整路段上人们对于出行时间的选择，达到稳定状态时：任何有出行者选择出发的时段，其出行者出行费用都相等并且等于最小出行费用；同时在其他任何时段，其出行费用皆大于最小出行费用.为了达到稳定状态，每个时刻的流入率需根据出行费用调整，循环过程概述如下：

第1步设OD需求量为D，收费水平为Ctoll，收费时段为[t+,t-].

第2步给定初始的流入率 u(t)1，满足，迭代次数n=1.

第3步根据式(1)、式(5)可以计算路段上的车辆数和排队部分的车辆数，其计算过程如下：

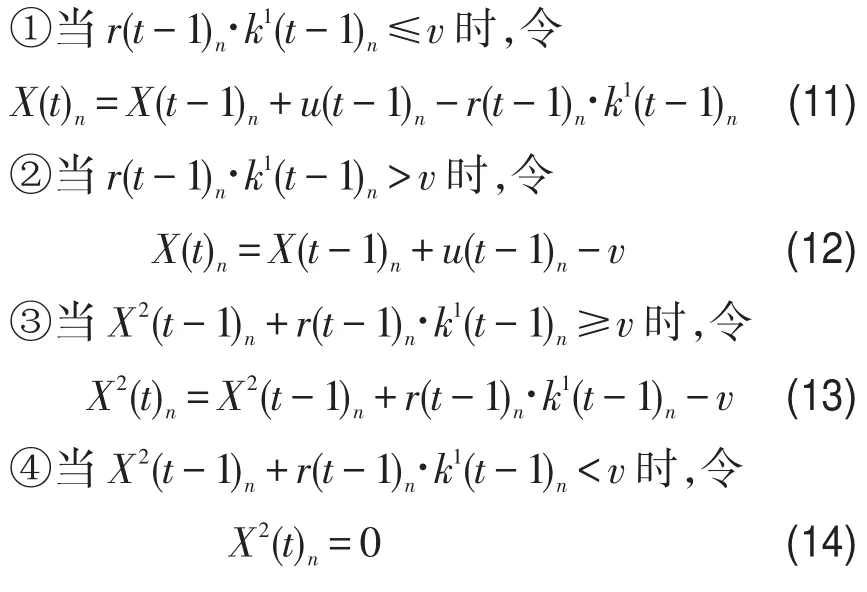
第4步根据式(9)计算t时刻出发的车辆在该路段上的出行时间为

第5步根据式(10)计算各个时刻出发的车辆在该路段上的出行费用，并找出其中最小的出行费用Cmin及等于最小出行费用的时段数|Cmin|.

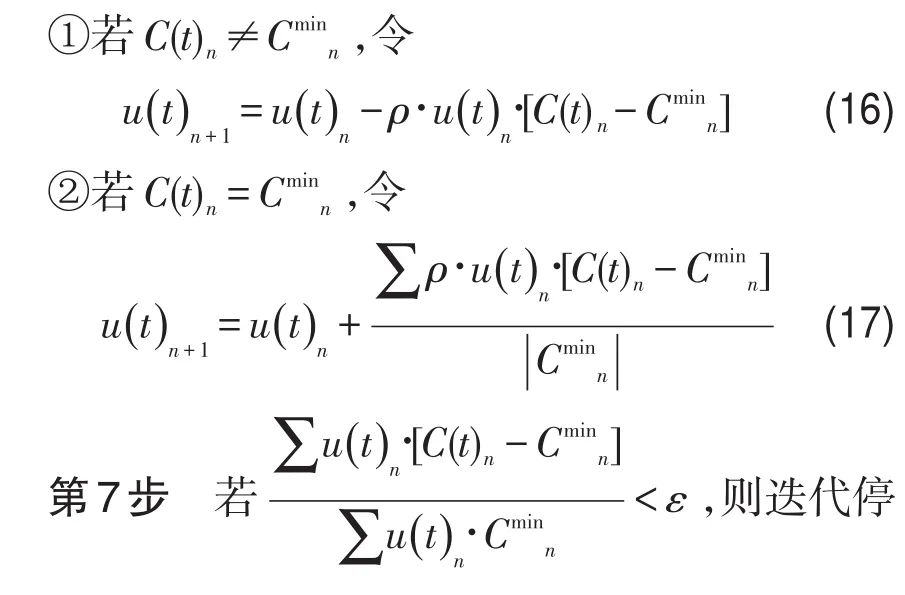
第6步各个时刻根据出行费用及最小出行费用更新流入率：止；否则，置n=n+1返回第3步继续迭代[10，11].

2.3 Greenshields模型的算例

本节通过一个简单的算例来应用Greenshields模型，得到Greenshields模型达到稳定时各个时段路段上的排队车辆数和运动部分的速度.

给定一条瓶颈路段，路段长度L为5.25 km，交通需求为625辆，路段上自由流速度为0.7 km/min，最小速度为0.3 km/min，可知路段上以自由流速度出行的时间为7.5 min.路段临界密度为56车/km，拥挤密度为160车/km，则可知瓶颈的通过能力为15车/min[11].除此之外设定其他参数：a=1，b=3，α=1,β=0.22,γ=2,ρ=0.000 1.[wl，wr]=[75,85]，[t+,t-]=[55,75].收取的费用为2.

图1-图4分别为各个时刻路段的流入率、出行费用、排队的车辆数、运动部分的速度.由于在收费开始前存在早到惩罚，因此选择出行的人较少，路段上不会产生拥堵排队，运动部分的速度也比较高.当接近收费开始时间t+=55时，出行者的数量开始降低，但由于之前有大量出行者选择出行，路段上的排队车辆数增加，运动部分的速度降低，出行者的出行费用会提高.当 t=t+=55时开始收费，突然增加的收费，加之此时的运动部分速度的降低，使得收费开始时刻t+附近的出行费用比稳定状态时略高.因此流入率降低为零，排队车辆数减少，运动部分的速度有所提高.（如图3和图4收费开始时间t+附近的几分钟）.随后，部分的出行者已经行驶到瓶颈处，排队车辆数开始增加，运动部分的速度开始提升，流入率开始快速增加.当t-=75时收费结束，出行者会选择此时出发以降低出行费用，因此会有流入率的突增.但此时排队正在消散，因此运动部分的速度仍然很高(如图4).

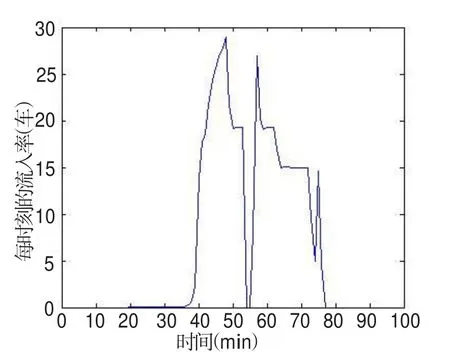
图1 路段上的流入率图Fig.1 The inflow rate on the road

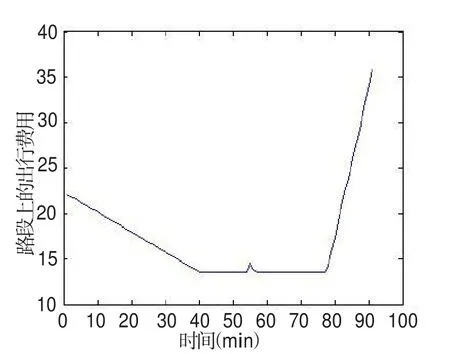
图2 路段上的出行费用Fig.2 The travel cost on the road

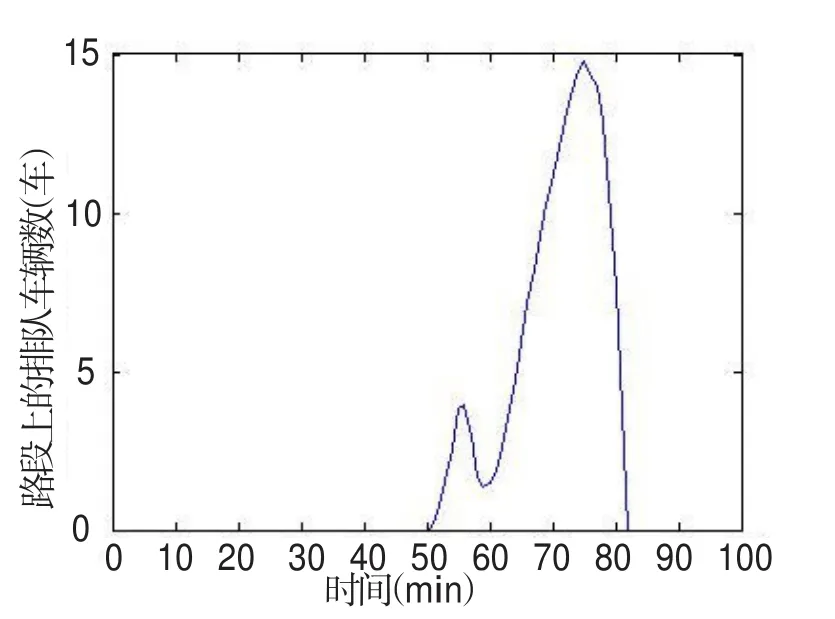
图3 排队部分的车辆数Fig.3 The number of queuing vehicles

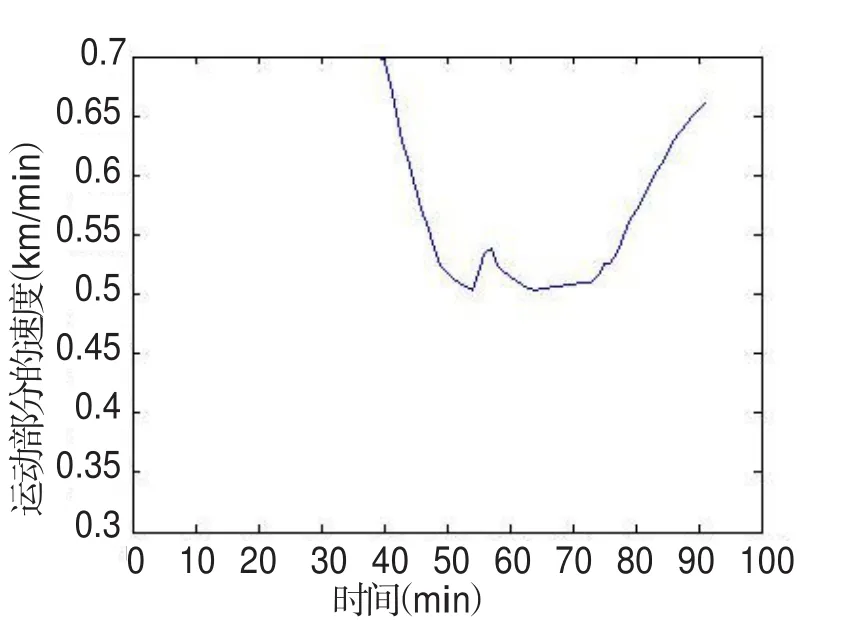
图4 运动部分的速度Fig.4 The speed of moving part

通过Greenshields模型的计算过程，可以得到稳定状态下每个时刻路段上的排队车辆数，以及出行者的出行费用.从图3和图4可以得到最大排队车辆数和最小行驶速度，本文将通过优化最大排队车辆数和最小行驶速度以得到最优的拥挤收费水平和收费时段.

3 优化模型及模型算法

3.1 优化模型的建立

通过Greenshields模型可知，路段上排队部分的车辆数X2(t)，以及路段运动部分的行驶速度r(t)均为拥挤收费水平Ctoll、收费开始时间t+和结束时间t-的函数.根据Greenshields模型中的关系，通过优化收费水平和收费时段可以最小化排队部分的车辆数X2(t)，以及最大化运动部分的速度r(t).因此在此部分提出了双层规划模型，上层规划目标函数是最小化最大排队车辆数与最小运动部分速度之差.下层规划目标函数则为一定收费水平和收费时段下的Greenshields模型.上层的决策变量为收费水平和收费开始时间以及收费结束时间，下层决策变量为各个时刻的路段流入率.

本文建立的上层模型如下：

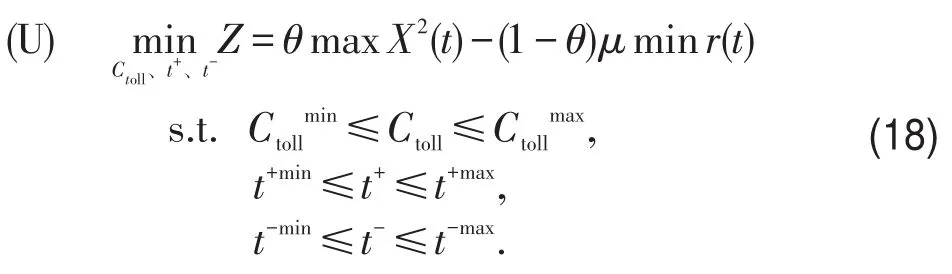
实际应用中收费水平有一定的限制.收费开始时间不早于排队开始时间，不晚于恰好在上班时间到达的出发时刻.收费结束时间不早于排队结束时间，不晚于上班开始时段的结束时间.X2(t)和r(t)的值由下层Greenshields模型求得，θ为权重系数，μ为转换系数.

对于任何一种上层决策的收费方案，只要确定了上层的决策变量Ctoll、t+和t-，下层Greenshields模型中都有一个用户平衡状态与之对应.因此，通过改进的遗传算法，在不同的上层决策变量下，求得相应的下层规划的结果，用于确定上层决策变量更新的依据，经过迭代过程，最终使得上层的决策变量逐渐靠近最优解.

3.2 优化模型的求解过程

本文应用遗传算法来求解双层规划模型[15，16]，算法的求解过程如下：

第1步设定遗传算法中的相关参数：交叉概率pc，变异概率pm，最大进化代数MaxGen，每一代的种群个数m(m为偶数).

第2步随机产生m个符合上层约束集的种群、t+(0)和t-(0)，初始进化代数N=0.

第3步将上层模型的目标函数作为适应度函数 fitness，对上层决策变量进行(0～m)的实数编码，根据2.2节求解下层Greenshields模型，然后返回上层计算个体的适应度.若此时N=MaxGen，则适应度排名最大的为最优解.否则转到第4步.

第4步采用基于排名的轮盘式选择算子及精英模型复制选择下一代种群、t+(N)和 t-(N).具体过程如下：

第4.1步计算每个个体的适应度函数值，将适应度函数值 fitness(i)按从优到劣的顺序排列，并

第4.2步计算每一个个体被选择的概率pi=fitness(i)/S.

第4.3步根据轮盘赌方式，随机产生(0～1)之间的随机数e1，若pi＜e1，则复制个体，否则淘汰.

第5步根据交叉概率pc，进行交叉操作.对种群中所有个体随机配对，对每一配对产生(0～1)的随机数e2，若e2＜pc，则进行交叉操作.交叉过程如下：

第5.1步对于每一对g1,g2，产生(0～1)的随机数c.

第5.2步进行交叉：

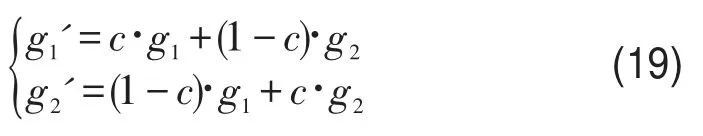
式中 g1',g2'为新个体；g1,g2为当前的两个个体.

第6步根据变异概率进行变异操作.过程如下：

第6.1步对种群中的每一个个体，产生(0～1)的随机数e3.

第6.2步若e3＜pm，则该个体发生如下变异：

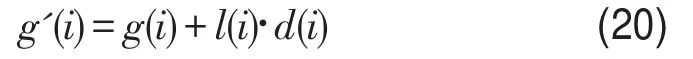
式中 l(i)为变异步长，l(i)∈max[g(i)max-g(i)min] (i=1,2,...,m,g(i)max、g(i)min分别为该个体取值的上限和下限)；d(i)为随机产生的变异方向，d(i)∈[-1,1].

第6.3步令N=N+1，返回第3步继续迭代.

4 数值算例

本节仍应用3.3节算例中给出的各种参变量，应用本文建立的收费水平和收费时段优化模型及求解方法，并对数值结果进行分析.

收费水平的约束范围为[1,10]，收费开始时间的约束范围为[40,60]，收费结束时间的约束范围为 [70,90].改进的遗传算法中的参数设定：pc=0.6，pm=0.1，m=20，MaxGen=50，θ=0.6，μ=10.

基于以上数据，本文考虑了三种收费优化方案：

(1)只将路段排队部分的车辆数的最大值最小化作为上层模型的优化目标函数.

(2)只将路段运动部分的最小速度最大化作为上层模型的优化目标函数.

(3)同时考虑运动部分最小速度最大化和排队车辆数最大值最小化的情况.

根据以上三种方案，分别求出三种方案下的最优解：

(1)Ctoll=4.9136,t+=46,t-=79

(2)Ctoll=4.9136,t+=44,t-=79

(3)Ctoll=5,t+=45,t-=80

从图5可知，当只考虑方案(1)时，尽管此方案下排队车辆数的最大值是三种方案中的最小值.但由于排队车辆数较小，人们的出行费用降低，会导致此时段的流入率增大，运动部分的密度增大，因此运动部分的最小速度降低.从图6和图7可知，此方案下，运动部分的速度最小值较其它两种方案都低.而当只考虑第(2)种方案，虽然此方案下的最小速度为三种方案中最大的，但此方案下排队的车辆数最大值却是三种方案中最大的，排队车辆数最大值没有得到优化，在收费结束后产生了严重的拥堵.因此，本文上层模型考虑第(3)种方案，将排队车辆数最大值和运动速度最小值同时优化，虽然此方案下最小速度没有第(2)种方案大，但相对于第(1)种方案最小速度得到优化，并且拥堵时段的速度变化较平缓.而且，第(3)种方案中排队车辆数的最大值虽然比第(1)种方案中的大，但此方案下的最小速度比第(1)种方案大.相对于第(2)种方案，此方案下的排队车辆最大值比较小.应用第(3)种方案缓解瓶颈路段的交通拥堵，在减少其最大排队车辆数的同时也提高了严重拥堵时的最小速度.并且得到此模型下上层优化模型的最优解Ctoll=5,t+=45,t-=80.

图5 路段上排队部分的车辆数Fig.5 The queuing vehicles on the road

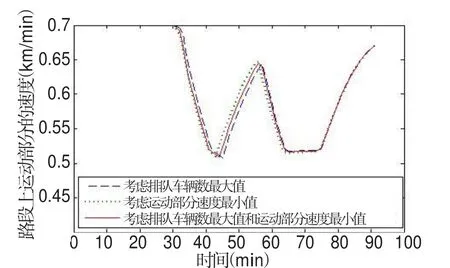
图6 路段上运动部分的速度Fig.6 The speed of moving part

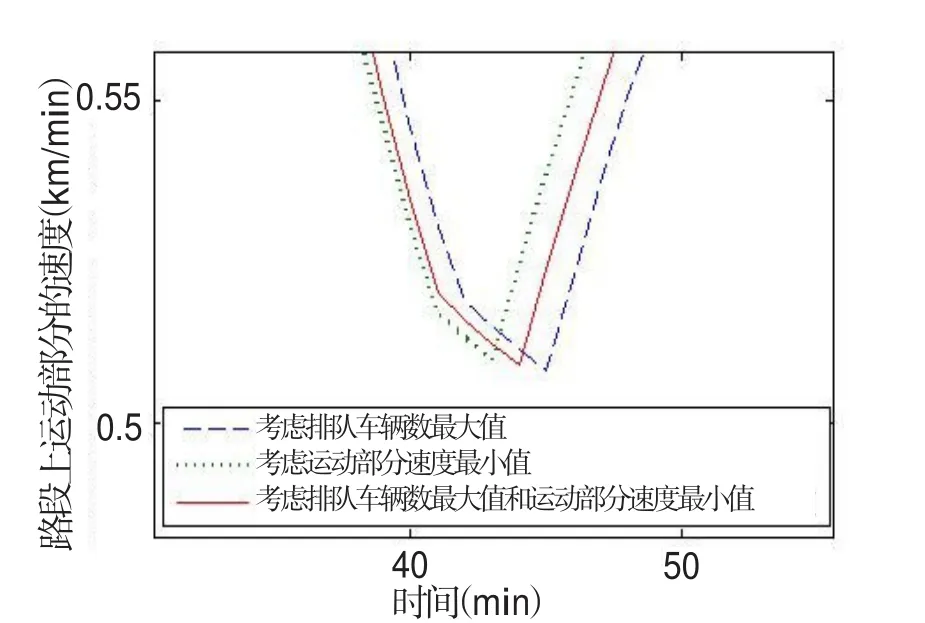
图7 运动部分的最小速度(图6中最低点的截图)Fig.7 The minimal speed(The part figure of Fig.6)

本文建立的优化模型中存在权重系数θ，权重系数θ的大小反映了优化目标中对排队车辆数的最大值和运动部分的行驶速度最小值这二者的重视程度.权重系数θ较小时，根据适应度函数计算式(18)可知，比较重视提高运动部分的最小速度.可知当权重系数θ由小变大时，模型在优化过程中考虑速度最小值的程度越来越小，因此，最优的运动部分最小速度会降低(见图8).

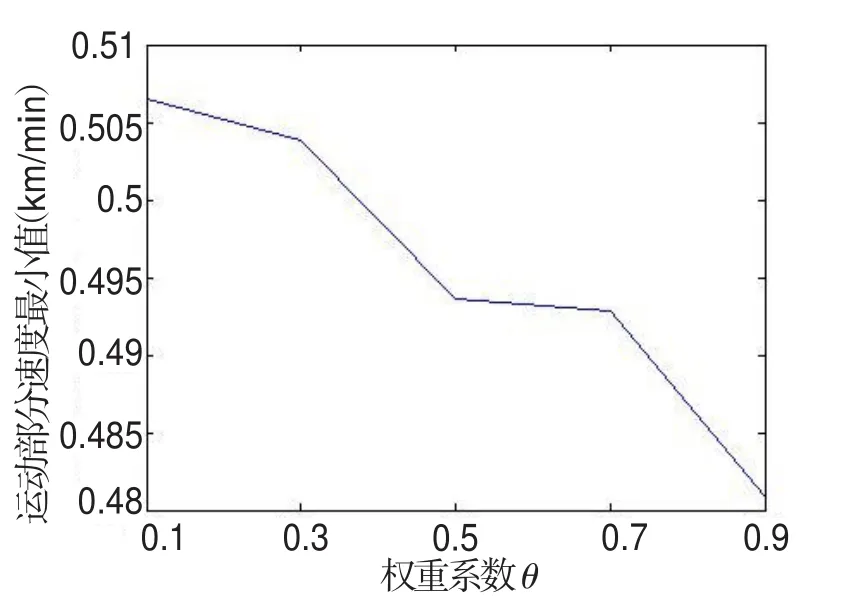
图8 运动部分速度的最小值-权重系数变化曲线Fig.8 Minimal speed-weighting coefficient curve

图9为取不同权重系数θ时，路段上每个时段出行者的出行费用.每个θ值下，在路段上开始收取拥挤费用后的一段时间，由于出行费用突然增加，而没有出行者出发.

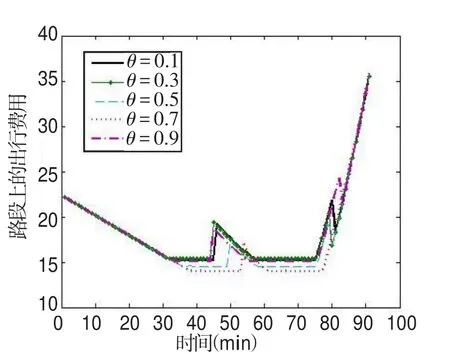
图9 路段出行费用-权重系数变化曲线Fig.9 Travel cost-weight coefficient curve

权重系数取不同值时，得到的最优解如下：

(1)θ=0.1时，Ctoll=5,t+=46,t-=80

(2)θ=0.3时，Ctoll=5,t+=45,t-=79

(3)θ=0.5时，Ctoll=4,t+=49.164 1,t-=79.606 8

(4)θ=0.7时，Ctoll=4,t+=53.465 4,t-=73.293 1

(5)θ=0.9时，Ctoll=4.351 1,t+=44.893 4,t-=82

由这些结果可知当权重系数改变时，直接会影响最优收费水平和收费时段的改变.并且发现，当权重系数为θ=0.7时，不仅最优收费水平是最低的，而且最优收费时段是最短的，个人出行费用也是最小的.也就是说，同时考虑排队部分车辆数和运动部分速度的优化是更为合适的.

5 研究结论

在本文中，应用Greenshields模型更真实地描述出行者的出行行为.基于Greenshields模型建立了单一收费模型，来描述收费对于人们出行行为的影响.进而建立双层规划模型，上层模型为最小化排队车辆数的最大值和最大化运动部分的最小速度，下层模型为基于Greenshields模型的单一收费模型.应用遗传算法对双层规划模型进行求解，得到最优的收费水平和收费时段.利用本文建立的模型，通过算例对三种收费方案进行求解，并分析了收费方案的作用.

本文只考虑了路段上只存在同一类型的出行者，今后将会考虑路段上存在多种类型出行者的情况，如何将此模型应用于一般路网中也是需要进一步研究的方向.

[1]王喜文,赵胜川.世界主要城市交通拥挤收费概述[J].中国科技论文在线,2008,3(10):746-750.[WANG X W,ZHAO S C.A summarization of the transportation congestion pricing in the main cities of the world[J].Sci⁃ence Paper Online,2008,3(10):746-750.]

[2]陈宁.城市中心区交通拥堵收费探讨—以成都市为例[J].广州大学学报(自然科学版),2009,8(5):91-94. [CHEN N.The study on congestion charge in central ur⁃ban district-Take Chengdu for an example[J].Journal of Guangzhou University(Natural Science Edition), 2009,8(5):91-94.]

[3]Lindsey R,Van den Berg V，Verhoef E.Step tolling with bottleneck queuing congestion[J].Journal of Urban Eco⁃nomics,2012,72(1):46-59.

[4]Arnott R,De Palma A，Lindsey R.Economics of bottle⁃neck[J].Journal of Urban Economics,1990,27(1):111-130.

[5]Laih C.Queuing at a bottleneck with single and multistep tolls[J].Transportation Research Part A,1994,28 (3):197-208.

[6]Van der Zijpp N，Koolstra K.Multiclass continuoustime equilibrium model for departure time choice on sin⁃gle-bottleneck network[J].Transportation Research Re⁃cord,2002,1783:134-141.

[7]Lindsey R,Van den Berg V，Verhoef E.Step tolling with bottleneck queuing congestion[J].Journal of Urban Eco⁃nomics,2012,72(1):46-59.

[8]Qian Z，Zhang H M.The morning commute problem with heterogeneous travelers:the case of continuously distrib⁃uted parameters[J].Transportmetrica A:Transport Sci⁃ence,2013,9(2):178-203.

[9]Ren H L,Gao Z Y,Lian A P.Dynamic user optimal as⁃signment problem based on Greenshields model[C]// Traffic and Transportation Studies Proceedings of ICTTS 2006,2006,326-335.

[10]Huang H J,Lam W H K.Modeling and solving the dy⁃namic user equilibrium route and departure time choice problem in network with queues[J].Transportation Re⁃search Part B,2002,36(3):253-273.

[11]Chris M J T,Francesco V,Lambertus H I.New develop⁃ments in transport planning[M].Edward Elgar,2010.

[12]Ren H L,Gao Z Y,Lam W H K,et al.Assessing the ben⁃efits of integrated en-route transit information systems and time-varying transit pricing systems in a congested transit network[J].Transportation Planning and Technol⁃ogy,2009,32(3):215-237.

[13]Gao Z Y,Song Y F.A reserve capacity model of optimal signal control with user-equilibrium route choice[J]. Transportation Research Part B,2002,36:313-323.

[14]Yang H,Huang H J.Mathematical and economic theory of road pricing[M].Elsevier,2005.

[15]陈来荣,张岚.基于双层规划的拥挤定价模型及算法[J].北京工业大学学报,2006,32(5):526-529.[CHEN L R,ZHANG L.Congestion pricing model and algorithm based on bi-level programming model[J].Journal of Bei⁃jing University of Technology,2006,32(5):526-529.]

[16]田小梅,龚静.实数编码的遗传算法评述[J].湖南生物职业技术学院学报,2005,11(1):25-31.[TIAN X M, GONG J.On overview of real-coded genetic algorithm [J].Journal of Hunan Environment-Biological Polytech⁃nic,2005,11(1):25-31.]

Optimization of the Tolling Level and Tolling Period for Bottleneck Model

WEI Yu-guang,XUE Ying,REN Hua-ling
(MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Beijing Jiaotong University,Beijing 100044,China)

This paper mainly analyzes the problem of step-toll on a bottleneck link and optimizes the level and period of congestion pricing in single-step-toll method on a bottleneck link.Firstly,based on Greenshields model,this paper describes the propagation of flow on the bottleneck link,and calculates the travel time and the travel costs of the travelers’departing at each time.The flows of all the time are adjusted by the relationship between total trip costs and flows until the flows reach the UE equilibrium.And Greenshields model is applied to obtain the queue length and the speed of the moving part at a stable state.Then,the bi-level programming model is established,in which the upper level is to minimize the maximal queue length and to maximize the minimal speed,and the lower programming is to simulate the travel behaviors using the Greenshields model.The bi-level programming model is solved by an improved genetic algorithm,to obtain optimal pricing level and pricing period.Finally,a simple example is given to illustrate the application of the model and the algorithm.The phenomena and conclusions are analyzed by transformation parameters based on optimal pricing level and pricing period.

urban traffic;tolling level;tolling period;Greenshields model;bi-level programming model; bottleneck model

1009-6744（2014）03-0179-08

U491

A

2013-11-13

2014-01-15录用日期：2014-01-29

国家自然科学基金(71371026).

魏玉光（1967-），男，江苏赣榆，副教授，博士.*通讯作者：ygweich@bjtu.edu.cn