基于球磨机的LS-SVM广义逆内模控制研究

孙灵芳 李 丹

(东北电力大学自动化工程学院，吉林 吉林 132012)

球磨机制粉系统是火力发电厂里典型的多输入多输出系统，由于它具有非线性、强耦合特性，且至今难以实现多变量系统的稳定闭环控制[1]。因此，球磨机系统的自动控制问题仍是国内外学者研究的重点和难点。

针对球磨机系统的控制问题，常规的控制方法是PID(Proportional Integral Derivative)控制，其优点是控制模块简单，易于工程实现，但它的适应性差，难以跟踪现场实时变化趋势。随着智能控制的飞速发展，将先进控制与常规控制相结合的复合控制方法为解决这类问题提供了一条新的途径。如粒子群BP神经网络PID优化算法[2]、模糊径向基神经网络PID算法[3]及专家模糊PID算法[4]等，这些算法复合了先进控制与常规控制两者的优点，效果优于PID控制，但它们都以简化球磨机模型为前提进行仿真分析，即球磨机是一个典型的三输入三输出系统，上述算法均先分解成一个双输入双输出被控对象和一个单变量被控对象，而简化的模型与原模型存在的误差问题未予考虑。若采用上述方法对球磨机三阶模型进行控制仿真将导致系统稳定性变差，为解决这一问题，笔者采用LS-SVM广义逆内模控制方法。由于LS-SVM可以在小样本条件下精确辨识非线性系统[5]，利用LS-SVM辨识球磨机的广义逆系统，避免了模型误差问题，与原系统串联后构成开环控制的伪线性系统可以实现不完全解耦控制，最后引入内模可以提高闭环控制回路的鲁棒稳定性。

1 LS-SVM广义逆内模控制算法①

1.1 LS-SVM简介

Suykens和Vandewalle提出的SVM(Support Vector Machine)算法，其基本思想是：通过非线性映射φ(x)把训练样本从低维空间映射到高维空间，在高维空间建立线性回归函数。

给出训练样本集{(xi,yi),xi∈Rn，yi∈R}，i=1,2,…，n，则LS-SVM的回归线性输出为：

y(x)=ωTφ(x)+b

(1)

式中b——偏置量；

ω——特征空间中具有相同维数的权向量；

φ(x)——非线性映射。

对式(1)进行函数预估，引入Lagrange函数，其中αi为Lagrange乘子，通过Karush-Kuhn-Tucker(KKT)条件简化，从而得出LS-SVM的非线性回归模型为：

(2)

1.2 广义逆系统

逆系统是将非线性系统反馈线性化的一种常用方法，由逆系统发展起来的广义逆系统与原系统串联构成的伪线性系统，不但解决了原系统的耦合问题，而且通过合理地配置广义逆系统参数使复合系统稳定，且易于实现。此外，广义逆系统可以使高阶系统不用降阶而直接实现解耦控制，避免了模型因降阶而导致的误差问题，如图1所示。

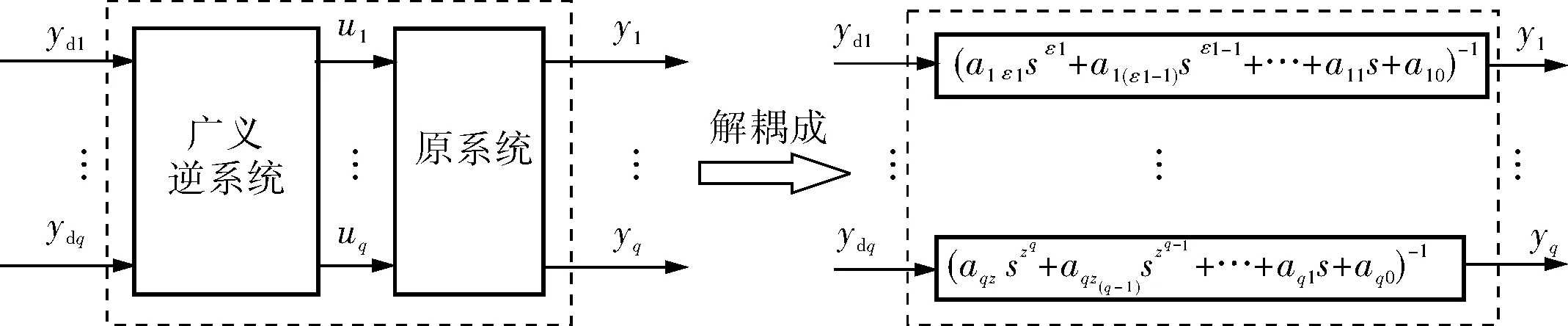
图1 广义逆系统的线性化与广义逆伪线性复合系统

1.3 内模控制

由Garcia和Morari完整地提出并发展的内模控制(Internal Model Control，IMC)，由于其具有结构简单、参数整定直观明了、鲁棒性可在线调整及控制性能优越等优点，被广泛应用到多输入多输出系统和非线性过程中，其原理图如图2所示。

图2 内模控制原理

2 LS-SVM广义逆内模离散控制在球磨机系统上的应用

2.1 球磨机数学模型

笔者从机理法出发，以华润某电厂单元机组配备的MGS4060型双进双出钢球磨煤机为例建立相应的平衡方程[6]，可得球磨机数学模型为：

(3)

8438]·(273.15+tm)/273.15/134000}2

(4)

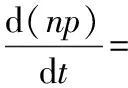
8438]·(273.15+tm)/273.15/134000}2

(5)

其中，tm、dp、np分别为球磨机出口温度、进出口差压和入口风压；Bgm、Gr、Gl分别为给煤量、热风量和冷风量。根据逆系统理论和Interactor算法，该模型的可逆性存在。

2.2 算法分析

根据球磨机的数学模型可知，该模型是一个典型的三输入三输出且带有强耦合的非线性系统。笔者采用LS-SVM广义逆系统与内模控制相结合的方法进行控制研究。

分析原系统的广义逆系统，并与原系统串联成伪线性复合系统。为了建立3个最简的一阶子系统，通过设置基本系数得到的伪线性系统如图3所示。

图3 LS-SVM辨识的伪线性复合系统

用LS-SVM辨识广义逆系统，具体步骤为：

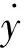
b. LS-SVM参数确定。选RBF核函数为K(x,xi)exp{-‖x-xi‖2/2σ2}，惩罚因子C和核函数参数σ。

由于LS-SVM广义逆系统是一个开环控制系统，许多不确定因素会导致系统输出不稳定或控制性能变差，因此引入内模控制形成稳定的闭环控制系统，如图4所示。

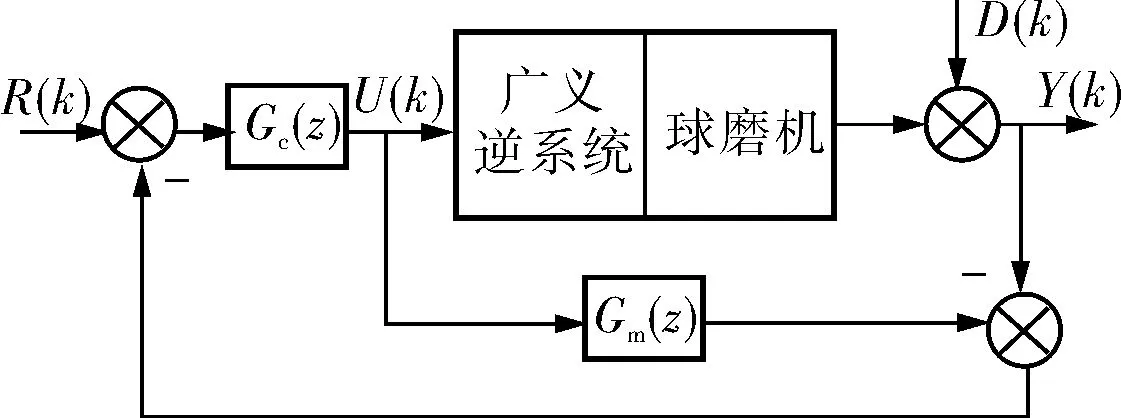
图4 LS-SVM广义逆内模控制框图

图4中，R(k)、U(k)、D(k)、Y(k)分别为输入量、控制量、扰动量和输出量；Gc(z)、Gm(z)分别为内模控制器和球磨机内模模型。为获得更好的鲁棒稳定性，设计滤波器F(z)=1/[1-exp(-λ)z-1]，其中λ>0，因此得到控制器Gc(z)=F(z)·Gm(z)。

2.3 仿真研究

根据给定的训练集和测试集，用LS-SVM进行广义逆系统的模型辨识。当辨识出口温度tm时，参数设置为：σ=140.1662，C=0.0645。获得的α=0.0863，b=0.5651；当辨识球磨机进出口差压时，参数设置为：σ=9.5256，C=0.0031。获得的α=0.1521，b=0.492；当辨识球磨机入口风压时，参数设置为：σ=113.7618，C=0.014。获得的α=0.0736，b=0.4274。辨识效果如图5所示。

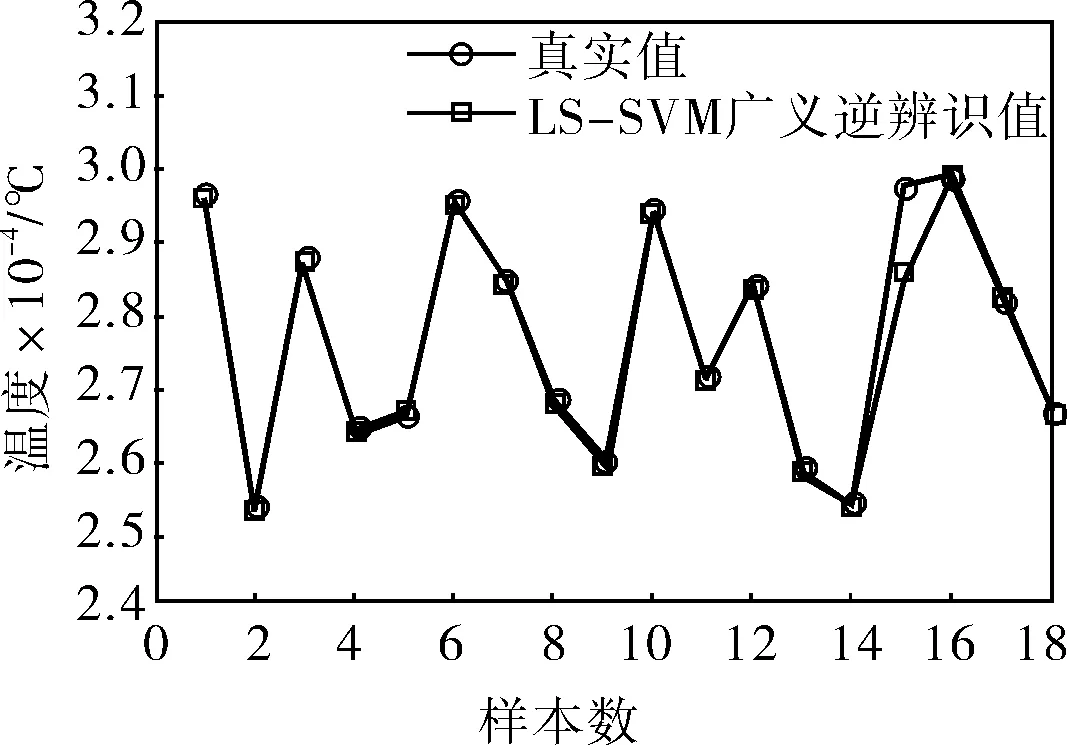
a. tm与真实值对比

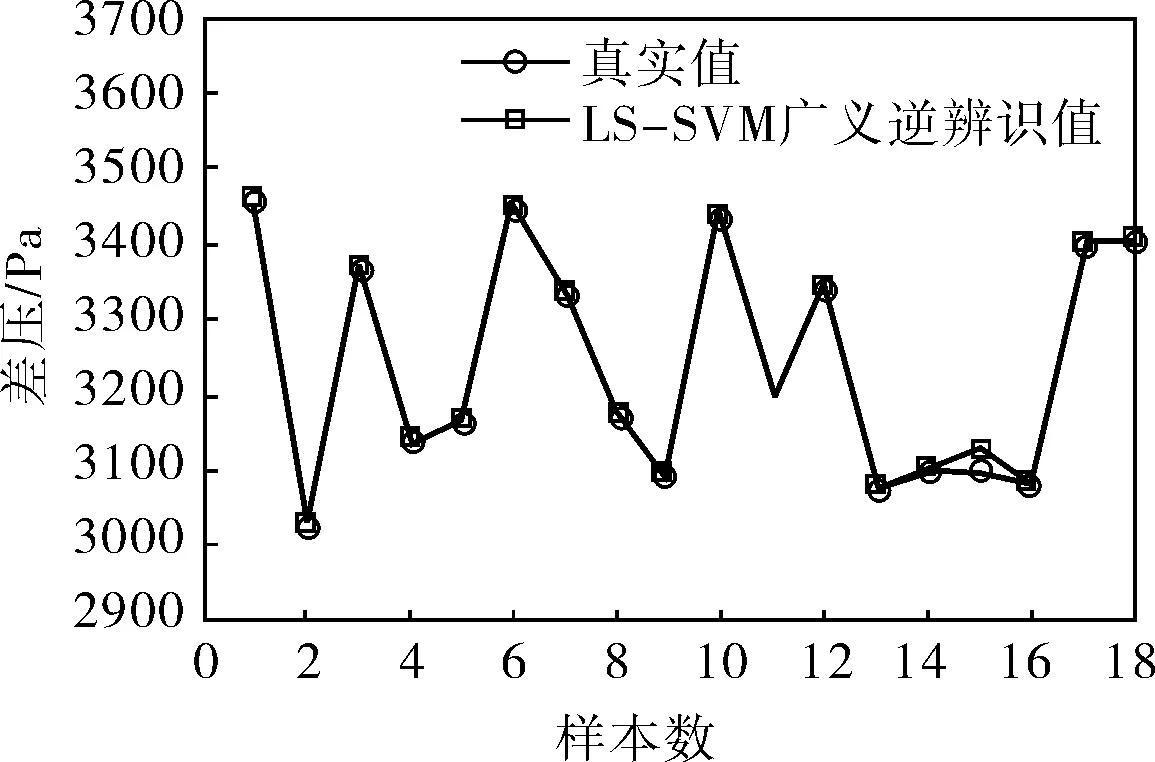
b. dp与真实值对比

c. np与真实值对比

从图5中可以看出，采用LS-SVM方法进行系统辨识具有较高的精度，可以真实反应球磨机的广义逆系统，仅仅采用小样本即可达到满意的辨识效果。对其引入内模控制，使内模控制滤波器为F(z)=a/[1-exp(-b)z-1]，其中a>0,b>0。对3个回路分别设置参数，具体参数值见表1，仿真图如图6所示。

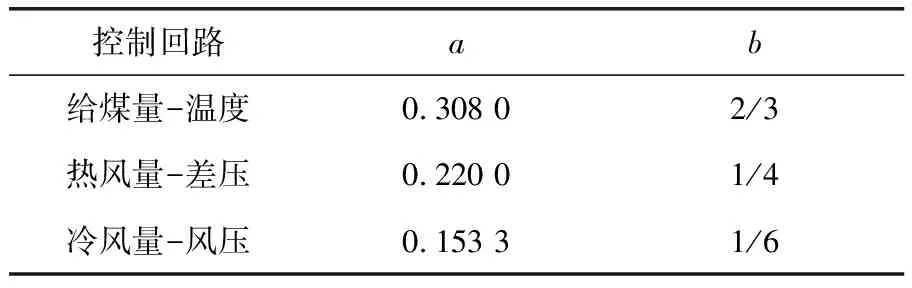
表1 内模控制滤波器参数值

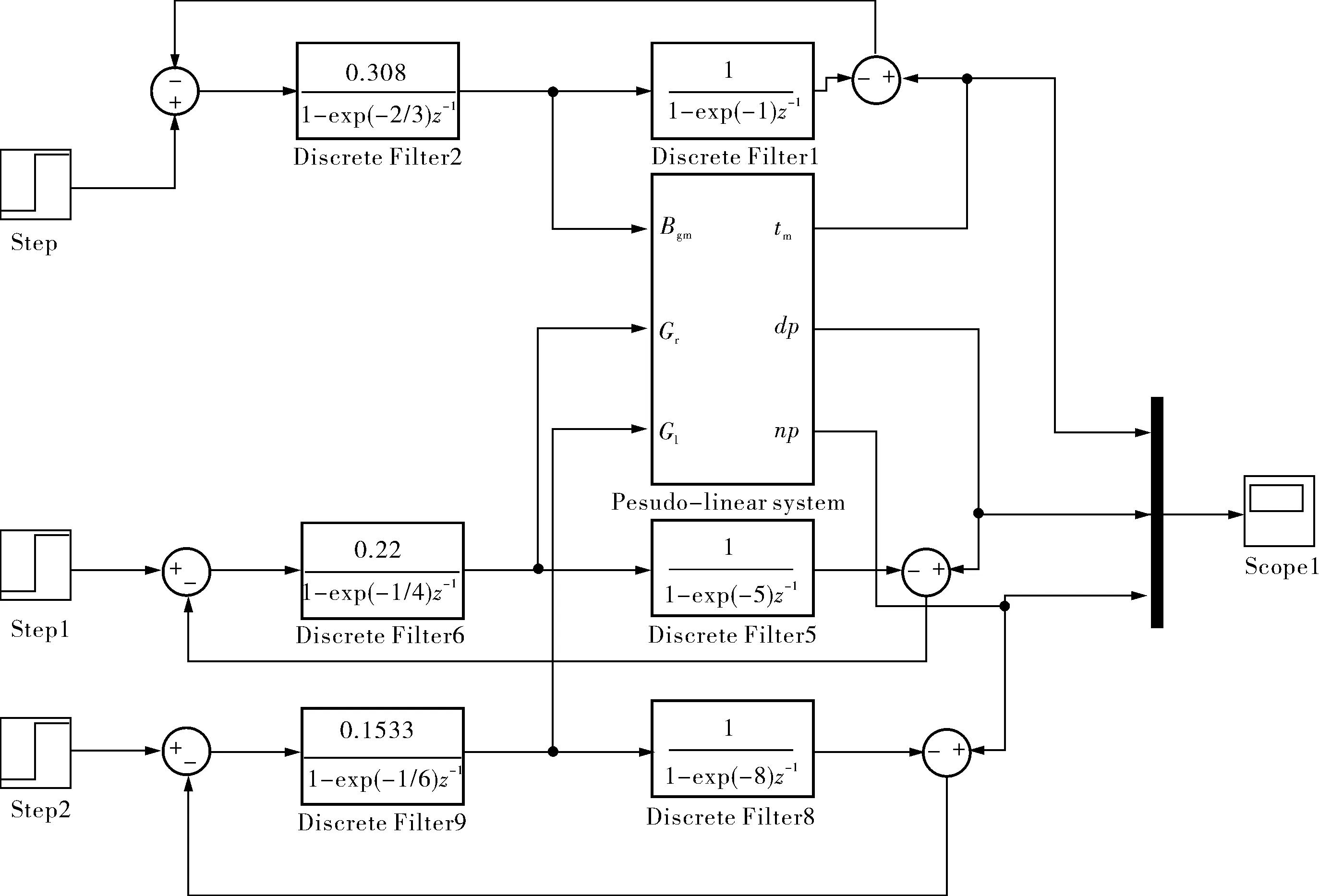
图6 LS-SVM广义逆内模控制仿真结构

笔者同时也给出了基于单回路的PID控制方法仿真对比，分别设置比例、积分和微分系数来使控制系统稳定，具体参数值见表2。采用图6的控制结构对球磨机制粉系统的出口温度tm、进出口差压dp和入口风压np分别进行控制，为使控制效果明显，控制值分别设为1℃、1Pa和1Pa，仿真对比如图7所示。

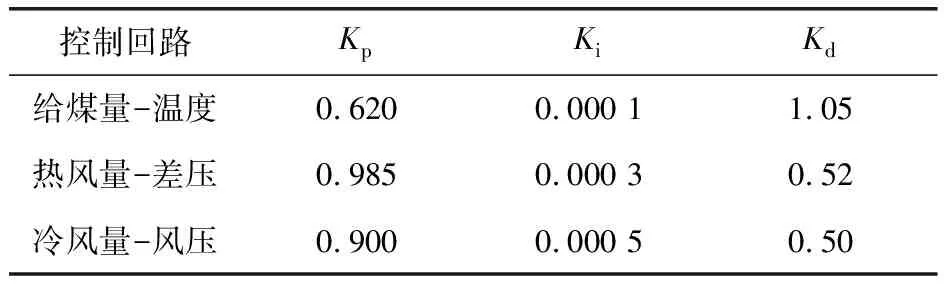
表2 基于单回路的PID控制系统参数值

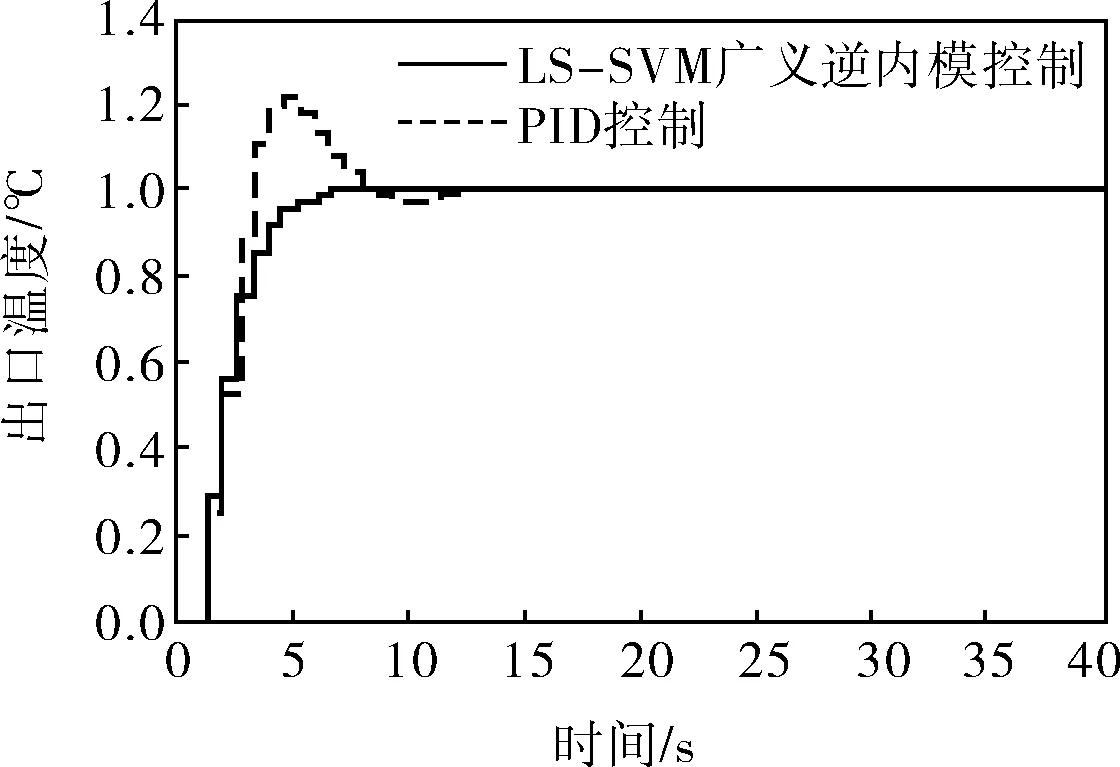
a. 对tm的输出

b. 对dp的输出

c. 对np的输出

从图7中可以明显看出，笔者采用的方法无超调，跟踪平稳性、鲁棒稳定性和准确性都优于常规PID控制方法，解耦控制效果明显，很好地解决了高阶复杂系统难以控制的问题，为多输入多输出系统的强耦合问题提供一种新的解决思路。

3 结束语

针对多变量、强耦合且难以建立精确数学模型的球磨机制粉系统，采用LS-SVM广义逆内模控制方法进行控制研究。通过采用结构风险最小化的LS-SVM建立球磨机的广义逆系统，不仅能准确逼近原系统的逆模型，而且结构简单、支持小样本训练、泛化能力强；将广义逆系统与原系统串联可得到开环伪线性系统，实现了系统的不完全解耦与近似线性化，将伪线性系统前加入内模控制形成稳定的闭环回路，其动态响应与鲁棒稳定性明显增强。经仿真表明，所采用的复合控制算法较PID控制算法具有更好的稳定性且无超调，更好地实现了多变量之间的解耦控制，为解决高阶复杂非线性系统的强耦合问题提供了一种可行的办法。