负荷模型对电力系统仿真计算的影响

邱丽萍，金小明，林勇，门锟，樊扬，李勇

（1.中国电力科学研究院，北京100192；2.中国南方电网科学研究院有限责任公司，广州510623；3.广东电网公司电网规划研究中心，广州510086）

负荷模型对电力系统仿真计算的影响

邱丽萍1，金小明2，林勇3，门锟2，樊扬3，李勇2

（1.中国电力科学研究院，北京100192；2.中国南方电网科学研究院有限责任公司，广州510623；3.广东电网公司电网规划研究中心，广州510086）

研究了负荷模型对电力系统仿真计算的影响。从暂态稳定、电压稳定等多个角度出发，结合内蒙电网等实际算例并采用BPA程序进行仿真，综合分析各种负荷模型可能对电力系统仿真结果造成的影响。结果表明，负荷模型对仿真结果的影响与负荷所处的位置、网架结构、电源分布等因素密切相关，所得结论揭示了负荷模型对电网仿真计算的重要性，有助于提高电网仿真的精度。

负荷模型；电力系统仿真；暂态稳定；电压稳定

在进行电力系统分析时，不恰当地选取负荷模型会使所得结果与系统实际情况不一致。大量仿真计算结果表明，不同的负荷模型对系统暂态稳定、电压稳定、频率稳定以及小干扰稳定的仿真计算结果有不同的影响，在临界情况下，计算结果可能会发生质的变化[1，3]。例如：美国太平洋西北系统（pacific northwest system）在电压稳定分析中，将冬季民用取暖负荷采用恒定阻抗，获得了更高的极限，节省了投资；日本东京电力系统1987年出现系统崩溃事故的原因就是在计算分析中没有充分考虑到空调负荷对无功的消耗。

1 负荷模型

在系统受到扰动时，第一、二功角摇摆周期内一般会出现电压降低的情况，特别是在振荡中心。在此期间，负荷消耗的功率大小对系统功率平衡有很大影响，从而影响功角摇摆和稳定极限[4-5]。如果实际负荷为恒电流特性，在仿真计算中采用了恒阻抗模型，负荷消耗的功率与电压的线性关系在计算中却表现为与电压成平方关系，系统扰动后电压降低，负荷吸收功率较实际降低更多。如果采用恒功率负荷模型描述实际的恒电流负荷，则会得到不同的结论。

以往研究证明系统发生较为严重故障时（电压、频率变化较为明显），采用动态模型可显著地提高仿真准确性。另外，马达对系统暂态稳定的影响与马达相对于故障点的位置、马达的负荷特性、马达的暂态特性等因素相关。

一般情况下，功角的第一摆稳定取决于2个因素：①短路期间发电机获得的加速、减速能量；②短路故障消失后加速、减速能量的释放。

以单机－无穷大系统（见图1）为例来分析负荷模型对这2个因素的影响。算例采用3种负荷模型：①东北大扰动实验推荐的考虑配电网络的综合负荷模型，简称综合负荷模型。综合负荷模型参数为：配电系统网络阻抗j0.06 p.u.，马达比例60%，负载率40%，马达参数见表1；静态负荷比例40%；静态负荷构成为30%恒阻抗+30%恒电流+ 40%恒功率；静态负荷功率因数cos φ为0.85；②50%Ⅲ型马达+50%恒阻抗模型，马达负载率50%，参数见表1；③静态30%恒阻抗+40%恒电流+30%恒功率模型，简称静态3-4-3 ZIP模型。

图1 单机－无穷大系统Fig.1Single-machine and infinite bus power system

表1 模型的马达参数Tab.1Parameters of motor model p.u.

表1中：Rs为马达定子电阻；Xs为马达定子电抗；Xm为马达激磁电抗；Rr为马达转子电阻；Xr为马达转子电抗；Tj为马达的惯性时间常数。

2 负荷模型对暂态稳定的影响

2.1 负荷模型对送端加速能量的影响

功率从发电机侧流向无穷大系统侧，分析负荷模型对送端机组短路期间获得的加速能量的影响。在0 s时线路1母线2侧发生三相短路故障，0.12 s时开关动作断开线路1。负荷吸收的有功见图2，在短路期间综合负荷模型吸收有功最大，50%Ⅲ马达＋50%恒阻抗模型其次，静态3－4－3 ZIP模型吸收有功最小。系统电压方面，动态负荷将在短路期间向系统提供容性无功，而静态负荷吸收无功接近于0，短路期间系统电压由高到低依次对应综合负荷模型、50%Ⅲ型马达+50%恒阻抗模型、静态负荷模型，系统电压越高越有利于发电机功率外送。

综合上述两方面的影响，采用综合负荷模型时发电机的电磁功率最大而加速功率最小，发电机在短路期间获得的加速能量最小，采用静态负荷模型时发电机的加速功率最大，发电机获得的加速能量最大，50%III型马达+50%恒阻抗模型在短路期间获得的加速能量居中，如图4所示。

图2 短路期间有功负荷Fig.2Active power during short circuit

图3 短路期间母线1电压Fig.3Voltage of bus 1 during short circuit

图4 短路期间发电机加速功率Fig.4Acceleration power of generator during short circuit

2.2 负荷模型对受端减速能量的影响

功率从无穷大系统侧流向发电机侧，分析负荷模型对受端机组短路期间减速功率的影响。在0 s时线路1母线2侧发生三相短路故障，0.1 s时开关动作断开线路1。短路期间负荷功率、系统电压以及发电机减速功率见图5～图7。

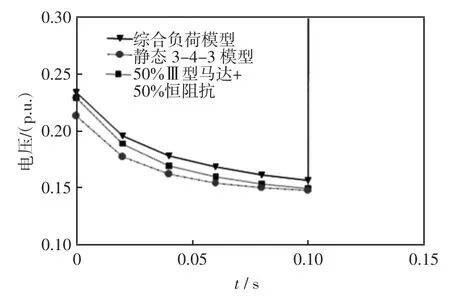
图5 短路期间母线1电压Fig.5Voltage of bus 1 during short circuit

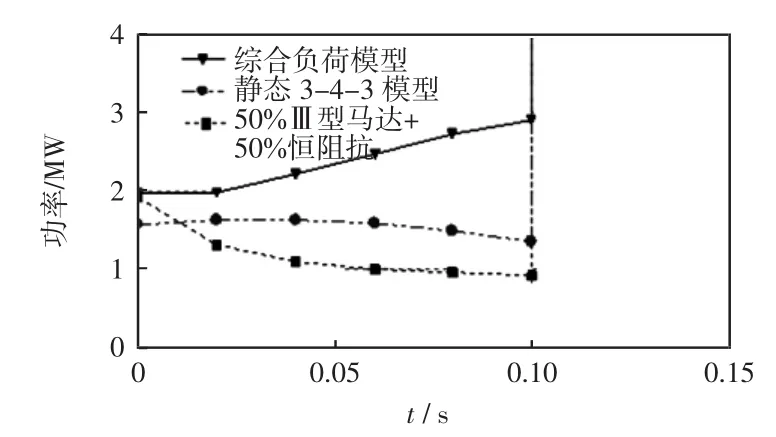
图6 短路期间负荷有功功率Fig.6Active power during short circuit

图7 短路期间发电机减速功率Fig.7Braking power of generator during short circuit

短路期间系统电压按由高到低的顺序依次为综合负荷模型、50%Ⅲ型马达+50%恒阻抗模型、静态负荷模型，负荷有功功率按由大到小的顺序也是综合负荷模型、50%Ⅲ型马达+50%恒阻抗、静态负荷模型，因此故障期间发电机减速功率由大到小的顺序是综合负荷模型、50%Ⅲ型马达+50%恒阻抗、静态负荷模型。

造成以上结果的主要原因是：故障后恢复阶段马达电磁转矩减小、逐渐减速、滑差拉大，随着滑差在短时间内的迅速增大，马达将从系统内吸收额外功率，其后功率保持在较高的水平，在故障前的功率附近摇摆。对受端而言，故障后恒阻抗负荷吸收的有功功率随电压降低而减小，意味着受端机组的有功不平衡量减少，有利于系统功率平衡；而马达负荷在故障后的增大，意味着受端机组的有功不平衡量增加，不利于系统功率平衡。对送端而言，马达负荷和恒阻抗负荷对系统稳定性的影响与处于送端时的影响刚好相反。

3 负荷模型对电压稳定的影响

电压稳定计算与电力系统其他的定量计算比较，对负荷模型的依赖程度更强。负荷模型是电压失稳过程中最活跃、最关键的因素[6-8]。

以内蒙古阿拉善受端电网为实际算例，分析受端电网负荷模型对电压稳定的影响。阿拉善地区仅通过吉兰太500 kV主变与主网相连，其接线见图8。阿拉善地区为典型的受端电网，当其主要供电电源线路吉兰太-乌海线故障时，末端负荷站存在电压稳定问题。

图8 阿拉善地区接线Fig.8Network of Alashan

阿拉善电网分别采用60%Ⅲ型马达+40%恒阻抗、100%恒阻抗、100%恒电流、100%恒功率、100%Ⅲ型马达、东北大扰动实验推荐的考虑配电网络的综合负荷模型（简称综合负荷模型）。故障点选择在吉兰太-乌海线乌海侧，故障形式为三永故障，马达模型为Ⅲ型。阿拉善地区的受电极限如表2所示。

阿拉善地区受电为171 MW，分别采用6种负荷模型时额济纳站的220 kV母线电压如图9所示。可以看出，采用静态模型时电压恢复较快，不存在电压稳定问题；采用100%马达和综合负荷模型时，故障后电压无法恢复，直至出现电压崩溃；采用的60%Ⅲ型马达+40%恒阻抗模型时，故障后电压恢复较慢，持续低于0.75 p.u.的时间超过1 s。故障后电压恢复水平由高到低的顺序依次为恒阻抗模型、恒电流模型、恒功率模型、60%Ⅲ型马达+ 40%恒阻抗模型、综合负荷模型和100%马达。总之，受端系统电压稳定水平随受端电网马达比例的增加而下降。

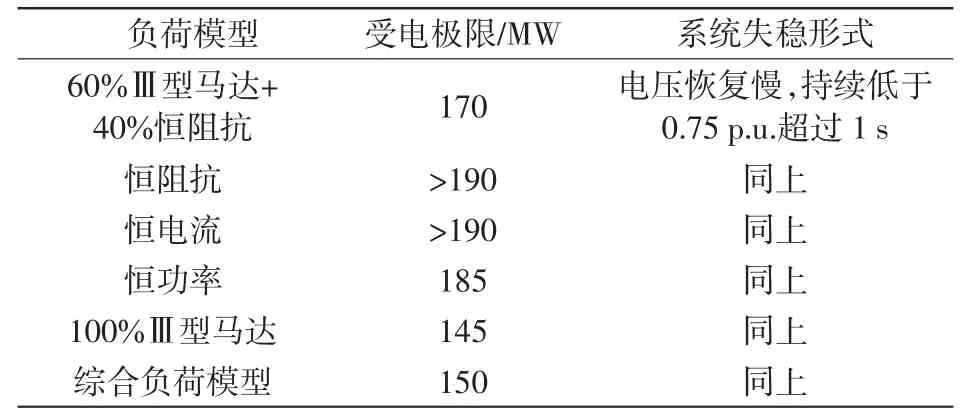
表2 阿拉善地区受电极限Tab.2Maximum receiving power of Alashan network

图9 额济纳220 kV母线电压曲线Fig.9Voltage of Ejina station bus

（1）马达负荷对电压稳定性的影响。马达的有功、无功功率与滑差间的关系为

式中：P、Q分别为马达吸收的有功和无功功率；Pmax为一定电压水平下马达可吸收的最大有功功率；s为马达滑差；scr为马达临界滑差。

故障恢复阶段马达电磁转矩减小，而马达的机械功率还保持在较高的水平，造成马达逐渐减速，滑差拉大，随着滑差在短时间内的迅速增大，马达将从系统内吸收大量无功。如果马达能恢复稳定，滑差减小，吸收的有功和无功将逐渐减小到稳态前的水平。如果电压降低较多（低于0.4 p.u.）导致许多马达难以恢复，马达滑差增大，吸收无功功率增大，引起系统电压的进一步降低，造成受端电网电压崩溃，系统电压失稳。

（2）静态模型对电压稳定性的影响。静态负荷吸收的功率主要受电压变化影响，静态负荷在故障后不会像马达负荷那样吸收更多的无功。恒阻抗、恒电流负荷吸收的无功功率还会在故障后的恢复期间随着系统电压的下降而下降，在一定程度上缓解受端系统的无功缺额，有利于系统电压的恢复。

4 结论

（1）负荷模型在电压能够快速恢复的情况下对稳定计算结果影响很小。

（2）负荷模型无功电压效应越明显，如恒阻抗模型，会促进电压的恢复，有利于电网稳定性。

（3）故障后送端机组加速、受端机组减速，送端负荷模型电压效应低会提高稳定性，受端相反。

[1]Sekine Y，Ohtsuki H.Cascaded voltage collapse[J].IEEE Trans on Power Systems，1990，5（1）：250-256.

[2]Popovic D，Hiskens I A，Hill D J.Investigations of loadtap changer interaction[J].International Journal of Electrical Power&Energy Systems，1996，18（2）：81-97.

[3]Pal M K.Assessment of corrective measures for voltage stability considering loads dynamics[J].International Journal of Electrical Power&Energy Systems，1995，17（5）：325-334.

[4]汤涌，张红斌，侯俊贤，等（Tang Yong，Zhang Hongbin，Hou Junxian，et al）.负荷建模的基本原则和方法（Study on essential principle and methods for load modeling）[J].电网技术（Power System Technology），2007，31（4）：1-5.

[5]张红斌，汤涌，张东霞，等（Zhang Hongbin，Tang Yong，Zhang Dongxia，et al）.负荷建模技术的研究现状与未来发展方向（Present situation and prospect of load modeling technique）[J].电网技术（PowerSystemTechnology），2007，31（4）：6-10.

[6]EL-Hawary M E，Dias L G.Incorporation of load models in load-flow studies：form of model effects[J].IEEE Proceedings C，1987，134（1）：27-30.

[7]Vaahedi Ebrahim.Dynamic load modeling in large scale stability studies[J].IEEE Trans on Power Systems，1988，3（3）：1039-1045.

[8]赵勇（Zhao Yong）.感应电动机负荷模型的静态特性分析（Analysis of static characteristics of induction motor models）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（2）：86-92.

Impact of Load Model on Power System Simulation

QIU Li-ping1，JIN Xiao-ming2，LIN Yong3，MEN Kun2，FAN Yang3，LI Yong2
（1.China Electric Power Research Institute，Beijing 100192，China；2.China Southern Power Grid Science Reserch Institute Co.，Ltd.，Guangzhou 510623，China；3.Grid Planning and Research Center of Guangdong Power Grid Corporation，Guangzhou 510086，China）

This paper studies the influence of load model on power system simulation is investigated in this paper.For the sake of the transient stability，voltage stability，etc.the practical example of Inner Mongolia power grid is simulated by BPA，and the influence of various load models on power system simulation result is studied.On the basis of practical examples，it can be asserted that the effect of load modeling is closely related to the place，structure of power grid and power distribution.The results indicate that the importance of load models for power system simulation，which is beneficial to enhance the power system simulation accuracy.

load model；power system simulation；transient stability；voltage stability

TM711

A

1003-8930（2014）11-0087-04

邱丽萍（1979—），女，硕士，工程师，研究方向为电力系统分析与控制等。Email：qiulp@epri.sgcc.com.cn

2012-08-18；

2012-12-29

金小明（1963—），男，教授级高级工程师，研究方向为电力系统规划与直流输电技术。Email：jinxm@csg.cn

林勇（1973—），男，硕士，高级工程师，研究方向为电力系统规划。Email：linyong@csg.cn