捕食者具有性别结构及时滞的母系社会捕食模型
2014-08-02吴兰琦魏凤英
吴兰琦,魏凤英
(福州大学数学与计算机科学学院,福建 福州 350116)
捕食者具有性别结构及时滞的母系社会捕食模型
吴兰琦,魏凤英
(福州大学数学与计算机科学学院,福建 福州 350116)
研究了捕食者具有性别结构及时滞的母系社会捕食模型.通过计算雅克比矩阵的特征值得到了系统正平衡点局部稳定性的充分条件,当时滞τ穿过τ0时,系统在正平衡点附近产生Hopf分支及周期解.运用迭代法得出正平衡点全局渐近稳定的条件;运用隐函数存在定理,分析了捕食者的出生率对各个种群密度的影响,并研究了雌性捕食者死亡率对雌性捕食者幼崽出生率的影响.举例说明了所得结果的有效性.
性别结构;时滞;全局渐近稳定;Hopf分支
1 预备知识
在自然界中,一般的动物种群具有雌雄之分,而且雌性和雄性种群表现出不同的生理特征和分工.因此,在研究种群动力学模型时,时滞或控制参数对微分方程解的拓扑结构会产生较大的影响[1-8].在很多情况下,时滞或控制参数的改变会破坏正平衡点的稳定性而产生Hopf分支.所以,在研究种群的相互作用时,考虑性别结构和时滞的影响更具有实际意义.
近年来,许多学者对具有性别结构的种群动力学模型进行了研究.大部分学者考虑食饵具有性别结构的模型[9-11],例如,刘汉武等人研究了如下模型[7]:
(1)
其中:m(t)和f(t)分别为雄性食饵和雌性食饵在时刻t的种群密度,x(t)为捕食者在时刻t的种群密度;d1和d2分别为雄性食饵和雌性食饵的瞬时死亡率;b1和b2分别为雄性幼崽和雌性幼崽的出生率;记β=b2-d2;k为食饵种群的种内竞争率;假设雌性个体不会因为没有配偶而不能生育.文献[9]通过特征方程分析了平衡点的局部稳定性的条件,以及性别偏食对正平衡点稳定性和性别比变化的影响.
对于捕食者具有性别结构的模型的研究目前仍然比较少,而捕食者具有阶段结构的模型则得到许多学者的研究[3-6,12-13].特别是王稳地,陈兰荪研究了一类捕食者具有阶段结构的时滞系统[3]
(2)
其中:xi(t),xm(t),y(t)分别代表幼年捕食者、成年捕食者、食饵在t时刻的密度;Ω代表幼年捕食者到成年捕食者的转化率;τ2为捕食者由于怀孕而产生的孕期时滞.文献[3]给出的系统为永久持续生存的系统,且其给出了正平衡点为全局渐近稳定的充分条件,证明了模型存在轨道渐近稳定的周期解.
自然界中存在着一些生存在母系社会的生物种群,如蚂蚁、蜜蜂、狮子等,其中雌性负责捕猎和生育后代,雄性负责交配和争夺地盘,除非遇到强大的对手或食物极度紧缺,一般雄性不参与捕猎,因此,雌性在母系社会种群中的地位是很高的.本文研究的是一类捕食者具有性别结构及时滞的母系社会捕食模型
(3)
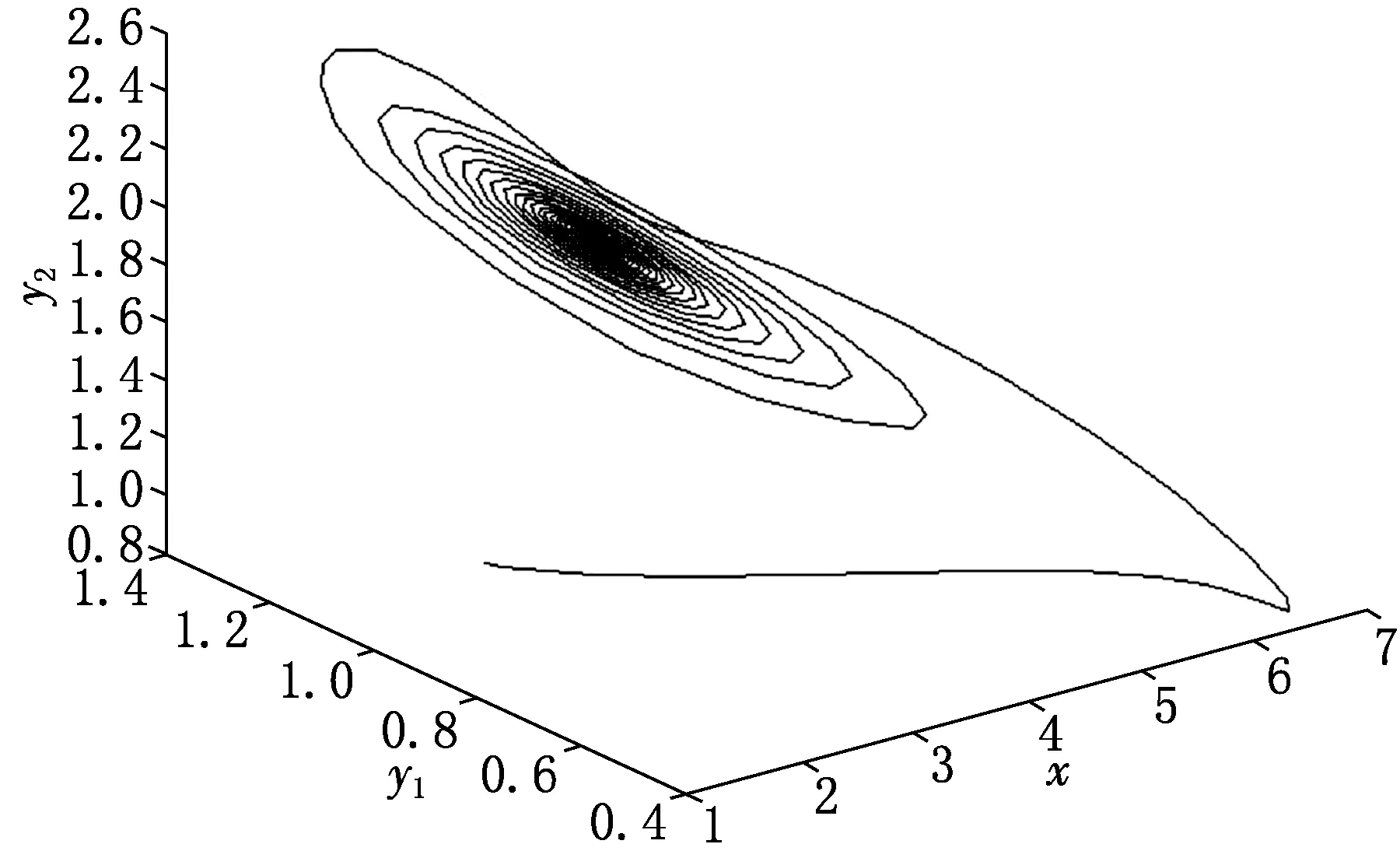
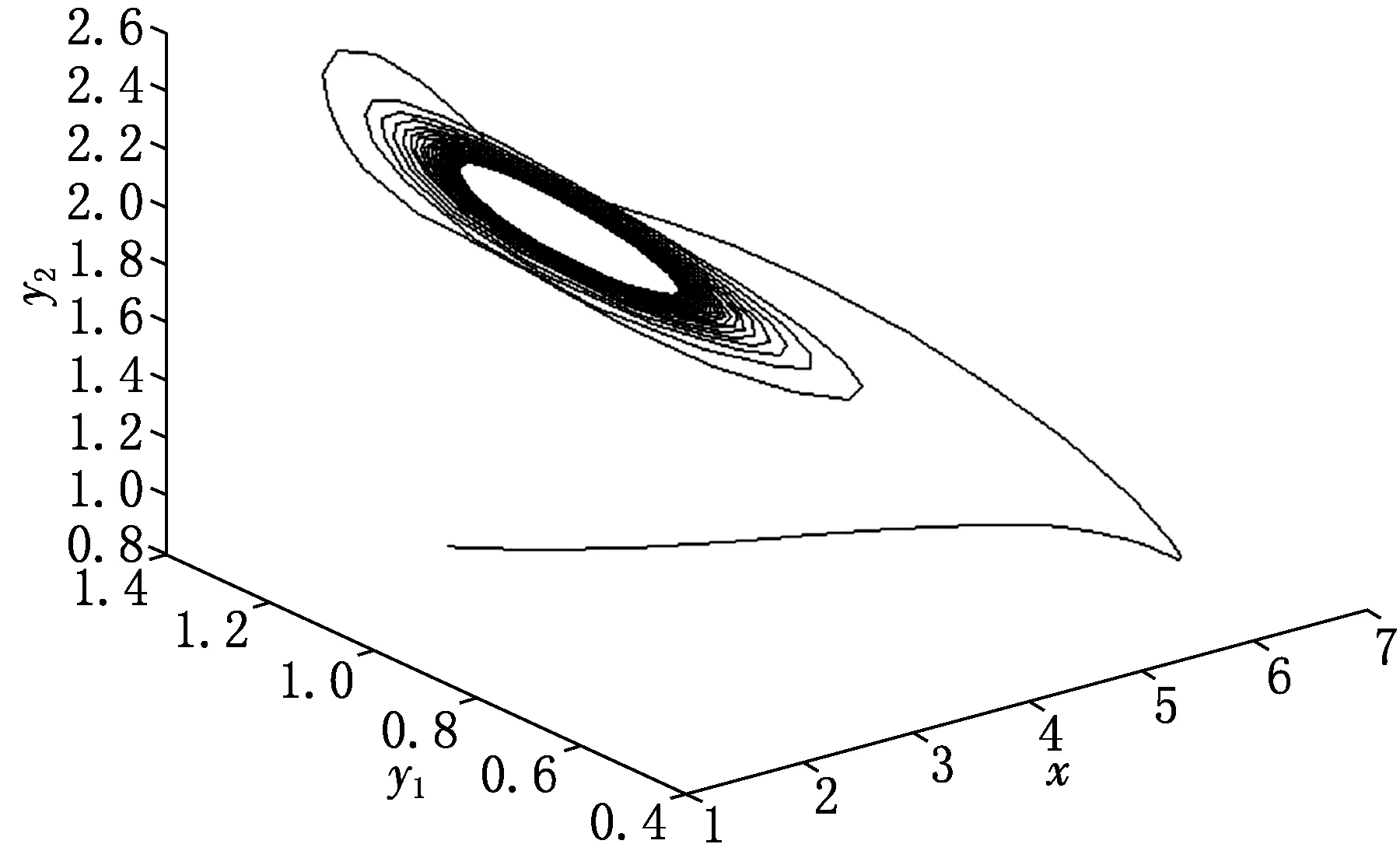
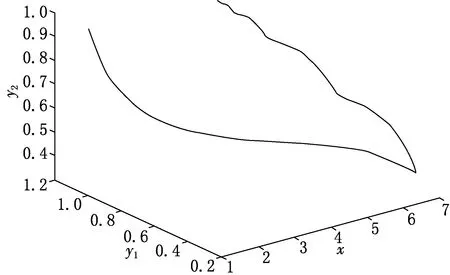
其中:r为食饵的内禀增长率;b1/b表示营养转化率且b1 其中 (4) 特征方程(4)在E0(0,0,0)简化为 (r-λ)(-c1-λ)(-c2-λ)=0, (5) 其中:λ1=r,λ2=-c1,λ3=-c2.所以E0不稳定. 特征方程(4)在E1简化为 (6) 特征方程(4)在E*简化为 (7) 其中λ1=-c1,(7)式的其他根由 决定,上式可化为 P(λ)+e-λτQ(λ)=0. (8) 情形1 当τ=0时,(8)式可以化为 λ2+(P1+Q1)λ+P0+Q0=0. (9) 其中: 所以,正平衡点E*必然局部渐近稳定. 情形2 当τ>0时,设λ=iω(ω>0)是(8)式的一个根当且仅当(8)式满足 P(iω)+e-iωτQ(iω)=0. (10) 分离(10)式的实部和虚部,得到 ω2-P0=Q1ωsinωτ+Q0cosωτ,P1ω=Q0sinωτ-Q1ωcosωτ. (11) 即 (12) 由sin2ωτ+cos2ωτ=1,对(12)式两边同时平方并相加,得到 (13) 则当τ=τn时,±iω0是(8)式的一对纯虚根.从而,正平衡点在τ∈[0,τ0)时局部渐近稳定. 在(8)式中,λ关于τ求导易得 其中: M=P1+Q1cosω0τ,N=2ω0-Q1sinω0τ, 因此,得到下面结论. 定理2.1 (ⅰ)E0不稳定. (ⅱ) 当k2b1r-ac2>0时,E1不稳定;当k2b1r-ac2<0时,E1局部渐近稳定. (ⅲ) 在k2b1r-ac2>0的条件下,若P0-Q0>0成立,则对所有的τ≥0,正平衡点E*局部渐近稳定.若P0-Q0<0成立,正平衡点E*在τ∈[0,τ0)时局部渐近稳定,并且正平衡点在τ=τ0处产生Hopf分支;当τ>τ0时,系统(3)在正平衡点E*处存在周期解. 定理3.1 若k2b1r-ac2>0,k2b1b-ad<0,则平衡点E*全局渐近稳定. (14) (15) (16) (17) (18) (19) (20) (21) (22) 令(22)式中的n→+∞,得到 内部平衡点E*满足: (23) 定义: 则(23)式表达为 于是 综上所述,(Ⅰ),(Ⅲ),(Ⅴ)说明:若雄性幼崽出生率k1增大,则雄性捕食者y1的平衡密度增大,而雄性捕食者一般不捕获食饵,所以食饵x的平衡密度不会随之变化;又由于系统假设没有雄性,雌性捕食者也能繁殖后代,所以雌性捕食者y2的平衡密度不因雄性捕食者种群密度的变化而变化. (Ⅱ),(Ⅵ)说明:若雌性幼崽出生率k2增大,则雌性捕食者y2的平衡密度增大,这加强了雌性捕食者对食饵的捕获,所以食饵x的平衡密度减小. 由定理3.1,当P0-Q0>0时,正平衡点E*局部渐近稳定,且 在遗传学上,后代的性别比例为随机分配的.而在自然界中,动物通过控制自己后代的性别,来维持种群的稳定.在母系社会中,当雌性受疾病、环境资源等因素影响导致死亡率较高时,雌性会生产更多的雌性后代,以保证种群的稳定.这表现为雌性幼儿的出生率随着死亡率的增大呈现整体上升趋势. 考虑以下系统: (24) 图1 当τ=6<7.175 3=τ0时,E*(2,1,2)局部渐近稳定 图2 当τ=8>7.175 3=τ0时,E*(2,1,2)不稳定 图3 当τ≥0时,E*(5.36,1.179 2,0.88)全局渐近稳定 本文探讨了一类捕食者具有性别结构及时滞的母系社会捕食模型,通过雅克比矩阵的特征值以及儒歇定理,得到了系统正平衡点局部稳定性的充分条件,当时滞τ穿过τ0时,系统在正平衡点附近产生Hopf分支及周期解;运用迭代法,我们得到正平衡点全局渐近稳定的条件;通过数值模拟,充分验证所得结果的有效性. 运用隐函数存在定理,我们分析了捕食者的出生率对各个种群密度的影响,并发现当雄性幼崽出生率k1增大时,雄性捕食者y1的平衡密度随之增大,而食饵x和雌性捕食者y2的平衡密度不会随之变化,当雌性幼崽出生率k2增大,雌性捕食者y2的平衡密度随之增大,食饵x的平衡密度反而减小. 文中运用函数和极限的思想,通过固定c2以外的系数,研究了雌性捕食者死亡率c2对雌性捕食者幼崽出生率k2的影响,研究发现:当雌性的死亡率升高到足够大时,雌性幼儿的出生率随着死亡率的增大呈现整体上升趋势.这一结论证实了这样一个生物学观点:在部分母系社会生物种群中,当雌性受疾病、环境资源等因素影响导致死亡率较高时,雌性会生产更多的雌性后代,以保证种群的稳定. [1] 杨斌,王静.具有Holling Ⅳ型功能性反应的非自治三种群食物链模型的周期解[J].东北师大学报:自然科学版,2012,44(1):10-15. [2] 吕堂红,周林华.具时滞物价瑞利方程的Hopf及共振余维2分支[J].东北师大学报:自然科学版,2012,44(4):43-47. [3] WANG WEN-DI,CHEN LAN-SUN.A predator-prey system with stage structure for predator[J].Applied Mathematics and Computation,1997,33(8):83-91. [4] SAPNA DEVI.Effects of prey refuge on a ratio-dependent predator-prey model with stage-structure of prey population[J].Applied Mathematical Modelling,2013,37(6):4337-4349. [5] HU HAI-JUN,HUANG LI-HONG.Stability and Hopf bifurcation in a delayed predator-prey system with stage structure for prey[J].Nonlinear Analysis:Real World Applications,2010,11(4):2757-2769. [6] LI FENG,LI HONG-WEI.Hopf bifurcation of a predator-prey model with time delay and stage structure for the prey[J].Mathematical and Computer Modelling,2012,55(3/4):672-679. [7] 于新艳,王静.污染环境下具有Beddington-DeAngelis功能性反应的捕食者-食饵系统的动力学行为[J].东北师大学报:自然科学版,2013,45(1):6-12. [8] 郝丽杰,蒋贵荣,鹿鹏.具有垂直传染和脉冲接种的SIRS传染病模型的周期解[J].东北师大学报:自然科学版,2013,45(3):35-40. [9] 刘汉武,王荣欣,刘建新.具有性别结构的食饵捕食者模型[J].生物数学学报,2005,20(2):179-182. [10] 王波,张建勋.具性别偏食和Holling Ⅱ类功能反应的三种群系统的研究[J].宁波大学学报,2012,25(3):38-41. [11] 李学鹏,杨文生.一类具有性别结构的捕食系统[J].厦门理工学院学报,2007,15(4):50-54. [12] KUNAL CHAKRABORTYA,MILON CHAKRABORTYB,T K KAR.Optimal control of harvest and bifurcation of a prey-predator model with stage structure[J].Applied Mathematics and Computation,2011,217(21):8778-8792. [13] CHENFENG-DE,WANG HAI-NA,LIN YU-HUA,et al.Global stability of a stage-structured predator-prey system[J].Applied Mathematics and Computation,2012,223(15):45-53. (责任编辑:陶 理) Maternal society predator-prey model with time delay and sex structure to predator WU Lan-qi,WEI Feng-ying (College of Mathematics and Computer Science,Fuzhou University,Fujian 350116,China) A kind of predator-prey model in maternal society with time delay and sex structure to predator is investigated in this paper.By analyzing the eigenvalues of Jacobian matrices,the sufficient conditions of the local stability of the positive equilibrium are obtained,when the delayτcrosses some critical valueτ0,Hopf bifurcations and periodic solutions occur at the positive equilibrium of the system.Furthermore,by the iterative method,the conditions of global stability for the positive equilibrium are discussed.By the theorem of the existence of implicit function,the influence of the birth rates on densities of species is analyzed,moreover,the effect of the death rate of female predator with respect to the birth rate of female predator is investigated.Finally,numerical simulations are carried out to illustrate our main results. sex structure;time delay;globally asymptotical stability;Hopf bifurcation 1000-1832(2014)04-0022-08 10.11672/dbsdzk2014-04-004 2013-10-04 国家自然科学基金资助项目(11201075);福建省自然科学基金资助项目(2010J01005). 吴兰琦(1990—),女,硕士研究生;通讯作者:魏凤英(1976- ),女,博士,教授,主要从事生物数学与随机微分方程研究. O 175.14 [学科代码] 110·44 A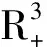
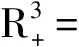
2 局部渐近稳定和Hopf分支
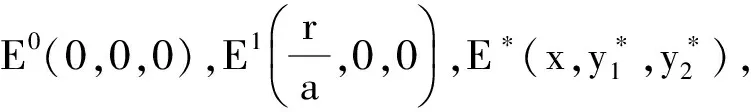
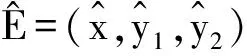
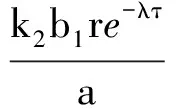
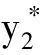
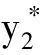
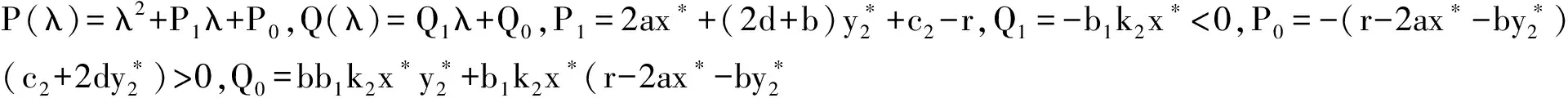
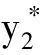
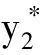
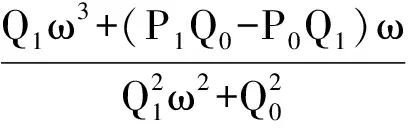
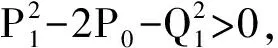
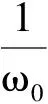

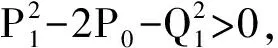
3 正平衡点的全局稳定性

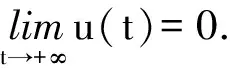
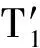
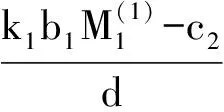
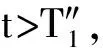
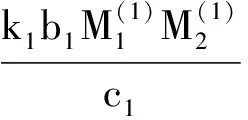
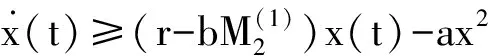
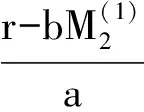
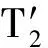
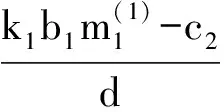
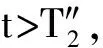
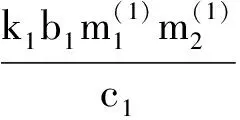
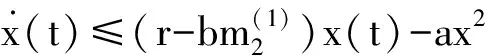
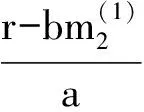

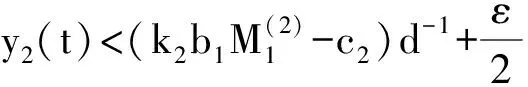
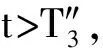
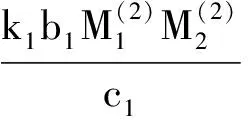
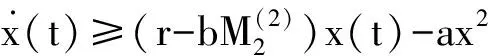

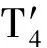
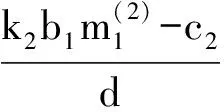
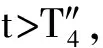
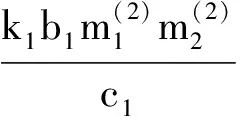
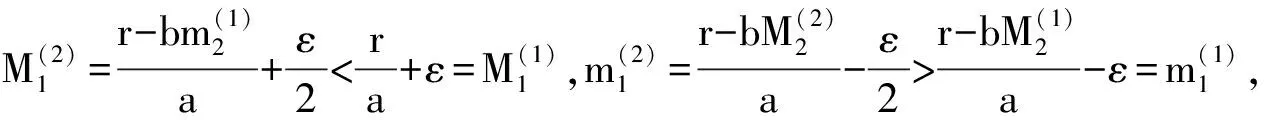
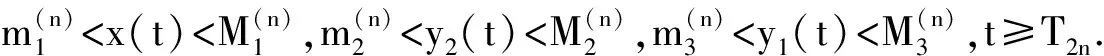
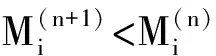

4 两性幼崽出生率对平衡密度的作用
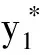
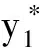
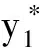
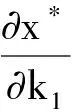
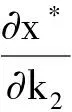
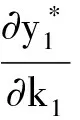
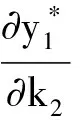
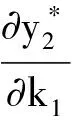
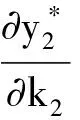
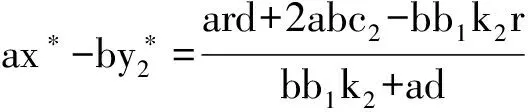
5 死亡率对出生率的影响
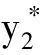
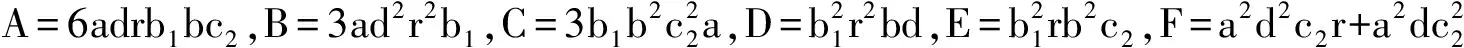
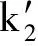
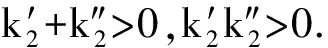
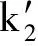
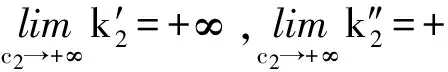
6 数值模拟
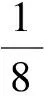
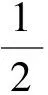
7 结论
