在黎曼流形上满足Schur定理的一个半对称射影共形联络
2014-08-02许达允全哲勇金光植
许达允,全哲勇,金光植
(1.金日成综合大学 数学系,朝鲜民主主义人民共和国 平壤;2.延边大学理学院 数学系, 吉林 延吉 133002)
A.Fridman等在文献[1]中首次提出了半对称度量联络的概念,其后H.A.Hayden[2]和K.Yano[3]分别提出和研究了黎曼流形上半对称度量联络概念和性质.随着对半对称度量联络研究的不断深入,N.S.Agache等又提出了多种类型的半对称联络[4],在此基础上,文献[5-8]分别讨论了射影等效Levi-Civita联络的半对称联络性、射影共形联络等内容.随后,文献[9]给出了度量联络和非度量联络的常曲率条件,文献[10-11]在提出半对称非度量联络的物理模型的基础上,讨论了半对称非度量联络的相互联络应用于古典重力场和电磁场的统一理论.基于以上研究,本文首先定义了黎曼流体上的一个半对称射影共形联络,且指出这种联络在特殊情形下可成为几个联络,即:半对称射影联络、半对称共形联络、对称射影共形联络、射影联络、共形联络以及Levi-Civita联络,并给出了半对称射影共形联络的常曲率条件和此联络的相互联络常曲率条件.
1 半对称射影共形联络
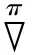
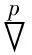
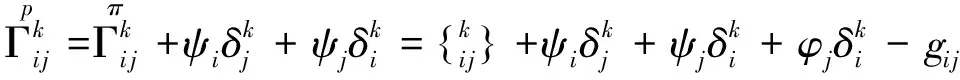
(1)
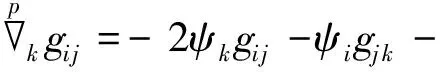
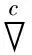
定义3联络称为半对称射影共形联络,如果在黎曼流体(M,g)里联络是射影等效于半对称度量联络和共形等效.
如果σi=0,则半对称射影共形联络是半对称射影联络; 如果ψi=0,则半对称射影共形联络是半对称射影联络; 如果φi=0,则半对称射影共形联络是对称射影共形联络.对称射影共形联络满足,, 该联络系数为σk.
注1如果σk=ψk=0,则; 如果σk=φk=0,则半对称射影共形联络是射影联络;如果ψk=φk=0,则是共形联络(与Levi-Civita联络共形等效);如果φi=σi=ψi=0,则
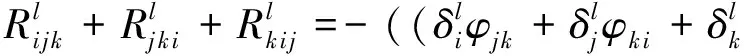
(2)
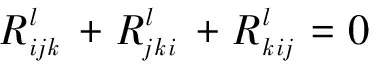
(3)
其中φi j=iφj-jφi.
2 半对称射影共形联络的常曲率条件
如果在黎曼流体的任何点P上的截面曲率与二维子空间的选择无关,则曲率张量可表示为Ri j kl=K(P)(gilgjk-gikgjl),如果k是常数,则联络有常曲率.
定理1在连接的黎曼流体(M,g)(dimM≥3)里半对称射影共形联络有常曲率的必要且充分条件是
2σh-ψh-φh=0.
(4)
证明如果黎曼流体(M,g)里半对称射影共形联络的截面曲率与二维子空间的选择无关,则曲率张量为,把该式代入到(3)式中得
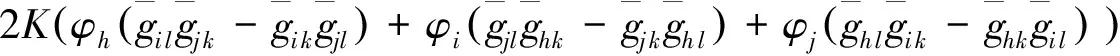
(5)
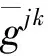
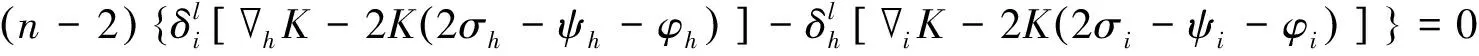
通过对指标i,l实施化简得(n-1)(n-2)[hK+2K(2σh-ψh-φh)]=0.这表明,在M≥3的情况下,K为常数的必要且充分的条件是(4)式成立.
由定理1可给出在连接的黎曼流形(M,g)(dimM≥3)中满足Schur定理的半对称射影共形联络的5个类型:
1)σi=0 (,ψh=-φh)时,
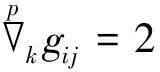
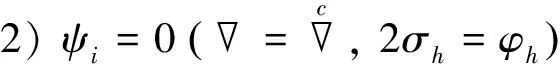

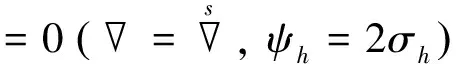
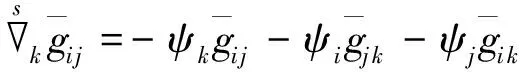
或
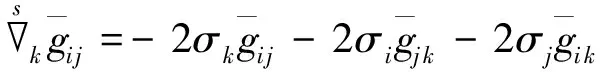
4)ψ=σ=π时,


或

(6)
注2从(4)式可知:如果ψh=σh=0,则φh=0;如果σh=φh=0,则ψh=0;如果φh=ψh=0,则σh=0.但如果σh=ψh=φh=0,则,这时Schur定理成立.
所以在σh=ψh=0,φh≠0的半对称度量联络或在σh=φh=0,ψh≠0的射影对称联络的情形下Schur定理不成立,而且在φh=ψh=0,σh≠0的共形对称联络的情形下Schur定理仍然不成立.
3 半对称射影共形联络的相互联络
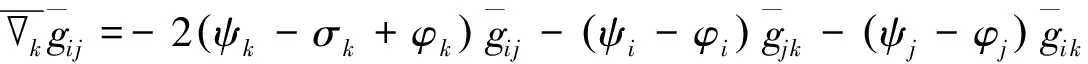
(7)



(8)
定理2在连接的黎曼流体(M,g)(dimM≥3)中,半对称射影共形联络的相互联络有常曲率的必要且充分条件是
ψh+2φh-2σh=0.
(9)

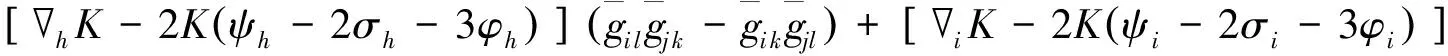

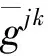
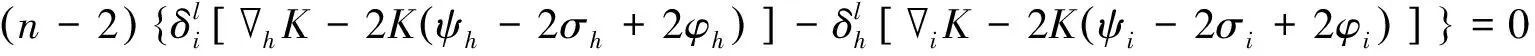
通过对指标i,l实施化简得(n-1)(n-2)[hK-2K(ψh-2σh+2φh)]=0.这表明,在dimM≥3,K为常数的情形下,k是常数的必要且充分的条件为(9)式成立.
由定理2可给出在连接的黎曼流形(M,g)(dimM≥3)上满足Schur定理的半对称射影共形联络的如下4个特殊类型:
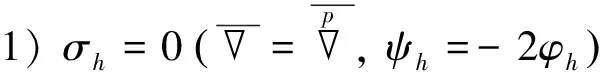
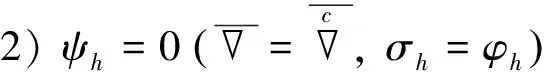
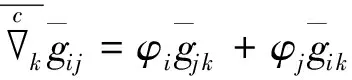
(10)

(11)
4)ψh=2σh-2φh时,
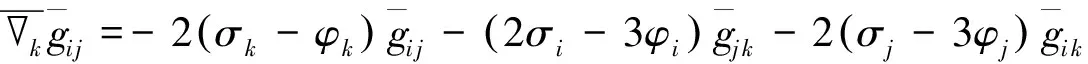
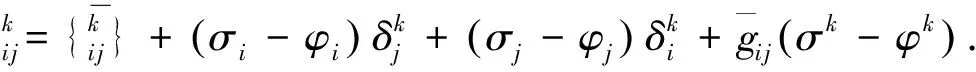

参考文献:
[1] Fridman A, Schouten J A. Uber die Geometric der halb-symmerschen Uber tragungen[J]. Math Zeitschrift, 1924,21:211-233.
[2] Hayden H A. Subspaces of a space with torsion[J]. Proc of London Math Soc, 1932,34:27-50.
[3] Yano K. On semi-symmetric metric connection[J]. Rev Roum Math Purest Appl, 1970,15:1579-1586.
[4] Agache N S, Chafle M R. A semi-symmetric non-metric connection on a Riemannian manifold[J]. Indian J Pure Appl Math, 1992,23(6):309-409.
[5] Zhao P B, Song H Z. An invariant of the projective semi-symmetric connection[J]. Chinese Quarterly J of Math, 2001,16(4):49-54.
[6] Zhao P B. Some properties of projective semi-symmetric connections[J]. International Mathematical Forum, 2008,3(7):341-347.
[7] Ho Talyun. On the projective semi-symmetric connection and conformal semi-symmetric connection on the Riemannian manifold[J]. Journal of Kim II Sung University:Natural Science, 2013,2(2):3-10.
[8] Kurose T. Conformal-projective geometry of statistical manifolds[J]. Interdisciplinary Information Sciences, 2002,8(1):89-100.
[9] Ho Talyun. On a semi-symmetric non-metric connection satisfying Schur’s theorem on a Riemannian manifold[J]. Journal of Kim II Sung University:Natural Science, 2013,2(1):3-7.
[10] Fu F Y, Yang X P, Zhao P B. Geometrical and physical characteristics of a class conformal mapping[J]. Journal of Geometry and Physics, 2012,62(6):1467-1479.
[11] Indranu Suhendro. A new semi-symmetric unified field theory of the classical fields of gravity and electromagnetism[J]. Progress in Physics, 2007,4:47-62.
[12] Han Yanling, Ho Talyun, Zhao Peibiao. Some Invariants of Quarter-symmetric metric connections under projective transformation[J]. Filomat, 2013,27(4):679-691.
