(3,n)型多项式函数方程xf2（x）+xg2（x）=h2（x）的解

黄益生，余锦连

（三明学院信息工程学院，福建 三明 365004）

(3,n)型多项式函数方程xf2（x）+xg2（x）=h2（x）的解

黄益生，余锦连

（三明学院信息工程学院，福建 三明 365004）

讨论在复数域上，当f（x）与g（x）的次数都等于3，并且g（x）的次数不超过3时，多项式函数方程xf2（x）+xg2（x）=h2（x）的解的情况，得到部分结果。主要结果为：如果h（x）的次数等于1，那么这个函数方程无解；如果h（x）的次数等于2，那么这个函数方程一共有8组解；如果h（x）的次数等于3，那么h（x）的1次项系数等于零时，这个函数方程一共有24组解；当h（x）的2次项系数等于零时，但1次项系数不等于零时，这个函数方程一共有36组解。

多项式；多项式函数；函数方程

高等代数教材中一道习题[1]∶对于实系数多项式，等式xf2（x）+xg2（x）=h2（x）成立当且仅当f（x），g（x），h（x）全为零多项式，但是存在不全为零的复系数多项式f（x），g（x），h（x）使得上述等式成立。后一个事实等价于：在复数域上，多项式函数方程xf2（x）+xg2（x）=h2（x）存在不全为零的多项式的解。在文献[2]中，作者对f（x），g（x），h（x）这3个多项式的次数都不超过2的情形，求出了上述函数方程的所有解。本文将探讨当f（x）与g（x）的次数都等于3，并且g（x）的次数不超过3时，上述函数方程的解的情况。将得到g（x）的次数不超过2时的所有解，并得到g（x）的次数等于3时的部分解。主要结果如下：在复数域上，当f（x）与g（x）的次数都等于3时，如果h（x）的次数等于1，那么多项式函数方程xf2（x）+xg2（x）=h2（x）无解；如果h（x）的次数等于2，那么这个函数方程一共有8组解；当h（x）的次数等于3，那么当h（x）的1次项系数等于零的时候，这个函数方程一共有24组解；当h（x）的2次数等于零，但1次项系数不等于零的时，这个函数方程一共有36组解。

1 预备知识

本文中，引用文献[1]中一些熟知的术语和结论，不再另加说明。

命题1[2]设f（x），g（x），h（x）是3个复系数多项式，使得xf2（x）+xg2（x）=h2（x）。

（1）如果h（x）=0，那么g（x）=±i f（x），这里i是虚数单位；

（2）如果h（x）≠0，那么h（x）的常数项等于零；

（3）如果f（x）与g（x）的常数项分别为a0与b0，那么b0=±i a0。

推论1[2]设f（x），g（x），h（x）是3个复系数多项式，如果∂[h（x）]=0,那么xf2（x）+xg2（x）=h2（x）。

命题2[2]设f（x），g（x），h（x）是3个复系数多项式，并设xf2（x）+xg2（x）=h2（x），则

（1)f（x）与g（x）的次数必相等，即∂[f（x）]=∂[g（x）]；

（2）∂[f（x）]≥∂[h（x）]且∂[g（x）]≥∂[h（x）]；

（3）如果∂[f（x）]=m≥0，那么bm=±i am，其中am与bm分别是f（x）与g（x）的首项系数。

注意到虚数单位i的2次幂等于-1，容易验证命题3成立。

命题3设a与b是两个复数，则a+ib=0当且仅当b=i a；a-i b=0当且仅当b=-i a，a2+b2=0当且仅当a+i b=0或a-i b=0。

根据命题2，当f（x）与g（x）的次数不相等时，多项式xf2（x）+xg2（x）=h2（x）无解。为了便于讨论，引用文[2]中术语。

定义1[2]设f（x），g（x），h（x）是数域F上的3个多项式，如果f（x）与g（x）的次数都等于m，并且h（x）的次数等于n，那么称xf2（x）+xg2（x）=h2（x）为一个（m，n）型多项式函数方程。

命题4设f（x），g（x），h（x）是（m，n）型多项式函数方程xf2（x）+xg2（x）=h2（x）的一组解，则f（x），-g（x），h（x）也是它的一组解，反之亦然。

这个命题是显然的，证明从略。

注1：从上一个命题中f（x）的常数项和首项系数分别为a0和am。根据命题1和命题2，当n≥0时，g（x）的常数项b0和首项系数分别bm只能为下列4种情形之一：

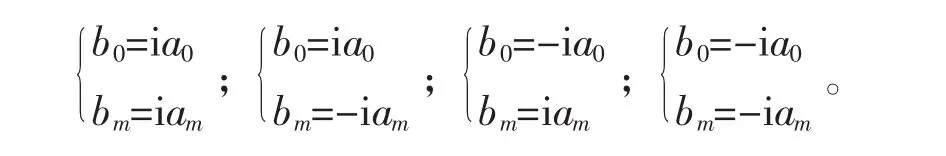
易见，当g（x）的首项系数和常数项为第一种（或第二种）情形时，-g（x）的首项系数和常数项为第四种（或第三种）情形。根据命题4，讨论这样的函数方程的解时，只需讨论前两种情形。当第一种（或第二种）有解时，只需把其解中的g（x）换成-g（x），就得到第四种（或第三种）情形的解；当第一种（或第二种）情形无解时，第四种（或第三种）也无解。

设xf2（x）+xg2（x）=h2（x）是复数域上一个（m，n）型多项式函数方程，其中m≥0。令f（x）的常数项和首项系数分别为a0和am。根据命题1和命题2，这个函数方程有解的一个必要条件为g（x）的常数项和首项系数分别为±i a0和±i am，h（x）的常数项等于零，并且m≥n。

根据本文开头说明，在文献[2]中，作者已经讨论了，在复数域上，当m≤2且n≤2时，（m，n）型多项式函数方程xf2（x）+xg2（x）=h2（x）的解的情况。

本文讨论的时，当这个函数方程的型为（3，n）时，其解的情况。根据命题1，当n=-∞，即h（x）是零多项式时，这样的函数方程有解，其解为g（x）=±i f（x），其中f（x）是任意复系数多项式，根据推论1和命题2，当n=0或n＞3时，这样的函数方程无解。因此只需讨论0＜n≤3的情形。在下面的讨论中，总是假定f（x）=a0+a1x+a2x2+a3x3，其中a3时非零复数。

2 （3,1）型多项式函数方程xf2（x）+xg2（x）=h2（x）的解

假定xf2（x）+xg2（x）=h2（x）是复数域上一个（3,1）型多项式函数方程，其中f（x）=a0+a1x+a2x2+a3x3（a3≠0）。根据命题1和命题2，g（x）的常数项和首项系数分别为±i a0和±i a3，并且h（x）的常数项为零。

当g（x）的常数项和首项系数分别为i a0和i a3时，可设g（x）=i a0+b1x+b2x2+ia3x3且h（x）=c1x（c1≠0），其中b1，b2和c1时待定系数。于是这个函数方程可以写成x（a0+a1x+a2x2+a3x3）2+x（i a0+b1x+b2x2+i a3x3）2=（c1x）2。把等式两边展开，然后合并同类项，得

2a0（a1+i b1）x2+[a12+b12+2a0（a2+i b2）]x3+(2a1a2+2b1b2)x4+[a22+b22+2a3（a1+i b1）]x5+2a3（a2+ib2）x6=c12x2。

因为c1≠0，由（2.1）式，有a1+i b1≠0，从而有a3≠0以及（2.2）式，得a22+b22≠0。另一方面，因为a3≠0，由（2.3）式，有a2+i b2=0，从而由命题3得a22+b22=0，与a22+b22≠0矛盾。这表明，此时所给函数方程无解。

当g（x）的常数项和首项系数分别为i a0和-i a3时，可设g（x）=i a0+b1x+b2x2-i a3x3且h（x）=c1x（c1≠0），其中b1，b2和c1时待定系数。于是这个函数方程可以写成x（a0+a1x+a2x2+a3x）2+x（i a0+b1x+b2x2-i a3x3）2=（c1x）2；即2a0（a1+i b1）x2+[a12+b12+2a0（a2+i b2）]x3+(2a1a2+2b1b2+4a0a3)x4+[a22+b22+2a3（a1-i b1）]x5+2a3（a2-i b2）x6=c12x2。

因为c1≠0，由（2.4）式，有a0≠0，从而有a3≠0，得a0a3≠0。另一方面，由a3≠0以及（2.7）式，有a2-i b2）=0，所以b2=-i a2且a22+b22=0。再由a3≠0以及（2.6）式，得a1-i b1=0，即b1=-i a1，再加上b2=-i a2。因此b1b2=-a1a2。于是由（2.5）式，得a0a3=0，与a0a3≠0矛盾。由此可见，此时所给函数方程无解。

综合上面的讨论，并注意到注1，得到命题5。

命题5在复数域上，（3,1）型多项式函数方程xf2（x）+xg2（x）=h2（x）无解。

3 （3,2）型多项式函数方程xf2（x）+xg2（x）=h2（x）的解

假定xf2（x）+xg2（x）=h2（x）是复数域上一个（3,2）型多项式函数方程，其中f（x）=a0+a1x+a2x2+a3x3（a3≠0）。根据命题1和命题2，g（x）的常数项和首项系数分别为±i a0和±i a3，并且h（x）的常数项为零。

当g（x）的常数项和首项系数分别为i a0和i a3时，可设g（x）=i a0+b1x+b2x2+ia3x3且h（x）=c1x+c2x2（c2≠0），其中b1，b2,c1,c2是待定系数。于是这个函数方程可以写成x（a0+a1x+a2x2+a3x3）2+x（i a0+b1x+b2x2+ia3x3）2=（c1x+c2x2）2。把等式两边展开，然后合并同类项，得

2a0（a1+i b1）x2+[a12+b12+2a0（a2+i b2）]x3+(2a1a2+2b1b2)x4+[a22+b22+2a3（a1+i b1）]x5+2a3（a2+i b2）x6=c12x2+2c1c2x3+c22x4。对照上式等号前后4次项、5次项和6次项的系数，得：

因为c2≠0，由（3.1）式，有a1a2+b1b2≠0，即b1b2≠-a1a2。另一方面，因为a3≠0，由（3.3）式，有a2+ib2=0，所以b2=i a2且a22+b22=0。从而由（3.2）式，得a1+i b1=0，即b1=i a1，再加上b2=i a2，因此b1b2=-a1a2，与b1b2≠-a1a2矛盾。这表明，此时所给函数方程无解。

当g（x）的常数项和首项系数分别为i a0和-i a3时，可设g（x）=i a0+b1x+b2x2-i a3x3且h（x）=c1x+c2x2（c2≠0），于是所给函数方程可以写成x（a0+a1x+a2x2+a3x3）2+x（i a0+b1x+b2x2-i a3x3）2=（c1x+c2x2）2；即2a0（a1+i b1）x2+[a12+b12+2a0（a2+ib2）]x3+(2a1a2+2b1b2+4a0a3)x4+[a22+b22+2a3（a1-i b1）]x5+2a3（a2-i b2）x6=c12x2+2c1c2x3+c22x4。

对照上式等号前后对应次项系数，有

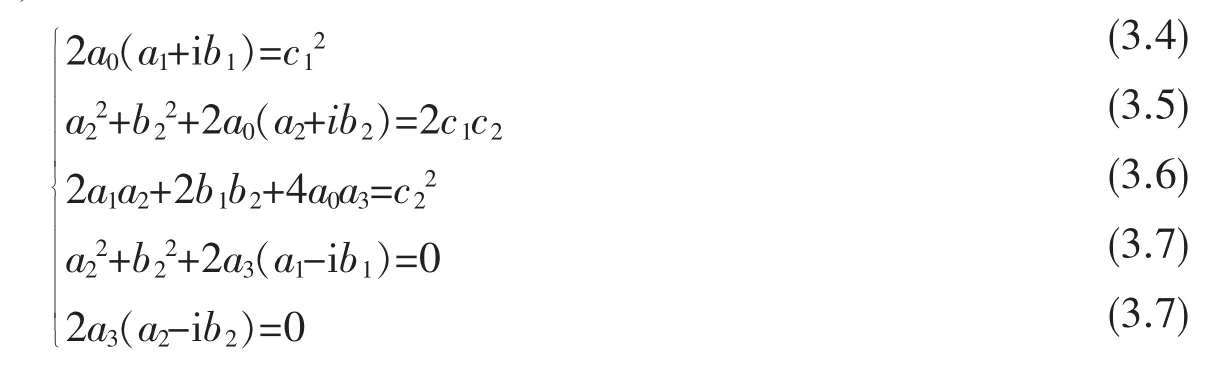
因为a3≠0，由（3.8）式，有a2-i b2=0，从而由命题3，得b2=-i a2且a22+b22≠0。于是（3.7）式变成2a3（a1-i b1）=0，再由a3≠0，得a1-i b1=0，所以b1=-i a2且a12+b12=0。把b1=-i a1与b2=-i a2代入（3.4）和（3.6）两式，可得c12=4a0a1且c22=4a0a3，所以c12c22=16a02a1a3，并且由c2≠0，有a0≠0。另一方面，把b1=-i a1与b2=-i a2代入（3.5）式，得2a0a2=c1c2，所以（c1c2）2=4a02a22。由此可见，当且仅当4a02a22=16a02a1a3时，即a22=4a1a3时，才能保证（c1c2）2=c12c22。换句话说，才能保证所给函数方程有解。现在，当a22=4a1a3时，有a2=±2。已知c12=4a0a1且c22=4a0a3，那么且，所以。由此可见，当c1与c2同号时，有，当c1与c2异号时，有。又已知b2=-i a2，那么当时，有；当时，有

综上所述，当且仅当a22=4a1a3时，所给函数方程有解。当c1与c2同号时，其解一共有2组，它们可以统一用下列公式来表示（其中a0a3≠0）：

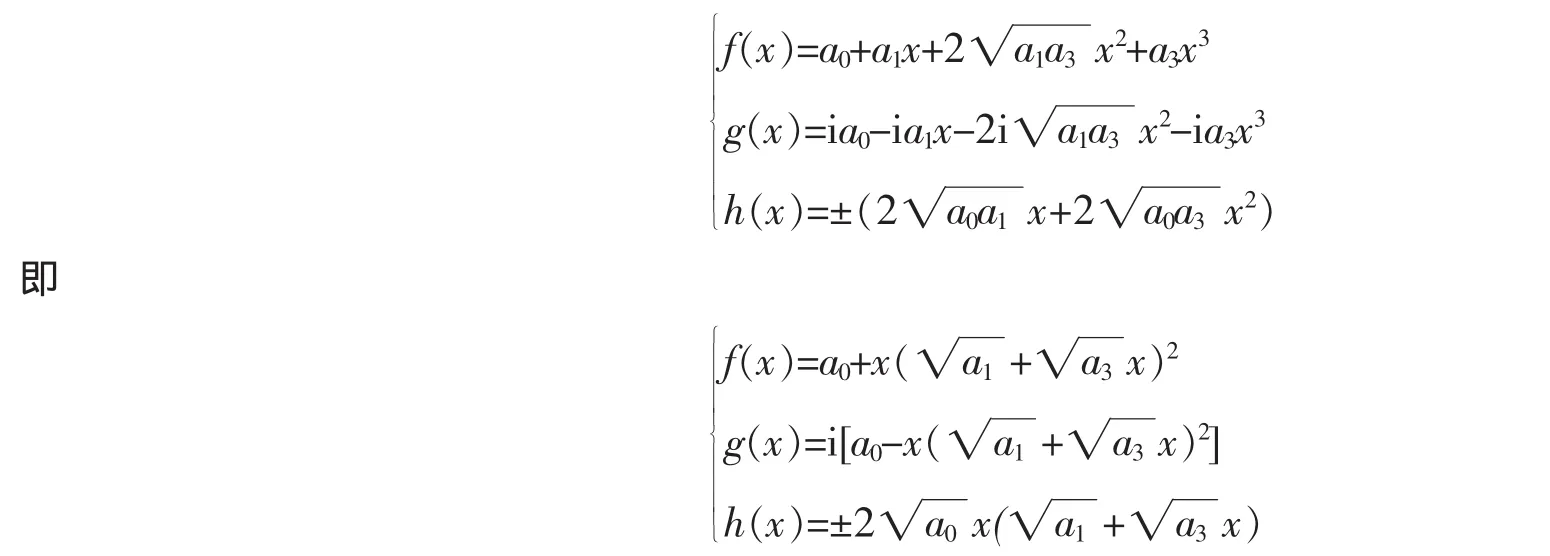
当c1与c2异号时，其解也有2组，它们可以统一用下列公式来表示（其中a0a3≠0）：

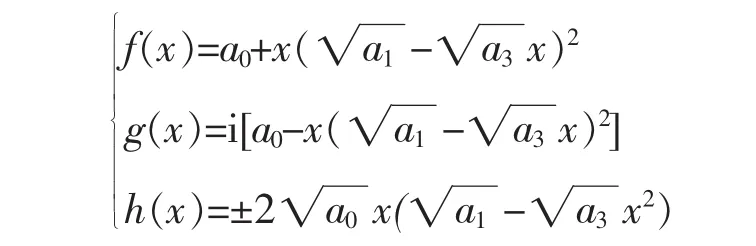
综合上面的讨论，并注意到注1，得到命题6。

命题6在复数域上，（3,2）型多项式函数方程xf2（x）+xg2（x）=h2（x）一共8组解，其解中f（x），g（x）和h（x）的表达式如下（其中a0a3≠0）。

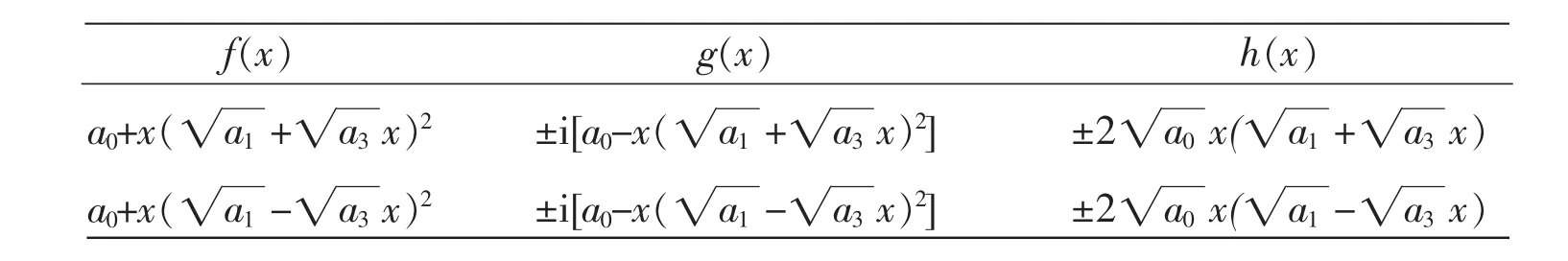
f（x）a0+x（a1■x）2a0+x（a1■+a3■x）2]±i[a0-x（a1g（x）±i[a0-x（a1■+a3h（x）±2 a0■x）±2 a0■x(a1■+a3■-a3■x）2■-a3■x）2]■x(a1■-a3■x）

例1设a0=a1=a3=1，则a0a3≠0。根据命题6，在复数域上，由a0，a1，a3这3个数可以决定（3,2）型多项式函数方程xf2（x）+xg2（x）=h2（x）的8组解，其解得表达式如下：

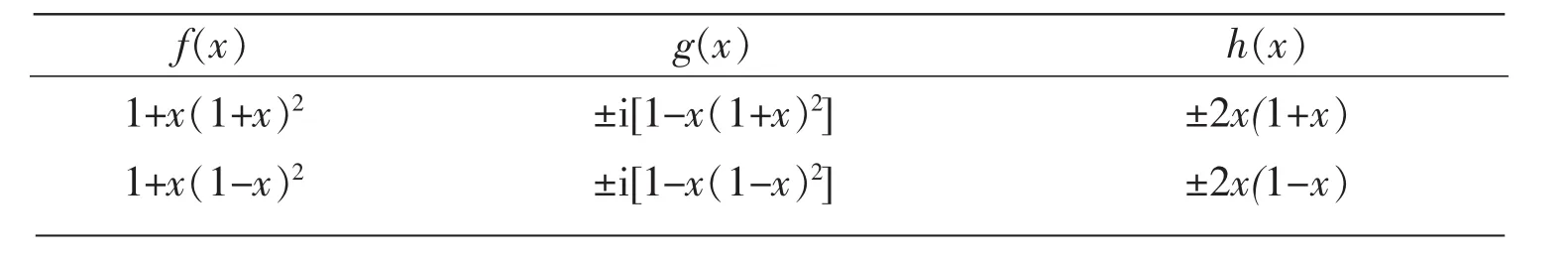
f（x）g（x）h（x）1+x（1+x）2±i[1-x（1+x）2]±2x(1+x）1+x（1-x）2±i[1-x（1-x）2]±2x(1-x）

4 （3,3）型多项式函数方程xf2（x）+xg2（x）=h2（x）的解

假定xf2（x）+xg2（x）=h2（x）是复数域上一个（3,3）型多项式函数方程，其中f（x）=a0+a1x+a2x2+a3x3（a3≠0）。那么g（x）的常数项和首项系数分别为±i a0和±i a3，并且h（x）的常数项为零。由于（3,3）型的情况比较复杂，在下面的讨论中，只得到部分结果，即只得到c1=0或c2=0时的结果。

当g（x）的常数项和首项系数分别为i a0和i a3时，可设g（x）=i a0+b1x+b2x2+i a3x3且h（x）=c1x+c2x2+c3x3（c3≠0），其中b1，b2,c1,c2，c3是待定系数。

（1）如果c1=0，那么这个函数方程可以写成x（a0+a1x+a2x2+a3x3）2+x（ia0+b1x+b2x2+ia3x3）2=（c2x2+c3x3）2；把等式两边展开，然后合并同类项，得2a0（a1+i b1）x2+[a12+b12+2a0（a2+i b2）]x3+(2a1a2+2b1b2)x4+[a22+b22+2a3（a1+i b1）]x5+2a3（a2+i b2）x6=c22x4+2c2c3x5+c32x6。

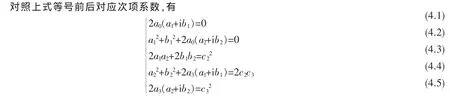
由（4.1）可见，a0=0,或a1+i b1=0。

如果a1+i b1=0，那么a12+b12=0，所以（4.2）式变成a0（a2+i b2）=0。已知c3≠0，那么由（4.5）式，有a2+i b2≠0，因此a0=0。这表明，当c1=0时，总有a0=0。

于是（4.2）式表成a12+b12=0，即（a1+i b1）（a1-i b1）=0，所以（a1+i b1）=0或（a1-i b1）=0。

若a1+i b1=0，则b1=i a1，所以（4.3）式变成2a1（a2+i b2）=c22。用a3去乘最后一式两边，并用a1去乘（4.5）式两边，可得a3c22=a1c32，再加上a3≠0，因此时，由b1=i a1可见，（4.4）式变成。再用（4.5）式左边代替（a2+i b2）。注意到（a2+i b2）≠0，因此。把它代入（4.5）式，得。再由得，其中c2与c3同号。又已知，那么。再加上a0=0，b1=i a1且c1=0，因此当a1+i b1且时，所给函数方程一共有2组解，它们可以统一用下列一组公式来表示（其中a1，a2，a3时满足条件a3≠0且的任意复数）。

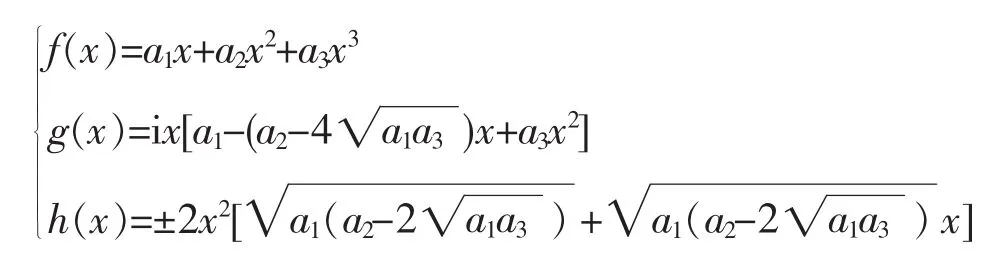
当a1+i b1=0且时，所给函数方程一共有2组解，它们可以统一用下列一组公式来表示（其中a1，a2，a3时满足条件a3≠0且的任意复数）。

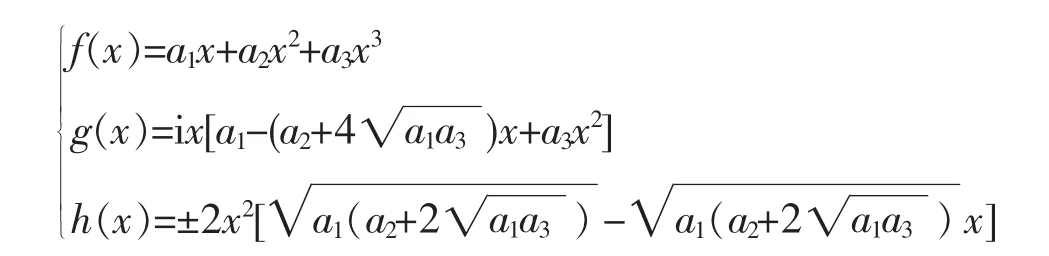
其次，若a1-ib1=0，则b1=-ia1，所以（4.3）式变成2a1（a2-ib2）=c22。把它的两边与（4.5）式两边分别相乘，得4a1a3（a22+b22）=c22c32。另一方面，把b1=-ia1代入（4.4）式，得a22+b22+4a1a3=2c2c3，即（a22+b22）-2c2c3+4a1a3=0。所以4a1a3（a22+b22）-2（4a1a3）c2c3+（4a1a3）2=0。用c22c32代替4a1a3（a22+b22），得c22c32--2（4a1a3）c2c3+（4a1a3）2=0，即（c2c3-4a1a3）2=0，因此，c2c3=4a1a3。用4a1a3代替等式a22+b22+4a1a3=2c2c3右边的c2c3，得a22+b22=4a1a3。这就推出。令Δ=，则b2=±iΔ。当b2=iΔ时，由（4.5）式，有。把它代入等式c2c3=4a1a3，然后用去乘等式的两边，得，显然，a22-Δ2=4a1a3，所以。已知a3≠0，那么当a1≠0时，有注意到，，不难看出，c2与c3必须同号。当a1=0时，由c2c3=4a1a3且c3≠0得c2=0，所以等式仍然成立。再加上a0=0，b1=-ia1且c1=0，因此当a1-ib1=0且b2=iΔ时，所给函数方程一共有2组解，它们可以统一用下列一组公式来表示。

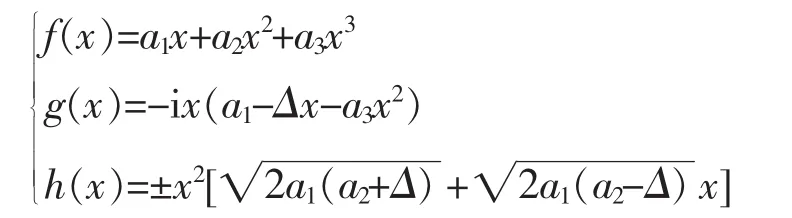
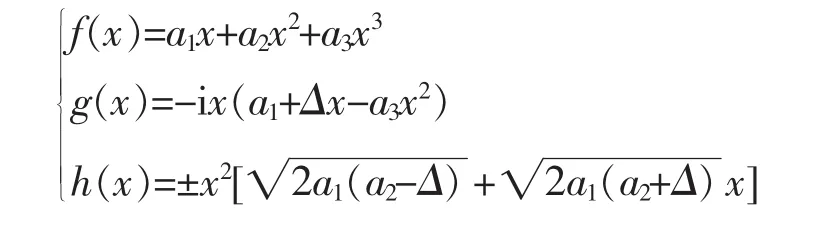
（2）如果c2=0，当c1=0时，这是（1）的特殊情形，因此只需考虑c1≠0的情况。对于这种情况这个函数方程可以写成x（a0+a1x+a2x2+a3x3）2+x（ia0+b1x+b2x2+ia3x3）2=（c1x+c3x3）2；即2a0（a1+ib1）x2+[a12+b12+2a0（a2+ib2）]x3+2（a1a2+b1b2)x4+[a22+b22+2a3（a1+ib1）]x5+2a3（a2+ib2）x6=c12x2+2c1c3x4+c32x6。其中a3c1c3≠0，对照上式等号前后各项系数，有

因为c1≠0且c3≠0，根据（4.6）和（4.10）两式，有a0≠0，a1+ib1≠0且a2+ib2≠0。现在，如果a1-ib1=0，那么a12+b12=0，所以（4.7）式变成2a0（a2+ib2）=0，与a0≠0且a2+ib2≠0矛盾，因此a1-ib1≠0，类似地，由（4.9）式，可得a2-ib2≠0。其次，用a2-ib2去乘（4.6）式两边，得2a0[a1a2+b1b2-i(a1b2-a2b1)]=c12(a2-ib2)。注意到（4.8）式，上式可以改写成2a0[c1c3-i(a1b2-a2b1)]=c12(a2-ib2)，照样地，由（4.8）和（4.10）两式，可以推出2a3[c1c3+i(a1b2-a2b1)]=c32(a1-ib1)。分别用a3和a0去乘最后两个等式，然后把等号两边分别相加，得

再次，用a0c32(a1-ib1)去乘（4.6）式两边，有2a02c32（a12+b12）=a0c12c32(a1-ib1)。用2a02c32去乘（4.7）式两边，然后移项，得2a02c32（a12+b12）=-4a03c32（a2+ib2），所以a0c12c32（a1-ib1）=-4a03c32（a2+ib2）。再用a3去乘最后一式两边，然后对照（4.10）可得a3c12[a0c32(a1-i b1)]=-2a03c34。

类似地，由（4.10），（4.9），（4.6）3式，可以推出a0c32[a3c12(a2-i b2)]=-2a33c14。现在，用a0a3c12c32去乘以（4.11）式两边，然后把最后两个等式代入所得等式，得4a02a32c13c33=-2a34c16-2a04c36，所以a04c36+2a02a32c13c33+a34c16=0，即（a02c33+a32c13）2=0，因此a02c33+a32c13=0，故a02c33=-a32c13。这就推出c33=-a32c13/a02。

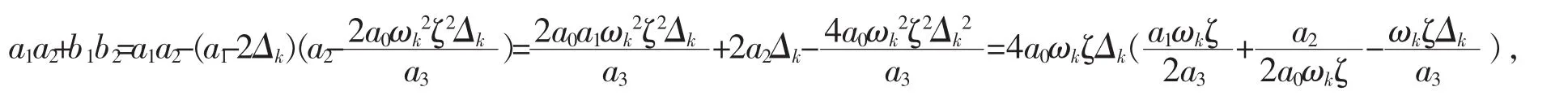
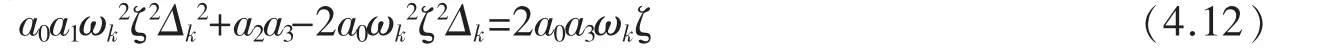
时才能保证（4.8）式成立。换句换说，才能保证所给函数方程有解。已知，那么由

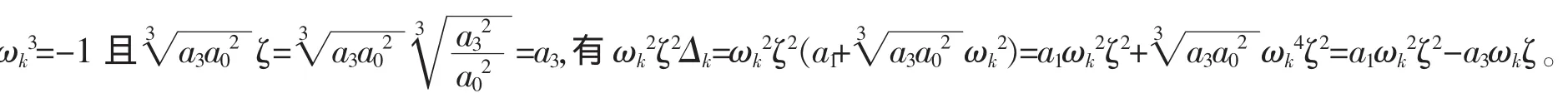
用上式右端代理（4.12）式中的ωk2ζ2Δk，得a0a1ωk2ζ2+a2a3-2a0（a1ωk2ζ2-a3ωkζ）=2a0a3ωkζ，即

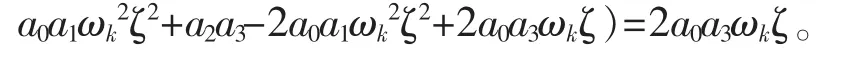
综上所述，如果c2=0，但c1≠0时，那么当且仅当，所给函数方程有解，其解一共有6组，它们可以统一用下列公式来表示：

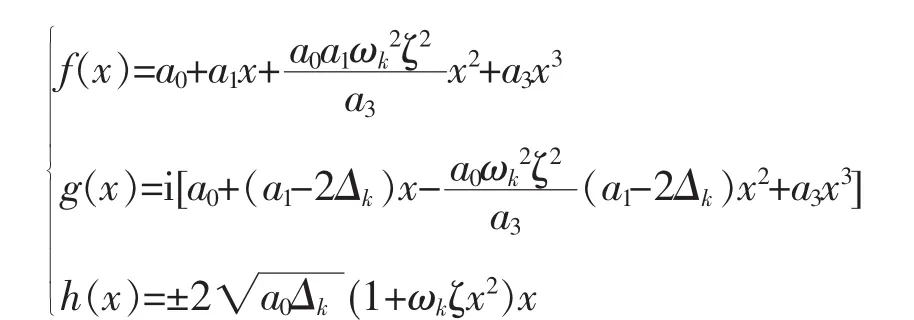
当g（x）的常数项和首项系数分别为i a0和-i a3时，可设g（x）=i a0+b1x+b2x2-i a3x3且h（x）=c1x+c2x2+c3x3c3=ωkc1ζ，所以4a0a1a3c12-a3c14+4a03ωk2c12ζ2。注意到c1≠0，消去上式中的公因式c12，整理得c12=（c3≠0），其中b1，b2,c1,c2,c3是待定系数。

如果a0=0，那么-i a0=i a0。于是所给函数方程就是g（x）的常数项和首项系数分别为-i a0和-i a3时相应的函数方程的特殊情形。根据注1，只需把本节前面的各组解的公式中g（x）的表达式变号，并把这些公式中的a0换成数0，就得到该函数方程的解，因此只需考虑a0≠0的情形。

（1）如果c1=0，那么所给函数方程就是x（a0+a1x+a2x2+a3x3）2+x（i a0+b1x+b2x2-i a3x3）2=（c2x2+c3x3）2；即2a0（a1+i b1）x2+[a12+b12+2a0（a2+i b2）]x3+(2a1a2+2b1b2+4a0a3)x4+[a22+b22+2a3（a1+i b1）]x5+2a3（a2-i b2）x6=c22x4+2c2c3x5+c32x6。所以

因为a0≠0，由（4.13）式，有a1+i b1=0，因此b1=i a1且a12+b12=0.于是由（4.14）式可以推出a2+i b2=0，即b2=ia2。把b1=i a1和b2=i a2代入（4.16）式，得2a1a3=c2c3。两边平方，得4a12a32=（c2c3）2。再把b1=i a1和b2=i a2代入（4.15）和（4.17）两式，得4a0a3=c22且4a2a3=c32。这表明当且仅当4a12a32=4a0a·34a2a3，即a12=4a0a2时，才能保证（c2c3）2=c22c32。换句话说，才能保证所给函数方程有解。当a12=4a0a2时，有。注意到c22=4a0a3且c32=4a2a3，因此且，故。由此可见，当c2与c3同号时，有。此时，，当c2与c3异号时，有。此时，

综上所述，对于c1=0且a0≠0这种情况，当且仅当a12=4a0a2时，所给函数方程有解。当c2与c3同号时，其解一共有2组，它们可以统一用下列公式来表示（其中a2a3≠0）：

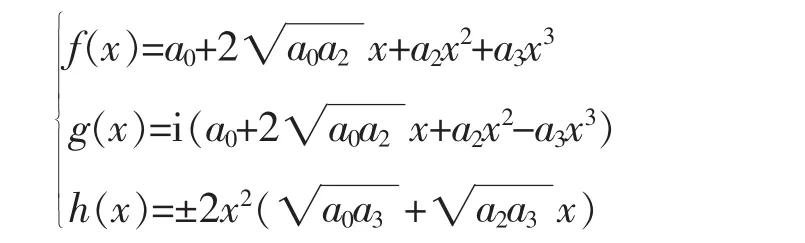
当c2与c3异号时，其解也有2组，它们可以统一用下列公式来表示（其中a2a3≠0）：

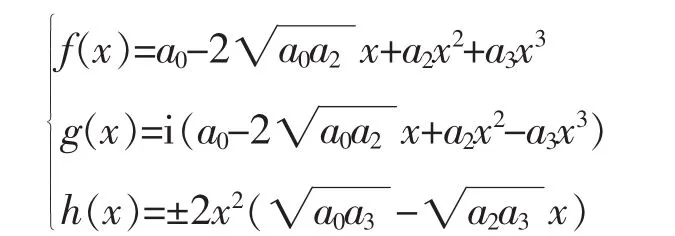
不难看出，当a0=0时，上述两组公式中的多项式仍然是所给函数方程的解。

（2）当c2=0时，根据前面的讨论，只需考虑c1≠0的情况。此时所给函数方程为x（a0+a1x+a2x2+a3x3）2+x（i a0+b1x+b2x2-i a3x3）2=（c1x+c3x3）2；即2a0（a1+i b1）x2+[a12+b12+2a0（a2+i b2）]x3+2(a1a2+b1b2+2a0a3)x4+[a22+b22+2a3（a1-i b1）]x5+2a3（a2-i b2）x6=c12x2+2c1c3x4+c32x6。其中a0a3c1c3≠0。对照前后的对应次项系数，有

因为c1≠0且c3≠0，根据（4.18）和（4.22）两式，有a1+i b1≠0且a2-i b2≠0。

分别考虑a1-i b1=0与a1-i b1≠0这两种情况。

首先考虑a1-i b1=0。对于这种情况，有b1=-i a1且a22+b22=0。从而由a0≠0以及（4.19）式，得a2+i b2=0，即b2=i a2。把b1=-i a1和b2=i a2代入（4.20）式，得2（a0a2+a2a3）=c1c3。两边平方，得4（a1a2+a0a3）2=（c1c3）2。再把b1=-i a1和b2=i a2代入（4.18）和（4.22）式，得4a0a1=c12且4a2a3=c32。因为4（a1a2+a0a3）2-4a0a·14a2a3=4（a1a2-a0a3）2，不难看出，当且仅当上式等于零，即a1a2=a0a3时，才能保证（c1c3）2=c12c32。换句话说，才能保证所给函数方程有解。当a1a2=a0a3时，等式2（a1a2+a0a3）=c1c3可以改写成4a0a3=c1c3，并且由a0a3≠0，有a1a2≠0，从而有，因此等式b1=-i a1变成。另一方面，已知c12=4a0a1且c32=4a2a3，那么。于是

。注意到c1c3=4a0a3，因此c1与c3必须同号。

综上所述，对于这种情况，当且仅当a1a2=a0a3时所给函数方程有解，其解一共有2组，它们可以统一用下列一组公式来表示（其中a0a2a3≠0）：

其次考虑a1-ib1≠0。对于这种情况，由a1+i b1≠0，有a12+b12≠0，从而由（4.19）式，得a2+i b2≠0。用用4a32（a1-i b1）去乘（4.18）式两边，得8a0a32（a12+b12）=2a3c12[2a3（a1-i b1）]。于是由（4.19）和（4.21）两式，有16a02a32（a2+ib2）=2a3c12（a22+b22）。因为a2+i b2≠0，所以16a02a32=c12[2a3（a2-i b2）]。从而由（4.22）式得16a02a32=c12c32，因此c1c3=±4a0a3。另一方面，由（4.18）和（4.22）两式，有

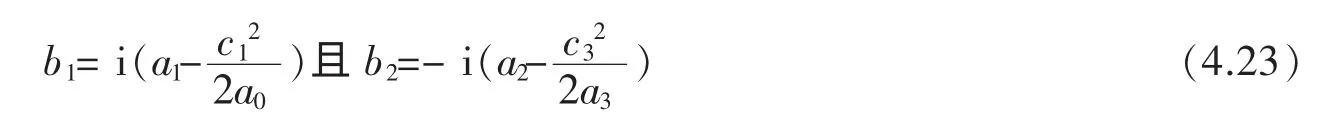
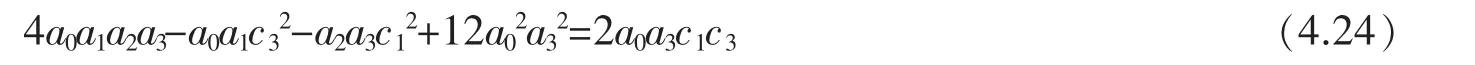
现在，如果c1c3=4a0a3，那么上式可以改写成a0a1a2a3-a0a1c32-a2a3c12+3a0a3c1c3=2a0a3c1c3即

用a2a3去乘等式两边，得（a2a3c1）2-a2a3（a1a2+a0a3）c1c3+a0a1a2a3c32=0，所以（a1a2c3-a0a1a2）（a2a3c1-a0a3c3）=0，因此a2a3c1-a1a2c3=0或a2a3c1-a0a3c3=0故

下面证明a2≠0。事实上，若a2=0，则由（4.25）式，有a0a1c32=a0a3c1c3，从而由c1c3=4a0a3，得4a0a1c32=c12c32。因为c3≠0，所以4a0a1=c12。把最后一式代入（4.23）中的前一式，得b1=-i a1，即a1-i b1=0。这与a1-i b1≠0矛盾。这就证明了a2≠0。再加上a3≠0，因此(4.26)中的两式等价于a3c1=a1c3或a2c1=a0c3。

当a3c1=a1c3时，有a3c12=a1c1c3，从而由c1c3=4a0a3，得a3c12=4a0a1a3，即c12=4a0a1。与上一段的讨论完全一样，可得a1-i b1=0。这与a1-i b1≠0矛盾，所以此时所给函数方程无解。

当a2c1=a0c3时，类似地讨论可以推出，所给函数方程无解。

另一方面，如果c1c3=-4a0a3，那么（4.24）式可以改成4a0a1a2a3-a0a1c32-a2a3c12+12a0a3=-8a02a32，即

a2a3c12-4a0a1a2a3-20a02a32+a0a1c32=0，用c12去乘上式两边，然后用16a02a32代替c12c32，得a2a3c14-4a0a1a2a3c12-20a02a32c12+16a03a1a32=0。因为a3≠0，消去上式各项的公因式a3，得

现在，若a2=0，则由a0a3≠0，上式可化成5c12=4a0a1，即c12=4a0a1/5。因为c1≠0，所以a1≠0。又因为c12c32=16a02a32，（4a0a1/5）c32=16a02a32,从而c32=20a0a32/a1。于是由a2=0容易看出，（4.23）中的两式变成b1=3ia1/5且b2=10i a0a3/a1。把它们代入（4.19）式左边，得这表明，当且仅当4a13-125a02a3=0，即4a13=125a02a3时，才能保证（4.19）式成立。换句话说，才能保证所给函数方程有解。另一方面，当4a13=125a02a3时，有，其中0,1,2。已知b1=3i a1/5且b2=10ia0a3/a1，那么1/ωk=ωk2,得ωk且，即

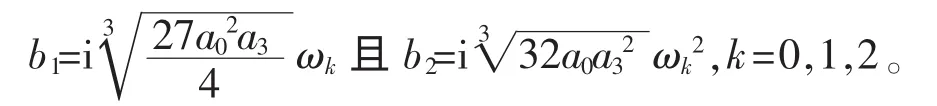
又已知c12=4a0a1/5且c32=20a0a32/a1，那么且，所以且，从而

注意到c1c3=-4a0a3，由上两式容易看出c1与c2异号。

综上所述，对于c1c3=-4a0a3且a2=0这种情况，当且仅当4a13=125a02a3时，所给函数方程有解，其解一共有3组，它们可以统一用下列一组公式来表示：

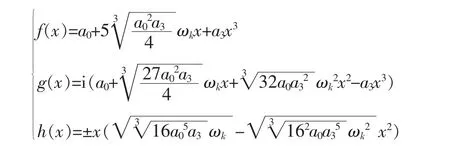
若a2≠0，则由（4.27）式，有，即

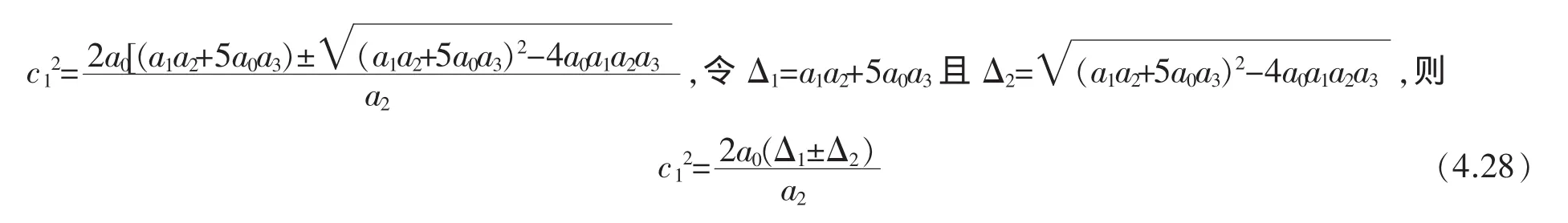
因为c1≠0，由（4.28）式，有Δ1±Δ2≠0。于是当上式中的符号±取正号时，由c12c32=16a02a32，得，显然，那么现在，当（4.28）式中的符号±取正号时，把c12和c32的上述表达式分别代入（4.23）中的两式，得且，即且

因为Δ1=a1a2+5a0a3,所以a1a2-Δ1=-5a0a3，因此。再由c12=。注意到c1c3=-4a0a3。因此c1与c3异号。另一方面，经计算，有

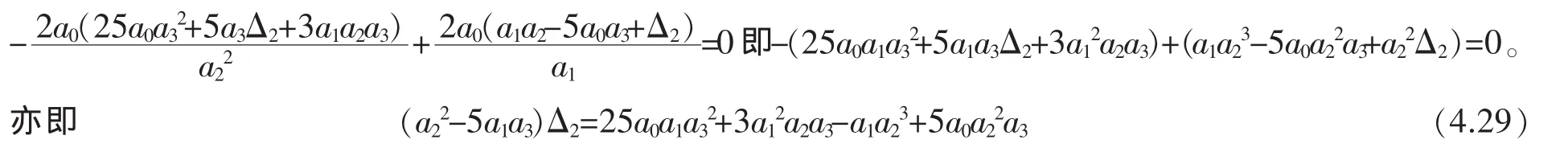
类似地，可以验证，（4.21）式成立当且仅当上式成立。

综上所述，对于c1c3=-4a0a3且a2≠0这种情况，如果（4.28）式中的符号±取正号，那么当且仅当（4.29）式成立时，所给函数方程有解，其解一共有2组，它们可以统一标示成

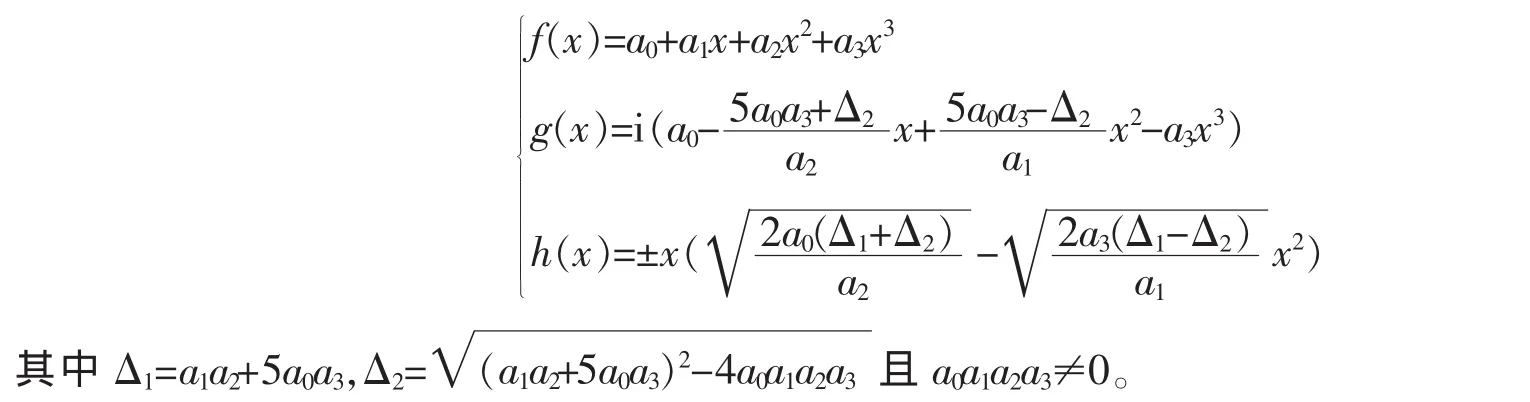
如果（4.28）式中的符号±取负号，类似地可以推出，当且仅当等式（a22-5a1a3）Δ2=-（25a0a1a32+3a12a2a3-a1a23+5a0a22a3）成立时，所给函数方程有解，其解也有2组解，它们可以统一表示成

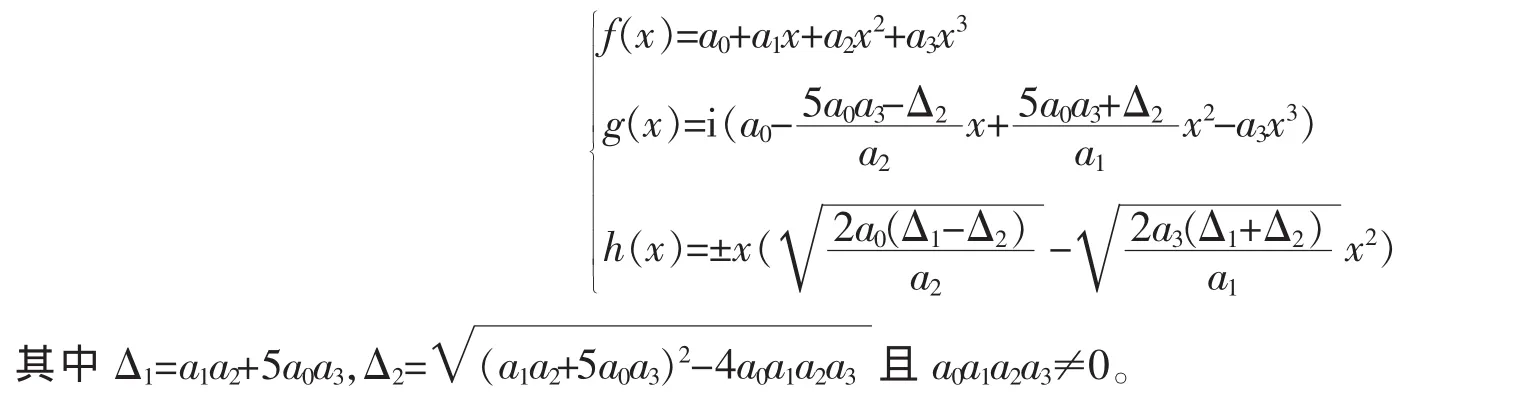
总结上面的讨论，并注意到注1，得到下列2个命题。

命题7设xf2（x）+xg2（x）=h2（x）施复数域上一个（3，3）型多项式函数方程，并设h（x）的1次项系数等于零，则这个函数方程一共有24组解。这些解由两部分组成，前一部分有16组，其解中的f（x）的表达式都是a0+a1x+a2x2+a3x3，并且g（x）和h（x）的表达式如下表示（其中h（x）的最后一项（3次项）系数必须不等于零，符号Δ代表

g（x）±i x[a1-(a2-4 a1a3■)x+a3x2]±i x[a1-(a2+4 a1a3h（x）±2x2[a1（a2-2 a1a3x]±2x2[a1（a2+2 a1a3■■）+a1（a2-2 a1a3■■）■)x+a3x2]±i x（a1-Δx-a3x2）±i x（a1+Δx-a3x2）■x]±x2[2a1（a2+Δ）■）+a1（a2+2 a1a3■■）x]±x2[2a1（a2-Δ）■+2a1（a2-Δ）■■+2a1（a2+Δ）■x]

后一部分有8组，其解得表达式如下表示（表中的a0，a2，a3是任意非零复数）：

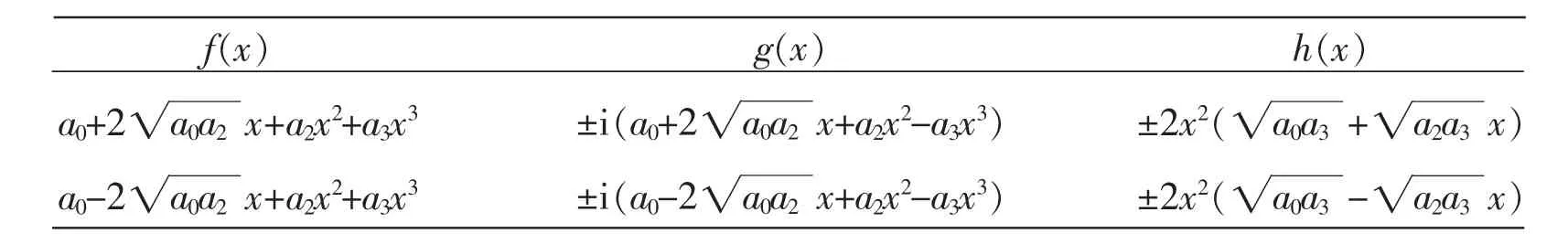
f（x）a0+2 a0a2■x+a2x2+a3x3a0-2 a0a2g（x）±i（a0+2 a0a2h（x）±2x2（a0a3■+a2a3■x+a2x2+a3x3■x+a2x2-a3x3）±i（a0-2 a0a2■x+a2x2-a3x3）■x）±2x2（a0a3■-a2a3■x）

命题8设xf2（x）+xg2（x）=h2（x）是复数域上一个（3，3）型多项式函数方程，并设h（x）的2次项系数等于零，但1次项系数不等于零，则这个函数方程一共有36组解。这些解由4部分组成.第一部分有12组，其解中的f（x）的表达式都是，并且g（x）和h（x）的表达式如下表示。

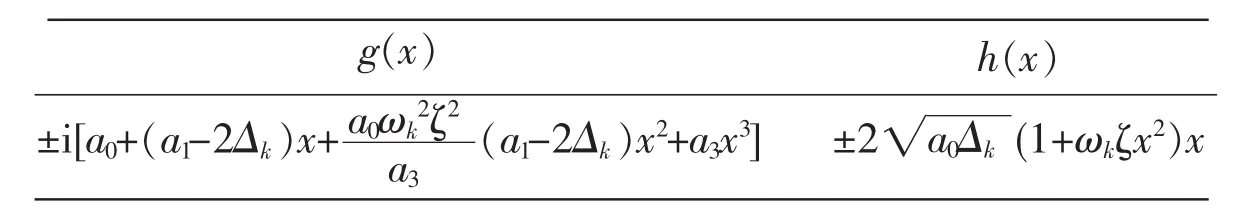
g（x）±i[a0+（a1-2Δk）x+a0ωk2ζ2a3■(1+ωkζx2）x（a1-2Δk）x2+a3x3]h（x）±2 a0Δk

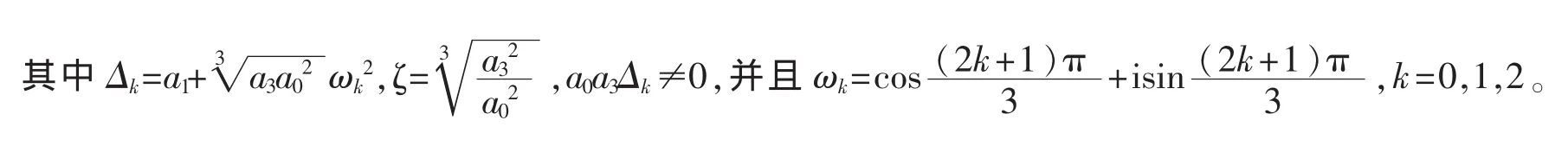
第二部分有4组，其解得表达式如下（表中a0，a2，a3是任意非零复数）。

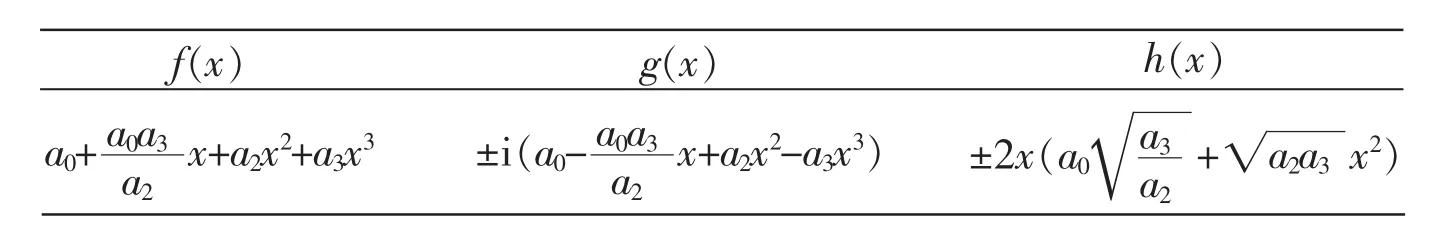
f（x）a0+a0a3 a2 x+a2x2+a3x3g（x）±i（a0-a0a3a2 x+a2x2-a3x3）h（x）±2x（a0a3■+a2a3a2■x2）

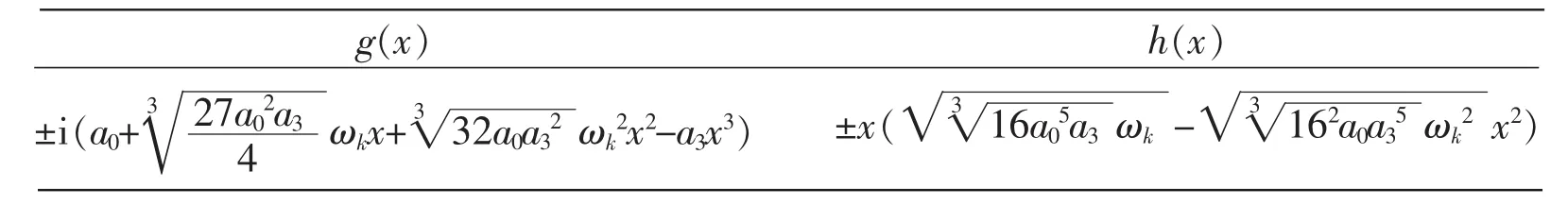
g（x）±i（a0+27a02a33 h（x）±x（16a05a3■ωkx+32a0a323■■ωk2x2-a3x3）■ωk3-162a0a354■■ωk23 x2）

第四部分有8组，其中f（x）的表达式都是a0+a1x+a2x2+a3x3，并且g（x）和h（x）的表达式如下表示。

g（x）±i（a0-5a0a3+Δ2a2 x2-a3x3）±i（a0-5a0a3-Δ2a2 x+5a0a3-Δ2a1 h（x）±x（2a0（Δ1+Δ2）a2■-2a3（Δ1-Δ2）a1■x2）x+5a0a3+Δ2a1 x2-a3x3±x（2a0（Δ1-Δ2）a2■-2a3（Δ1+Δ2）a1■x2）

例1设a1=a2=a3=1。对照命题7中的第一个表，容易看出，在复数域上，由a1，a2，a3这3个数可以决定（3,3）型多项式函数方程xf2（x）+xg2（x）=h2（x）的16组解。这些解中f（x）的表达式都是x+x2+x3，并且g（x）和h（x）的表达式如下表示。

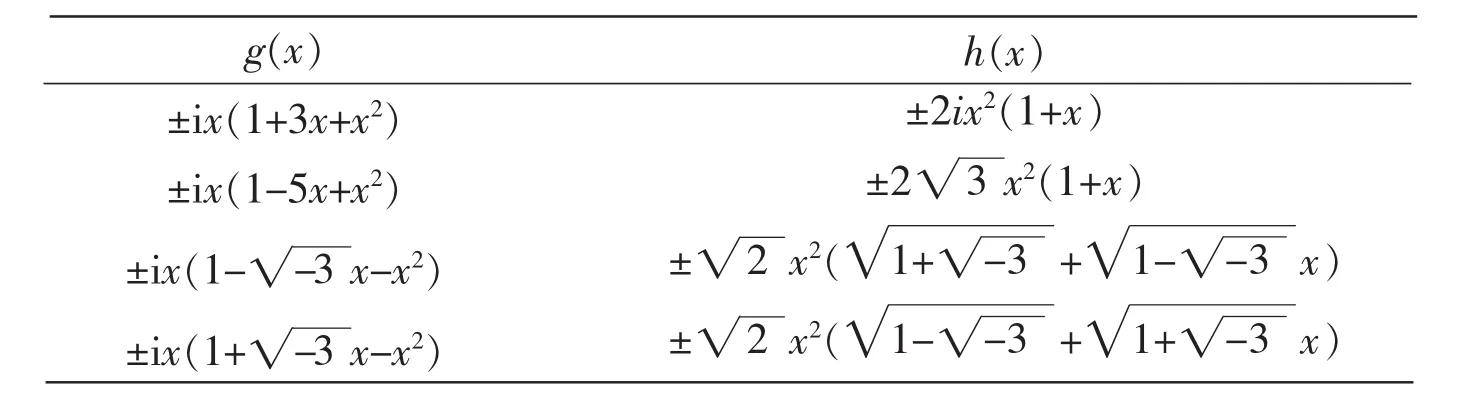
g（x）±i x（1+3x+x2）±i x（1-5x+x2）±i x（1--3 h（x）±2ix2（1+x）±2 3■x2（1+x）±2■x2（1+-3■+1--3■x-x2）±i x（1+-3■■■+1+-3■■x2（1--3■x-x2）■x）±2■x）■

例2设a0=a2=a3=1。对照命题7中的第二个表，容易看出，在复数域上，由这3个数可以决定（3,3）型多项式函数方程xf2（x）+xg2（x）=h2（x）的8组解。其解的表达式如下表示。

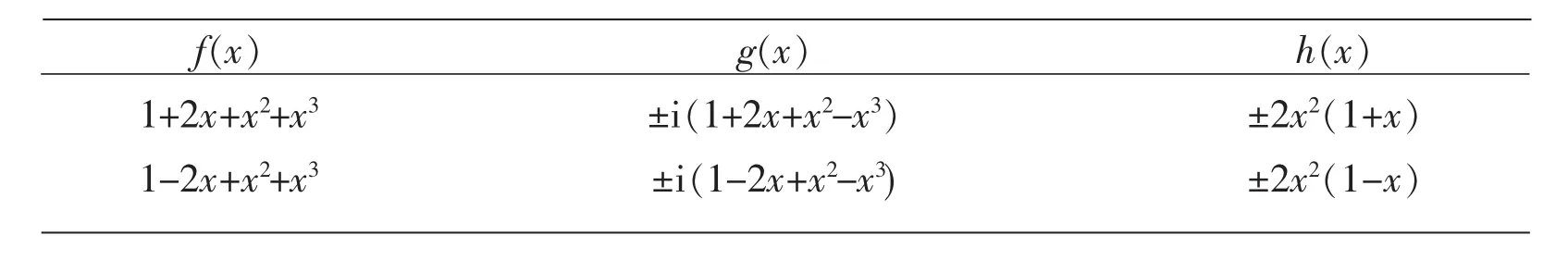
f（x）1+2x+x2+x31-2x+x2+x3g（x）±i（1+2x+x2-x3）±i（1-2x+x2-x3)h（x）±2x2（1+x）±2x2（1-x）

例3设a0=a1=a3=1。对照命题8中的第一个表，容易看出，在复数域上，由a0，a1，a3这3个数可以决定（3,3）型多项式函数方程xf2（x）+xg2（x）=h2（x）的12组解。其解的表达式如下表示（其中ωk=cos

f（x）1+x+ωk2x2+x3g（x）±i[1-（1+2ωk2）x+ωk（2-ωk）x2+x3]h（x）±2 1+ωk2■（1+ωkx2）x

例4设a0=2且a3=1。对照命题8中的第三个表，在复数域上，由a0，和a3这2个数可以决定（3,3）型多项式函数方程xf2（x）+xg2（x）=h2（x）的12组解，其解得表达式如下所示：

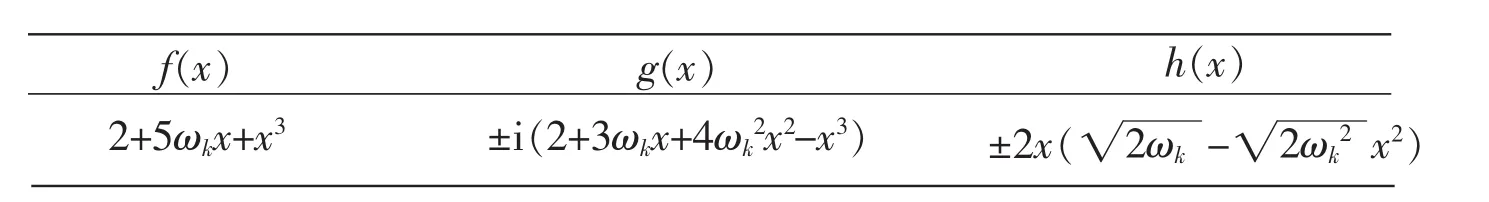
f（x）2+5ωkx+x3g（x）±i（2+3ωkx+4ωk2x2-x3）h（x）±2x（2ωk■-2ωk2■x2）

其中a0与a3是任意复数，且

?

[1]张禾瑞，郝鈵新．高等代数［M］．4版．北京：高等教育出版社，1999．

[2]黄益生，魏文芳．低次多项式函数方程xf2（x）+xg2（x）=h2（x）的解[J]．三明学院学报，2012,29（2）：1-8．

(责任编辑：朱联九)

Solutions of Polynom ial Functional Equation xf2（x）+xg2（x）=h2（x）w ith Type(3,n)

HUANG Yi-sheng,YU Jin-lian
(School of Information Engineering,Sanming College,Sanming 365004,China)

In thispaper,we discuss the situation ofsolutionsof thepolynomial functionalequation xf2（x）+xg2（x）=h2（x）notmore than 3,and obtain partial results.Themain resultsare fellows:if the degreeof h（x）isequal to 1,there is notany solution for the functional equation above;if the degree of h（x）is queal to 2,there are altogether 8 solutions for the same functionalequation;if the degree of h（x）is queal to 3,there are altogether 24 solutions for itwhen the coeffcientof term of the firstdegree of h（x）is queal to zero,and there are altogether 36 solutions for itwhen the coeffcientof term of zhe second degree of h（x）is equal to zero,but the coeffcientof term of the firstdegree of h（x）is not to zero.

polynomial;polynom ia function;functional equation

O 174．14

A

1673-4343（2014）02-0014-13

2013-12-20

福建省教育厅高等学校教学质量工程资助项目（ZL0902／TZ（SJ））

黄益生，男，福建龙岩人，教授。研究方向：代数。