抗拔桩变形及对地铁车站结构计算影响分析

张跃明

(广州地铁设计研究院有限公司，广东广州 5 10010)

0 引言

随着国内地铁建设的大范围开展，建设项目中的抗浮问题也随之越来越突出。目前，地下三层车站及覆土较浅的地下二层车站考虑基于抗浮水位的地下水浮力作用，一般需要设置抗拔桩，用于抗浮及改善结构受力性状等。

目前国内设计院对于地下车站计算模型中抗拔桩的模拟有多种方式。彭帅等［1］将抗拔桩在计算模型中的模拟主要归结为3种:1)将抗拔桩的顶部节点的竖向位移进行约束;2)将剩余浮力作为集中力施加在与抗拔桩相连接的构件上(柱下);3)将抗拔桩视为带自重的梁单元，输入梁单元的刚度带入结构模型进行计算。而胡云华等［2］将抗拔桩作为等效受拉弹簧，弹簧刚度由桩中的钢筋弹性模量和面积确定。

上述文献［1］中第1种模型人为地约束了抗拔桩向上的位移，导致结构各构件所受弯矩的分配与实际情况有较大出入;文献［1］中第2，3种模型及胡云华等的方法只单方面考虑桩体的受力变形，无法考虑桩体与土体的相互作用。因此这些模拟方式均存在局限性，不能反映真实的抗拔桩受力变形性状，这给车站结构的计算也带来一定的偏差，造成结构配筋的不合理。

抗拔桩的有效模拟与其变形性状密切相关，因地铁车站中抗拔桩变形较小，适用于弹性变形，因此研究抗拔桩弹性变形在地铁设计中有着十分重要的理论和实际价值。朱碧堂等［3］总结研究后认为目前国内关于抗拔桩变形的研究也主要集中在弹性变形分析。

黄锋等［4］利用剪切位移原理，假定土为弹性体，桩侧土的变形为一同心圆柱，在抗压桩变形微分方程的基础上，通过微分方程的边界条件得到抗拔桩的变形。很明显，该方法无法考虑桩-土界面的相对滑移，因此有一定的局限性。李熹等［5］根据弹性理论法探讨了抗拔桩的荷载传递机制，通过与实例结果比较，该方法在充分小于极限值时是合适的。

本文研究抗拔桩的弹性变形，提出对抗拔桩采用大刚度弹簧进行模拟，考虑桩-土相互作用，比较符合实际工况。然而对于抗拔桩的研究而言，弹簧刚度如何确定，并未有具体方法。本文将建立抗拔桩的荷载传递模型，推导基于轴向Winkler地基模型的抗拔桩弹性解答，利用弹性力学原理推导抗拔桩桩顶荷载和位移关系的解析式，得出模拟抗拔桩的弹簧刚度计算公式，对影响抗拔桩变形的因素进行分析。

在此基础上，将抗拔桩作为大刚度弹簧的计算模型和其他常用的几种抗拔桩模型进行详细说明，通过实例计算，对这几种模型对地铁车站结构的受力变形计算结果进行对比分析，得出各种模型的受力变形差异，为带抗拔桩的车站结构计算提供指导。

1 抗拔桩弹性变形理论推导

1．1 建立荷载传递模型

荷载传递法也称传递函数法，Seed和Reese［6］首先提出，用来分析桩的荷载传递规律及其沉降计算。这种方法的基本概念是把桩划分为许多弹性单元，每一单元与土体之间用非线性弹簧联系(图1(b))，以模拟桩-土间的荷载传递关系。这些非线性弹簧的应力-应变关系一般称为传递函数。

假定一个长度为L，直径为d的抗拔桩，如图1(a)所示，纵轴为x轴，坐标原点位于桩顶。在桩顶受到荷载Pt作用。此时，桩与土相互作用可采用如图1(b)所示的分析弹簧进行描述［4］。该模型由弹簧和滑块组成，弹簧的刚度为ks，MPa，其物理意义为，在单位长度的桩体表面，由单位剪切位移产生的剪力，滑块提供单位长度土体极限抗力Pu，kN/m。相应的荷载传递模型如图1(c)所示，称为理想弹塑性荷载传递(P-w)模型，其中土体抗力P=πdτ0，τ0为坐标x处桩土界面剪应力，w为x处桩的变形［5］。

当w小于土体屈服变形wu=Pu/ks时，土体处于弹性状态，此时P=ksw;当w≥wu时，土体处于塑性状态，此时 P=Pu=kswu。

图1 抗拔桩的分析模型和荷载传递曲线Fig．1 Analysis model and load transfer curve of uplift pile

ks的影响因素较复杂，主要与桩体和界面的摩擦特性和法向力有关，ks可通过桩荷载试验的P-S曲线反算求得。无试验情况下，也可根据抗拔桩理论分析估算。对于常见桩土条件，Mylonakis［7］研究后认为ks/Gs值为1．4 ～2．5，Gs为土体剪切模量。

1．2 弹性变形解析分析方法

假定桩为弹性材料，桩在外力作用下会产生对应变形，当土为弹性条件时，桩和土的位移相等，桩-土间没有相对位移。从桩身中取一单元体如图2所示。

图2 单元体受力Fig．2 Stressing of cell body

根据单元体的静力平衡条件得到:

式中U为桩截面周长。

桩单元体产生的弹性压缩

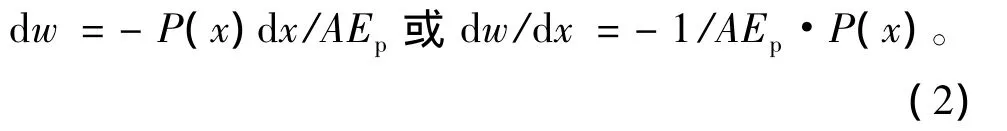
式中A，Ep为桩的截面积及弹性模量。

式中:As为钢筋截面面积，m2;Es为钢筋弹性模量，MPa;Am为桩体中混凝土截面积，m2;Em为桩体中混凝土弹性模量，MPa。

将式(2)求导得:

将式(1)带入式(4)，得:

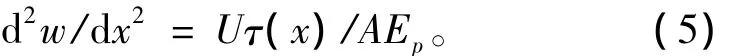
上节的荷载传递模型，Uτ(x)=ksw，d2w/dx2=ksw/AEp，可简化为:

式中 λ2=ks/AEp。

式(6)微分方程的通解为:

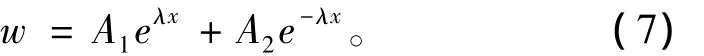
将式(7)带入式(2)，得:

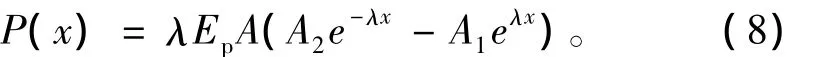
考虑抗拔桩的边界条件:

式中:Pt为桩顶所施加的荷载;L为桩长。

由式(8)，(9)和(10)可得到微分方程的系数为:

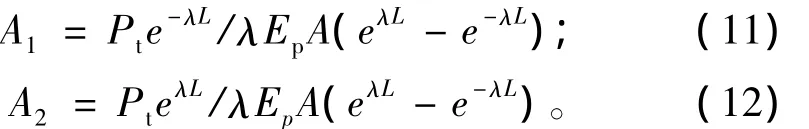
则:

通过运用证伪思维对司法机关所搜集的被害人陈述进行审查,往往能够发现新的破案线索和证据,尤其是有利于发现真正的犯罪实施者。证据的收集与审查判断本身就是互为条件、相辅相成的。被害人陈述有时往往从表面上看是就事论事，但由于它是反映案件事实的直接证据，所以在对其个证与他证关系的审查判断中，通常能从对案件的详细叙述中获得新的破案线索或证据。

桩顶位移

桩的轴力

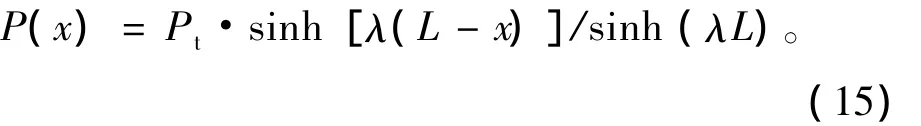
桩的摩擦阻力

由上述式子，可得

式(19)可看作抗拔桩顶弹簧支座的刚度。

由以上分析可以发现，弹簧刚度ks、桩体弹性模量Ep、桩长L、桩径d决定了桩的荷载传递规律。

比值ks/Ep对桩荷载传递规律有重要影响，并通过参数λL具体表现。桩的荷载和位移解中都包含了λL，λL是无量纲量，表示桩-土体系的相对刚度。

2 地铁车站结构计算模型

2．1 抗拔桩顶部节点约束模型

将抗拔桩顶部节点的竖向位移进行约束(仍允许该节点的转动位移)，计算模型见图3。

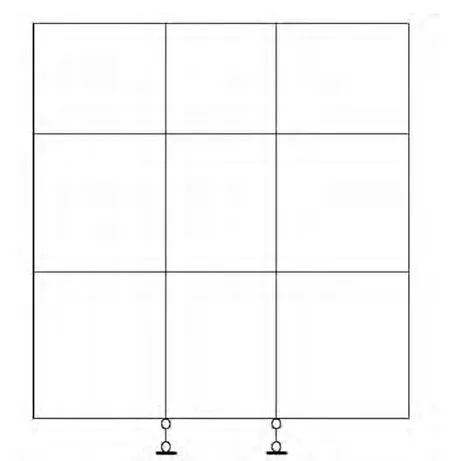
图3 抗拔桩顶部节点约束模型Fig．3 Constraint model of top nodes of uplift pile

从理论上分析，由于抗拔桩的顶端竖向位移被约束，而实际上会有向上的位移，按此模型计算会导致底板中支座的负弯矩及地下负三层侧墙跨中正弯矩被放大，造成配筋浪费。

而实际上，地下车站覆土后，随着地下水位的回升，抗拔桩的抗拔力逐渐增大直至稳定。在较大的抗拔力作用下，无论抗拔桩是否设置有扩大端，其桩身必定会发生变形，桩顶肯定会有向上的位移。这种模型人为地约束了抗拔桩的向上位移，导致结构各构件弯矩的分配与实际情况有较大出入，因此这种计算模型存在较大缺陷。

2．2 梁单元模型

将抗拔桩视为带自重的梁单元，估算其刚度后输入计算模型，计算模型见图4。

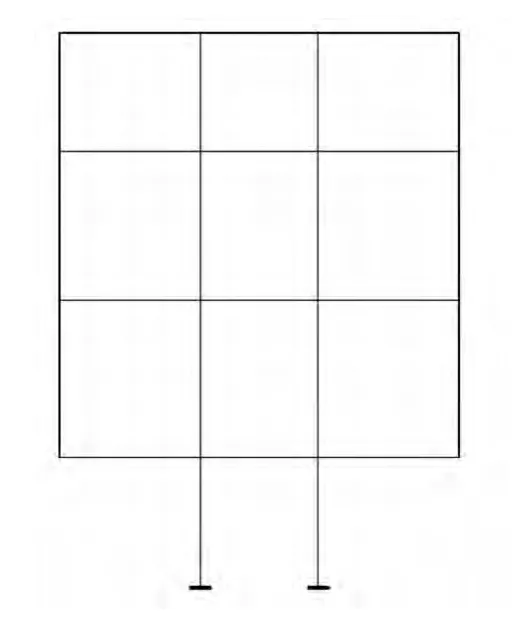
图4 抗拔桩作为梁单元模型Fig．4 Beam element model

该模型只单方面考虑桩体的受力变形，无法考虑桩体与土体的相互作用。桩体刚度也为平均刚度，这是假定沿桩长范围内的轴力均为平均轴力。而实际上桩侧摩阻力的发挥随荷载的增大逐渐向桩深度方向延伸，当上拔荷载较小时，下端桩身范围内未出现桩侧摩阻力，该段桩身轴力为零。该模型有其局限性。

2．3 抗拔桩作为桩-土弹簧模型

该模型假定桩、土均为弹性材料，桩、土位移相等，在第1节中已对此模型做了说明及推导，可将抗拔桩视作桩-土弹簧，弹簧刚度计算见式(19)。计算模型见图5。该模型考虑了桩-土相互作用，比较符合实际工况。

图5 抗拔桩作为桩-土弹簧模型Fig．5 Pile-soil spring model

3 实例计算及分析

以某地下三层车站为例，其剖面见图6，车站结构尺寸见表1，地层参数见表2。

图6 地下3层车站剖面图(单位:mm)Fig．6 Profile of Metro station(mm)

表1 车站结构尺寸表Table 1 Dimension of structure of Metro station

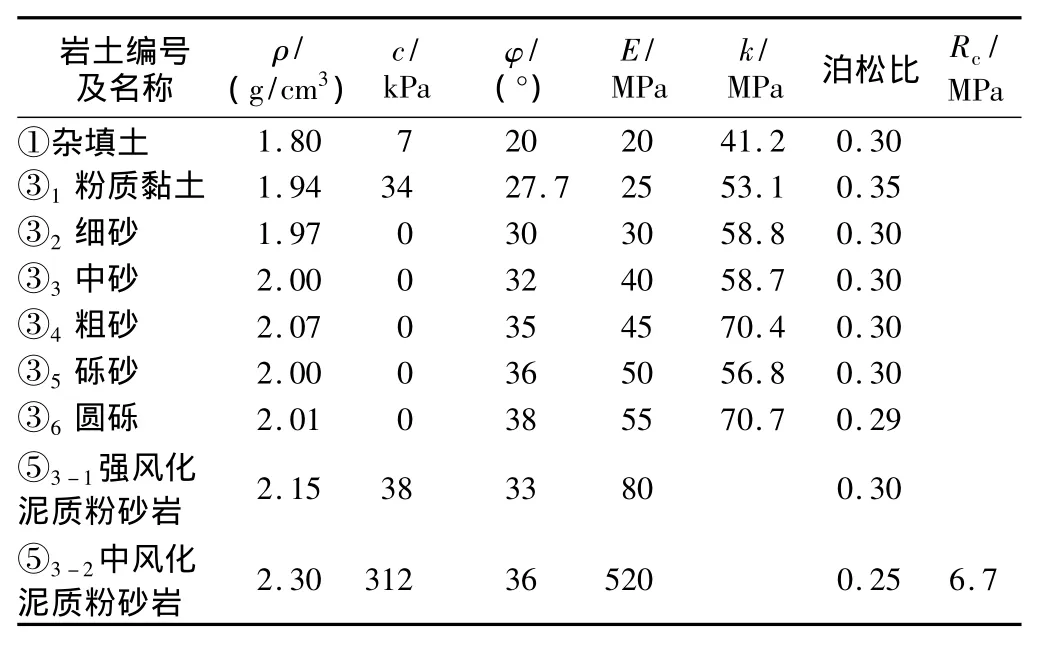
表2 土层物理力学性质表Table 2 Physical and mechanical parameters of strata

3．1 抗拔桩顶部节点约束模型计算

根据《地铁设计规范》［8］，地下结构计算模型为支承在弹性地基上的平面框架结构，基底用土弹簧模拟。约束抗拔桩顶部节点的竖向位移，采用SAP2000软件，取纵向长度1 m为一个计算单元。根据地铁结构一般荷载情况，按水反力工况计算。计算结果见图7。

图7 抗拔桩顶部节点约束模型计算结果Fig．7 Calculation results of model of uplift pile

3．2 抗拔桩作为梁单元模型计算

计算结果见图8。

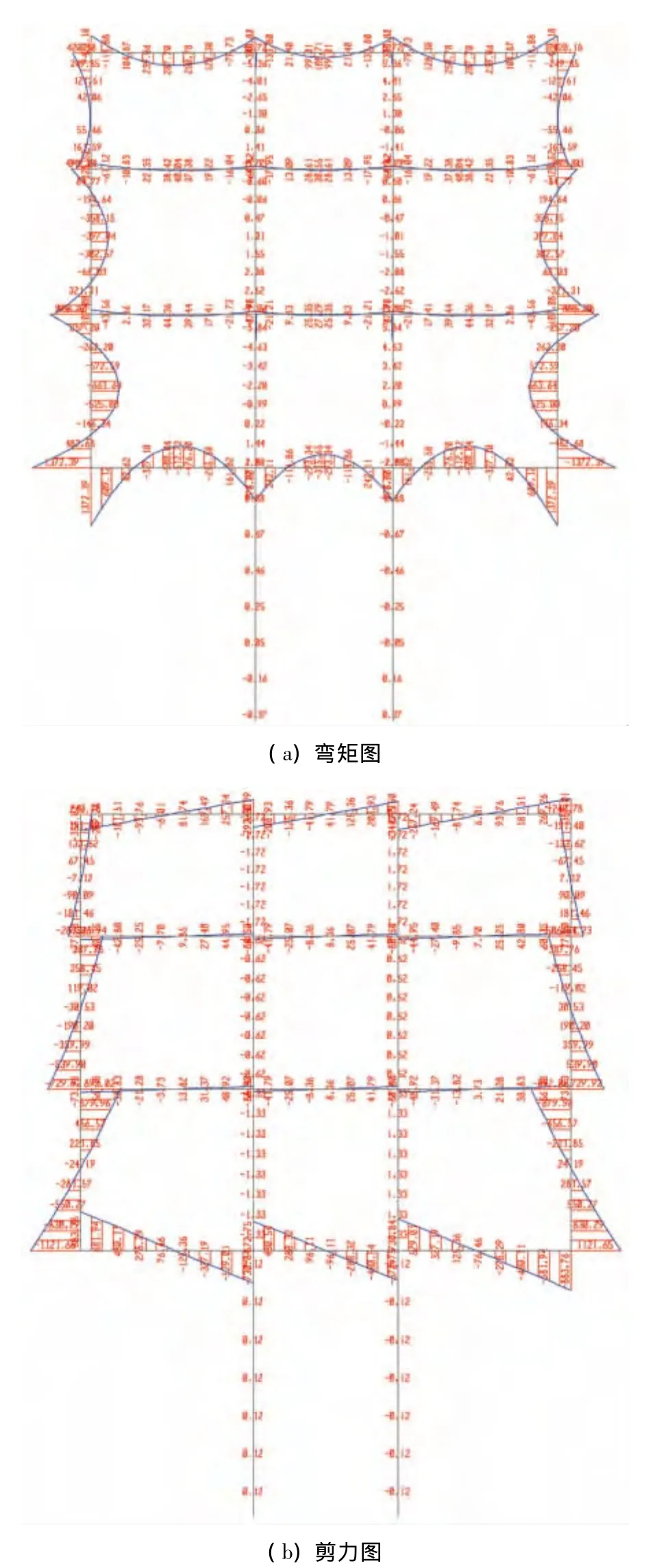
图8 抗拔桩作为梁单元模型计算结果Fig．8 Calculation results of element model

3．3 抗拔桩作为桩-土弹簧模型计算

抗拔桩桩径为1．6 m，桩长为12 m，按《混凝土结构设计规范》［9］，取混凝土强度等级为 C35，弹性模量为31 500 MPa;钢筋采用HRB400，弹性模量为200 000 MPa。配筋率约为2%，钢筋截面积约为0．04 m2，按《建筑桩基技术规范》［10］，桩体弹性模量计算如下。

Gs为土体剪切模量，利用下列公式将变形模量转换为剪切模量Gs，即

取 ks/Gs值约为 2 ．5，则 ks为 8 66．75 MPa。

则 λ =0．11 MN/m。

抗拔桩顶弹簧支座的刚度

将此值带入模型中计算，则计算结果见图9。

图9 抗拔桩作为桩-土弹簧模型计算结果Fig．9 Calculation results of pile-soil spring model

3．4 各模型计算结果对比

各模型计算结果见表3和表4。

最符合实际条件的为弹簧模型。从上述计算结果可以看出:对于跨中弯矩和边支座弯矩，节点约束模型和梁单元模型的计算结果偏于不安全，而对于中支座弯矩，节点约束模型和梁单元模型的计算结果又偏于保守。各模型支座剪力的计算结果相差较小。

表3 车站底板弯矩/剪力计算表Table 3 Calculated bending moment/shearing force of floor slab of Metro station

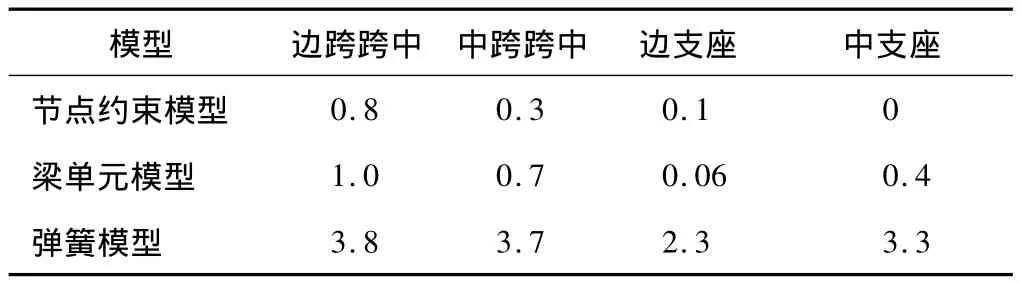
表4 车站底板挠度计算表Table 4 Calculated deflection of floor slab of Metro station mm

从上述计算结果可看出，对于跨中和支座挠度，节点约束模型和梁单元模型的计算结果均偏小。

4 结论与讨论

1)基于弹性理论，推导得出抗拔桩顶弹簧支座的刚度计算公式，弹簧刚度ks、桩体弹性模量Ep、桩长L、桩径d决定了桩荷载传递和变形规律。比值ks/Ep对桩荷载传递规律有重要影响。

2)抗拔桩顶部节点约束模型人为地约束了抗拔桩的向上位移，导致结构各构件所受弯矩的分配与实际情况有较大出入;梁单元模型只单方面考虑桩体的受力变形，无法考虑桩体与土体的相互作用，桩体刚度也为平均刚度;抗拔桩作为桩-土弹簧模型考虑了桩-土相互作用，比较符合实际工况。

3)最符合实际条件的为弹簧模型，对于跨中弯矩和边支座弯矩，节点约束模型和梁单元模型的计算结果偏于不安全，而对于中支座弯矩，节点约束模型和梁单元模型的计算结果又偏于保守。各模型支座剪力的计算结果相差较小。对于跨中和支座挠度，节点约束模型和梁单元模型的计算结果均偏小。

4)把本文推导的模型应用在地铁车站结构计算中，会得出较符合实际条件的受力变形结果。该模型应用有着十分重要的理论和实际价值。

5)桩-土弹簧刚度ks的影响因素较复杂，通过桩荷载试验的P-S曲线反算在实际操作上存在一定难度，若通过理论计算则和实际存在一定的偏差。

6)建议在实际中对抗拔桩和车站结构的受力变形进行大量而广泛的监测，在大量实测数据的基础上不断完善理论计算。

［1］彭帅，王呼佳．抗拔桩在地下车站主体结构计算模型中的边界条件研究［J］．现代城市轨道交通，2012(3):52-58．(PENG Shuai，WANG Hujia．Study on boundary conditions for anti-uplift piles in calculation model for main structure of Metro station［J］．Modern Urban Transit，2012(3):52-58．(in Chinese))

［2］胡云华，郭小红．抗拔桩对隧道主体结构的影响分析［J］．地下空间与工程学报，2011，7(1):93-98．(HU Yunhua，GUO Xiaohong．Analysis for effect of uplift-pile major on major structure of tunnel［J］．Underground Space and Engineering，2011，7(1):93-98．(in Chinese))

［3］朱碧堂，杨敏．抗拔桩变形和极限承载力计算［J］．建筑结构学报，2006，27(3):120-129．(ZHU Bitang，YANG Min．Calculation of displacement and ultimate uplift capacity of tension piles［J］．Journal of Building Structures，2006，27(3):120-129．(in Chinese))

［4］黄锋，李广信，吕禾．砂土中抗拔桩位移变形的分析［J］．土木工程学报，1999，32(1):31-36．(HUANG Feng，LⅠGuangxin，LV He．Analysis of deformation of tension piles in sandy soil［J］．China Civil Engineering Journal，1999，32(1):31-36．(in Chinese))

［5］李熹，凌辉，吴传波．黏土中抗拔桩工作机理分析［J］．工业建筑，2006(S1):707-709．(LⅠXi，LⅠNG Hui，WU Chuanbo．The working mechanism of cohesive soil uplift pile analysis［J］．Ⅰndustrial building，2006(S1):707-709．(in Chinese))

［6］《桩基工程手册》编写委员会．桩基工程手册［M］．北京:中国建筑工业出版社，2008．

［7］Mylonakis．Winkler modulus for axially loaded piles［J］．Geotechnique，2001，51(5):455-461．

［8］GB 50157—2013地铁设计规范［S］．北京:中国建筑工业出版社，2013．

［9］GB 50010—2010混凝土结构设计规范［S］．北京:中国建筑工业出版社，2010．

［10］JGJ 94—2008建筑桩基技术规范［S］．北京:中国建筑工业出版社，2008．