一种基于椭圆曲线的门限部分盲签名方案

汤鹏志，陈仁群，左黎明

（华东交通大学基础科学学院，江西 南昌 330013）

一种基于椭圆曲线的门限部分盲签名方案

汤鹏志，陈仁群，左黎明

（华东交通大学基础科学学院，江西 南昌 330013）

通过对余昭平等人提出的一种基于椭圆曲线上的门限盲签名方案的分析，了解到该方案结合了椭圆曲线、门限盲签名的双重优势。在原方案的基础上提出了一种基于椭圆曲线的门限部分盲签名的方案，不仅保留了原方案的强可验证性性、不可伪造性等安全特性，还进一步增加了签名的稳定性、部分盲性及密钥共享等特性。最后，对新提出的方案进行了可证的安全性分析及效率分析，事实证明该方案安全性高、稳定性好。

椭圆曲线；门限；部分盲性；不可伪造

1982年，David Chuam［1］首次提出了盲签名，把盲签名类比成内嵌复写纸的信封进行传递信息这一事例，并对盲签名的概念及具体实现过程进行了较为详细的论述。盲签名最大的特点就是把消息进行盲化，这可以有效保护签署消息的具体内容，所以它在电子商务和电子选举等领域有着广泛的应用。盲签名一般分为盲化消息、签名盲化消息、对消息进行脱盲三个阶段。根据对消息的盲化程度又把盲签名分为强盲签名和弱盲签名。

1996年Abe等人［2］提出了部分盲签名，为的是解决因盲签名中签名人完全不知道最终签名的任何信息而造成实际应用中数据库无限增长等问题。随后，国内一些研究者也相继提出一些部分盲签名方案。2001年，钟鸣等人［3］率先提出了一种基于比特承诺的部分盲签名方案。2004年，李鸿［4］提出了一种基于椭圆曲线的部分盲签名方案，该方案具有密钥比特数少，在与基于乘法群的密码体制相同条件下安全性更高的特点。2005年，陆洪文等人［5］又提出了一种基于双线性对的门限部分盲签名方案。这里的“门限”是指对于有n个成员的系统中必须至少有t个成员达成协议，共同完成签名。“门限”一词最早是由Desmedt等人［6-7］提出，随后基于Shamir的门限秘密共享思想提出了第一个门限签名方案。该方案进一步扩展了盲签名在电子商务中的应用，它可以让多人同时参与签名。2007年，余昭平等人［8］又在此基础上提出了一种新型的基于椭圆曲线的门限盲签名方案，并且证明了该方案具有盲性、鲁棒性、不可伪造性等安全特性。2008年，闫东升等人［9］提出了一种新的高效的基于身份的部分盲签名方案。2011年，张建中等人［10］又提出了一种随机化部分盲签名方案。2013年，石贤芝等人［11］提出了一种标准模型下高效的门限签名方案。这些方案大多是在前人的基础上做了一些相应的改进。

在电子选票中，很多时候我们只需要从n个选举人中选出t个人进行一场投票选举，这样就防止有些选举人员因个人问题不能来参加选举这一情况，保证选举在规定的时间及场合进行。提出一种新型的基于椭圆曲线的门限部分盲签名方案，它将椭圆曲线、秘密共享及盲签名三者的优势充分结合在一起，适用于电子选举、电子投票及某些军事领域方面。

1 预备知识

1.1 离散对数难题（DLP）与计算Diffie-Hellman难题（CDHP）

假设G是一个加法群，在G上的2个数学难题分别为：

1.2 门限部分盲签名

门限部分盲签名系统是指一个由n个签名者组成的群体，该群体有一个公、私密钥对，群体内任意人数大于等于t个合法、诚实签名者的子群体都可代表这个群体进行签名，并且任意的第三方可利用该群体的公钥进行签名验证。下面是门限部分盲签名方案的主要实现过程：

1）在n个成员的系统中必须至少有t个成员达成协议，共同行使签名权，并且商定共同消息c；

2）每个签名者分别获取自己的公、私钥；

3）用户将被签名的消息m盲化并发送给每个签名者；

4）每个签名者分别用自己的私钥对盲化的消息进行签名，得到签名s，再发送给用户；

5）用户收到签名s后进行脱盲，得到签名s'；

6）任何第三方可以进行验证，并无法获取有关于c的任何消息。

2 基于椭圆的门限部分盲签名方案

2.1 系统参数生成

可信中心CA选取定义在有限域F2p上的一条合适非超奇异的椭圆曲线E，其中，p为一个大素数，使得椭圆曲线群上的离散对数问题是难解的，且P为椭圆曲线E上q阶的基点，公开参数p，q，E，P，接着

为方便描述所提出的椭圆门限签名方案及其安全性分析，我们先给出一个基础的部分盲签名方案，该方案的密钥提取参照了彭庆军［12］等人的方案，在密钥提取阶段嵌入了签名者的身份，提升了方案的稳定性。

2.2 部分盲签名方案

2.2.1 密钥提取

密钥管理中心随机选择t-1阶多项式

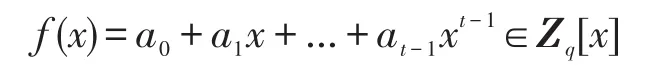
其中：f(0)=a0=d∈Zq为中心私钥；Q=dP为中心公钥。计算

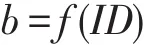
其中：ID是签名者G的身份信息。

把b通过安全信道秘密地发送给相应的签名者G，作为签名者G的私钥，并公开公钥Q'=bP。

对签名者G，验证

若式（1）成立，则签名者G进行对消息签名，否则拒绝签名。

2.2.2 部分盲签名

（签名）签名者G收到h后，计算s=(kH1(c)+h)Q并发送给用户U。

（脱盲）用户U收到s后，计算s'=αs，得到消息m的部分盲签名（r,K,s',m,c)。

2.2.3 签名验证

验证者先计算h=H0(m||c,r)，任何人可以通过下面的等式验证签名的有效性：

若等式（2）成立，则接受该签名，否则拒绝。

2.3 门限部分盲签名方案

在余昭平等人的门限盲签名方案的基础上，提出一种高效安全的门限部分盲签名方案。以下是关于具体方案的执行步骤。

2.3.1 密钥共享协议［12］

密钥管理中心随机选择t-1阶多项式

其中：g(0)=a0=d∈Zq为中心私钥；Q=dP为中心公钥；计算

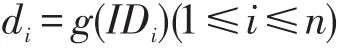
其中：IDi是签名者Gi的身份标识，且每个签名者的身份标识是不同的，即当i≠j时，IDi≠IDj。

把di通过安全信道秘密地发送给相应的签名者Gi，并公开dP,aiP(i=1,2,...,t-1)。

对每个参与者Gi，验证

若式（1）成立，则签名者Gi广播“确认”消息，否则Gi广播“中止”消息。

2.3.2 门限部分盲签名生成协议

根据门限定义，在n个成员的系统中必须至少有t个成员达成协议，才能行使共同签名权，不妨设成员G={G1,G2,...,Gt}t个成员已经达成协议共同行使签名权，并共同协商了公共信息c（签名发布日期、地点及电子货币金额等）。签名过程如下：

1）每个签名者Gi计算：bi=widi，其中，再计算Qi=biP并公开。接着，任取计算Ki=H1(c)kibi(1≤i≤t)并公开。

3）（签名）签名者Gi收到h后，计算si=(kiH1(c)+h)Qi并发送给用户U。

4）（脱盲）用户U收到si后，计算，得到消息m的部分盲签名σ=（r,s,m,c)。

2.3.3 签名验证协议

若等式（2）成立，则接受该签名，否则拒绝。

3 安全性分析

3.1 稳定性

定理1门限部分盲签名方案具有良好的稳定性。

证明该证明可直接参照彭庆军［12］等人的方案。

在新方案中，若后面有新的签名者Gi想加入门限签名协议，可信中心CA只需给新成员提供一个与其他成员人不同的公开身份，并计算签名者的私钥发送给他即可，无需改动系统及之前成员的相关参数。若某个成员想退出该协议，可信中心CA只需广播该成员的ID无效。因此，该方案具有良好的稳定性。

3.2 正确性

定理2门限部分盲签名方案是正确的。

3.3 部分盲性

定理3门限部分盲签名方案是部分盲性的。

证明用户U若要去除签名者Gi的签名中的部分盲因子γ，δ，可这样进行脱盲，计算

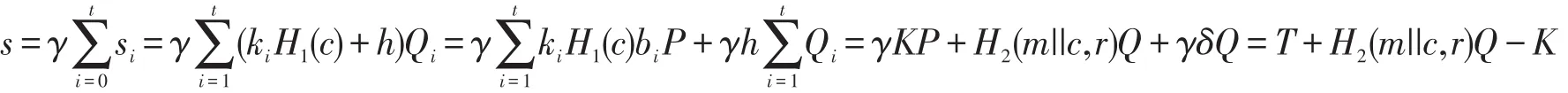
3.4 不可伪造性

这里，我们假设一种最糟糕的情况：即攻击者C可勾结t-1个密钥分享者。接下来，我们参照文献［13］并利用Gennaro［14-15］的思想进行证明。在文献［14］中，Gennaro思想为：如果新的门限盲签名方案是可模拟的，所提出的基础盲签名方案是不可伪造的，则此门限盲签名方案也是不可伪造的。所以，这里我们只需证明：新的门限部分盲签名方案是可模拟的，所提出的基础部分盲签名方案是不可伪造的。即知门限部分盲签名方案是不可伪造的。

下面首先给出定理4，证明所提出的基础部分盲签名方案是不可伪造的：

定理4在随机预言机模型下，假设存在攻击者C能够在t时间内，以ε的优势赢得自适应性下选择密文的游戏，那么，就存在一个算法F，能够在时间内，以O(ε)的优势解决椭圆曲线离散对数问题（ECDLP），其中，τadv表示计算一次逆运算所需要的时间。

证明设算法F收到G中ECDLP实例(P,dP,Q)，其中d∈Zq未知，算法F调用攻击者为子程序去求解d是否成立。

系统设置：F生成系统公共参数(p,q,E,P,Q)，其中系统公钥设置为Q=dP，即用d（未知）模拟系统主密钥。F随机选取ID*∈{0,1}*，再将系统公开参数及ID*一起发送给攻击者C。

询问：需要维护列表L0响应Α的 f询问、L1响应Α的H1询问、L2响应Α的H2询问、LK响应Α的密钥提取询问、LS响应Α的部分盲签名生成询问；q0表示攻击者至多进行 f询问的次数、q1表示攻击者至多进行H1询问的次数、q2表示攻击者至多进行H2询问的次数、qK表示攻击者至多进行密钥提取询问的次数、qS表示攻击者至多进行部分盲签名生成询问的次数。这些列表初始时是空的。具体交互过程如下：

f询问：对 F关于 f(ID)的询问时，若 ID=ID*，则 F随机选取，返回 b*；否则返回 bm(1≤m≤q0)。无论是否有ID=ID*，F都将(ID,b)（其中b=b*或bm）添加到表L0中。

H1询问：对F关于H1(c)的询问时，若在表L1中有(c,h)，则F返回h，否则F随机选取返回，并把(c,h)添加在列表L1中。

H2询问：对F关于H2(m||c,r)的询问时，若在表L2中有(m,c,r,y)，则F返回y，否则F随机选取返回，并把(m,c,r,y)添加在列表L2中。

密钥提取询问：对F关于ID的密钥提取询问（假设已经做过关于ID的 f询问，否则先执行 f询问），F从列表L0中找出项(ID,b)。如果ID=IDm，F宣告失败，算法终止。否则，F计算Q=f(0)P=dP，将(dP,Q)添加到列表L3。

部分盲签名生成询问：当询问(ID,m,c)时，F首先查询列表L0、L1得到(ID,b)和(c,h)，再随机选取s'、，然后计算r=Rx(s'+K-Qy))，并定义H2(m||c,r)=y，最后若在列表L2中有(m,c,r,y)，则F终止并输出失败，否则F将(r,K,s')发送给C，并将(m,c,r,y)添加到列表L2中。

伪造：最后，如果算法F没有终止，则C在没有做过密钥提取询问和部分签名询问的条件下，以一个不可忽略的概率ε对一个输入消息m输出对应的有效部分盲签名（r,K,s',m,c)。根据Forking引理［16］，通过对C哈希重放，存在有效的算法S可以获得两个关于消息m及c的有效签名（r1,K1,s1',m,c)和（r2,K2,s2',m,c)，其中r1≠r2。结合这两个有效的部分盲签名，算法S能以一个不可忽略的概率解决ECDLP，从而反证所提出的门限部分盲签名方案是不可伪造的。证明步骤如下：

给定椭圆曲线上的一个任意二元组（P,Q)，令Q=aP。待算法S与攻击者C执行了多项式次部分盲签名协议后，算法S得到两个有效的部分盲签名（r1,K1,s1',m,c)和（r2,K2,s2',m,c)，其中r1≠r2。即有下面2个等式

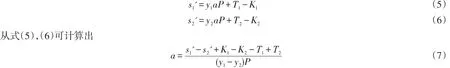
从而算法S解决了ECDLP。

在的计算时间方面，每次签名询问都是最多需要1次双线性对逆运算。所以

其中：τ表示回答一个H提问所需要的时间。

然后，我们先给出一个等价定义：

定义［14］所提出的门限部分盲签名方案是可模拟的，等价于以下两个条件成立：

1）密钥共享协议算法是可模拟的。存在模拟器1，当输入中心公钥Q和被攻击者勾结的t-1个成员的私钥d1,d2,...,dt-1时，能够模拟攻击者在密钥共享协议算法中输出Q的全过程。

2）门限部分盲签名生成算法是可模拟的。存在模拟器2，当输入公钥Q、消息m、公共消息c和它的签名（r,s,m,c)，t-1个成员的私钥d1,d2,...,dt-1时，能够模拟攻击者在门限部分盲签名生成算法中输出σ=（r,s,m,c)的全过程。

最后，给出定理5并证明第三部分所提出的方案是抗攻击的。

定理5［13］在计算Diffie-Hellman难题假设下，即使攻击者勾结t-1个成员，这里提出的新方案仍是安全的。

证明根据Gennaro的思想，下面我们只需证明门限部分盲签名方案是可模拟的。

不失一般性，假设攻击者C成功勾结了t-1个成员G1,G2,...,Gt-1。

1）证明门限密钥生成算法是可模拟的。模拟器1［13］拥有中心公钥Q和被勾结的t-1个成员的私钥d1,d2,...,dt-1及d，再根据等式

模拟器1可以反算出Qt=btP，并类似地计算出Qi=biP(i=t+1,...,n)。所以模拟器1可以模拟攻击者在密钥共享协议算法中输出Q的全过程。

2）证明门限签名算法是可模拟的。设模拟器2拥有盲消息m、部分盲签名σ=（r,s,m,c)、被勾结的t-1个成员的私钥d1,d2,...,dt-1及d。模拟器2可以从d1,d2,...,dt-1计算出消息m的子签名si=(kiH1(c)+h)Qi(i=1,2,...,t-1)，根据等式

模拟器2可以反算出σt=（rt,st,m,c)，类似地计算出σi=（ri,si,m,c)(i=t+1,...,n)。所以模拟器2可以模拟攻击者在门限部分盲签名生成算法中输出σ=（r,s,m,c)的全过程。

综上，可知该方案是不可伪造的。

4 效率分析

表1是将文献［8］所提的方案与本方案的效率分析，通过通信量与计算量两方面的指标进行了明确的对比。为方便叙述，给出以下标记：tH、tM、tE(∙)、tE(+)、tI分别代表计算哈希函数的运算时间、模乘的运算时间、椭圆曲线上加法运算时间、椭圆曲线上点乘运算时间及求逆运算时间。至于一般的加减法运算，和一般的数乘运算所需时间表中忽略不计。

表1 文献［8］及本方案的效率分析对比Tab.1 Efficiency contrast between reference［8］and the proposed scheme

5 结束语

随着电子信息时代的迅速发展，电子商务、电子选举、电子支付、电子政务等越来越普遍，信息安全就显得尤为重要。本文提出的方案是结合了椭圆曲线、门限方案及部分盲签名提出的一种基于椭圆曲线上的门限部分盲签名，这个方案具有短密钥、签名人数自由及部分盲性等特点，并进一步扩展了盲签名的应用范围，在一定程度上解决了盲签名在匿名性与可控性之间的矛盾。最后，借鉴Gennaro的思想对其进行了详细的安全性分析，证明了该方案是安全可行的。

[1]CHAUM D.Blind Signature for Untraceable Payments[C]//Proceeding of Advance in Crytology-EUROCtypto’82,Plenum Press, 1983:199-203.

[2]ABEm,FUJISAKI E.How to Date Blind Signature[C]//Proceedings of Advances in Cryptology-Asiacrypt’96,LNCS,Springer, 1996:244-251.

[3]钟鸣,杨义先.一种基于比特承诺的部分盲签名方案[J].通信学报,2001,22(9):1-6.

[4]李鸿.一种基于椭圆曲线的部分盲签名方案[J].宿州师专学报,2004,19(1):89-91.

[5]陆洪文,郑卓.基于双线性对的门限部分盲签名方案[J].计算机应用,2005,25(9):2057-2059.

[6]DESMEDT Y,FRANKEL Y.Threshold cryptosystems[C]//Advances in Cryptology-Crypto 89,Lectures Notes in Computer Sci⁃ence 435,Berlin:Springer-Verlag,1989:307-315.

[7]DESMEDT Y.Threshold cryptosystems[J].European Trans on Telecommunications,1994,5(4):449-457.

[8]余昭平,康斌.基于椭圆曲线的新型可验证门限盲签名方案[J].计算机工程,2007,33(23):161-162.

[9]闫东升.一个新的高效的基于身份的部分盲签名方案[J].计算机工程与应用,2008,44(2):137-139.

[10]张建中,马冬兰.一种高效的门限部分盲签名方案[J].计算机工程,2012,38(1):130-134.

[11]石贤芝,林昌露,张胜元,等.标准模型下高效的门限签名方案[J].计算机应用,2013,33(1):15-18.

[12]彭庆军.一种基于椭圆曲线的可验证门限签名方案[J].通信技术,2008,3(41):104-106.

[13]周萍,何大可.一种CDH难题的强壮门限盲签名方案设计[J].计算机应用研究,2011,28(2):704-707.

[14]GENNARO R,JARECKI S,KRAWCZYK H,et al.Robust threshold DSS signatures[C]//Lectures Notes in Computer Science,Ber⁃lin:Springer-Verlag,1996:354-371.

[15]GENNARO R,JARECKI S,KRAWCZYK H,et al.Secure distributed key generation for discrete-log based cryptosystems[C]// Lectures Notes in Computer Science,Berlin:Springer-Verlag,1999:295-310.

[16]POINTCHEVAL D,STERN J.Security arguments for digital signatures and blind signatures[J].Journal of Cryptology,2000,13(3): 316-396.

A Threshold Partially Blind Signature Based on ECDLP

Tang Pengzhi,Chen Renqun,Zuo Liming
(School of Basic Science,East China Jiaotong University,Nanchang 330013,China)

The threshold blind signature based on ECDLP presented by Yu et al.combines advantages of elliptic curve signature and blind threshold signature.This study proposes a new threshold partially blind signature based on ECDLP,which not only keeps strong-verification and unforgeability,but also further increases stability and key sharing.Through provable security and efficiency analysis,it verifies the higher safety and good stability for the proposed new scheme.

elliptic curve;threshold;partially blind signature;unforgeability

TP301

A

2014-09-22

国家自然科学基金项目（11361024，11061014）；江西省教育厅科技项目（GJJ13339）；华东交通大学校立科研基金项目（11JC04）

汤鹏志（1961—），男，教授，主要研究方向为信息安全。

1005-0523（2014）06-0096-07