基于三次B样条有限元法的BBMB方程数值解
2014-08-01徐莹莹周丽萍樊强朴光日
徐莹莹,周丽萍,樊强,朴光日
(延边大学理学院 数学系,吉林 延吉 133002)
Benjamin-Bona-Mahony-Burgers(BBMB)方程
(1)
表示的是小振幅长波在非线性色散介质中的传播[1],其中α>0,β是任意常数,f是一个外力.在物理学中,系统(1)的色散效应与方程Benjamin-Bona-Mahony(BBM)相似,其损耗效应与Burgers方程相似,并且BBMB方程是Korteweg-de Vries-Burgers(KdVB)方程的另一种形式[2].文献[3-6]、[7-9]和[10-11]分别采用有限元、有限差分和Adomain分解方法研究了该方程的数值解;文献[12-13]应用二次B样条有限元法求解了Burgers方程的数值解;文献[14]采用三次B样条配置法求解了BBMB方程的数值解.本文应用三次B样条有限元法先把BBMB方程转化为非线性常微分方程,然后利用Crank-Nicolson差分法进行时间离散化,从而得到了全离散化的代数方程.
1 数值格式
在整个空间域中,标准的拉格朗日有限元基函数只能提供简单的C0-连续,因而不适合应用于高阶微分方程的离散化,比如三阶或四阶微分方程; 但由于B-样条基函数至少满足C1-连续,因此可用于求解高阶微分方程的近似解.
根据变分方法可将系统(1)转化为弱形式:
(2)

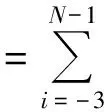
(3)
其中αi(t)是待定系数,Bi(x)是三次B样条有限元基函数.在区间[0,L]上定义Bi(x)为
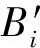

表1 基函数及其一阶、二阶导数在各结点的值

(4)

(5)
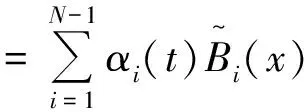
(6)

(7)
将(7)式转化为矩阵形式后得
(8)
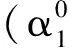

(9)

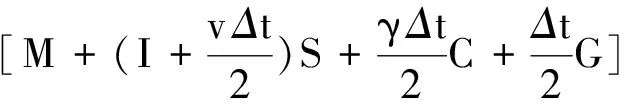
(10)
M,S,C是常数矩阵,由于矩阵G依赖于时间,因此其每一步骤都需要重新计算.向量αn的时间演化确定近似解uh(x,t)的时间演化,当已知初始向量α0的情况下,此演化过程是通过反复计算系统(10)来完成的,其具体过程如下:
1)时间t=0时,首先,根据已知初始向量α0得到近似的G,并由(10)式计算近似的α1.然后,通过α=(1/2)(α0+α1)重新计算G,接着由(10)式再计算α1.反复进行20次左右的这种迭代可以得到比较精确的α1.
2)时间t>0时,首先,通过α=αn+(1/2)(αn-αn-1)求得G,并由(10)式计算得到αn+1的近似值.然后,利用α=(1/2)(αn+αn+1)重新计算G,接着由(10)式再计算αn+1.通过反复迭代10次可以得到精确的αn+1.
2 稳定性分析
根据典型的傅里叶模式的增长因子的Von-Neumann理论,定义

(11)
其中k是模型数,h是区间步长.数值格式(10)的稳定性取决于其线性化.在非线性项u ux中,假设u是局部常数,则其等价于假设对应的值αj也是常数并等于d; 因此,格式(10)相应的线性递推关系式可由下式给出:

(12)


(13)

3 数值验证
为了验证本文算法的有效性和精确性,考虑如下两种情况.
例1 给定参数α=1,β=1,初始条件为u0(x)=4x(1-x)sinπx,Δt=0.05,在不同时间段、结点和区间步长的条件下,观察BBMB方程的数值解.
解例1结果见表2.

表2 不同时刻、区间步长条件下各结点的近似值

解图1和图2分别表示近似解在不同参数下的演化过程.
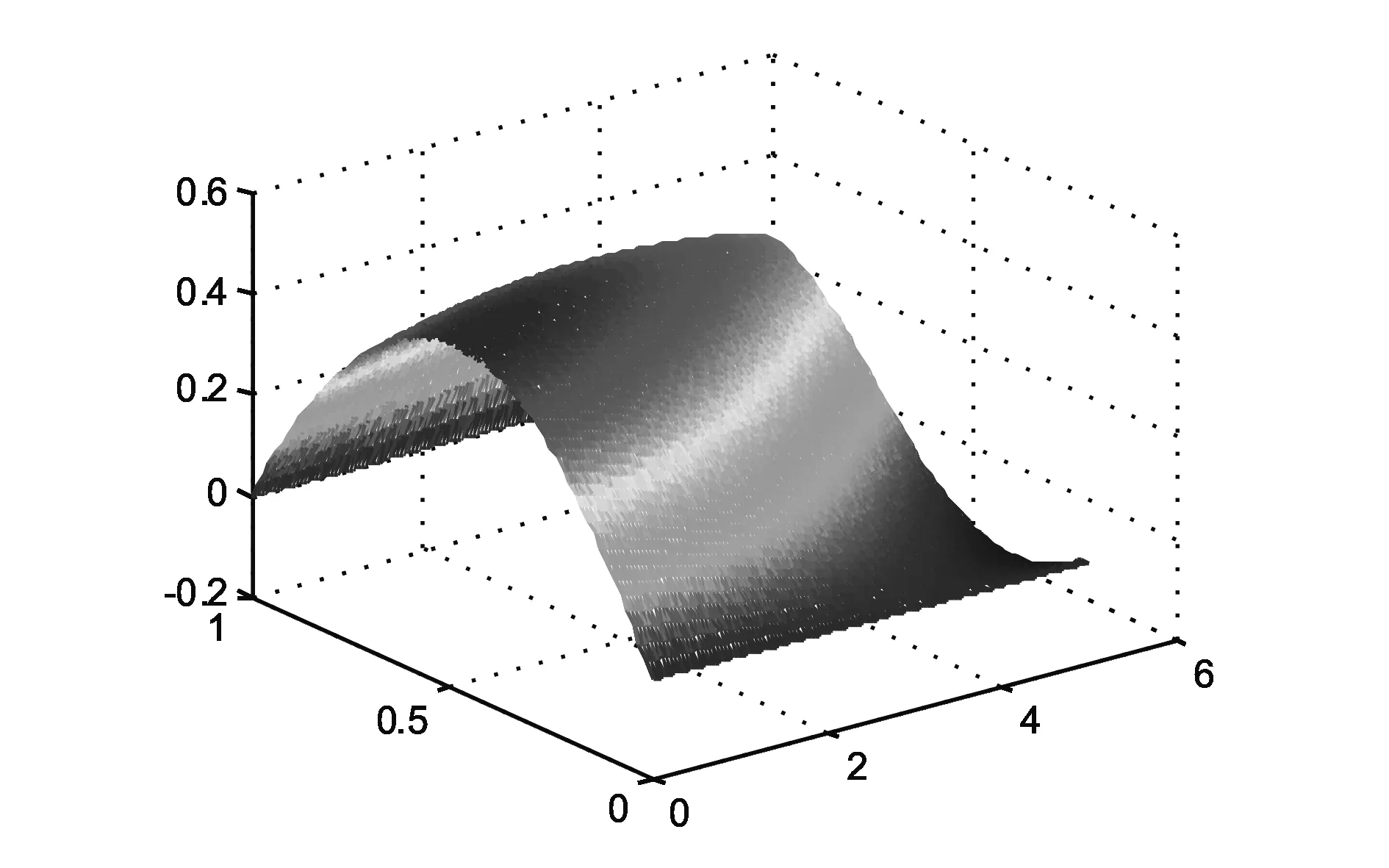
图1 α=0.000 1,β=2.5时BBMB方程的近似解

图2 α=0.01,β=25时BBMB方程的近似解
通过例1和例2可知,本文提出的方法不仅适合求解BBMB方程的近似解,而且也适合于求解其他方程的近似解.
参考文献:
[1]Benjamin T B,Mahony J J. Model equations for long waves in nonlinear dispersive systems[J]. Philosophical Transactions of the Royal Society of London,1972,272:47-78.
[2]Korteweg D J,de Vries G. On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves[J]. Philosophical Magazine,1895,39:422-433.
[3]Ewing R E. Time-stepping Galerkin methods for nonlinear Sobolev partial differential equation[J]. SIAM Journal on Numerical Analysis,1978,15:1125-1150.
[4]Omrani K. The convergence of the fully discrete Galerkin approximations for the Benjamin-Bona-Mahony(BBM)equation[J]. Appl Math Comput,2006,180:614-621.
[5]Raupp M A. Galerkin methods applied to the Benjamin-Bona-Mahony equation[J]. Boletim da Sociedade Brazilian Mathematical,1975,6:65-77.
[6]Wahlbin L. Error estimates for a Galerkin methods for a class of model equations for long waves[J]. Numerische Mathematic,1975,23:289-303.
[7]Achouri T,Khiari N,Omrani K. On the convergence of difference schemes for the Benjamin-Bona-Mahony(BBM)equation[J]. Appl Math Comput,2006,182:999-1005.
[8]Kannan R,Chung S K. Finite difference aapproximate solutions for the two-dimensional Burgers system[J]. Comput Math Appl,2002,44:194-200.
[9]Omrani K,Ayadi M. Finite difference discretization of the Benjamin-Bona-Mahony(BBM)equation[J]. Numer Meth Part Differ Equat,2008,24:239-248.
[10]Al-Khaled K,Momani S,Alawneh A. Approximate wave solutions for generalized Benjamin-Bona-Mahony(BBMB)equations[J]. Appl Math Comput,2005,171:281-292.
[11]Kaya D. A numerial simulation of solitary-wave solutions of the generalized regularized long-wave equation[J]. Appl Math Comput,2004,149:833-841.
[12]Aksan E N. Quadratic B-spline finite element method for numerical solution of the Burgers equation[J]. Appl Math Comput,2006,174:884-896.
[14]Zarebnia M,Parvaz R. Cubic B-spline collocation method for numerical solution of the Benjamin-Bona-Mahony(BBMB)equation[J]. International Journal of Mathematical Sciences,2013,7:34-37.
