A Property of Convex Mappings on the Classical Domains

FENG Shu-xia,LI Hong-jun

(Institute of Contemporary Mathematics,College of Mathematics and Information Science,Henan University,Kaifeng 475004,China)

A Property of Convex Mappings on the Classical Domains

FENG Shu-xia,LI Hong-jun

(Institute of Contemporary Mathematics,College of Mathematics and Information Science,Henan University,Kaifeng 475004,China)

In this paper,we give a property of normalized biholomorphic convex mappings on the f i rst,second and third classical domains:for any Z0belongs to the classical domains, f maps each neighbourhood with the center Z0,which is contained in the classical domains, to a convex domain.

classical domains;convex mappings;convex domains

§1.Introduction

Convex mappings play an important role in several complex variables geometric function theory,so far there are many beautiful results for them[1].In 1936,Robertson M S[2]has proved that a convex function which is def i ned on the unit disk D={z∈ℂ:|z|＜1}can map each small disk contained in D to a convex domain.In 1989,Brow J E[3]obtained the result again. Then,is this result true for convex mappings on the unit ball Bn={z=(z1,z2,···,zn)0∈Unfortunately,we don’t know the result for general convex mappings.But for a special class of convex mappings,Feng Shu-xia has proved that it is correct.

Theorem A[4]Suppose then f(z)is a normalized biholomorphic convex mapping,and f(Bn(z0,r))is a convex domain in ℂn,for∀z0∈Bn,r∈(0,1−‖z0‖].p∈∂Bn,where z,p are column vectors,

It is naturally to consider whether it is true for convex mappings on more general domains. It is well known that Professor Hua Luo-keng[5]has given the matrix representation for the four classical domains

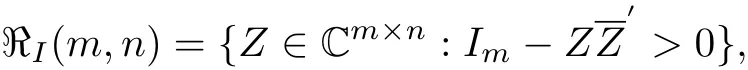
where 1≤m≤n,“＞”means positive def i ned.ℜI(m,n)is called the f i rst classical domain.

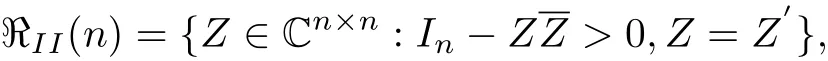
where n≥1.ℜII(n)is called the second classical domain.

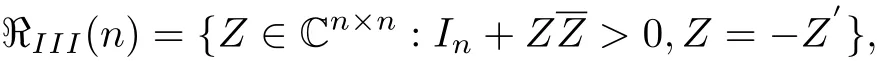
where n≥2.ℜIII(n)is called the thired classical domain.

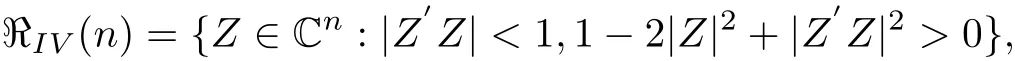
where n≥3.ℜIV(n)is called the fourth classical domain.

In this paper,we discuss the same property of convex mappings on three classical domainsℜI(m,n),ℜII(n)and ℜIII(n).

Professor Liu Tai-shun[6]has given the Minkowski functional for the classical domains as follows

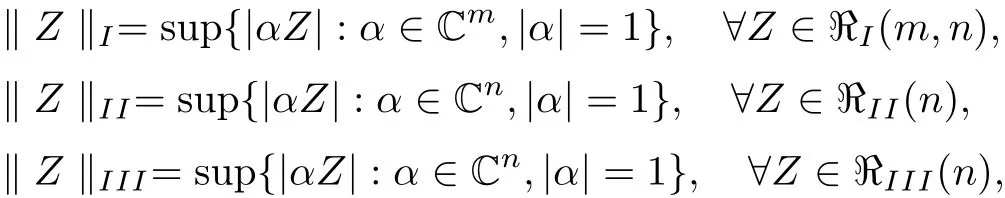
where α is a row vector.

§2.Main Results

It is well known that Mok Ngaiming and Tsai I-Hsun[7]have completely characterized convex mappings in irreducible homogenous Hermitian symmetric space of rank≥2.

Lemma 2.1[7]Let X0be an irreducible Hermitian symmetric manifold of noncompact type and of rank≥2 and τ:X0−→Ω0⊂⊂ℂNbe the Harish-Chandra embedding.Let D0be a bounded convex domain in ℂNand f:X0−→D0be a biholomorphism.Then f is the Harish-Chandra embedding up to automorphisms of X0and affine linear transformations ofℂN.More precisely,f is of the form T◦τ◦ϕ,where T is an affine linear transformation of ℂNand ϕ is an automorphism of X0.

The generalization of the above theorem to unbounded convex realizations is also proved.

By Lemma 2.1,the normalized biholomorphic convex mappings on the f i rst classical domainℜI(m,n)must be[1]

where P∈ℜI(m,n).

Lemma 2.2Suppose f(Z)is a normalized biholomorphic convex mapping on ℜI(m,n), then for∀Z,W∈ℜI(m,n),0≤t≤1,we have

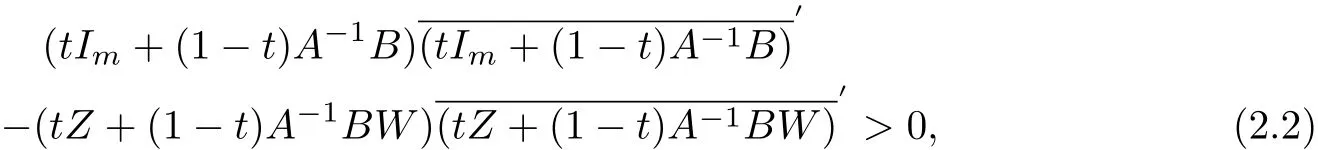
ProofSince f(Z)is a normalized biholomorphic convex mapping on ℜI(m,n),then f(Z)= Z(In−)−1,where P∈ℜI(m,n)and for∀Z,W∈(m,n),0≤t≤1,

therefore

By easy computation we can get

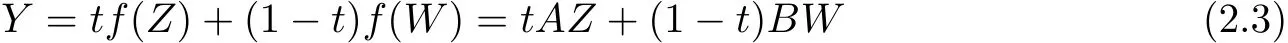
and

Consequently

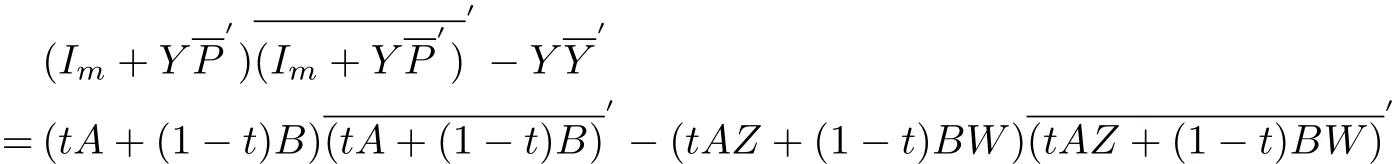
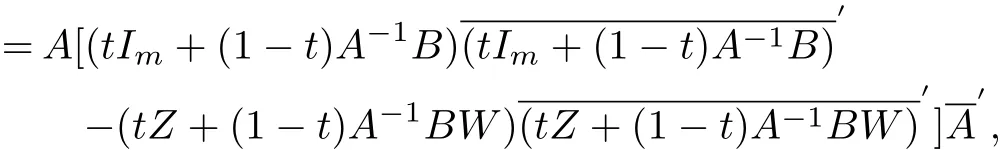
hence

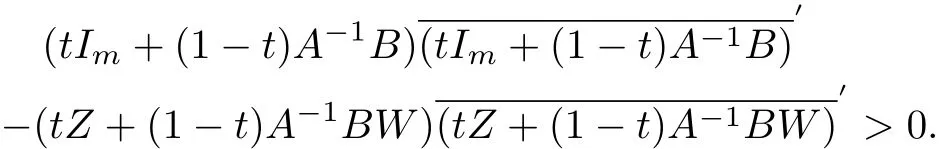
Theorem 2.1Suppose f(Z)is a normalized biholomorphic convex mapping on ℜI(m,n), then for∀Z0∈ℜI(m,n),0＜r≤1−‖Z0‖I,f(Ω(Z0,r))is a convex domain,where Ω(Z0,r)=

ProofSince f(Z)is a normalized biholomorphic convex mapping on ℜI(m,n),then f(Z)=

In order to obtain f(Ω(Z0,r))is a convex domain,we only need to prove that there exists a point X∈Ω(Z0,r)satisfying f(X)=tf(Z)+(1−t)f(W)∈f(Ω(Z0,r)),for∀Z,W∈Ω(Z0,r),0≤t≤1.

In the following,we will prove

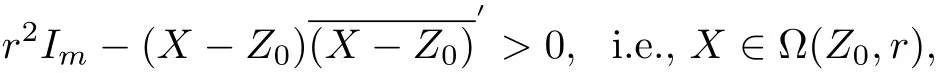
Using(2.3)and(2.4)in Lemma 2.2,we have

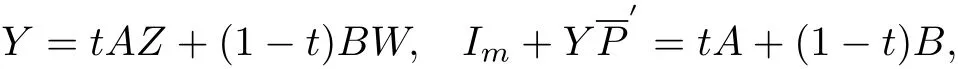
then

hence it is only need to prove

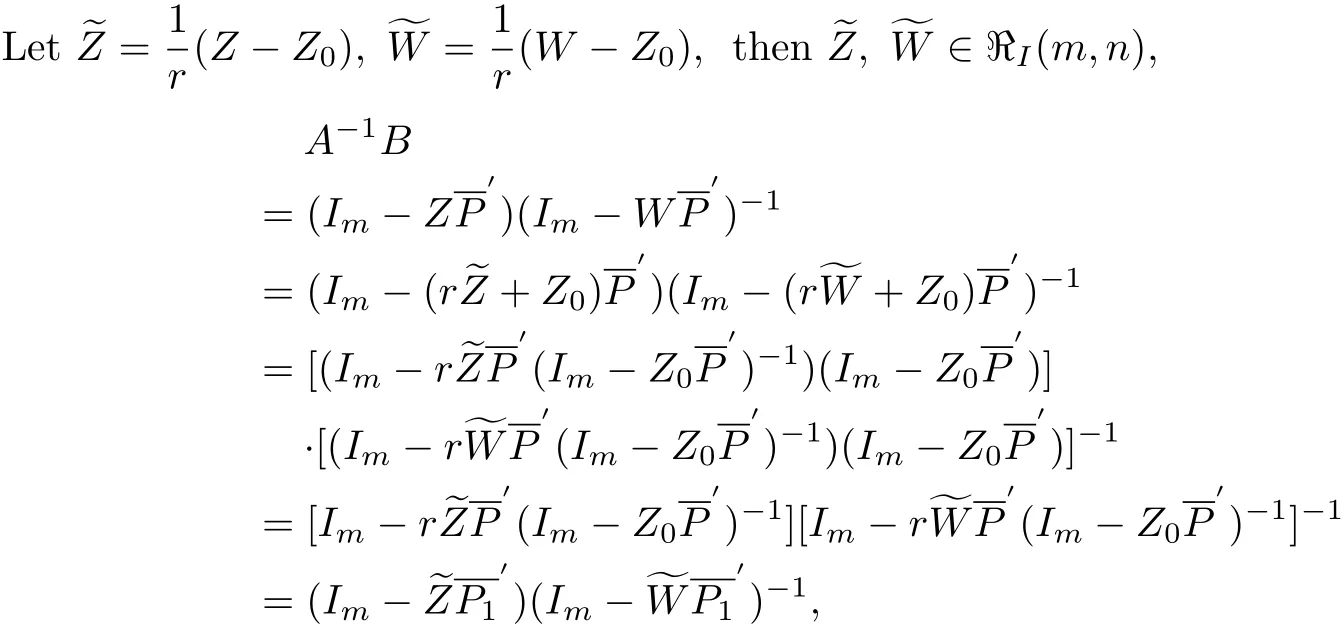
where P1=r(Im−P,and(2.5)becomes

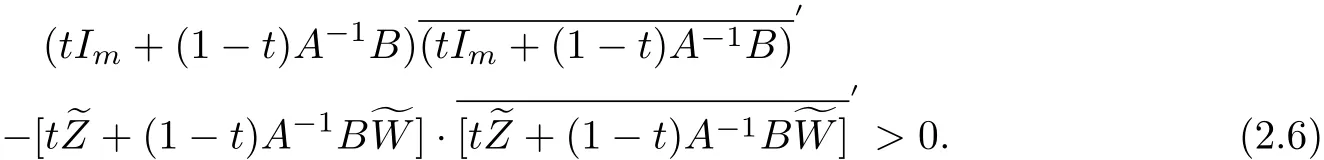
Since

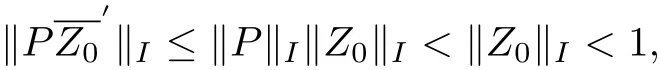
we can get

so

i.e.,P1∈ℜI(m,n).

By(2.1),we know that f1(Z)= is also a normalized biholomorphic convex mapping on ℜI(m,n).Then we can get(2.6)by Lemma 2.2 and theorem is proved.

Similar to Theorem 2.1,we can obtain the following two theorems on ℜII(n)and ℜIII(n).

Theorem 2.2Suppose f(Z)is a normalized biholomorphic convex mapping on ℜII(n), then for∀Z0∈ℜII(n),0＜r≤1−‖Z0‖II,f(Ω(Z0,r))is a convex domain,where

Theorem 2.3Suppose f(Z)is a normalized biholomorphic convex mapping on ℜIII(n), then for∀Z0∈ℜIII(n),0＜r≤1−‖Z0‖III,f(Ω(Z0,r))is a convex domain,where

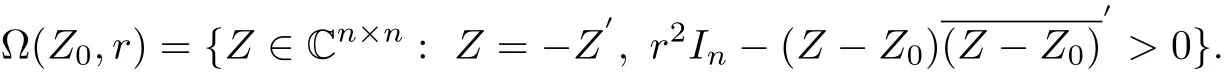
For the fourth classical domain,we haven’t get any result for convex mapping.So the readers can do some work on it.

[1]GONG Sheng.Convex and Starlike Mappings in Several Complex Variables[M].Dordrecht:Kluwer Academic Publishers,1998.

[2]ROBERTSON M S.On the theory of univalent functions[J].Ann of Math,1936,37:374-408.

[3]BROW J E.Images of disks under convex and starlike functions[J].Math Z,1989,202:457-462.

[4]FENG Shu-xia.Some Classes of Holomorphic Mappings in Several Complex Variables[D].Hefei:Univ Sci Tech China,2004.

[5]HUA Luo-keng.Harmonic Analysis of Functions of Several Complex Variables in the Classical Domains[M]. Beijing:Science Press,1958.

[6]LIU Tai-shun.The Growth Theorems,Covering Theorems and Distortion Theorems for Biholomorphic Mappings in Several Complex Variables[D].Hefei:Univ Sci Tech China,1989.

[7]MOK Ngaiming,TSAI I-Hsun.Rigidity of convex realizations of irreducible bounded symmetric domains of rank≥2[J].Journal f¨uv die reine und angewandte Mathematik,1992,431:91-122.

tion:32H02,32A30,30C45

CLC number:O174.56Document code:A

1002–0462(2014)02–0292–06

date:2013-05-16

Supported by the National Natural Science Foundation of China(11001074,11061015, 11101124)

Biographies:FENG Shu-xia(1975-),female,native of Yuanyang,Henan,an associate professor of Henan University,Ph.D.,engages in function theory of SCV;LI Hong-jun(1986-),male,native of Fugou,Henan,a graduate student of Henan University.