m-degree Center-connecting Line of Finite Points Set and Its Properties

ZHOU Yong-guo

(The No.1 Middle School,Yuanling Country,Huaihua 419600,China)

m-degree Center-connecting Line of Finite Points Set and Its Properties

ZHOU Yong-guo

(The No.1 Middle School,Yuanling Country,Huaihua 419600,China)

In this paper,we f i rst give the concept of m-degree center-connecting line in n-dimensional Euclidean space Enand investigate its several properties,then we obtain the length of m-degree center-connecting line formula in f i nite points set.As its application, we extend the Leibniz formula and length of medians formula in n-dimensional simplex to polytope.

n-dimensional Euclidean space;f i nite points set;m-degree center-connecting line;properties

§1.Def i nition and Notation

Conventions for this paper,let Endenote an n-dimensional Euclidean space,Ω(N)denote a set of f i nite points in En,that is,

be a fi nite points set in En.Let{A1,A2,···,AN}=,Ωj(m)be a fi nite points set which is constitued by arbitrary m points·,Amin Ω(N)and Ωj(m)be the set which is constitued by the remaining N−m p

In 1980,professor Yang Lu and professor Zhang Jingzhong[1]had conducted pioneering work on fi nite points set in Enand their work received extensive attention[2-6].In this paper, we apply the analytical method,establish the notion of m-degree center-connecting line of a fi nite points set,and discuss its properties,obtain the length of m-degree center-connecting line formula.As its application,we extend the Leibniz formula[7]111and length of medians formula[8]in n-dimensional simplex to polytope[9].

De fi nition 1Establish a rectangular coordinate system in En,suppose that

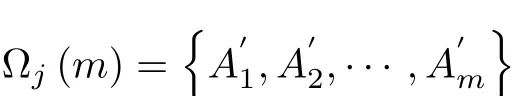
and

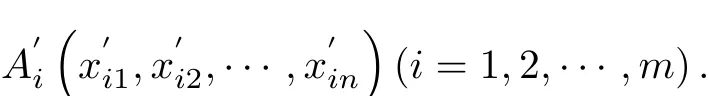
For k＞0,let

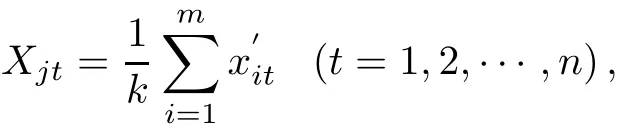
then we call Gjk(Xj1,Xj2,···,Xjn)the No.k center of Ωj(m).

According to Def i nition 1,

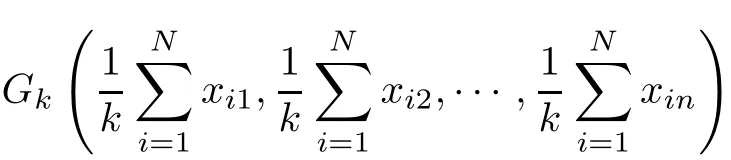
is the No.k center of the f i nite points set Ω(N),

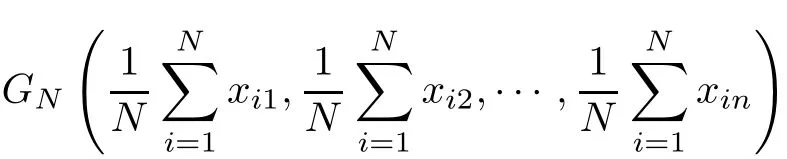
is the centroid of the f i nite points set Ω(N).

In particular,Gkis also the No.k center of polytope

in En.

Def i nition 2Suppose that Gjk1is the No.k1center of set Ωj(m)and Gjk2is the No.k2center of set Ωj(m)?m∈ℕ,1≤m≤?,then we call segment Gjk1Gjk2the m-degree centerconnecting line of f i nite points set Ω(N).

Obviously,f i nite points set Ω(N)have and only have CmNm-degree center-connecting lines (including m-degree center-connecting lines which coincide with each other).We easily know that median of n-dimensional simplex[7]110,median of polygon and the k-degree median of polygon are special cases of the m-degree center-connecting line of f i nite points set Ω(N).

§2.Main Results and Proofs

ProofSuppose that Gjk1Gjk2is an arbitrary m-degree center-connecting line of Ω(N)(1≤j≤),we take its inner divided point P so that

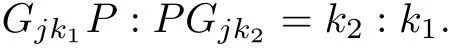
Obviously,we just need to prove that P is the No.(k1+k2)center of Ω(N).

Establish a rectangular coordinate system in En.Inthe setΩ(N)={A1,A2,···,AN}, suppose that

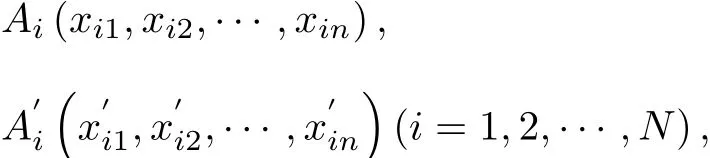
from the Def i nition 1,Gjk1(Xj1,Xj2,···,Xjn),the No.k1center of Ωj(m),satisf i es

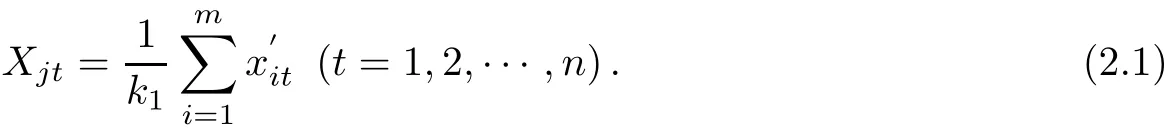
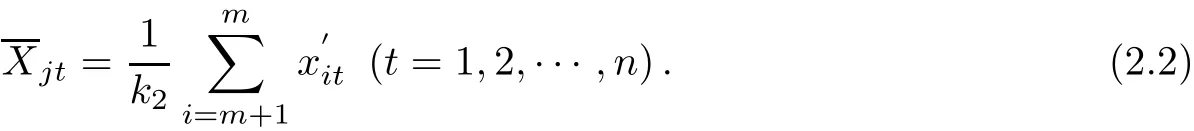
Suppose that P(x1,x2,···,xn),according to the formula of Def i nite Proportionate Inserted Point[7]121,

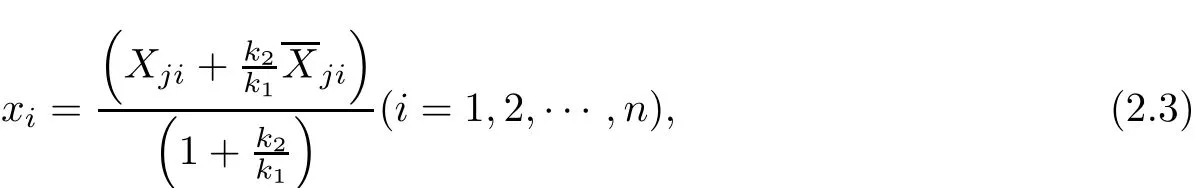
take(2.1)and(2.2)into(2.3),we have

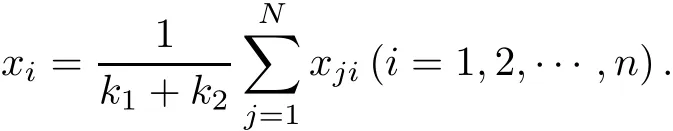
therefore,P is the No.(k1+k2)center of Ω(N).Theorem 1 is proved.

Theorem 2In f i nite points set Ω(N),for an arbitrary point P in En,we have

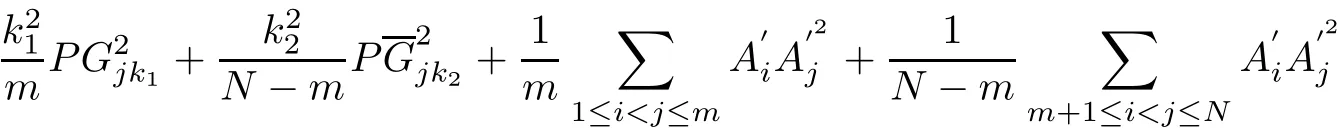
ProofEstablish a rectangular coordinate system in En,take P as the origin.In the setΩ(N)={A1,A2,···,AN},suppose that

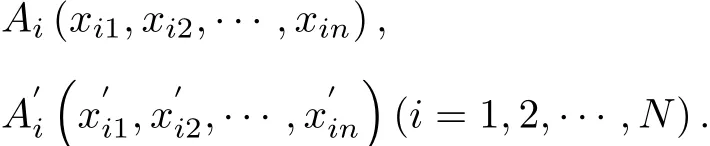
By Def i nition 1,Gjk1(Xj1,Xj2,···,Xjn),the No.k1center of Ωj(m),satisf i es(2.1),Gjk2(Xj1, Xj2,···,Xjn),the No.k2center of Ωj(m),satisf i es(2.2).Then

and

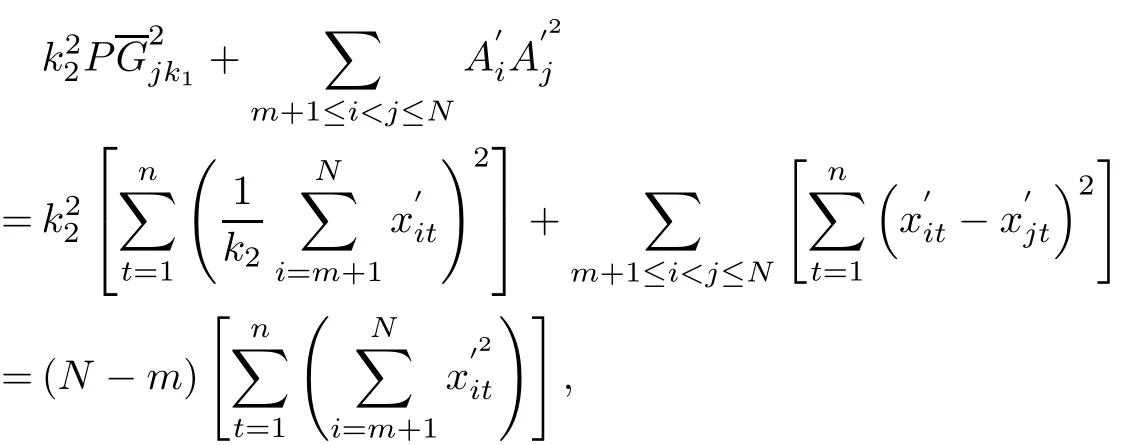
hence

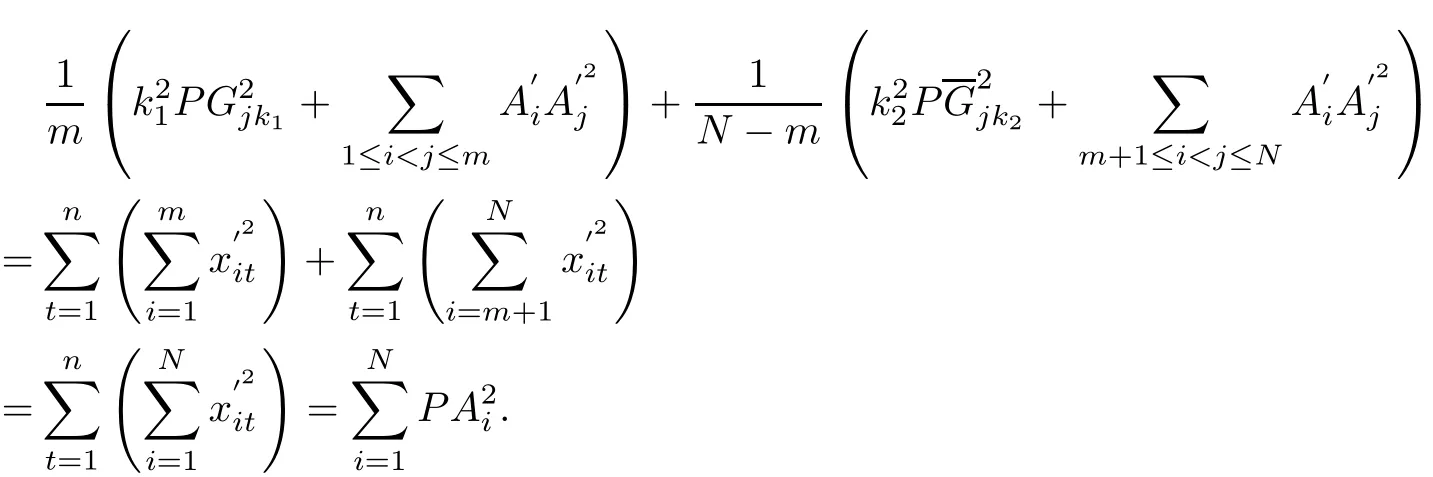
The equality(2.4)follows immediately.The proof is completed.

In Theorem 2,choose Ωj(m)=Ωj(1)={AN},k1=1,k2=k and replace N by N−1, then we have

Corollary 1Suppose that Gkis the No.k center of polytope Φ(N)={A1,A2,···,AN}(N≥n+1)in En,for an arbitrary point P in En,we have

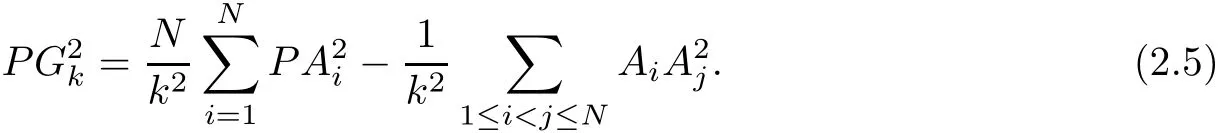
In Corollary 1,take k=N,that is,GNis the centroid of polytope Φ(N),we have

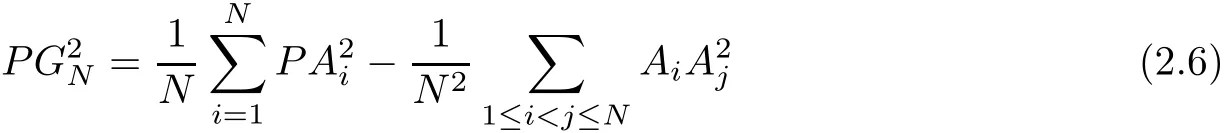
furthermore,we have

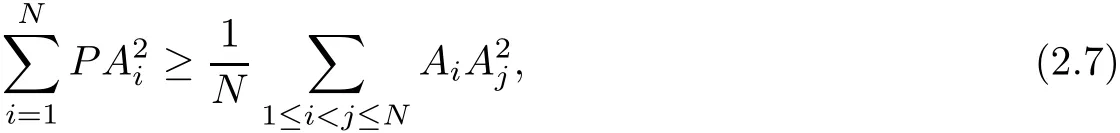
where equality holds if and only if P is the centroid of polytope Φ(N),that is,P=GN.

(2.6)can extend Leibniz formula from n-dimensional simplex to polytope.

Corollary 2The sum of squares of the distance from the point to each vertex of polytope is a constant,then the trace of the point is a hypersphere whose center is the No.k center of polytope.

Theorem 3In f i nite points set Ω(N),we have

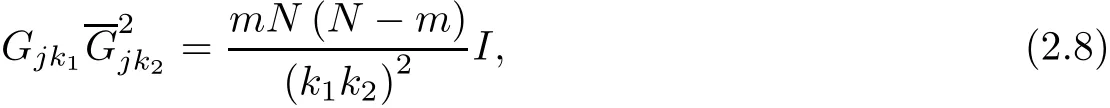
in which

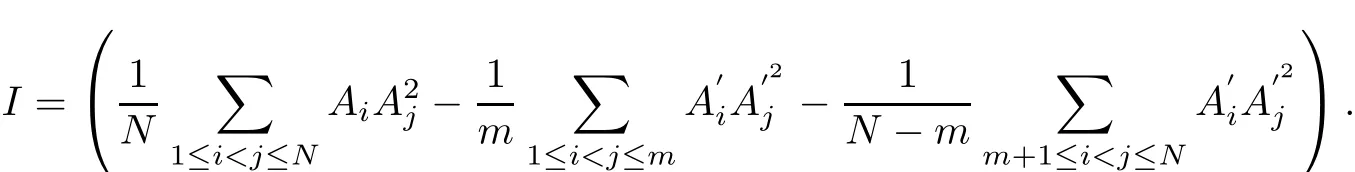
ProofSuppose that M is the No.(k1+k2)center of Ω(N),by Theorem 1,we can get MGjk1:MGjk2=k2:k1and therefore

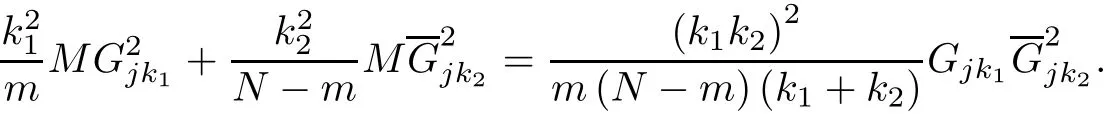
It is easy to know that(2.6)is also available in f i nite points set Ω(N).Consequently,in(2.6), take P=M,k=k1+k2,we can obtain that N

In Theorem 2,take P=M,we can get(2.8)from the above two formulas and Theorem 2. The proof is completed.

(2.8)can be considered as the length of m-degree center-connecting lines formula in f i nite points set Ω(N).

In Theorem 3,take

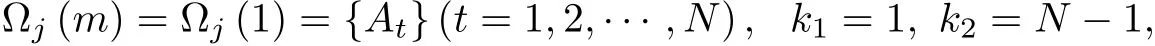
we get

Corollary 3In polytope Φ(N)={A1,A2,···,AN}(N≥n+1),let GtN−1denote the centroid of polytope which is constitued by the points

take A0=AN,AN+1=A1,then

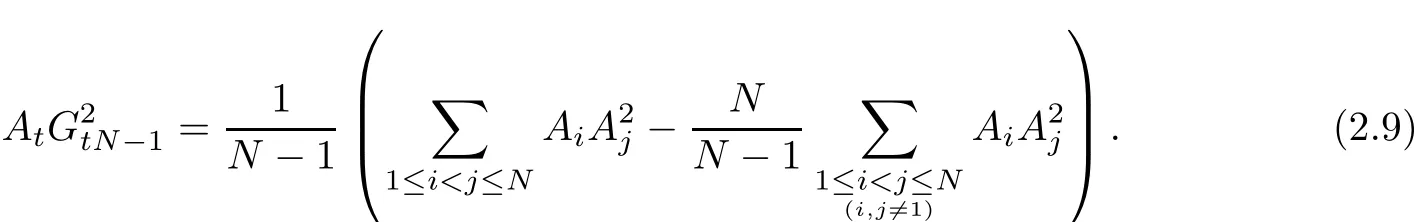
In(2.9),let N=n+1,we obtain the length of medians formula in n-dimensional simplex. Therefore,(2.9)can be considered as the length of medians formula in polytope.

Remark[8]and[10]are special cases of this paper.

AcknowledgementThe author would like to acknowledge the support from Professor Leng Gangsong.

[1]YANG Lu,ZHANG Jing-zhong.A class of geometric inequalities on f i nite points[J].Acta Math Sinica, 1980,23(5):740-749

[2]YANG Lu,ZHANG Jing-zhong.A class of geometric inequality concerning a mass-point system[J].J China Univ Sci Technol,1981,11(2):1-8.

[3]YANG Lu,ZHANG Jing-zhong.Pseudo symmetric sets and related geometric inequalities[J].Acta Math Sinica,1986,29(6):802-806.

[4]ZHOU Jia-nong.Total ball-point an inequality between the distance of each other[J].Chinese Science Bulletin,1988,(14):1045-1047.

[5]YANG Shi-guo.Two theorems on f i nite pointsset[J].Journalof Southwest China Teachers University(Natural Science),1991,17(3):295-298.

[6]SU Hua-ming.A class of geometric inequalities on total ball f i nite points set[J].Chinese Journal of Contemporary Mathematics,1994,15A(1):46-49.

[7]SHEN Wen-xuan.Simplex Theory Guide[M].Hunan:Hunan Normal University Press,2000.

[8]ZHANG Yao.Two geometric inequalities concerning lengths of medians of a simplex[J].Journal of Hunan Educational Institute,1994,12(5):99-103.

[9]ZHANG Yao.A class of inequalities concerning the polytope[J].Journal of Hunan Educational Institute, 1999,17(5):99-105.

[10]ZHOU Yong-guo.Several properties of k-degree midline of polygon[J].Bulletin of Mathematics,2005,(15): 26-27.

tion:51M16,52B11

CLC number:O123.2Document code:A

1002–0462(2014)02–0247–06

date:2012-09-20

Supported by the Department of Education Science Research Project of Hunan Province (09C470)

Biography:ZHOU Yong-guo(1962-),male,native of Yuanling,Hunan,a senior teacher of Yuanling No.1 Middle School,engages in elementary mathematics and high-dimensional convex bodies geometry.