螺栓拉应力超声无损检测方法
2014-07-30徐春广李潘勤学宋文涛
徐春广李 骁 潘勤学 宋文涛
(北京理工大学 机械与车辆学院 北京 100081)
1 引言
螺栓作为工业现场中常用的连接件,普遍存在于航空航天、船舶轮机、桥梁建设、化工设备、新能源等领域关键设备的连接处,起强化、密封的重要作用。其中,螺栓轴向应力作为影响螺栓性能、寿命以及使用状态的重要因素,愈发受到重视。由于栓体结构的特殊性以及轴向加载后螺纹部分的形变,给螺栓轴向应力测量带来了非常大的不确定性以及测量难度,近几十年来国内外都在积极地探索解决这一问题的办法[1]。目前,工业现场常用到扭力扳手来简易确定螺栓轴向应力值大小。但由于螺帽部分与螺纹摩擦副部分的反向扭矩影响以及螺栓螺纹副部分的弹性变形,真正能够使螺栓产生轴向应力的扭矩不到扭力扳手面板数值的20%[2]。除此以外,采用脉冲回波反射法、渡越时间法、相位法等技术的超声纵波螺栓轴向应力的无损检测技术也能够有效的获取螺栓轴向应力值大小,但针对已安装螺栓或埋深地脚螺栓等原长度未知的栓体轴向应力测量则无能为力[3-4]。针对超声波无损检测技术需要稳定耦合这一缺点提出的采用电磁超声激励剪切波测量螺栓轴向预紧力的办法,也取得了一定的研究成果,但依然没有解决螺栓轴向长度未知情况下轴向应力大小的测量问题[5]。根据声弹性理论,超声波在各向均一金属材料中的传播速度与应力值大小有一定的对应关系,且可以通过横波与纵波表达式联立求解的方式,消除螺栓轴向长度以及温度变化带来的影响[6]。但是在实际测量中,螺栓轴向应力在低载荷与高载荷情况下,声时差之比并不与应力值大小呈单纯的线性关系。因此,需要探索一种更为有效的应力测量模式,从而更准确地获得螺栓轴向应力值大小,解决这一急需的工业应用难题。
2 螺栓轴向应力测量基本原理
根据声弹性理论的基本假设,超声波在各向均一介质中传播的速度方向、偏振方向与应力作用方向之间有如下关系[7]:

其中,Vijk中i表示波的传播方向,j表示波的偏振方向,k表示单轴应力的作用方向,ρ0为材料密度,λ,μ为材料的二阶弹性常数,l,m,n为材料的三阶弹性常数。
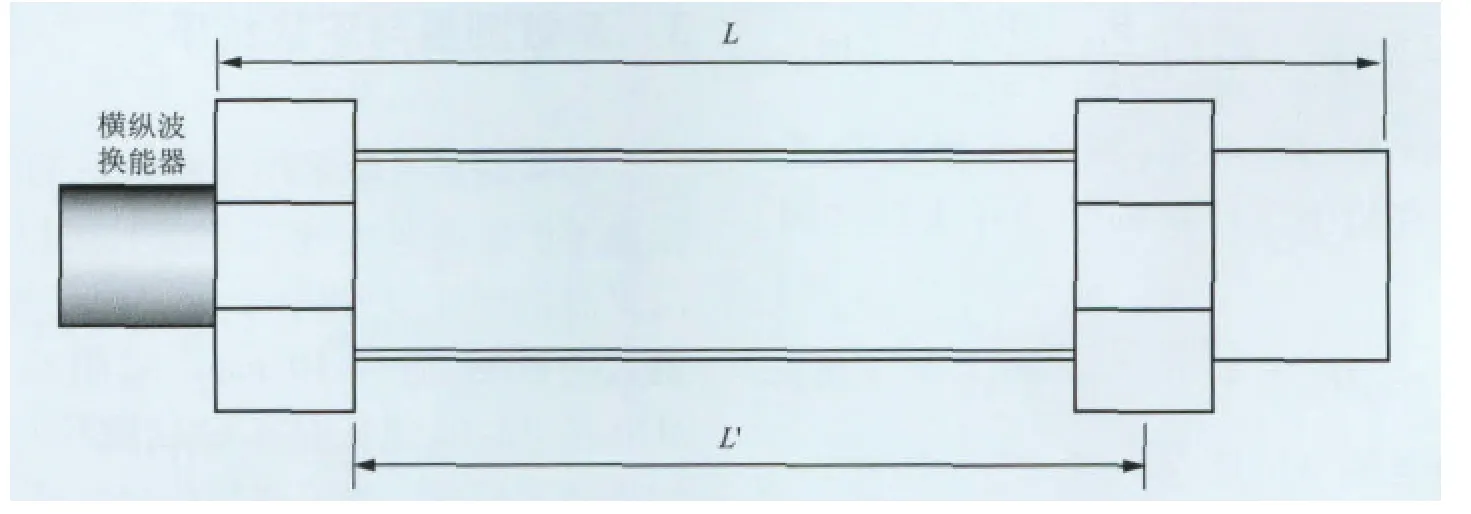
图1 螺栓轴向应力测量物理模型Fig.1 Physicalmodel of bolt axial stressmeasurement
根据弹性力学基本假设,在轴向应力小于螺栓材料的屈服极限之前,可以认为螺栓钢为完全弹性体。那么,当测量温度恒定(室温)状态下,螺栓材料的二阶、三阶弹性常数不会随着轴向应力的增加而变化。因此,影响螺栓轴向应力测量的因素只有螺栓长度与测量温度。考虑到螺母旋紧后有效应力作用区并不是螺栓副包裹的全部区域,如图1,建立紧固螺栓轴向应力测量的物理模型[8-9]。通过在螺栓头部放置横纵波换能器,采用脉冲反射回波法测量横纵波在螺杆中的渡越时间,间接计算螺栓轴向应力大小。
图1中,L为螺栓全长,L'为拉应力作用区域(室温,20℃)。
考虑到测量温度对于螺栓整体线性膨胀的影响以及弹性变形对于螺栓应力作用区长度的影响,螺栓长度计算公式可作如下表达:
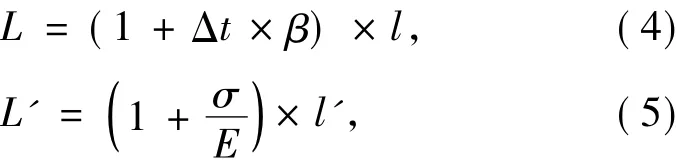

式中,l,l'分别表示温度影响前的螺栓全长,以及应力作用前应力影响区长度,t,t0分别表示当前温度与标准温度(20℃室温),β,E分别表示线性温度膨胀系数与杨氏模量。将公式(3)、(4)、(5)带入公式(1)、(2),则螺栓轴向应力与横波、纵波传播速度的关系可表示为
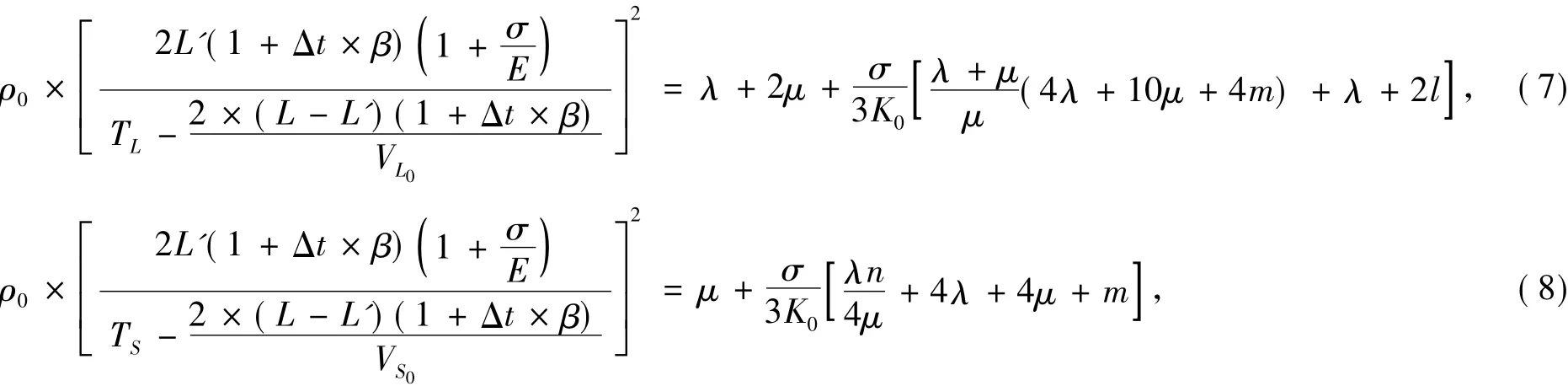
式中,TL,TS分别为最终测量的纵波与横波的度越时间,VL0,VS0分别表示无应力状态下超声纵波与横波的波速,VLσ,VSσ分别表示对应σ应力状态下的超声纵波波速与横波波速。
令

考虑到实际测量横波与纵波的渡越时间很短,温度的变化可忽略为零,则Δt=0。将公式(7)、(8)两式相除,则原方程可化简为
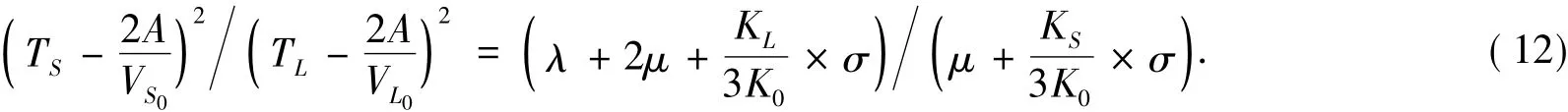
令
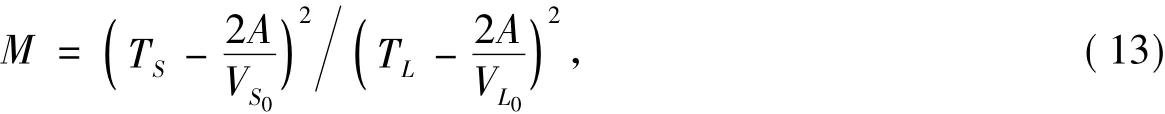
则应力最终表达式为
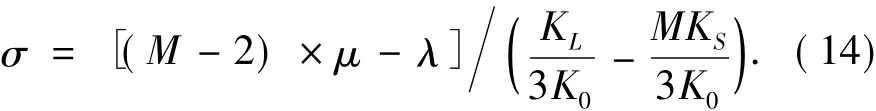
由于公式中 KL,KS未知,那么可根据公式(15),通过在拉伸机上进行拉伸试验并求得这两个系数:

为了便于计算测量结果,令
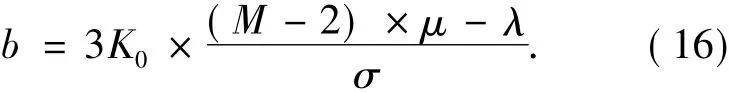
3 系数测量与实验结果
实验测量系统采用对称设计的横纵波换能器,换能器横纵波单元相互独立且可以同时激励横波与纵波信号,中心频率2.25 MHz,为宽频窄脉冲接触式换能器,直径10 mm。被测栓体为公称直径M20的A2-70奥氏体不锈钢螺栓与强度等级4.8的低碳钢螺栓。为了取得稳定的耦合效果,螺栓螺帽与尾部均进行了铣削平整化处理,试验温度控制在26℃。
本系统采用脉冲收发仪进行超声波信号激励,利用示波器精确记录横纵波渡越时间。通过在拉伸机进行精确地定量拉伸试验,可以获得准确地应力-声时对应曲线图。由于低碳钢螺栓最大屈服强度为320 MPa,螺栓轴向拉伸试验应力设定范围为0~300 MPa,以25 MPa为一个步进进行拉伸试验,实验结果如图2、图3所示。
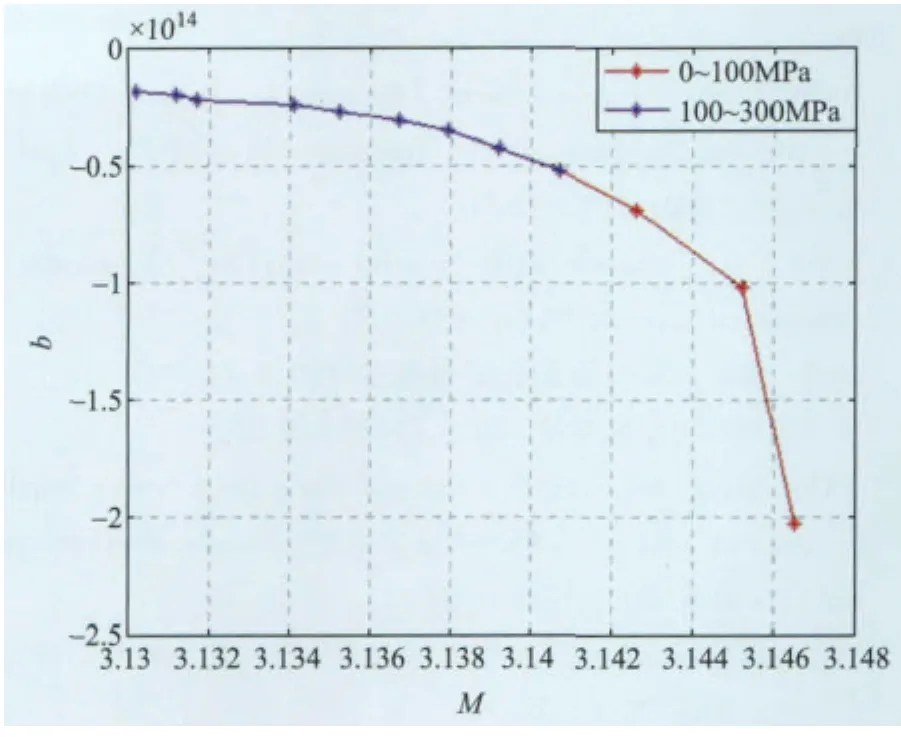
图2 A2-70螺栓M-b拟合曲线图Fig.2 Fitting curve M-b of A2-70 bolt
从图2、3中我们可以看出,两种不同材质螺栓在低应力载荷的条件下,M-b曲线并不是单纯的线性关系,这主要是由于螺栓的螺纹副在0~100 MPa的应力条件下,最先发生的是螺纹副的夹紧、摩擦与弹性变形,进而才进入弹性变形阶段(100~300 MPa)。由此,我们可将KL,KS的数值按照不同载荷情况分别进行拟合,如表1。
根据表1中拟合结果,可以做出理论应力值与实测应力值大小分布,如图4、5所示。

表1 KL,KS拟合结果Table 1 Fitting results of KL,KS
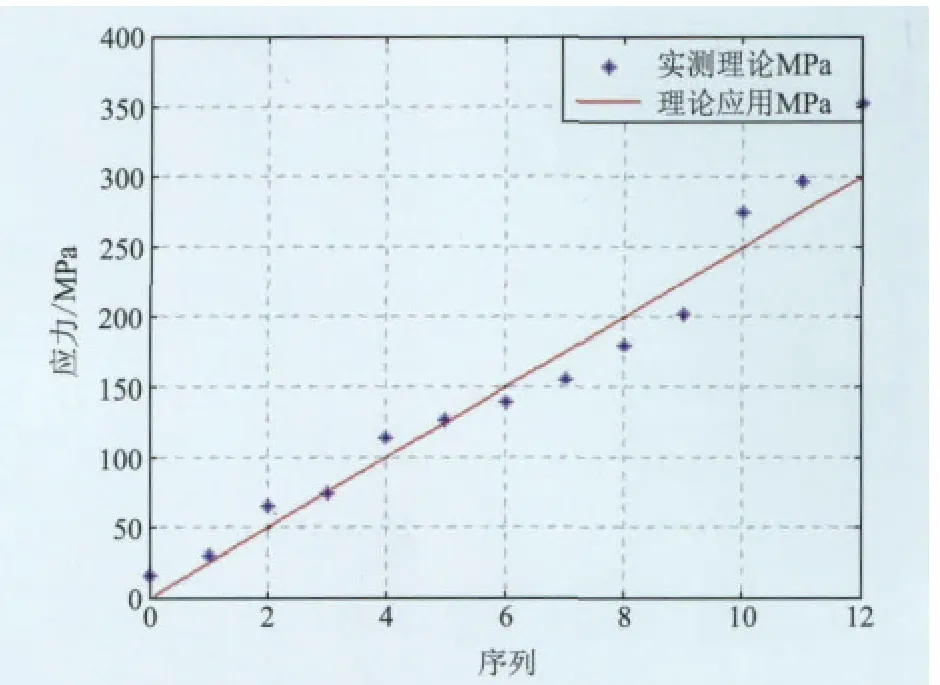
图4 A2-70螺栓理论应力值与实测应力值对比分布图Fig.4 The comparison result of A2-70 bolt
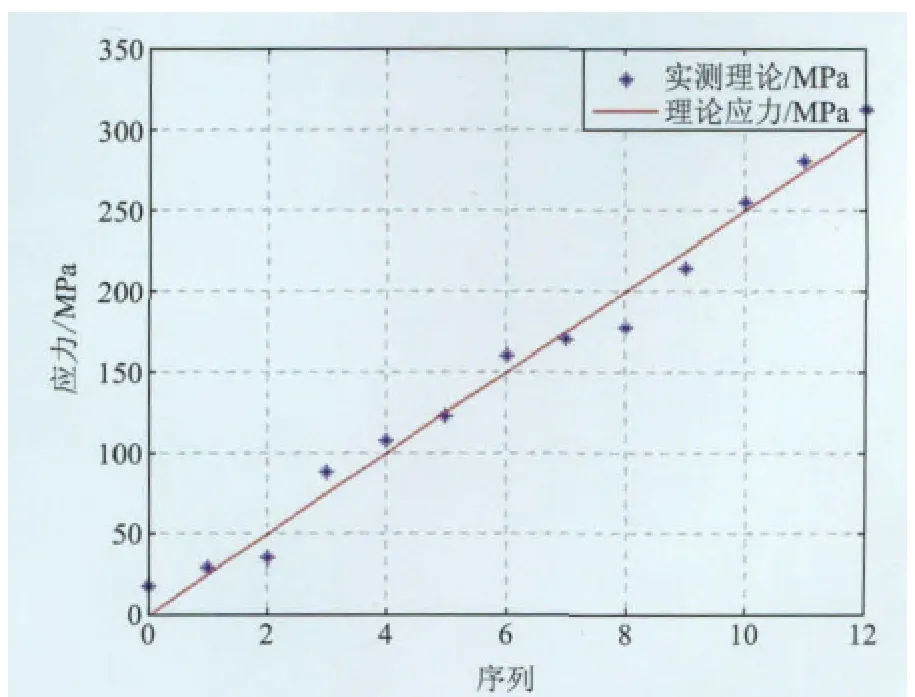
图5 4.8螺栓理论应力值与实测应力值对比分布图Fig.5 The comparison result of4.8 bolt
4 结论
本文通过横纵波结合的办法,提出了一套快速有效测量螺栓轴向应力的测量方法,在测量过程中,温度与弹性变形导致的螺栓长度变化造成的影响均可以得到消除,且螺栓轴向长度未知的情况下,栓体轴向应力值也能够得到测量。除此以外,本文还对低载荷与高载荷不同应力状态下的螺栓轴向应力测量系数进行了分类探讨,提出了更准确的测量螺栓轴向应力的计算办法,使得螺栓轴向应力测量实际结果与理论值平均误差小于2.9367%,可以广泛的应用于航空航天、船舶轮机、桥梁建设、化工设备、新能源等领域中螺栓轴向应力测量的工业现场测量环境。
[1]李光.螺栓轴向应力测量技术的研究概况及展望[J].南通大学学报(自然科学版),2009,8(3):67-71.LIGuang.Research and prospect on the technique for bolt axial stressmeasurement[J].Journal of Nantong University(Natural Science Edition),2009,8(3):67-71.
[2]滕冠.高强度螺栓的紧固分析[J].装备制造技术,2009(4):163-165,171.TENG Guan.Analysis of high-strength fasteners fastening[J].2009(4):163-165,171.
[3]杜刚民.螺栓轴向应力超声测量技术[J].无损检测,2006,28(1):20-22,25.DU Gangmin.Bolt axial stressmeasurement by ultrasonic testing[J].Nondestructive Testing,2006,28(1):20-22,25.
[4]JHANG K Y.Estimation of clamping force in high-tension bolts through ultrasonic velocity measurement[J].Ultrasonics.2006 44:e1339-e1342.
[5]JHANG K Y.Contactlessmeasurement of bolt axial stress using a shear-wave electromagnetic acoustic transducer M.Hirao [J].NDT&E international,2001,34:179-183.
[6]江泽涛.纵横波测已紧固螺栓轴向应力[J].应用声学,2000,19(1):16-21.JIANG Zetao.Themeasurementof the stress in a tightened boltby the ultrasonic longitudinal and transverse waves [J].Appl.Acoustic,2000,19(1):16-21.
[7]ROSE J L.Ultrasonic waves in solid media[M].Cambridge:Cambridge University Press,1999.
[8]杨强.螺母牙形及旋合长度对螺栓牙根部应力的影响[J].天津工程师范学院学报,2007,17(3):29-32.YANG Qiang.Influence of nut thread shape and screwing length on bolt root stress[J].Journal of Tianjin university of technology and education,2007,17(3):29-32.
[9]金晶.螺栓联结预应力施加方法改进研究[J].海军工程大学学报,2010,22(2):20-24.JIN Jing.Bolt joint pre-stress load adding method based on transient analysis[J].Journal of naval university of engineering,2010,22(2):20-24.
